Rabi oscillation

schematic representation of a two-state system that interacts with electromagnetic radiation.

Rabi oscillations occur in a quantum mechanical two-level system (e.g. two states in an atom), which is combined with an external periodic force (e.g. a laser light field in laser spectroscopy or an oscillating magnetic field in nuclear magnetic resonance spectroscopy ) (Circular) frequency interacts. If the excitation frequency is close to the resonance frequency of the two states, the occupation of the states oscillates with a frequency that is also referred to as the Rabi frequency . It is named after the American physicist Isidor Isaac Rabi . ${\displaystyle \omega }$ ${\displaystyle \omega }$ ${\displaystyle \omega _{21}=\Delta E/\hbar =(E_{2}-E_{1})/\hbar }$ ${\displaystyle \Omega }$

Rabi oscillations are especially important for describing the interaction of coherent light with atoms. Under certain simplifying assumptions, two electron states of the atom can be approximated as a two-level system, which is disturbed by the (weak) light field. This allows the properties of the system to be calculated within the framework of its perturbation theory . The increase in the occupation probability of the second (energetically higher) state then corresponds to the absorption of light. Rabi oscillations can be measured experimentally. In many cases, however, damping or dephasing processes play an important role, as a result of which the oscillations quickly subside and (if at all) can only be observed for a very short time.

Resonant interaction

The two states 1 and 2 of the system have the energies and . The associated frequency of the transition is then . If the disturbance is resonant, then the Rabi frequency in the case of atom-light interaction is: ${\displaystyle E_{1}}$ ${\displaystyle E_{2}}$ ${\displaystyle \omega _{21}={\frac {E_{2}-E_{1}}{\hbar }}}$ ${\displaystyle \omega \equiv \omega _{21}}$

${\displaystyle \Omega _{\mathrm {Atom-Licht} }={\frac {{\vec {d}}_{12}\cdot {\vec {E}}_{0}}{\hbar }}.}$

Here is the strength of the incident light field (electric field component, which predominates here), the transition dipole moment of the transition and the reduced Planck's quantum of action. In the case of nuclear magnetic resonance spectroscopy (NMR), an oscillating magnetic field with strength interacts with the magnetic dipole moment of an atom generated by the nuclear spin . The Rabi frequency of this system results from the gyromagnetic ratio to: ${\displaystyle {\vec {E}}_{0}}$ ${\displaystyle {\vec {d}}_{12}}$ ${\displaystyle 1\rightarrow 2}$ ${\displaystyle \hbar }$ ${\displaystyle {\vec {B}}_{1}}$ ${\displaystyle {\vec {I}}}$ ${\displaystyle {\vec {\mu }}=\gamma \,{\vec {I}}}$ ${\displaystyle \gamma }$

${\displaystyle \Omega _{\mathrm {NMR} }=\gamma \,B_{1}.}$

The occupation probabilities and the states oscillate with the Rabi frequency according to the following formula: ${\displaystyle p_{1}(t)}$ ${\displaystyle p_{2}(t)}$ ${\displaystyle \Omega }$

${\displaystyle p_{1}(t)=\cos ^{2}\left({\frac {\Omega \,t}{2}}\right)}$ and ${\displaystyle p_{2}(t)=\sin ^{2}\left({\frac {\Omega \,t}{2}}\right).}$

It was assumed that only basic state 1 was currently occupied. ${\displaystyle t=0}$

Detuned interaction

If, instead of a resonant interference field, a detuned interference field is radiated, the Rabi frequency also changes to: ${\displaystyle \Delta =\omega _{21}-\omega }$

${\displaystyle \Omega '\equiv {\sqrt {\Omega ^{2}+\Delta ^{2}}},}$

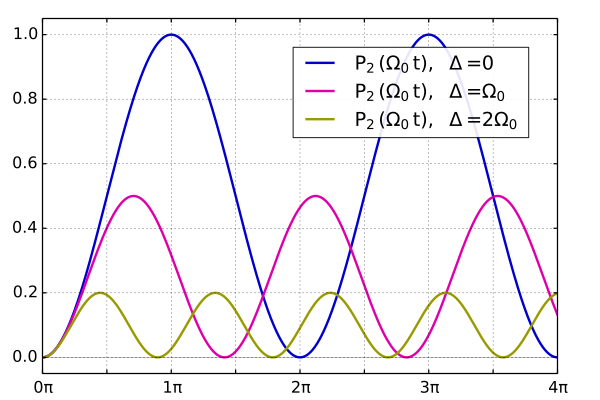
where is the Rabi frequency of the resonantly disturbed system. A complete theoretical treatment is possible with the help of the time-dependent perturbation theory. For the occupation probability of the excited state, the following time course results (at the moment only the ground state 1 was occupied again): ${\displaystyle \Omega }$ ${\displaystyle p_{2}(t)}$ ${\displaystyle t=0}$

${\displaystyle p_{2}(t)={\frac {\Omega ^{2}}{\Omega '^{2}}}\sin ^{2}{\frac {\Omega '\cdot t}{2}}}$

and the occupancy probability for the state is 1 . The line-up is shown in the following picture for various upsets : ${\displaystyle p_{1}(t)=1-p_{2}(t)}$ ${\displaystyle p_{2}(t)}$ ${\displaystyle \Delta }$

Due to the external disturbance, state 2 is occupied up to a maximum value and then released again. This behavior continues periodically. It is noteworthy in this case that a complete implementation is only possible if the detuning is zero, i.e. the frequency of the disturbance hits the transition frequency resonantly. It should also be noted that the Rabi oscillations in this (simplified) model continue for all times and therefore a steady change in occupation of the states is not possible when the disturbance is switched on.

The amplitude of the Rabi oscillations describes the cross-section when the two-level transition is excited. According to the above formula, it is : ${\displaystyle \sigma (\omega )}$ ${\displaystyle p_{2}(t)}$

${\displaystyle \sigma _{\mathrm {21} }(\omega )\propto {\frac {\Omega ^{2}}{{\bigl |}\Omega ^{2}+\left(\omega _{21}-\omega \right)^{2}{\bigr |}}}.}$

This corresponds to a Lorentz curve , which is also typical for other resonance phenomena.

Derivation

The Hamilton operator of the system is divided into two parts:

${\displaystyle {\hat {H}}={\hat {H}}^{(0)}+{\hat {H}}^{(1)}(t)}$, With ${\displaystyle {\hat {H}}^{(1)}(t)=-\hbar \Omega \,\cos(\omega t)(|1\rangle \langle 2|+|2\rangle \langle 1|)}$

where describe the undisturbed two-level system and the time-dependent disturbance. The states already mentioned above are now the solutions of the undisturbed Hamilton operator: ${\displaystyle {\hat {H}}^{(0)}}$ ${\displaystyle {\hat {H}}^{(1)}(t)}$ ${\displaystyle |1\rangle ,|2\rangle }$

${\displaystyle {\hat {H}}^{(0)}|1\rangle =E_{1}|1\rangle }$and . ${\displaystyle {\hat {H}}^{(0)}|2\rangle =E_{2}|2\rangle \quad }$

With these states one can solve the time-dependent Schrödinger equation ${\displaystyle |\Psi (t)\rangle }$

${\displaystyle {\hat {H}}|\Psi (t)\rangle =i\hbar {\frac {\partial }{\partial t}}|\Psi (t)\rangle }$

apply as a linear combination of the undisturbed solutions:

${\displaystyle |\Psi (t)\rangle =c_{1}(t)\,\exp(-iE_{1}t/\hbar )\,|1\rangle +c_{2}(t)\,\exp(-iE_{2}t/\hbar )|2\rangle }$.

Inserting this approach into the time-dependent Schrödinger equation results in a system of two coupled differential equations for and , which has the following solution: ${\displaystyle c_{1}(t)}$ ${\displaystyle c_{2}(t)}$

${\displaystyle c_{1}(t)=\left[\cos \left({\frac {\Omega 't}{2}}\right)+i{\frac {\Delta }{\Omega '}}\,\sin \left({\frac {\Omega 't}{2}}\right)\right]\,e^{-i\Delta \,t/2}}$ and

${\displaystyle c_{2}(t)=i{\frac {\Omega }{\Omega '}}\,\sin \left({\frac {\Omega 't}{2}}\right)\,e^{i\Delta \,t/2}\quad }$,

from which the above occupation probabilities as and result. ${\displaystyle p_{1}(t)=|c_{1}(t)|^{2}}$ ${\displaystyle p_{2}(t)=|c_{2}(t)|^{2}}$

swell

• PW Milonni, JH Eberly: Lasers . Wiley, 1988, ISBN 0-471-62731-3 .
• HJ Metcalf , P. van der Straten: Laser Cooling and Trapping . Springer, 1999, ISBN 0-387-98747-9 , pp. 4-7.
• PW Atkins , RS Friedman: Molecular Quantum Mechanics . 4th ed., Oxford University Press, Oxford 2004, ISBN 0-19-927498-3 .

Web links

• tugraz.at: Double potential well: Example NH ₃ (PDF; 2 MB)
• Light-atom interaction in the two-level system ( Memento from December 20, 2005 in the Internet Archive )