Archimedean spiral

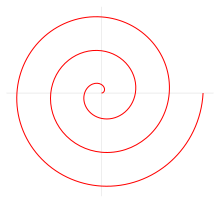
Archimedean spiral in a polar coordinate system

The Archimedean spiral (also arithmetic spiral ) is the simplest of all spirals. It occurs when the radius increases proportionally to the angle of rotation during a rotary movement : ${\ displaystyle r}$ ${\ displaystyle \ varphi}$

{\ displaystyle r = a \ cdot \ varphi}

with . ${\ displaystyle a> 0}$

properties

The representation as a parameter curve in Cartesian coordinates is:

{\ displaystyle f \ colon \ varphi \ mapsto (r \, \ cos \ varphi, r \, \ sin \ varphi) = (a \, \ varphi \, \ cos \ varphi, a \, \ varphi \, \ sin \ varphi)}

.

The length of an arc from to is ${\ displaystyle \ \ varphi _ {1}}$ ${\ displaystyle \ varphi _ {2}}$

{\ displaystyle {\ frac {a} {2}} \ left [\ varphi \, {\ sqrt {1+ \ varphi ^ {2}}} + \ ln \ left (\ varphi + {\ sqrt {1+ \ varphi ^ {2}}} \ right) \ right] _ {\ varphi _ {1}} ^ {\ varphi _ {2}}}

or short:

{\ displaystyle {\ frac {a} {2}} \ left [\ varphi \, {\ sqrt {1+ \ varphi ^ {2}}} + \ operatorname {arsinh} \ varphi \ right] _ {\ varphi _ {1}} ^ {\ varphi _ {2}}}

The total length of the spiral from to is therefore ${\ displaystyle \ varphi _ {1} \ = \ 0}$ ${\ displaystyle \ varphi _ {2} \ = \ \ varphi}$

{\ displaystyle {\ frac {a} {2}} \ left [\ varphi \, {\ sqrt {1+ \ varphi ^ {2}}} + \ ln \ left (\ varphi + {\ sqrt {1+ \ varphi ^ {2}}} \ right) \ right].}

The area included in the first revolution is

{\ displaystyle {\ frac {4} {3}} \ pi ^ {3} a ^ {2},}

while at the n-th revolution the area

{\ displaystyle \ 8 (n-1) \ pi ^ {3} a ^ {2}}

is additionally included.

Archimedean spiral with parameters and pitch

The curvature is calculated as follows depending on the angle of rotation : ${\ displaystyle \ varphi}$

{\ displaystyle \ kappa = {\ frac {\ varphi ^ {2} +2} {a (\ varphi ^ {2} +1) ^ {\ tfrac {3} {2}}}}}

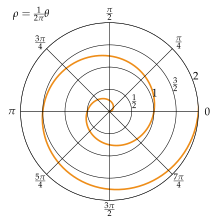
In addition to the above representation as a parameter curve, the Archimedean spiral can also be described as an equation:

{\ displaystyle \ tan \ left ({\ frac {\ sqrt {x ^ {2} + y ^ {2}}} {a}} \ right) = {\ frac {y} {x}}}

"Winding spacing"

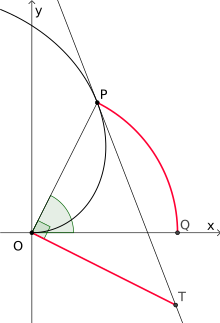
Each ray emanating from the origin (0 | 0) intersects successive turns of the Archimedean spiral in points with the constant distance (see figure on the right!). This is where the term “arithmetic spiral” comes from. ${\ displaystyle \ r = a \, \ varphi \}$ ${\ displaystyle a \ cdot 2 \, \ pi \}$

Tangent to the spiral, the red paths are the same length.

This special property of the Archimedean spiral is often expressed in such a way that its winding spacing is constant. However, this way of speaking can easily be misunderstood, since it is not a question of a constant distance between curves in the sense of parallel curves . A spiral whose turns actually have a constant distance in the latter sense would be the involute of a circle .

Tangent property

A point P is given with the associated radius OP and the angle of rotation . The tangent to the spiral through P then intersects the perpendicular to OP established in O at a point T. Then the circular arc PQ belonging to the angle of rotation is exactly as long as the segment OT, that is, it applies: ${\ displaystyle \ varphi}$ ${\ displaystyle \ varphi}$

{\ displaystyle \ angle POT = 90 ^ {\ circ} \, \ Rightarrow \, | {\ widehat {PQ}} | = | OT |}

Angular division and circle quadrature

Angular division into three (n = 3):

{\ displaystyle \ beta = {\ tfrac {\ alpha} {3}}}

Circle quadrature according to Archimedes

Circle quadrature: F (circle (M, r)) = F (ABCD) = F (CJHG)

Due to its definition, according to which the distance of a curve point from the origin is proportional to the angle of rotation, the Archimedean spiral is suitable for dividing an angle into n equal parts and for squaring the circle . It is therefore both a trisectrix (n = 3) and a quadrix . Both problems can not be solved with a compass and ruler alone, but if the Archimedean spiral is allowed as the only additional aid, they can be solved.

To divide an angle BAC into n equal parts, an Archimedean spiral is first created over its leg AB. The leg functions as the x-axis with the angle tip A as the origin. The distance from the angle tip to the intersection point D of the spiral with the other angle leg is now divided into n parts of equal length. With the help of the theorem of rays this can only be done with a compass and ruler, for this one draws a further ray from the angle tip A and draws off n equal distances from the angle tip with the compass. Then connect the end point of the last segment with the point D and the angle leg and draw parallels to this segment through the n-1 further segment ends on the ray from the angle tip A. The intersection points of the parallels with angle leg AC divide the segment AD into n of equal length Sections. Now you construct n-1 circles that have the angle point A as the center and go through the n-1 end points of the segments of AD. Finally, the n-1 points of intersection of the n-1 circles are connected to the spiral with the angle tip A, thus dividing the angle BAC into n equal angles.

To quadrature a circle with radius r, one first constructs two mutually perpendicular coordinate axes through its center point M and creates an Archimedean spiral in this coordinate system. The spiral intersects the y-axis at a point E and the length of the line ME is units of length, since the corresponding angle of rotation of the spiral is. Then the rectangle with the circle diameter (2r) has as length and | ME | same area as the circle. With the help of Euclid's theorem of heights , the rectangle can then be transformed into a square with the same area. ${\ displaystyle {\ tfrac {r \ pi} {2}}}$ ${\ displaystyle {\ tfrac {\ pi} {2}}}$

Archimedes himself used a different method for quadrature. He first constructed the spiral for one full revolution in a coordinate system with origin O, so that this positive half of the x-axis intersects in P. The tangent of the spiral at point P intersects the y-axis in T and the right-angled triangle OPT has the same area as the circle with center O and radius OP. This triangle can easily be converted into a rectangle of equal area (halving one of the two cathets), which, as above, can be transformed into a square of equal area with the help of Euclid's theorem of heights.

Historical

Archimedes described the spiral named after him in 225 BC. In his treatise “On Spirals” , but it was already known to his friend and contemporary Konon of Samos , who is considered to have discovered it. In the 4th century AD it was examined by Pappos . The general determination of the spiral length was made by Isaac Barrow in 1670.

Generalizations

There are various generalizations of the spiral originally described by Archimedes, for which Archimedean spirals are often used as a collective term in the literature. Here the original equation is extended to with . For you get the usual spiral of Archimedes. The fall is also known as the Fermatian spiral , the fall as the lituus spiral and the fall as the hyperbolic spiral . In general, these spirals can differ significantly from the original Archimedean spiral in terms of properties and appearance. ${\ displaystyle r = a \, \ varphi}$ ${\ displaystyle r = b + a \, \ varphi ^ {\ tfrac {1} {d}}}$ ${\ displaystyle d \ in \ mathbb {R}}$ ${\ displaystyle d = 1, \, b = 0}$ ${\ displaystyle d = 2, \, b = 0}$ ${\ displaystyle d = -2, \, b = 0}$ ${\ displaystyle d = -1, \, b = 0}$

Applications

Liquorice snails in the shape of an Archimedean spiral

Records as an application of Archimedean spirals

Many storage media use at least approximately the principle of the Archimedean spiral, so storage tapes (e.g. audio and video cassettes ) roll up in the form of a spiral. Tracks on records or CDs are also arranged in the form of an Archimedean spiral, this enables the reading head to read any amount of data linearly ( sequentially ) without interrupting a track change .

Hard disk drives for random access , however use since the beginning of blocks / circular segments on concentrically arranged circles .

literature

DDSokolov: Archimedean spiral . In Encyclopaedia of Mathematics , Volume 1, p. 240
Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics . MAA 2010, ISBN 978-0-88385-348-1 , pp. 145-146 ( excerpt (Google) )
Janos Aczel, Claudi Alsina: Trisection of Angles, Classical Curves, and Functional Equations . Mathematics Magazine, Vol. 71, No. 3 (June 1998), pp. 182-189 ( JSTOR 2691201 )
Alexander Ostermann, Gerhard Wanner: Geometry by Its History . Springer, 2012, ISBN 978-3-642-29163-0 , pp. 81-82
Midhat J. Gazalé: Gnomon: From Pharaohs to Fractals . Princeton University Press, 1999, ISBN 978-0-691-00514-0 , pp. 168-171
Martin Gardner: The Unexpected Hanging, and Other Mathematical Diversions . University of Chicago Press, 1969, pp. 103-107

Web links

Commons : Archimedean spiral - collection of images, videos and audio files

Eric W. Weisstein : Archimedean spiral . In: MathWorld (English).
John J. O'Connor, Edmund F. Robertson : Spiral of Archimedes. In: MacTutor History of Mathematics archive .

Individual evidence

↑ ^a ^b JW Rutter: Geometry of Curves . CRC Press, 2000, p. 71
↑ Dietmar Herrmann: The ancient mathematics: A history of Greek mathematics, its problems and solutions . Springer, 2014, ISBN 978-3-642-37612-2 , pp. 181-187
^ JW Rutter: Geometry of Curves . CRC Press, 2000, p. 149
^ ^A ^b Alexander Ostermann, Gerhard Wanner: Geometry by Its History . Springer, 2012, ISBN 978-3-642-29163-0 , pp. 81-82
^ ^A ^b Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics . MAA 2010, ISBN 978-0-88385-348-1 , pp. 145-146 ( excerpt (Google) )
^ Jean-Paul Delahaye: π - The story . Springer, 2013, ISBN 978-3-0348-5085-8 , p. 75

[CRC1-1] JW Rutter: Geometry of Curves . CRC Press, 2000, p. 71

[Herrmann-2] Dietmar Herrmann: The ancient mathematics: A history of Greek mathematics, its problems and solutions . Springer, 2014, ISBN 978-3-642-37612-2 , pp. 181-187

[CRC2-3] JW Rutter: Geometry of Curves . CRC Press, 2000, p. 149

[Wanner-4] A ^b Alexander Ostermann, Gerhard Wanner: Geometry by Its History . Springer, 2012, ISBN 978-3-642-29163-0 , pp. 81-82

[Alsina-5] A ^b Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics . MAA 2010, ISBN 978-0-88385-348-1 , pp. 145-146 ( excerpt (Google) )

[Delahaye-6] Jean-Paul Delahaye: π - The story . Springer, 2013, ISBN 978-3-0348-5085-8 , p. 75