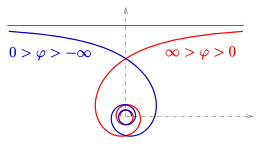
Hyperbolic spiral

Hyperbolic spiral: branch for ${\displaystyle \varphi >0}$

Hyperbolic spiral: both branches

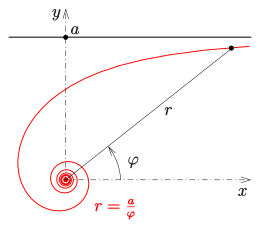
A hyperbolic spiral is a plane curve that is polarized by the equation

${\displaystyle r={\frac {a}{\varphi }}}$

a hyperbola can be described. Since it can also be understood as an inversion (mirroring of a circle) of an Archimedean spiral , the curve is also called a reciprocal spiral .

In 1704 Pierre Varignon studied this curve. Even Johann Bernoulli and Roger Cotes dealt later with it.

Description in Cartesian coordinates

The hyperbolic spiral with the polar equation

${\displaystyle r={\frac {a}{\varphi }}\ ,\quad \varphi \neq 0}$

can be in Cartesian coordinates through the parametric representation ${\displaystyle (x=r\cos \varphi ,\;y=r\sin \varphi )}$

• ${\displaystyle x=a{\frac {\cos \varphi }{\varphi }},\qquad y=a{\frac {\sin \varphi }{\varphi }},\quad \varphi \neq 0}$

describe.

The hyperbola in the - plane has the coordinate axes as asymptotes. The hyperbolic spiral (in the - plane) approaches the zero point. There is an asymptote for (see next section). ${\displaystyle r}$ ${\displaystyle \varphi }$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle \varphi \to \pm \infty }$ ${\displaystyle \varphi \to \pm 0}$

The parameter representation and results in a representation with an equation : ${\displaystyle \ \varphi ={\frac {a}{r}},\ r={\sqrt {x^{2}+y^{2}}}\ }$

• ${\displaystyle {\frac {y}{x}}=\tan {\big (}{\frac {a}{\sqrt {x^{2}+y^{2}}}}{\big )}\ .}$

properties

asymptote

Because of

${\displaystyle \lim _{\varphi \to 0}x=a\lim _{\varphi \to 0}{\frac {\cos \varphi }{\varphi }}=\infty ,\qquad \lim _{\varphi \to 0}y=a\lim _{\varphi \to 0}{\frac {\sin \varphi }{\varphi }}=a\cdot 1=a}$

the curve has one

• Asymptote with the equation ${\displaystyle \ y=a.}$

curvature

With the formula

${\displaystyle \kappa ={\frac {r^{2}+2(r')^{2}-r\;r''}{(r^{2}+(r')^{2})^{3/2}}}}$

for the curvature of a curve in polar representation and the derivatives and the hyperbolic spiral results for the curvature ${\displaystyle \;r=r(\varphi )\;}$ ${\displaystyle \;r'={\tfrac {-a}{\varphi ^{2}}}\;}$ ${\displaystyle \;r''={\tfrac {2a}{\varphi ^{3}}}\;}$

• ${\displaystyle \kappa (\varphi )={\frac {\varphi ^{4}}{a(\varphi ^{2}+1)^{3/2}}}.}$

Inversion of an Archimedean spiral

Hyperbolic spiral (blue) as an image of an Archimedean spiral (green) when reflected on the unit circle (red)

The reflection on the unit circle (inversion) can be described in polar coordinates by . ${\displaystyle \ (r,\varphi )\to ({\tfrac {1}{r}},\varphi )\ }$

• The image of the Archimedean spiral with is the hyperbolic spiral with the equation when it is reflected on the unit circle ${\displaystyle \;r={\tfrac {\varphi }{a}}\;}$ ${\displaystyle \;r={\tfrac {a}{\varphi }}\;.}$

For both curves intersect at a fixed point on the unit circle. ${\displaystyle \varphi =a}$

The circle of curvature of the Archimedean spiral at the zero point has the radius (see curvature of the Archimedean spiral ) and the center . This circle merges into a straight line when the circle is mirrored (see inversion ). So: ${\displaystyle \;r={\tfrac {\varphi }{a}}\;}$ ${\displaystyle \rho _{0}={\tfrac {1}{2a}}}$ ${\displaystyle (0,\rho _{0})}$ ${\displaystyle y=a}$

• The prototype of the asymptote of the hyperbolic spiral in the mirroring of the Archimedean spiral is the circle of curvature of the Archimedean spiral at the zero point.

example

The picture shows an example with . The curve of the Archimedean spiral (green) that lies in the unit circle (red) is mapped onto the part of the hyperbolic spiral (blue) that lies outside the circle. ${\displaystyle a=\pi }$

Arc length

The length of the arc of a hyperbolic spiral between two points can be calculated using the formula for curves in polar representation : ${\displaystyle \;(r(\varphi _{1}),\varphi _{1}),(r(\varphi _{2}),\varphi _{2})\;}$

${\displaystyle L=\int \limits _{\varphi _{1}}^{\varphi _{2}}{\sqrt {\left(r^{\prime }(\varphi )\right)^{2}+r^{2}(\varphi )}}\,\mathrm {d} \varphi =\cdots =a\int \limits _{\varphi _{1}}^{\varphi _{2}}{\frac {\sqrt {1+\varphi ^{2}}}{\varphi ^{2}}}\,\mathrm {d} \varphi }$

${\displaystyle \qquad =a{\Big [}-{\frac {\sqrt {1+\varphi ^{2}}}{\varphi }}+\ln(\varphi +{\sqrt {1+\varphi ^{2}}}){\Big ]}_{\varphi _{1}}^{\varphi _{2}}\ .}$

Hyperbolic spiral: sector

Sector area

The area of ​​a sector of the hyperbolic spiral is calculated in polar coordinates:

${\displaystyle A={\tfrac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}r(\varphi )^{2}\;d\varphi ={\tfrac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}{\frac {a^{2}}{\varphi ^{2}}}\;d\varphi ={\frac {a}{2}}{\big (}{\frac {a}{\varphi _{1}}}-{\frac {a}{\varphi _{2}}}{\big )}}$

${\displaystyle \quad ={\frac {a}{2}}{\big (}r(\varphi _{1})-r(\varphi _{2}){\big )}\ .}$

Central projection of a helix

The central projection of a helix is ​​a hyperbolic spiral if the main point and eye point lie on the helix axis, see helix (descriptive geometry) .

literature

• IN Bronstein, KA Semendjajew: Taschebuch der Mathematik , Harri Deutsch Verlag, 1983, ISBN 3871444928 , p. 146.
• Hans-Jochen Bartsch, Michael Sachs: Paperback mathematical formulas for engineers and natural scientists , Carl Hanser Verlag, 2018, ISBN 3446457070 , 9783446457072, p. 410.
• Kinko Tsuji, Stefan C. Müller: Spirals and Vortices: In Culture, Nature, and Science , Springer, 2019, ISBN 3030057984 , 9783030057985, p. 96.
• Pierre Varignon: Nouvelle formation de Spirales - exemple II , Mémoires de l'Académie des sciences de l'Institut de France, 1704, pp. 94-103.
• Friedrich Grelle : Analytical Geometry of the Plane , Verlag F. Brecke, 1861 hyperbolic spiral , p. 215.
• Jakob Philipp Kulik : Textbook of higher analysis, Volume 2 , In Commiss. at Kronberger u. Rziwnatz, 1844, Spirallinien , p. 222.

Individual evidence

1. ^ John J. O'Connor, Edmund F. Robertson :  Hyperbolic Spiral. In: MacTutor History of Mathematics archive .

Web links

• Eric W. Weisstein : Hyperbolic Spiral . In: MathWorld (English).
• Online exploration using JSXGraph (JavaScript)