Helix (descriptive geometry)

The articles helix (descriptive geometry) and helix overlap thematically. Help me to better differentiate or merge the articles (→  instructions ) . To do this, take part in the relevant redundancy discussion . Please remove this module only after the redundancy has been completely processed and do not forget to include the relevant entry on the redundancy discussion page{{ Done | 1 = ~~~~}}to mark. Minderbinder 13:37, 12 Aug 2019 (CEST)

Helix:
left or right

Helix:
thread wound around a cylinder

A helix , and the helical line or helix called, is in the geometry of a curve in 3-dimensional space formed by a combination of rotation (rotation) and displacement occurs (translation) along the axis of rotation. Helix lines play an important role in descriptive geometry when depicting spiral staircases , threads and twist drills .

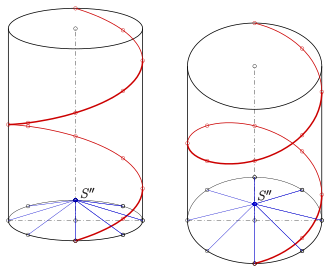
A helix is ​​a simple, mathematically and technically interesting spatial curve. There are also ellipses in space, but they are always flat curves. Screw lines can be easily created with the help of a tightly stretched thread between two cylinder points (see picture). That is, they are the shortest connections between two points on a cylinder. This can also be seen in the particularly simple development of a helix: the development of a helix is ​​a straight line.

Note:

1. This article does not deal with the properties and occurrences of helical lines (see the article Helix ), but shows how to construct projections of helical lines with the means of descriptive geometry ( compasses and rulers ).
2. In books on descriptive geometry, the term is often helix (similar to screw surface ) is used as opposed to the usual designation screw s line .

Parameter representation and names

A helix can be imagined as a curve on a perpendicular circular cylinder , which has the same slope at every point in relation to the plane of the base circle. If the cylinder axis is the axis and the curve begins at the point , the helix can be shown through the parameter representation ${\displaystyle z}$ ${\displaystyle (r,0,0)}$

• ${\displaystyle (r\cos t,r\sin t,ct)\ ,\ c\neq 0}$

describe. Here is the radius of the cylinder and the screw parameters . ${\displaystyle r}$ ${\displaystyle c}$

The helix is ​​called right-handed , ${\displaystyle c>0}$

for left-hand . ${\displaystyle c<0}$

(For the curve is a circle.) ${\displaystyle c=0}$

Tangents of a helix

The height difference that a curve point overcomes by changing the parameter by is ${\displaystyle t}$ ${\displaystyle 2\;\pi }$

• the pitch . ${\displaystyle h=c2\pi }$
• The slope (the tangent of the slope angle ) of the curve (i.e. the tangent) with respect to the - plane is constant . It follows that ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle c/r}$
• the development of the curve is a straight line of the slope . ${\displaystyle c/r}$

This property can be reversed to a helix as on development of a straight line on a cylinder shell manufacture (see Fig.).

• Every geodetic (shortest connection of two points) on the cylinder is a helix.

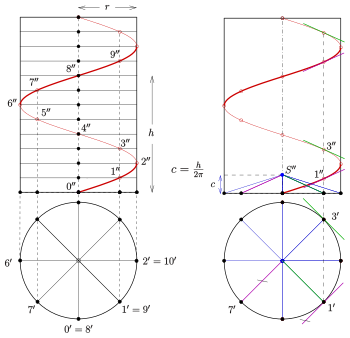
Floor plan, elevation and tangents

The ground plan and elevation of a screw line, the axis of which is perpendicular to the ground plan, can be easily created:

Given : the radius of the associated cylinder, the pitch and the point of the helix on the base circle of the cylinder. ${\displaystyle r}$ ${\displaystyle h}$ ${\displaystyle P_{0}}$

Helix: point construction in plan and elevation, tangent construction (right)

The plan of the helix is ​​the base circle of the cylinder on which the helix lies (important for the tangent construction).

In order to determine the elevation e of a series of points on the helix, one selects pairs of points from the base circle so that they lie on a diameter and adjacent points have an angular distance of (as in the picture) or or . The angular distance should always be chosen so that for each pair of points on a diameter there is also the pair of points on the associated orthogonal diameter. ${\displaystyle P_{0},P_{1},\dotsc ,P_{n}}$ ${\displaystyle 45^{\circ }}$ ${\displaystyle 30^{\circ }}$ ${\displaystyle 15^{\circ }}$

Now draw the pitch on the cylinder axis in the elevation , divide this section into equal parts and draw in the corresponding contour line. The intersection of the folder at point with the -th contour line provides the elevation of the point . If more than one turn is to be drawn, the procedure is continued upwards (see picture). ${\displaystyle h}$ ${\displaystyle n}$ ${\displaystyle P_{i}}$ ${\displaystyle i}$ ${\displaystyle P_{i}}$

Tangent construction: The floor plan of the tangent at a point on the helix is ​​simply the associated tangent to the floor plan circle (see right picture). To determine the elevation of the tangents, select a point on the cylinder axis and move all tangents to this point. The tangents are then generators of a cone with a tip . If the height , all tangents meet the base circle at one of the selected points. The cone thus generated from all tangents of the helix is called a directional cone . ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle c={\tfrac {h}{2\pi }}}$

For example: The outline of the tangent at the point (purple) is parallel to the associated generating line of the directional cone. The same applies to the outline of the tangent at the point (green). ${\displaystyle P_{1}}$ ${\displaystyle P_{3}}$

Well characterized one freehand or with the aid of a curve ruler a curve through the elevation points which contacts the tangents constructed.

Based on the parameter representation or the picture (floor plan and elevation) you can see:

• The elevation of the helix is ​​a sine curve .

Orthogonal parallel projection

Construction of an orthogonal parallel projection of a helix

To produce a more general orthogonal projection, the cylinder including the helix can be tilted by an angle around a diameter of the base circle. ${\displaystyle \delta }$

1. For the new crack (O-crack), choose the position of the center of the base circle and represent the tilted cylinder in a side elevation along with the height markings of the points to be drawn.
2. The base circle appears in the O-crack as an ellipse, the major semi-axis of which is the circle radius. In the side view, the base circle appears as a segment (purple), the end points of which supply the missing vertices of the ellipse in the O-crack via folders. This clearly defines the ellipse and can be drawn using one of the available methods (see Drawing ellipses ). Since the ellipse is not part of the projection of the helical line to be drawn, it is sufficient to draw the 8 ground plan points, but exactly, using the de-la-Hire method or the side plan (folding the base circle into the illustration).
3. If you turn the base circle (ellipse) in the O-crack into the picture table, the base circle appears in its true form and the ground plans of the points to be drawn (1, 2, ..., 12) of the screw lines can be drawn. Turning back the circle provides the plan points in the O-crack (on the ellipse).
4. In order to be able to mark a point of the screw line in the O-crack, you need the height shortened by the tilting (red) above the respective ground plan point (in the picture: construction of the point ). ${\displaystyle P_{9}}$
5. The respective tangents can be drawn in with the aid of the directional cone, as with the floor plan and elevation.
6. After constructing the helix points including tangents in the O-crack, the helix can be drawn freehand or with the help of a curve ruler.

More examples of orthogonal projections

More examples of orthogonal projections

If you tilt the cylinder so far that the projection of the tip of the directional cone lies on the image of the base circle, the orthogonal projection of a helical line has a tip. In this case the projection rays are parallel to a tangent of the helix. If you tilt it further, the image of the helix becomes a loop. One calculates:

• The orthogonal projection of a helical line is the affine image of a possibly lengthened or shortened cycloid .

Inclined parallel projection: bird's eye view

Bird's eye view

A bird's eye view (military projection), in which the picture panel is the base circle plane of the cylinder, can be produced more easily because the base circle remains fixed. So there is no need to construct an ellipse here. The price for this is the poorer image effect.

1. First you draw the base circle and the (here 8) ground plans of the 12 points of the screw line to be drawn.
2. One draws a side plan assigned to the floor plan and plots the heights of the points on the cylinder axis. ${\displaystyle P_{0},\dotsc ,P_{12}}$
3. The oblique projection direction is determined by the angle . ${\displaystyle \beta }$
4. In the drawing, the axis point is projected onto the floor plan and the determined height of (red) is plotted in the table (floor plan) above the associated floor plan point. ${\displaystyle A_{9}}$ ${\displaystyle P_{9}}$
5. The tangents can be determined with the help of the directional cone, analogous to the ground plan and elevation.
6. Draw the curve.

Floor plan, elevation and orthogonal parallel projection of a spiral staircase

Spiral staircase

For a spiral staircase, you screw a specified 1st step. Each point moves on a helical line. Floor plan, elevation and the orthogonal parallel projection can be constructed using the methods described here.

Central projection

Illustration parallel to the screw axis

Central projection of a screw line in architect's arrangement

For a central projection of a helix using the architect arrangement, the following requirements are made in this section:

1. The axis of the helix is vertical . It is given in a simplified elevation through its floor plan and the heights of the points to be drawn on the cylinder axis.
2. The table is vertical and includes the cylinder axis for the sake of simplicity. It is given in the floor plan together with the eye point . The elevation (right) shows the cylinder axis with the height information of the points to be drawn and the elevation of the horizon . ${\displaystyle \pi }$ ${\displaystyle O}$ ${\displaystyle h}$
3. First, the horizon (parallel to ), the main point , the vanishing points of the inclined circle diameter and, with the help of the outline (right), the cylinder axis with the height points are drawn in the picture (above the floor plan). ${\displaystyle h}$ ${\displaystyle h'}$ ${\displaystyle H}$ ${\displaystyle F_{1},F_{2}}$ ${\displaystyle A_{0},A_{1},\dotsc }$
4. Determining (in the image): In the plan view of the floor plan is from on the floor plan projected image panel and located (top) of the associated folder in the image. Since the perpendicular to the picture board lies through , the intersection of this perpendicular (straight line ) with the folder drawn is the image you are looking for ( labeled with ) of the point . ${\displaystyle P_{0}}$ ${\displaystyle 0'}$ ${\displaystyle P_{0}}$ ${\displaystyle \pi '}$ ${\displaystyle P_{0}}$ ${\displaystyle A_{0}}$ ${\displaystyle HA_{0}}$ ${\displaystyle 0}$ ${\displaystyle P_{0}}$
5. The image of the point lies on the associated folder and the straight line . ${\displaystyle P_{1}}$ ${\displaystyle F_{1}A_{1}}$
6. Since the picture is on the horizon, the folder with the horizon is cut here. ${\displaystyle P_{2}}$
7. ${\displaystyle P_{3},\dotsc ,P_{8}}$ analogous.
8. Since the construction of the respective tangent is too complex, it is omitted here and the curve is drawn freehand or with a curve ruler. The number of points can be increased to improve the result.

Central projection of a staircase with a vertical picture panel

Example: spiral staircase

The picture shows the central projection of a spiral staircase with a vertical picture table (parallel to the screw axis). The main point is . The steps and helical lines can be constructed with the architect arrangement shown here. ${\displaystyle H}$

Illustration perpendicular to the screw axis

Central projection of a helix as a hyperbolic spiral

Central projection of a spiral staircase, H and O on the axis

Hyperbolic spiral when looking through a spiral staircase

In this case it is assumed that the principal point and the eye point lie on the cylinder axis. In order to be able to draw the picture with the help of an architect arrangement with a vertical picture board, it is assumed that the above elevation of a screw line (sine curve) is used here as a floor plan. For technical reasons of drawing, the eye point is placed at a certain distance in front of the center point of the front circle of the lid and the panel cuts the cylinder in a purple circle (see picture). This circle is shown undistorted. The front circle appears as an enlarged circle, the back circle appears as a smaller one. In this case, the straight cylinder lines are mapped onto one another in dividing straight lines (contour lines). The construction of individual pixels of the helix is ​​carried out as in the previous example. In order to determine the asymptote of the resulting hyperbolic spiral, one constructs the trace point and the vanishing point of the tangent in the vanishing point . The image of the horizontal tangent appears in the image as a vertical straight line. ${\displaystyle H}$ ${\displaystyle O}$ ${\displaystyle H}$ ${\displaystyle 14}$

Proof that the image curve is a hyperbolic spiral:

Assumption: The cylinder axis is the axis, the main point and the eye point , where the distance (the distance between the eye point and the main point) is. In this case a point is mapped onto the point (see central projection ). ${\displaystyle z}$ ${\displaystyle H=(0,0,0)}$ ${\displaystyle O=(0,0,d)}$ ${\displaystyle d}$ ${\displaystyle (x,y,z)^{T}}$ ${\displaystyle \;{\tfrac {d}{d-z}}(x,y)\;}$

The image of the helix is the curve . The polar representation of this curve is ${\displaystyle (r\cos t,r\sin t,ct)^{T}}$ ${\displaystyle \;{\tfrac {dr}{d-ct}}(\cos t,\sin t)\;}$

${\displaystyle \rho ={\frac {dr}{d-ct}}\;.}$

This equation describes a hyperbolic spiral , since it represents a hyperbola in the - plane. ${\displaystyle \rho }$ ${\displaystyle t}$

For the parameter , the polar representation has a pole and the helix intersects the vanishing plane (the plane parallel to the image table through the eye point). Only the part of the curve with lies in front of the disappearance plane and is visible. ${\displaystyle t_{0}=d/c}$ ${\displaystyle t<t_{0}}$

The picture of the helix (spiral) has the straight line with the equation

${\displaystyle \sin(t_{0})x-\cos(t_{0})y=t_{0}r}$

as an asymptote. The proof is obtained by calculating the distance of a curve point from the straight line and the limit value thereof for taking into account the addition theorem for sine and the limit value . ${\displaystyle t\to t_{0}}$ ${\displaystyle \lim _{x\to 0}{\tfrac {\sin x}{x}}=1}$

The asymptote of the spiral is the image of the tangent at the point of vanishing of the helix.

The branch of the spiral with (not shown here) is the image of the part of the helix that lies behind the level of disappearance and is therefore invisible. ${\displaystyle t>t_{0}}$

Spiral curves always arise when the image panel is not parallel to the cylinder axis.

See also

• Screw surface
• Helical surface

literature

• U. Graf , M. Barner : Descriptive Geometry. Quelle & Meyer, Heidelberg 1961, ISBN 3-494-00488-9 , pp. 184, 220.
• C. Leopold: Geometric Basics of Architectural Representation. Verlag W. Kohlhammer, Stuttgart 2005, ISBN 3-17-018489-X , p. 125.

Web links

• K. Strubecker: Lectures on descriptive geometry. (PDF; 13 MB), TH Karlsruhe, p. 274.

supporting documents

1. ^ Graf, Barner
2. ↑ Strubecker