Screw surface

Screw surface: parabola is meridian

A screw surface is a surface in geometry that is created by screwing a curve in Euclidean space. If the curve lies in one plane with the screw axis, it is called the meridian . The simplest screw surfaces are the helical surfaces . They are created by screwing a straight line that intersects the screw axis perpendicularly. Important types of screw surfaces are

Standard screw surfaces or jet screw surfaces . They are created by screwing a straight line and are therefore ruled surfaces .

Circular screw surfaces or cyclic screw surfaces . They are created by screwing a circle together .

Helical surfaces play an important role in mathematics (see minimal surface ). Both types play a role in technology (stairs, slides, screws, pipes).

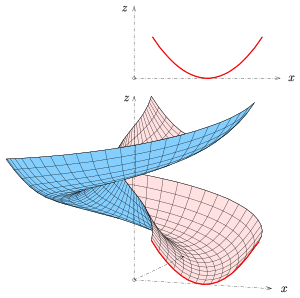
Other profiles (parabola, trapezoid, ...) are also important for technical applications.

Analytical description

Screw connection of a point
green: pitch,
blue: screw axis

Screw connection of a point

The screwing of a point can be imagined as a superposition of a rotation and a shift in the direction of the axis of rotation proportional to the angle of rotation.

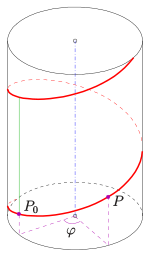
The screwing of the point around the z-axis can be passed through ${\ displaystyle P_ {0} = (x_ {0}, y_ {0}, z_ {0})}$

${\ displaystyle \ mathbf {p} (\ varphi) = {\ begin {pmatrix} x_ {0} \ cos \ varphi -y_ {0} \ sin \ varphi \\ x_ {0} \ sin \ varphi + y_ {0 } \ cos \ varphi \\ z_ {0} + c \; \ varphi \ end {pmatrix}} \, \ \ varphi \ in \ mathbb {R} \,}$

describe. Here, the screw parameters , the angle , measured in radians, the helix angle and the pitch (green). The path of the point is a helix (red). It lies on a straight cylinder, the radius of which is equal to the distance between the point and the screw axis. ${\ displaystyle c \ neq 0}$ ${\ displaystyle \ varphi}$ ${\ displaystyle h = c \; 2 \ pi}$

If is, the resulting helix is called right-handed, otherwise left-handed . (For would result in a rotation around the z-axis). ${\ displaystyle c> 0}$ ${\ displaystyle c = 0}$

Screwing a curve

The screwing of the curve

${\ displaystyle \ mathbf {x} (t) = (x (t), y (t), z (t)) ^ {T}, \ t_ {1} \ leq t \ leq t_ {2} \,}$

supplies the screw surface with the parameter representation

${\ displaystyle \ mathbf {S} (t, \ varphi) = {\ begin {pmatrix} x (t) \ cos \ varphi -y (t) \ sin \ varphi \\ x (t) \ sin \ varphi + y (t) \ cos \ varphi \\ z (t) + c \; \ varphi \ end {pmatrix}} \, \ quad t_ {1} \ leq t \ leq t_ {2}, \ \ varphi \ in \ mathbb {R} \.}$

The surface curves are helical lines. The surface curves are copies of the given curve. ${\ displaystyle \ mathbf {S} (t = const, \ varphi)}$
${\ displaystyle \ mathbf {S} (t, \ varphi = const)}$

Standard screw surfaces

Helical surfaces: closed (left) and open (right)

inclined screw surfaces: closed (left) and open (right)

Screw gate: definition (left) and example

Types

If the given curve is a straight line, a standard screw surface is created. There are 4 cases to be distinguished:

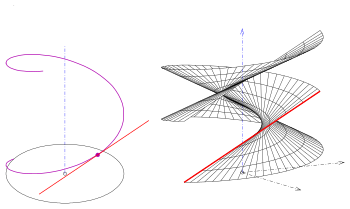
(1) The straight line intersects the screw axis perpendicularly. A helical surface is created (closed straight screw surface ).

(2) The straight line intersects the axis, but not perpendicular. The result is an inclined, closed or sharp screwing surface .

If the straight line is skewed to the screw axis, an open standard screw surface is created . In contrast to the closed standard screw surface, the screw axis does not belong to the surface in this case. The surface points have at least the distance of the starting line from the axis.

(3) If the straight line is crooked in a plane perpendicular to the axis, a straight open screw surface or short open helical surface is created .

(4) If the straight line is crooked and not contained in a plane perpendicular to the axis, an inclined open standard screw surface is created .

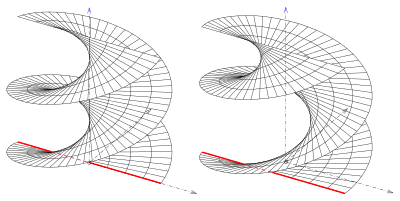
Inclined standard screw surfaces penetrate one another (see picture), straight ones (helical surfaces) do not.

An interesting special case of the inclined open standard screw surfaces is when the screwed straight line has the distance from the screw axis and the angle of inclination with respect to the xy plane . In this case the area can be understood as a torse . It is the tangent surface of the helix (guide curve) , i.e. That is, it is the union of all tangents of the helix. As Torse this Regelschraubfläche is unwound . ${\ displaystyle d}$ ${\ displaystyle \ alpha}$ ${\ displaystyle \ tan \ alpha = c / d}$ ${\ displaystyle (d \ cos \ varphi, d \ sin \ varphi, c \ varphi)}$

Comment:

The helical surfaces are Catalan surfaces . The closed helical surface is even a straight conoid .

Jet screw surfaces are not algebraic surfaces ; that is, they cannot be implicitly described with an algebraic equation. This is made plausible by the fact that there is always a straight line parallel to the screw axis that intersects the surface at an infinite number of points, although it does not belong to the surface.

Via closed regulating screw surfaces

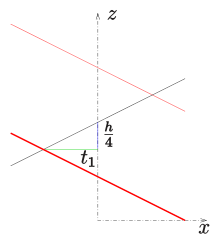
For penetration of closed standard screw surfaces

In the case of a closed standard screw surface, the straight line intersects the screw axis. If the straight line to be screwed is described by , the parameter representation results ${\ displaystyle (t, 0, z_ {0} + m \; t) ^ {T}}$

{\ displaystyle \ mathbf {S} (t, \ varphi) = {\ begin {pmatrix} t \ cos \ varphi \\ t \ sin \ varphi \\ z_ {0} + mt + c \ varphi \ end {pmatrix} } \.}

If is (closed helical surface), the surface does not penetrate itself. If is (inclined closed helical screw surface) , the surface curves are ${\ displaystyle m = 0}$
${\ displaystyle m \ neq 0}$

${\ displaystyle \ mathbf {S} (t_ {i}, \ varphi)}$ with self-penetrating curves (double curves) . ${\ displaystyle t_ {i} = {\ frac {h} {4m}} (2i + 1), \ i = 1,2, \ ldots}$

This is an infinite number of helical lines. The smaller is, the further apart the double curves are. ${\ displaystyle | m |}$

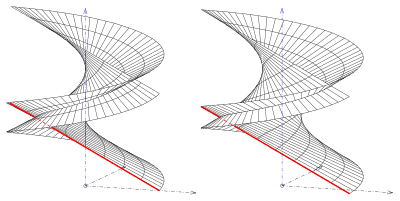
About the screw gate

Screw gate: regular parts (green and blue) and ridge line (purple)

If you go from the helix

{\ displaystyle \ mathbf {x} (\ varphi) = (r \ cos \ varphi, r \ sin \ varphi, c \ varphi) ^ {T}}

off, the corresponding screw gate has the parameter representation:

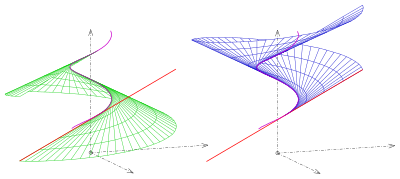
${\ displaystyle \ mathbf {S} (t, \ varphi) = \ mathbf {x} (\ varphi) + t \ mathbf {\ dot {x}} (\ varphi) = {\ begin {pmatrix} r \ cos \ varphi -tr \ sin \ varphi \\ r \ sin \ varphi + tr \ cos \ varphi \\ c (t + \ varphi) \ end {pmatrix}} \.}$

For the surface normal results

${\ displaystyle \ mathbf {n} = \ mathbf {S} _ {t} \ times \ mathbf {S} _ {\ varphi} = \ mathbf {\ dot {x}} \ times (\ mathbf {\ dot {x }} + t \ mathbf {\ ddot {x}}) = t (\ mathbf {\ dot {x}} \ times \ mathbf {\ ddot {x}}) = t {\ begin {pmatrix} cr \ sin \ varphi \\ - cr \ cos \ varphi \\ r ^ {2} \ end {pmatrix}} \.}$

For the normal vector is the zero vector, i. That is, the starting curve (helix) consists of the singular points of the surface. The starting curve is called the ridge line of the screw gate. The ridge line divides the surface into two regular partial surfaces (see picture). ${\ displaystyle t = 0}$

Circular screw surfaces

Meridian circle screw surface

Circle screw surface: screw connection of a horizontal circle

There are 3 interesting types of circular screw surfaces:

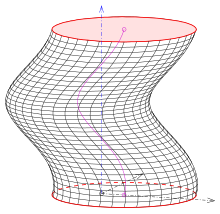
(1) If the circle is a meridian and does not intersect the screw axis, a meridian circle screw surface is created (see picture).

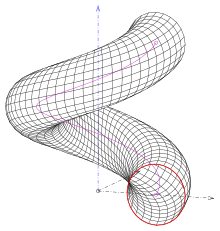
(2) If the circular plane is perpendicular to the helix of the center of the circle, a pipe surface is created . A tube surface is also the envelope of spheres with the same radius, the centers of which are the bolted circle centers.

(3) If the circle is horizontal (in a plane perpendicular to the screw axis) and includes the screw axis, a columnar, straight circular screw surface is created (see picture). It was often used in baroque columns.

Uni-Mannheim new rescue ladder building
Salinarium slide
Pulpit altar (1688), St. Pankratius, Neuenfelde, Germany

Web links

literature

Ulrich Graf, Martin Barner: Descriptive Geometry. Quelle & Meyer, Heidelberg 1961, ISBN 3-494-00488-9 , p. 218.
Karl Strubecker: Lectures on descriptive geometry. Vandenhoeck & Ruprecht, Göttingen 1967, p. 286.