Sliding surface
A sliding surface or translation surface is a surface in geometry that is created by a special type:
- If there are two space curves with a common point , the curve is shifted so that the point slides on the curve . The area swept by is called the sliding area .
If the two curves lie in a common plane, the sliding surface is flat. This case is always excluded here.

Simple examples are
- a perpendicular circle cylinder : is a circle (or another cross-section) and a straight line.
- the elliptical paraboloid : where ( parabola ) and (parabola) are.
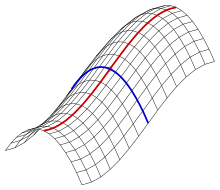
- the hyperbolic paraboloid : where (parabola) and (parabola open downwards) are.
Sliding surfaces play a role in the representational geometry and architecture as easily modelable surfaces.
In differential geometry , minimal surfaces and chord center surfaces are understood and examined as sliding surfaces .
The translation surfaces (sliding surfaces) described here should not be confused with the translation surfaces in the complex geometry .
Parametric representation
If and two space curves are included, the associated sliding surface has the parameter display :
and goes through the zero point. Obviously, the roles of the curves and when creating (sliding) can be reversed. That is why both curves are called sliding curves . A (congruent) curve that has been shifted to and from goes through each point of the surface . The tangential plane in is spanned by the two tangent vectors of the sliding curves if the vectors are linearly independent .
If the condition is not met, the sliding surface defined by (*) does not have to contain the zero point or the curves . The surface always contains shifted images of the curves as parameter curves or .
The representation has the corresponding chord center area
Helical surface as a sliding surface and chord center surface
A helical surface is a special screw surface in which a straight line that intersects the screw axis perpendicularly is screwed. It is an example of a minimal area and can be represented as a sliding area:
The helical surface with the parametric representation
has the pitch . If you introduce new parameters in such a way that
and is a positive number, the new parametric representation is obtained
This is the parameter display of a sliding surface with the two identical sliding curves
- and
The common point used for construction in the drawing is . The (identical) curves are sliding Schraublinien with the pitch on the cylinder with the equation are. All parameter lines are shifted images of the shift curve (purple in the picture). They lie on vertical circular cylinders with a radius that contain the z-axis as the surface line.
The new parametric representation only describes points on the helical surface that lie within the cylinder with the equation .
The new parametric representation of the helical surface also shows that the helical surface can be represented as a chord center surface :
-
- in which
- and
are two identical generator curves.
In the drawing lies on the helix and on the (identical) helix . The middle of the tendon is .
Practical advantages of a sliding surface
- in architecture
A surface (e.g. roof) can easily be created by making a template for the curve and several identical templates for the curve . The stencils can be made without mathematics with artistic freedom. When positioning the templates, you only have to make sure that they are attached according to the principle of the sliding surface.
- in descriptive geometry
To create a parallel projection of a sliding surface, 1) projections of the sliding curves must be produced, 2) a template must be made of the projection of the curve and 3) specimens displaced using this template must be drawn in according to the instructions for the sliding surface. The outline of the surface is the envelope curve of the curves drawn with the template. This applies to both vertical and inclined parallel projections ( cavalier's perspective, bird's eye view ), but not to central projections.
- in differential geometry
Due to the simple formal description of a sliding surface, the partial derivatives of are simple derivatives of the two curves. In particular, mixed partial derivatives are always the same . So when a surface is represented as a sliding surface, the coefficient of the second fundamental form is always the same . This facilitates z. B. the demonstration that a helical surface is a minimal surface (i.e. the mean curvature is ).
literature
- Georg Glaeser: Geometry and its applications in art, nature and technology. Springer-Verlag, 2014, ISBN 978-3-642-41852-5 , p. 259.
- W. Haack: Elementary differential geometry. Springer-Verlag, 2013, ISBN 978-3-0348-6950-8 , p. 140.
- C. Leopold: Geometric Basics of Architectural Representation. Verlag W. Kohlhammer, Stuttgart 2005, ISBN 3-17-018489-X , p. 122.
Individual evidence
- ↑ H. Brauner: Textbook of constructive geometry. Springer-Verlag, 2013, ISBN 978-3-7091-8778-4 , p. 236.
- ↑ Fritz Hohenberg: Constructive geometry in technology. Springer-Verlag, 2013, ISBN 978-3-7091-8148-5 , p. 208.
- ^ Hans Schober: Transparent shells: form, topology, supporting structure. John Wiley & Sons, 2015, ISBN 978-3-433-60598-1 , p. 74.
- ^ Wilhelm Blaschke, Kurt Reidemeister: Lectures on differential geometry and geometrical foundations of Einstein's theory of relativity II: Affine differential geometry. Springer-Verlag, 2013, ISBN 978-3-642-47392-0 , p. 94.
- ↑ Erwin Kruppa: Analytical and constructive differential geometry. Springer-Verlag, 2013, ISBN 978-3-7091-7867-6 , p. 45.
- ↑ JCC Nitsche: Lectures on minimal areas. Springer-Verlag, 2013, ISBN 978-3-642-65619-4 , p. 59.