Conoid

straight circle conoid: guide curve (red) is a circle, the axis (blue) is perpendicular to the alignment plane (yellow)

straight circular conoid (limited as in the first picture): outlines in 3-panel projection

A conoid (from the Greek κωνος cone and -ειδης similar) is a ruled surface in mathematics , whose family of generators (straight lines) the two additional conditions

(1) All generatrices of the surface are parallel to a plane, the straightening plane .
(2) All generatrices intersect a fixed straight line, the axis .

Fulfills.

The conoid is called straight if the axis is perpendicular to the alignment plane .

Because of (1) every conoid is a Catalan surface and can be represented by a parametric representation

${\ displaystyle \ mathbf {x} (u, v) = \ mathbf {c} (u) + v \ mathbf {r} (u) \,}$

to be discribed. Every surface curve with a fixed parameter is a generator, describes the guide curve and the vectors are all parallel to the straightening plane. The planarity of the vectors can be passed through with sufficient differentiability ${\ displaystyle \ mathbf {x} (u_ {0}, v)}$ ${\ displaystyle u = u_ {0}}$ ${\ displaystyle \ mathbf {c} (u)}$ ${\ displaystyle \ mathbf {r} (u)}$ ${\ displaystyle \ mathbf {r} (u)}$

{\ displaystyle \ det (\ mathbf {r}, \ mathbf {\ dot {r}}, \ mathbf {\ ddot {r}}) = 0}

express.

If the trajectory is a circle, it means Konoid Kreiskonoid .

Comment:

A conoid is unlimited (like a straight line). A graphic representation can therefore only ever show a finite part of the area.
The term conoid was coined by Archimedes in his treatise on conoids and spheroids .

Examples

Straight circular conoid

The parametric representation

{\ displaystyle \ mathbf {x} (u, v) = (\ cos u, \ sin u, 0) + v (0, - \ sin u, z_ {0}) \, \ 0 \ leq u <2 \ pi, v \ in \ mathbb {R}}

describes a straight Kreiskonoid with the unit circle in the xy plane as a guide curve and a plane parallel to the yz-plane directional plane . The axis is the straight line

{\ displaystyle (x, 0, z_ {0}) \ x \ in \ mathbb {R} \.}

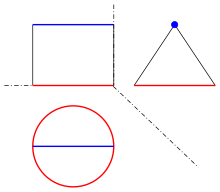
Special features : 1) Every horizontal section is an ellipse, 2) The outlines of the partial area shown in the picture with regard to the main directions are a rectangle, a circle and a triangle (see 2nd picture), 3) is an implicit representation, that is , the straight circular conoid is a surface of the 4th degree. 4) The Kepler barrel typically delivers in a straight Kreiskonoid with the base circle radius and height of the exact volume: . ${\ displaystyle (1-x ^ {2}) (z-z_ {0}) ^ {2} -y ^ {2} z_ {0} ^ {2} = 0}$ ${\ displaystyle r}$ ${\ displaystyle h}$ ${\ displaystyle V = {\ tfrac {\ pi} {2}} r ^ {2} h}$

The implicit representation is fulfilled by the whole straight line . There are no tangent planes at the points of this straight line . Such points are called singular . ${\ displaystyle (x, 0, z_ {0})}$

Hyperbolic paraboloid

hyperbolic paraboloid as conoid
red: guide curve, blue: axis, directional plane is parallel to the yz plane

The parametric representation

{\ displaystyle \ mathbf {x} (u, v) = (u, -1, -u) + v (0,1, u)}

{\ displaystyle = (u, v-1, u (v-1)), \ u, v \ in \ mathbb {R} \,}

describes the hyperbolic paraboloid with the equation It is a surface of the 2nd degree ( quadric ).

{\ displaystyle z = xy \.}

The leading curve of this conoid is the straight line (red in the picture), the straightening plane is parallel to the yz plane. If you choose the x-axis as the axis, the conoid is straight . Since in this example the further straight line runs through every point of the surface in addition to the generating line , one of these further straight lines can also be selected as the axis. However, only the first-mentioned axis is perpendicular to the plane of alignment. In this case the x-axis could be selected as both the guide curve and the axis. ${\ displaystyle (0, -1.0) + u (1.0, -1)}$ ${\ displaystyle \ mathbf {x} (u_ {0}, v_ {0})}$ ${\ displaystyle \ mathbf {x} (u_ {0}, v)}$ ${\ displaystyle \ mathbf {x} (u, v_ {0})}$

The hyperbolic paraboloid has no singular points.

Plücker conoid

Plücker conoid
red: guide curve, blue: axis,
the straightening plane is parallel to the xy plane

The parametric representation

{\ displaystyle \ mathbf {x} (u, v) = \ left (0,0, c \ sin u \ cos u) + v (\ cos u, \ sin u, 0 \ right)}

{\ displaystyle = \ left (v \ cos u, v \ sin u, c \ sin u \ cos u \ right) \, 0 \ leq u <\ pi \, \ v \ in \ mathbb {R} \, c > 0 \,}

represents a Plücker conoid with the equation

{\ displaystyle (x ^ {2} + y ^ {2}) z = c \; xy}

represent.

The guide curve is a path traversed twice on the z-axis, the axis of the conoid is the z-axis and the alignment plane is parallel to the xy-plane. Since the axis is perpendicular to the straightening plane, the conoid is straight .

The implicit representation is fulfilled by the entire z-axis. The points on the z-axis are singular (there are no tangent planes).

Whitney Umbrella

The parametric representation

{\ displaystyle \ mathbf {x} (u, v) = \ left (0,0, u ^ {2} \ right) + v \ left (u, 1,0 \ right)}

{\ displaystyle = \ left (uv, v, u ^ {2} \ right) \, u, v \ in \ mathbb {R} \,}

represents a Whitney Umbrella with the equation . The surface is a conoid with twice traversed the positive z-axis as a guide curve , the z-axis as the axis and a plane parallel to the xy plane directional plane . Since the axis is perpendicular to the straightening plane, this conoid is also straight . ${\ displaystyle x ^ {2} = y ^ {2} z}$

The implicit representation is also fulfilled by the negative z-axis, the handle of the umbrella. The points on the z-axis are singular (there are no tangent planes).

Parabolic conoid

parabolic conoid: guide curve is a parabola

The parametric representation

{\ displaystyle \ mathbf {x} (u, v) = \ left (1, u, -u ^ {2} \ right) + v \ left (-1.0, u ^ {2} \ right)}

{\ displaystyle = \ left (1-v, u, - (1-v) u ^ {2} \ right) \, u, v \ in \ mathbb {R} \,}

provides a parabolic conoid with the equation . The conoid having a parabola as a guide curve , the y-axis as the axis and parallel to the xz plane directional plane . Since the axis is perpendicular to the straightening plane, the conoid is straight . It is used in architecture as a roof surface (see Applications). ${\ displaystyle z = -xy ^ {2}}$

The parabolic conoid has no singular points.

Helical surface

The helical surface is also a straight conoid. It has no singularities.

Applications

Conoid in architecture

Conoids in architecture

In math

There are numerous simple examples of surfaces with singularities among the conoids .

In architecture

Like other ruled surfaces, conoids are used in architecture because they can be easily modeled from segments (beams, bars). Just Conoids can be very easily made: one threaded rods so on an axis that they can only rotate about this axis. Then you deflect the bars with the help of any guide curve and thus create a straight conoid. (See Parabolic Conoid.)

Web links

literature

Small Encyclopedia Mathematics , Harri Deutsch-Verlag, 1977, p. 219.