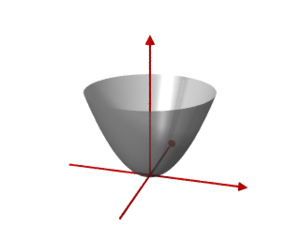
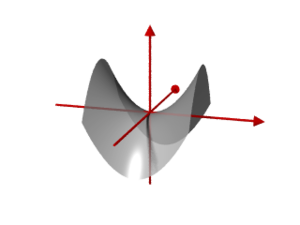
Paraboloid
A paraboloid is a surface of the second order (quadric) and is in the simplest cases either by an equation
- elliptical paraboloid , or
- hyperbolic paraboloid ,
described.
One encounters elliptical paraboloids as surfaces of satellite dishes .
Hyperbolic paraboloids are saddle surfaces . They contain straight lines and are therefore used by architects as easily modelable roof shapes ( hyperbolic parabolic shells ).
The equations show that both surfaces contain many parabolas , which contributed to the naming:
can be imagined as having arisen by rotating the parabola in the xz-plane with the equation around the z-axis. is not a surface of revolution. But with two exceptions, every section with a plane through the z-axis is also a parabola. For example, the intersection with the plane (yz plane) is the parabola .
Both surfaces (elliptical or hyperbolic) can be understood as sliding surfaces and can be generated by moving a parabola along a second parabola.
However, there are also significant differences:
- has circles as height sections ( ) . (In the general case there are ellipses (see below), which is reflected in the name affix),
- has hyperbolas or straight lines (for ) as height cuts , which justifies the addition hyperbolic .
One should not confuse a hyperbolic paraboloid with a hyperboloid .
Properties of P 1
Tangential planes at P 1
The tangent plane in a surface point on the graph of a differentiable function has the equation
- .
For the equation of the tangential plane at the point results
- .
Plane sections from P 1
The elliptical paraboloid is a surface of revolution and is created by rotating the parabola around the axis. A flat section of is:
- a parabola if the plane is perpendicular (parallel to the -axis).
- an ellipse or a point or empty if the plane is not perpendicular . A horizontal plane cuts in a circle .
- a point if the plane is a tangent plane .
Affine images of P 1
Any elliptical paraboloid is an affine image of . The simplest affine mappings are scaling of the coordinate axes. You provide the paraboloids with the equations
- .
still has the property that it is intersected by a perpendicular plane in a parabola. However, a horizontal plane cuts in an ellipse here, if the following applies. That any elliptical paraboloid always contains circles is shown in the circular section plane.
is
- symmetrical to the or coordinate planes.
- symmetrical to the -axis, d. H. leaves invariant.
- rotationally symmetric, if is.
Comment:
- A paraboloid of revolution (i.e. ) is of great technical importance as a parabolic mirror because all parabolas with the axis of rotation as an axis have the same focal point.
- If a glass filled with water is allowed to rotate around its axis of symmetry at a constant speed, the water rotates with the glass after a while. Its surface then forms a paraboloid of revolution.
- An elliptical paraboloid is often called a paraboloid for short .
- An elliptical paraboloid is projectively equivalent to the unit sphere (see projective quadric ).
Properties of P 2
Tangential planes at P 2
For is the equation of the tangential plane (see above) in the point
- .
Plane sections from P 2
is (in contrast to ) not a surface of revolution. But like are in almost all vertical plane sections parables:
The intersection of a plane with is
- a parabola if the plane is perpendicular (parallel to the -axis) and has an equation .
- a straight line if the plane is perpendicular and has an equation .
- an intersecting pair of lines if the plane is a tangential plane (see picture).
- a hyperbola , if the plane is not perpendicular and not a tangent plane (see picture).
Other properties
- The section parabolas with planes parallel to the or plane are all congruent to the norm parabola .
- is a sliding surface . is created by moving the parabola with its vertex along the parabola .
- A non-perpendicular plane that contains a straight line always contains a second straight line and is a tangential plane.
- Since the surface contains straight lines, it is a ruled surface .
- is a conoid .
- A hyperbolic paraboloid contains straight lines (like cylinders and cones), but cannot be developed (like cylinders and cones), since the Gaussian curvature is not present at every point . The Gaussian curvature is everywhere . (With a sphere the Gaussian curvature is everywhere .) Thus a hyperbolic paraboloid is a saddle surface .
- By rotating the coordinate system around the -axis by 45 degrees, the equation changes into the simpler equation .
Affine images of P 2
Any hyperbolic paraboloid is an affine image of . The simplest affine mappings are scaling of the coordinate axes. They provide the hyperbolic paraboloids with the equations
- .
is
- symmetrical to the or coordinate planes.
- symmetrical to the -axis, d. H. leaves invariant.
Comment:
- Hyperbolic paraboloids are used by architects for the construction of roofs (see picture) because they can easily be modeled with straight lines (bars).
- A hyperbolic paraboloid is projectively equivalent to a single-shell hyperboloid .
Hyperbolic paraboloid as an interpolation surface of 4 points
A hyperbolic paraboloid can also be understood as a bilinear interpolation surface of four points that are not in one plane :
- .
The network of parameter lines consists of straight lines.
For the image shown in the example . The hyperbolic paraboloid thus described has the equation .
Interface between families of elliptical and hyperbolic paraboloids
Leaves in the equations
- (Family of elliptical paraboloids)
and
- (Family of hyperbolic paraboloids)
the parameter run against , one obtains the equation of the common interface
- .
This is the equation of a cylinder with a parabola as a cross section (parabolic cylinder) , s. Image.

See also
- Hyperbolic paraboloid shell
- Paraboloid of revolution
- Ellipsoid
- Hyperboloid
- Rotational hyperboloid
- cone
- Conoid
- cylinder
literature
- ^ G. Farin: Curves and Surfaces for Computer Aided Geometric Design , Academic Press, 1990, ISBN 0-12-249051-7 , p. 250