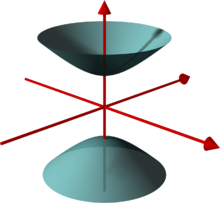
Hyperboloid
In the simplest case, a hyperboloid is a surface that is created by rotating a hyperbola around one of its axes.
- During rotation of a hyperbola around its side axis creates a hyperboloid. It consists of a contiguous piece of land.
- When a hyperbola rotates around its main axis, a double-shell hyperboloid is created. It consists of two separate patches.
Both surfaces can be described by a quadratic equation (analogous to the equations of ellipse and hyperbola). They are therefore special cases of quadrics ( sphere , cone , paraboloid , ...) and are typically intersected by planes in conic sections .
An essential difference between a single- or double-shell hyperboloid is:
- The single-shell hyperboloid contains straight lines, the double-shell hyperboloid does not.
This property makes the single-shell hyperboloid interesting for architects and civil engineers, as single-shell hyperboloids can easily be modeled from straight lines: e.g. B. Cooling towers (see pictures at the end of the article). Single-shell hyperboloids are also used in mechanical engineering for hyperboloid gears, single-shell hyperboloids also play a role in synthetic geometry: A Minkowski plane is the geometry of the flat sections of a single-shell hyperboloid. While the single-shell hyperboloid is intersected by tangential planes in two intersecting straight lines (see below), a double-shell hyperboloid with tangential planes only has one point in common and is therefore geometrically more related to a sphere.
Single-shell hyperboloid
Single-shell unit hyperboloid H1
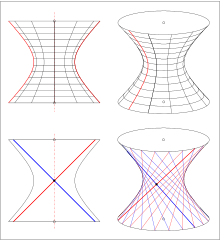
If the hyperbola is rotated in the xz-plane around its minor axis (ie z-axis) (see picture), the single-shell unit hyperboloid is obtained with the equation
- .
(When rotating, is replaced by .) Obviously, every vertical section with a plane is a circle with a radius . The intersection of the plane provides the two lines of intersection . By rotating this straight line, parametric representations of all straight lines on the hyperboloid are obtained:
The single-shell hyperboloid can also be created by rotating the straight line or ( skewed to the axis of rotation) (see picture). This statement is in the literature as set of Wren called.
Tangent planes of H1
The equation of the tangent plane of an implicitly given area at a point is .
For H1 it results
Flat sections from H1
- Planes with a slope less than 1 (1 is the slope of the straight line on the hyperboloid) intersect in an ellipse,
- Planes with an inclination equal to 1 intersect through the zero point in a parallel pair of lines,
- Planes with an inclination equal to 1 do not intersect through the origin in a parabola,
- Tangent planes intersect in an intersecting pair of lines,
- Planes with an inclination greater than 1, which are not tangent planes, intersect in a hyperbola.
A plane that contains a hyperboloid straight line is either a tangential plane and thus contains a second intersecting hyperboloid straight line or contains a hyperboloid straight line that is too parallel and is therefore a “tangential plane at a far point”.
Affine images of H1
Analogously to how any ellipse can be understood as an affine image of the unit circle, any single-shell hyperboloid is the affine image of the unit hyperboloid . The simplest affine images are obtained by scaling the coordinate axes:
Only in this case are the vertical sections still circles (otherwise ellipses). Such a hyperboloid is called a single-shell rotational hyperboloid . The fact that any single-shell hyperboloid always contains circles is shown in the circular section plane.
Since any single-shell hyperboloid (like the unit hyperboloid) contains straight lines, it is a ruled surface . Since every tangential plane (of a single-shell hyperboloid) intersects the surface in the vicinity of its point of contact, it has a negative Gaussian curvature and is therefore not developable, in contrast to the ruled surfaces cone or cylinder (Gaussian curvature 0). The following parametric representation of the hyperboloid is obtained from the usual parametric representation of a hyperbola with hyperbolic functions
Note: The single-shell hyperboloid and the hyperbolic paraboloid are projectively equivalent.
Double-shell hyperboloid
The two-shell unit hyperboloid H2
If the hyperbola of the xz-plane is rotated around its main axis (ie z-axis) (see picture), the two-shell unit hyperboloid is obtained with the equation or in the usual form
- .
The intersection of the plane with is a circle (if ) or a point (if ) or empty (if ). consists of two parts, corresponding to the two parts of the hyperbola.
Tangent planes of H2
The tangent plane of at a point has the equation (see above)
Plane sections of H2
- Planes with an inclination less than 1 (inclination of the asymptotes of the generating hyperbola) intersect either in an ellipse or in a point or not,
- Planes with an inclination equal to 1 and not intersecting through the origin
- Planes with an inclination equal to 1 and not intersecting the origin in a parabola,
- Planes with a slope greater than 1 intersect in a hyperbola.
Affine images of H2
An arbitrary two-shell hyperboloid is the affine image of Einheitshyperboloids . The simplest affine images are obtained by scaling the coordinate axes:
Only in this case are the non-trivial height sections still circles (otherwise ellipses). Such a hyperboloid is called a two-shell rotational hyperboloid. The fact that any two-shell hyperboloid always contains circles is shown in the circular section plane.
The following parameter representation results for a two-shell hyperboloid :
Note: The two-shell hyperboloid is projectively equivalent to the unit sphere.
Symmetry properties of the hyperboloids
Like ellipses and hyperbola, hyperboloids also have vertices and minor vertices and symmetries. The hyperboloids are obvious
- point-symmetrical to the origin of coordinates,
- symmetrical to the coordinate planes as well
- rotationally symmetrical to the z-axis and symmetrical to any plane through the z-axis, if is.
Double cone
The double cone can be as an interface between the crowds of single- and double-shelled hyperboloid or conceive. It arises from the rotation of the common asymptotes of the producer hyperbolas.
Common parameter representation
There are different possibilities. Parameterize hyperboloids. A simple way to parameterize the single-shell and double-shell hyperboloid and the cone is:
For there is a single-shell, for a two-shell hyperboloid and for a double cone.
See also
- Hyperbolic paraboloid shell
- Rotational hyperboloid
- Ellipsoid
- Paraboloid
- Paraboloid of revolution
- cylinder
- cone
- Confocal Quadrics
- NIGRES power line mast on the Oka
literature
- Albrecht Beutelspacher , Ute Rosenbaum: Projective geometry. From the basics to the applications (= Vieweg Studium: advanced course in mathematics ). 2nd, revised and expanded edition. Vieweg, Wiesbaden 2004, ISBN 3-528-17241-X ( online [accessed April 1, 2012]).
- Burkhard Polster: A geometrical picture book . 1st edition. Springer, New York / Berlin / Heidelberg 1998, ISBN 0-387-98437-2 .
- Hermann Schaal: Linear Algebra and Analytical Geometry . tape III . Vieweg, 1980, ISBN 3-528-13057-1 .
- Günter Scheja, Uwe Storch: Textbook of Algebra. Including linear algebra . 2., revised. and exp. Edition. Teubner, Stuttgart 1994, ISBN 3-519-12203-0 .
- Uwe Storch, Hartmut Wiebe: Textbook of Mathematics . 2., revised. and exp. Edition. BI-Wissenschafts-Verlag, 1999, ISBN 3-411-14101-8 .
Web links
- Eric W. Weisstein : Hyperboloid . In: MathWorld (English).
- Animated hyperboloid at EXOPAS. ( Memento of August 5, 2010 in the Internet Archive ).
Individual evidence
- ↑ W. Steinhilper (Ed.): Construction elements of mechanical engineering 2. Springer-Verlag, 2006, ISBN 3-540-29629-8 , p. 374.
- ↑ Model collection d. University of Göttingen: Hyperboloid gear
- ↑ K. Strubecker: Lectures of the Descriptive Geometry. Vandenhoeck & Ruprecht, Göttingen 1967, p. 218
- ↑ CDKG: Computer-aided Descriptive and Constructive Geometry. TU Darmstadt (PDF; 3.4 MB), p. 116.
- ↑ CDKG: Computer-aided Descriptive and Constructive Geometry. TU Darmstadt (PDF; 3.4 MB), p. 122.