Surface of revolution

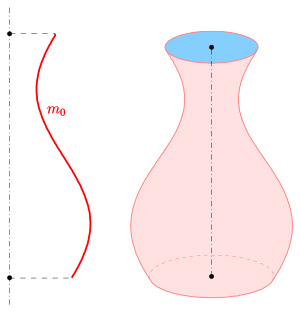
Rotation of a cos arc (see below)

Torus as a surface of revolution

A rotation surface or surface of revolution is in the geometry of a surface defined by rotation of a plane curve, of the main meridian , on a lying in the same plane line, the axis of rotation , is formed. A simple example is a straight circular cone. It is created by rotating a straight line around an axis of rotation that intersects it. Further simple examples are: straight circular cylinder (rotation of a straight line around an axis parallel to it), sphere (rotation of a circle around a diameter) and torus (rotation of a circle that does not intersect the axis). In comparison to other surfaces, surfaces of revolution have special properties:

• Rotational surfaces are rotationally symmetrical , ie the essential geometric information is already contained in the main meridian. They therefore have relatively simple analytical descriptions .
• A section with any plane that contains the axis of rotation is called a meridian and is always congruent to the main meridian.
• A cross section, i.e. H. a plane section with a plane perpendicular to the axis of rotation is always a circle and is called a circle of latitude .
• The meridians and parallels are the lines of curvature of the surface of revolution . (They intersect perpendicularly and give the directions of maximum and minimum normal curvatures at each point (see torus).)

Further examples: ellipsoid of revolution , paraboloid of revolution , hyperboloid of revolution .

Comment:

1. A surface of revolution can also be generated by rotating another suitable curve that is not in the same plane as the axis of rotation. A simple example is the hyperboloid of rotation. It can be generated by rotating a straight line lying on it (skewed to the axis of rotation). The generating straight line is not a meridian.
2. The outline of a surface of revolution is generally not a meridian or another plane section, see outline construction .

Analytical descriptions

Rotation of a point

The analytical description of a surface of revolution depends directly on the analytical description of the rotated plane curve, the main meridian. In the following it is always assumed that the z-axis is the axis of rotation .

If you let the point of the xz-plane rotate around the z-axis, you get the circle with radius . ${\displaystyle (r_{0},0,z_{0}),\ r_{0}\geq 0}$ ${\displaystyle (r_{0}\cos \varphi ,r_{0}\sin \varphi ,z_{0}),\ 0\leq \varphi <2\pi \ ,}$ ${\displaystyle r_{0}}$

Meridian in parametric form

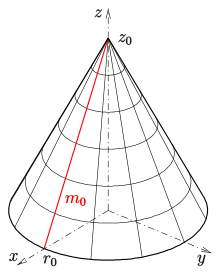
Cone as a surface of revolution

Ellipsoid as a surface of revolution

In this case it is assumed that

• the main meridian is the curve with . ${\displaystyle m_{0}}$ ${\displaystyle (r(t),0,z(t)),\ t_{1}\leq t\leq t_{2}}$ ${\displaystyle r(t)\geq 0}$

The parametric shape of the associated surface of revolution is then

• ${\displaystyle (r(t)\cos \varphi ,r(t)\sin \varphi ,z(t)),\ \ t_{1}\leq t\leq t_{2},0\leq \varphi <2\pi \ .}$

For geometrical considerations it is usually important to have a surface normal available. Under corresponding differentiability conditions, this results for a normal in a surface point ${\displaystyle (r\cos \varphi ,r\sin \varphi ,z)\ :}$

• ${\displaystyle {\vec {n}}=({\dot {z}}\cos \varphi ,{\dot {z}}\sin \varphi ,-{\dot {r}})\ .}$

For the surface area (without possible bottom and top circles!)

${\displaystyle A=2\pi \int _{t_{1}}^{t_{2}}r\ {\sqrt {{\dot {r}}^{2}+{\dot {z}}^{2}}}\,dt,}$.

Examples:

1) (distance) gives the cone ${\displaystyle m_{0}:(r_{0}t,0,z_{0}(1-t)),\ 0\leq t\leq 1}$

${\displaystyle (r_{0}t\cos \varphi ,r_{0}t\sin \varphi ,z_{0}(1-t),\ \ 0\leq t\leq 1,0\leq \varphi <2\pi \ ,}$

with base circle radius and height . ${\displaystyle r_{0}}$ ${\displaystyle z_{0}}$

2) (circle) gives the torus (see picture) ${\displaystyle m_{0}:(R+a\cos t,0,a\sin t),\ 0\leq t\leq 2\pi ,\ R>a}$

${\displaystyle ((R+a\cos t)\cos \varphi ,(R+a\cos t)\sin \varphi ,a\sin t),\ 0\leq t\leq 1,0\leq \varphi <2\pi \ .}$

3) (semi-ellipse) results in the ellipsoid of revolution ${\displaystyle m_{0}:(a\cos t,0,b\sin t),\ 0\leq t\leq \pi ,\ }$

${\displaystyle (a\cos t\cos \varphi ,a\cos t\sin \varphi ,b\sin t)\ 0\leq t\leq \pi ,\ 0\leq \varphi <2\pi \ .}$

4) (cosine curve) results ${\displaystyle m_{0}:(a\cos 2\pi {\tfrac {t-b}{l}}+c,0,t),\ 0\leq t\leq h,\ }$

${\displaystyle \left((a\cos 2\pi {\tfrac {t-b}{l}}+c)\cos \varphi ,(a\cos 2\pi {\tfrac {t-b}{l}}+c)\sin \varphi ,t\right)\ 0\leq t\leq h,\ 0\leq \varphi <2\pi \ .}$

For the first picture (vase) the following parameters were used:

${\displaystyle a=10,b=20,l=100,c=20,h=90}$

Meridian in implicit form

Surface of revolution, meridian = Cassini curve

In this case it is assumed that

• the main meridian is the curve implicitly given in the rz plane by the equation with . ${\displaystyle m_{0}}$ ${\displaystyle f(r,z)=0}$ ${\displaystyle r\geq 0}$

The implicit representation of the associated surface of revolution results from the replacement ${\displaystyle r={\sqrt {x^{2}+y^{2}}}\ :}$

• ${\displaystyle f({\sqrt {x^{2}+y^{2}}},z)=0\ .}$

A surface normal in a surface point is: ${\displaystyle (x,y,z)=(r\cos \varphi ,r\sin \varphi ,z)}$

• ${\displaystyle {\vec {n}}=(f_{r}\cos \varphi ,f_{r}\sin \varphi ,f_{z})\ .}$

Examples:

1) (distance) gives the cone with the equation ${\displaystyle m_{0}:z_{0}r+r_{0}z-r_{0}z_{0}=0,\ r_{0},z_{0}>0,\ 0\leq r\leq r_{0}\ ,}$

${\displaystyle z_{0}^{2}(x^{2}+y^{2})=r_{0}^{2}(z_{0}-z)^{2}\ ,}$the base circle radius and the height . ${\displaystyle r_{0}}$ ${\displaystyle z_{0}}$

2) (circle) gives the torus with the equation ${\displaystyle m_{0}:(r-R)^{2}+z^{2}-a^{2}=0,R>a>0\ ,}$

${\displaystyle (x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0\ .}$

3) ( Cassini curve ) gives the area with the equation ${\displaystyle m_{0}:(r^{2}+z^{2})^{2}-2c^{2}(r^{2}-z^{2})-(a^{4}-c^{4})=0,a>0,c>0\ ,}$

${\displaystyle (x^{2}+y^{2}+z^{2})^{2}-2c^{2}(x^{2}+y^{2}-z^{2})-(a^{4}-c^{4})=0}$

( Lemniscate ) was chosen for the picture . ${\displaystyle a=c=1}$

Guldinian rules

The first Guldin's rule , named after the Swiss mathematician Paul Guldin , enormously shortens the calculations of surfaces of rotation if the centers of gravity of the lines or areas of the rotating objects can be easily identified using the symmetries of the respective task.

Designations:

${\displaystyle A}$ = Area

${\displaystyle L}$ = Length of the generating line (profile line)

${\displaystyle R}$ = Radius of the center of gravity circle

${\displaystyle r}$ = Radius of the rotating circle (torus examples)

The area of a surface of revolution, whose axis of rotation does not intersect the generating line, is equal to the product of the length of the generating line (profile line) and the circumference of the circle (center of gravity circle), which is generated by the rotation of the center of gravity of the profile line: ${\displaystyle M}$

${\displaystyle A=L\cdot 2\pi R}$

Expressed as a function of the function of the generating line, the area results as: ${\displaystyle f}$

When rotating around the x axis

${\displaystyle A=2\pi \int _{a}^{b}f(x){\sqrt {1+\left[f'(x)\right]^{2}}}\mathrm {d} x}$

With as coordinate of the line center of gravity of the line and its line element one finds ${\displaystyle \textstyle R=y_{s}={\frac {1}{L}}\int _{L}y\mathrm {d} L}$ ${\displaystyle y}$ ${\displaystyle L}$ ${\displaystyle \mathrm {d} L}$

${\displaystyle A=L\cdot 2\pi R=L\cdot 2\pi \cdot {\frac {1}{L}}\int _{L}f(x)\mathrm {d} L=2\pi \int _{L}f(x)\mathrm {d} L}$,

what the above result represents if the interval limits are still used. ${\displaystyle \textstyle \mathrm {d} L={\sqrt {(\mathrm {d} x)^{2}+(\mathrm {d} y)^{2}}}={\sqrt {1+\left({\frac {\mathrm {d} y}{\mathrm {d} x}}\right)^{2}}}\mathrm {d} x}$ ${\displaystyle x}$ ${\displaystyle [a,b]}$

When rotating around the y- axis

${\displaystyle A=2\pi \int _{\min(f(a),f(b))}^{\max(f(a),f(b))}f^{-1}(y){\sqrt {1+\left[\left(f^{-1}(y)\right)'\right]^{2}}}\mathrm {d} y}$

As with the volume calculation above, the calculation for the continuous and strictly monotonous sections of in which the inverse function exists must also be carried out separately. ${\displaystyle f(x)}$

Example: Surface of a rotational torus :

${\displaystyle A=2\pi r\cdot 2\pi R=4\pi ^{2}rR}$

Parametric shape

If a curve is defined by its parametric shape in an interval , the areas of the surfaces of revolution that are generated by rotating the curve around the x-axis or the y-axis are given by ${\displaystyle (x(t),y(t))}$ ${\displaystyle [a,b]}$

${\displaystyle A_{x}=\int _{a}^{b}2\pi y\,{\sqrt {\left({\frac {\mathrm {d} x}{\mathrm {d} t}}\right)^{2}+\left({\frac {\mathrm {d} y}{\mathrm {d} t}}\right)^{2}}}\,\mathrm {d} t}$

${\displaystyle A_{y}=\int _{a}^{b}2\pi x\,{\sqrt {\left({\frac {\mathrm {d} x}{\mathrm {d} t}}\right)^{2}+\left({\frac {\mathrm {d} y}{\mathrm {d} t}}\right)^{2}}}\,\mathrm {d} t}$

Types

Rotational surfaces of constant Gaussian curvature were classified by Carl Friedrich Gauß and Ferdinand Minding . Surfaces of revolution with vanishing Gaussian curvature are the plane, the cylinder and the cone. The surfaces of revolution with positive Gaussian curvature are the spherical surface, the spindle-type surfaces, and the bead-type surfaces. Surfaces of revolution with negative Gaussian curvature are the pseudosphere , also known as Minding's surface, the cone-type surfaces, and the valley-type surfaces. The spherical surface and the pseudosphere have constant Gaussian curvature.

See also

• Body of revolution
• Outer surface

literature

• W. Kühnel: Differentialgeometrie , Vieweg-Verlag, Braunschweig / Wiesbaden, 2003, ISBN 3-528-17289-4 , p. 52
• Manfredo Perdigão do Carmo: Differential Geometry of Curves and Surfaces. Prentice-Hall Inc., Upper Saddle River NJ 1976, ISBN 0-13-212589-7 .
• Small encyclopedia of mathematics , Harri Deutsch-Verlag, 1977, p. 621
• Michael Spivak : A Comprehensive Introduction to Differential Geometry (Volume 3) , Publish or Perish Press, Berkeley, 1999, ISBN 0-914098-72-1
• Karl Strubecker : Differential Geometry (Volume III) , Göschen Collection, Volume 1180, De Gruyter, Berlin, 1959
• Rotary surfaces and ruled surfaces (PDF file; 777 kB) with formulas for calculating curvature and examples of rotational surfaces

Individual evidence

1. ^ Ravish R. Singh, Mukul Bhatt: Engineering Mathematics . A tutorial approach. Tata MacGraw Hill, New Delhi 2010, ISBN 978-0-07-014615-0 , pp. 6.90 (English, limited preview in Google Book Search).