Two-panel projection

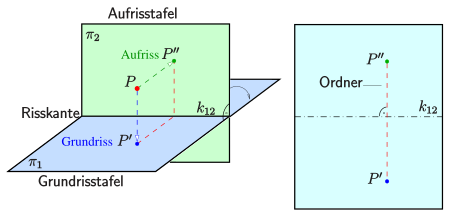
Floor plan and elevation in two-panel projection

The two-panel projection is a basic method of Descriptive Geometry . A point of the viewing area is projected onto two mutually perpendicular planes (image table) with the help of two perpendicular parallel projections. Usually the level is horizontal and is called the floor plan and vertical, the elevation board . The line of intersection is called the crack edge . The resulting pictures are floor plan or elevation of . ${\ displaystyle P}$ ${\ displaystyle \ pi _ {1}, \ pi _ {2}}$ ${\ displaystyle \ pi _ {1}}$ ${\ displaystyle \ pi _ {2}}$ ${\ displaystyle k_ {12} = \ pi _ {1} \ cap \ pi _ {2}}$ ${\ displaystyle P ', P' '}$ ${\ displaystyle P}$

If one imagines the xy-plane and the yz-plane, which intersect in the y-axis, one recognizes that in both projections (cracks) all spatial information (coordinates) of the point are contained. ${\ displaystyle \ pi _ {1}}$ ${\ displaystyle \ pi _ {2}}$ ${\ displaystyle P ', P' '}$ ${\ displaystyle P}$

Such cracks were already known to the Greeks and Romans. However, it was only an idea from Gaspard Monge that made it possible to graphically solve the essential spatial geometric problems of representational geometry relatively easily. Monge folded the elevation board around the crack edge into the floor plan and used the floor plan as a drawing plane. The initially spatial assignment of and is transferred to the assignment in the drawing plane by a folder (perpendicular to the crack edge). It is said that the floor plan and elevation are assigned to one another in the drawing level via the associated folder . ${\ displaystyle P '}$ ${\ displaystyle P ''}$ ${\ displaystyle P ', P' '}$

Ground plans and elevations of various points

Two-panel projection: different positions of points

Because the clarity of the position of points in the two-panel projection is significantly lower than in a spatially-acting image (axonometric), it takes some practice to the spatial position of a specific point by its base and elevation imagine. Normally one expects that in a two-panel projection the plan of a point is below and the plan of a point is above the crack edge. As examples in the picture show, this does not have to be the case. However, one always tries to optically separate the floor plan and elevation of an object in the two-panel projection (floor plan "below", elevation "above").

Straight lines

Two-panel projection of a straight line

Two-panel projection: different positions of straight lines

Two-panel projection of a straight line: track points

{\ displaystyle S_ {1}, S_ {2}}

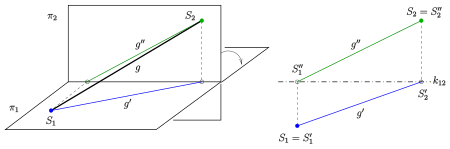
A straight line is uniquely determined by two points. So their ground plan and elevation are determined by the ground plan and elevation of two points.

Contour lines, front lines

There are several special positions of straight lines that are given special names (see picture):

A contour line is a straight line parallel to the base crack tabular runs. ${\ displaystyle \ pi _ {1}}$
A front line is a straight line which is parallel to to crack tabular runs. ${\ displaystyle \ pi _ {2}}$
A main straight line is a height or front line.
A Erstprojizierend e is a Perpendicular to the ground tore blackboard and a projection beam to the floor plan.
A Zweitprojizierende is a Perpendicular to On tore blackboard and a projection beam for the elevation.
A leaning straight line is contained in a plane perpendicular to the crack edge . Leaning straight lines are very uncomfortable in constructions, since both the floor plan and the elevation fall on the single folder (see picture). ${\ displaystyle k_ {12}}$ ${\ displaystyle \ pi _ {3}}$

Both height and front lines play a special role in determining true lengths , because

a segment on a treble line appears in the basic crack in true length.
a segment on a front line appears in the on crack in true length.

Main lines also play an important role in right angles because

A right angle appears again in the floor plan (elevation) as a right angle if a leg lies on a contour line (frontline).

Any angles appear in the floor plan (elevation) in true size if both legs are parallel to the floor plan (elevation table). Table parallelism can be achieved either by rotating the plane in which the angle lies around a contour line (front line) or by two rear projections (see true shape ).

Track points

The track points of a straight line are often used in constructions. They are the intersection points of the straight line with the crack panels. It always applies ${\ displaystyle S_ {1}, S_ {2}}$

${\ displaystyle S_ {1} = S_ {1} '\;, \ quad S_ {2} = S_ {2}' '\ quad}$ and

{\ displaystyle S_ {1} '' \;, \ quad S_ {2} '\ quad}

lie on the edge of the crack (see picture).

Levels

Description of a plane, track lines

Two-panel projection of a plane: tracks, main straight lines

a) normal in point b) perpendicular from point to plane ( given by)

{\ displaystyle n}

{\ displaystyle P}

{\ displaystyle l}

{\ displaystyle Q}

{\ displaystyle s_ {1}, s_ {2}}

Two-panel projection: special positions of planes

A plane is usually described in the representational geometry by a triangle or two intersecting straight lines in plan and elevation. In the second case, you choose main straight lines (contour lines, front lines) or track straight lines (intersection of the plane with the crack plates, see picture). Here, too, it takes some practice to be able to imagine the position of the plane in space from the given floor plans and elevations (see picture).

The following applies to straight lines on a plane: ${\ displaystyle s_ {1}, s_ {2}}$

${\ displaystyle s_ {1} = s_ {1} ', s_ {2} = s_ {2}' '}$ and

{\ displaystyle s_ {1} '', s_ {2} '}

coincide with the crack edge and are mostly left out (see picture).

The following properties are often useful for constructions with planes:

The front lines of a level are all parallel to each other, especially to the tear-open track (see picture). ${\ displaystyle s_ {2}}$
The contour lines of a level are all parallel to one another, especially to the ground plan track . ${\ displaystyle s_ {1}}$

Plumb line on a plane, distance point to plane

Since the crack (vertical parallel projection) of a right angle is only a right angle again if one leg is parallel to the image table (see section on straight lines), the following applies (see picture)

The plan of a perpendicular on a plane is perpendicular to any height line of the plane.
The elevation of a perpendicular to a plane is perpendicular to any front line of the plane.

If you want to determine the distance of a point from a plane, you have to cut the perpendicular to the plane with the plane (see: intersection point construction ). The point of intersection is the plumb line . The true length of the line (perpendicular) is the sought-after distance of the point from the plane. ${\ displaystyle Q}$ ${\ displaystyle Q}$ ${\ displaystyle F}$ ${\ displaystyle {\ overline {QF}}}$

Plumb line, plumb line on a straight line, distance point-straight line

Will you, the solder from a point of a straight cases (in the room), one can use the level by which to perpendicular is as auxiliary plane. is a perpendicular plane of . It applies ${\ displaystyle Q}$ ${\ displaystyle g}$ ${\ displaystyle \ varepsilon}$ ${\ displaystyle Q}$ ${\ displaystyle g}$ ${\ displaystyle \ varepsilon}$ ${\ displaystyle g}$

The outline of the contour line from through is perpendicular to . ${\ displaystyle h_ {1} '}$ ${\ displaystyle h_ {1}}$ ${\ displaystyle \ varepsilon}$ ${\ displaystyle Q}$ ${\ displaystyle g '}$

( is parallel to the crack edge!)

{\ displaystyle h_ {1} ''}

The front line elevation from through is perpendicular to . ${\ displaystyle h_ {2} ''}$ ${\ displaystyle h_ {2}}$ ${\ displaystyle \ varepsilon}$ ${\ displaystyle Q}$ ${\ displaystyle g ''}$

( is parallel to the crack edge!)

{\ displaystyle h_ {2} '}

This means that the plane through the height and front line is fixed in the point . With the help of the piercing point construction , the plumb point can then be determined. The distance of the point Q from the straight line is the true length of the line . How to determine a true length can be found here . ${\ displaystyle \ varepsilon}$ ${\ displaystyle Q}$ ${\ displaystyle F = g \ cap \ varepsilon}$ ${\ displaystyle g}$ ${\ displaystyle {\ overline {QF}}}$

Re-projection, three-panel projection

Reprojection a point (elevation new: )

{\ displaystyle P '' '}

Projection of a rhomb dodecahedron and true shape of a rhombus

There are two basic tasks in descriptive geometry that can be solved by introducing a new crack. This is explained using the example of the rhombic dodecahedron (see below). The rhombic dodecahedron is given by assigned cracks (ground plan and elevation). We are looking for 1) a clear crack (orthogonal projection) and 2) the true shape of one of the 12 rhombuses.

First of all it is explained how to construct a new plan of a point given in plan and elevation.

Introduction of a new layout

Given: A point in the floor plan and elevation ( , crack edge ) and a new elevation board through the crack edge . ${\ displaystyle P}$ ${\ displaystyle P ', P' '}$ ${\ displaystyle k_ {12}}$ ${\ displaystyle \ pi _ {3}}$ ${\ displaystyle k_ {13}}$

Wanted: The new layout . ${\ displaystyle P '' '}$

${\ displaystyle P '}$ and are therefore assigned to one another via a folder (Lot to ). ( are not assigned to each other!) ${\ displaystyle P '' '}$ ${\ displaystyle k_ {13}}$ ${\ displaystyle P '', P '' '}$

From the picture you can see

${\ displaystyle P '' '}$ lies on the folder (perpendicular to through ) at the same distance as the old elevation from the old tear edge (see picture). ${\ displaystyle k_ {13}}$ ${\ displaystyle P '}$ ${\ displaystyle k_ {13}}$ ${\ displaystyle P ''}$ ${\ displaystyle k_ {12}}$

Example rhombic dodecahedron:
In the example shown here a rhombic dodecahedron is given in plan and elevation.

1) Illustrative outline

Both of the given cracks are easy to draw, but they cannot be visualized because many pairs of points coincide in the elevation or floor plan. Another elevation is defined by inserting the new crack edge . (The new crack edge can be chosen almost arbitrarily. It should just not be parallel and not perpendicular to the ground plan of one of the polyhedron edges.) In the new crack there are no longer any points behind one another. This makes it easier to see the individual rhombuses and their position in space. (When creating the new elevation, use can be made of the fact that each of the 3 squares is at the same height and therefore has the same distance to the new edge of the tear.) ${\ displaystyle k_ {13}}$ ${\ displaystyle \ {B, C, D, E \}, \ {F, G, H, I \}, \ {J, K, L, M \}}$

2) true shape of a rhombus

Obviously the rhombus lies in a vertical plane. If a new elevation plane is introduced in such a way that it is parallel to the rhombus , the rhombus must appear in its true form in the new crack. So you choose a new crack edge parallel to and construct the new elevation of the four points . The rhombus has the true shape of the rhombs. ${\ displaystyle FKGC}$ ${\ displaystyle FKGC}$ ${\ displaystyle k_ {14}}$ ${\ displaystyle F'G '}$ ${\ displaystyle FKGC}$ ${\ displaystyle F '' '' K '' '' G '' '' C '' ''}$

Cross plan and three-panel projection

Cross plan, three-panel projection

Is the new crack panel perpendicular to the floor plan and the elevation panel, i.e. H. , is called the new elevation cross elevation (see picture) and assigns it directly to the existing elevation. An allocation of the new plan to the floor plan is obtained by concentric circular arcs as a folder (see picture). This means that information from any crack can now be transferred to the other two cracks via the corresponding folders. Such an arrangement is called a three-panel projection . ${\ displaystyle k_ {23} \ perp k_ {12}}$

literature

Rudolf Fucke, Konrad Kirch, Heinz Nickel: Descriptive Geometry. Fachbuch-Verlag, Leipzig 1998, ISBN 3-446-00778-4 , p. 10.
Cornelie Leopold: Geometric Basics of Architectural Representation. Verlag W. Kohlhammer, Stuttgart 2005, ISBN 3-17-018489-X , p. 40.
Ulrich Graf, Martin Barner: Descriptive Geometry. Quelle & Meyer, Heidelberg 1961, ISBN 3-494-00488-9 , p. 59.

Web links

Descriptive geometry for architects (PDF; 1.5 MB). Script (Uni Darmstadt), pp. 23–34.
Fundamentals and elements of traffic engineering ( Memento from August 10, 2013 in the Internet Archive ) (PDF; 493 kB) TU Dresden
Three-panel projection at the University of Duisburg-Essen

Individual evidence

↑ see Geometry descriptive . P. 10

[1] see Geometry descriptive . P. 10