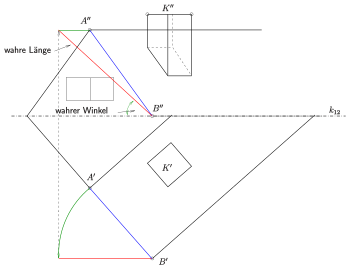
True length (descriptive geometry)
The true length is understood in the representational geometry to be the actual length of a route in space given in plan and elevation (see two-panel projection ). If the route is parallel to the elevation board or floor plan, it appears unabridged in the elevation or floor plan. For the general (deviating) case, there are two ways to graphically determine the true length of a line . Both are described here using the same example:
In the first drawing there are two points and are given in plan and elevation. The route is neither parallel to the elevation nor to the floor plan. The two other drawings show the two possible solutions.
1st possibility
The route is rotated around an axis perpendicular to the floor plan (or elevation table) until it is parallel to the elevation table (or floor plan). The rotated route then appears undistorted in the elevation, i.e. H. the length of the route is the true length.
Performing the rotation:
- Turn around until the track is parallel to the edge of the crack . Let the rotated point be (plan of , the rotated point ).
- lies on the folder through and on the parallels through to the edge of the tear (when turning, remains at the same height as !).
- is the true length of the route .
2nd possibility
You construct the point in plan and elevation that lies below the point at the height of . The right triangle is the supporting triangle of the stretch (one leg is vertical, the second is horizontal). If you turn the support triangle around the contour line into a horizontal position , the true length is. Execution:
- Draw the elevation of the point that is vertically below and is the same height as . It is .
- Turn the right-angled triangle around the cathetus so that it is parallel to the floor plan by plotting the line vertically. The length of the hypotenuse of the resulting (right-angled) triangle is the true length.
Comment:
- With both methods, the true angle of inclination of the route can also be seen.
- By reversing this method, true lengths can also be plotted .
- In terms of calculations , determining the length of a route is an easy task. This is because the coordinates of the points can be measured from the outline and elevation with respect to a given coordinate system and calculated using the Euclidean distance formula.
Note: True lengths can also be determined for central projections (see Reconstruction (Descriptive Geometry) ).
See also
literature
- Rudolf Fucke, Konrad Kirch, Heinz Nickel: Descriptive geometry for engineers . 17th edition. Carl Hanser, Munich 2007, ISBN 3-446-41143-7 , p. 39 f . ( online at google-books [accessed on May 31, 2013]).
- Cornelie Leopold: Geometric Basics of Architectural Representation . 4th edition. Vieweg + Teubner, Wiesbaden 2012, ISBN 978-3-8348-1838-6 , pp. 102 ( online at google-books [accessed on May 31, 2013]).
Web links
- Descriptive geometry for architects (PDF; 1.5 MB). Script (Uni Darmstadt)
- Descriptive geometry for civil engineers (PDF; 1.2 MB). Script (Uni Darmstadt)