spiral

The title of this article is ambiguous. Further meanings are listed under spiral (disambiguation) .

The calcareous shell of the ammonites is built up almost like a logarithmic spiral

A spiral or helix is a curve that runs around a point or an axis and, depending on the perspective of the observer, moves away from or approaches this center.

Spiral or screw

The spiral is sometimes confused with the screw . While the prototypical spiral is a structure in the plane, such as the groove of a record or the arms of a spiral galaxy , both the screw and the twist drill are three-dimensional structures along the courtyard of a cylinder. The demarcation to a vortex wheel is ultimately unclear.

Plane spirals

Descriptions

Archimedean spiral

Mathematically, spirals can best be described as coordinate equations in the plane polar coordinate system, where is represented as a function of ; generally runs to infinity instead of just 2π. Negative angles are also possible. ${\displaystyle r}$ ${\displaystyle r(\varphi )}$ ${\displaystyle \varphi }$ ${\displaystyle \varphi }$

Polar representation of a spiral:

• ${\displaystyle r=r(\varphi )}$

In - -coordinates thereby become points with the parametric representation ${\displaystyle x}$ ${\displaystyle y}$

• ${\displaystyle x=r(\varphi )\cos \varphi \ ,\qquad y=r(\varphi )\sin \varphi }$

described.

Replacing in the polar representation by , the spiral is the angle rotated. (The definition range may have to be adjusted.) ${\displaystyle \varphi }$ ${\displaystyle \varphi -\varphi _{0}}$ ${\displaystyle \varphi _{0}}$

Examples

• Archimedean spiral : ${\displaystyle \ r=a\varphi }$
• Hyperbolic spiral : ${\displaystyle \ r={\tfrac {a}{\varphi }}}$
• Fermatsche spiral : ${\displaystyle \ r=a{\sqrt {\varphi }}}$
• Lituus spiral : ${\displaystyle \ r={\tfrac {a}{\sqrt {\varphi }}}}$
• Logarithmic spiral : ${\displaystyle \ r=ae^{k\varphi }}$

Hyperbolic spiral as central projection of a helical line

The Archimedean spiral arises z. B. when winding up an evenly thick carpet. It is described in the - -plane by a straight line. ${\displaystyle r}$ ${\displaystyle \varphi }$

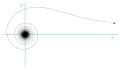
The hyperbolic spiral is described in the - plane by a hyperbola. It arises from the central projection of a helical line onto a plane perpendicular to the screw axis (see picture). You can see them e.g. B. when looking vertically through a spiral staircase (see helical line (descriptive geometry) ). It is also the image of an Archimedean spiral when mirrored in a circle (inversion). ${\displaystyle r}$ ${\displaystyle \varphi }$

The Fermat's spiral is also called a parabolic spiral, since its polar equation describes a parabola.

The lituus spiral is the image of a Fermat spiral in a mirrored circle.

The logarithmic spiral is created e.g. B. in the growth of snail shells. Your name is due to the dissolution of their polar equation to her: . ${\displaystyle \varphi }$ ${\displaystyle \varphi ={\tfrac {1}{k}}\cdot \ln {\tfrac {r}{a}}}$

• 

  Hyperbolic spiral:
  ${\displaystyle r={\frac {a}{\varphi }}}$

• 

  Fermatsche spiral:
  ${\displaystyle r=a{\sqrt {\varphi }}}$

• 

  Lituus spiral:
  ${\displaystyle r={\frac {a}{\sqrt {\varphi }}}}$

• 

  Logarithmic spiral:
  ${\displaystyle r=ae^{k\varphi }}$

In addition to these spirals, there are also some that do not fit into this concept:

• Spiral of Theodorus . It is not a smooth curve, but a polygon with side lengths 1.
• Clothoid (Cornu spiral). It has two asymptotic points.

• 

  Spiral of Theodorus

• 

  Cornu spiral

properties

Polar coordinates: definition of sector (light blue) and polar slope angle ( ) ${\displaystyle \alpha }$

Polar slope angle

The angle at which the spiral tangent intersects the associated polar circle is called the polar slope angle and the polar slope. The formula for the tangent vector results ${\displaystyle \alpha }$ ${\displaystyle \tan \alpha }$

${\displaystyle \tan \alpha ={\frac {r'}{r}}\ .}$

For a spiral with the equation is the polar slope ${\displaystyle \;r=a\varphi ^{n}\;}$

• ${\displaystyle \tan \alpha ={\frac {n}{\varphi }}\ .}$

For the Archimedean spiral is and thus ${\displaystyle n=1}$ ${\displaystyle \;\tan \alpha ={\tfrac {1}{\varphi }}\ .}$

For the logarithmic spiral is constant. ${\displaystyle \ \tan \alpha =k\ }$

curvature

The curvature of a curve in polar representation is ${\displaystyle \kappa }$

${\displaystyle \kappa ={\frac {r^{2}+2(r')^{2}-r\;r''}{(r^{2}+(r')^{2})^{3/2}}}\ .}$

For a spiral with the equation we get ${\displaystyle r=a\varphi ^{n}}$

• ${\displaystyle \kappa =\dotsb ={\frac {1}{a\varphi ^{n-1}}}{\frac {\varphi ^{2}+n^{2}+n}{(\varphi ^{2}+n^{2})^{3/2}}}\ .}$

Eg is for (Archimedean spiral) . So the spiral has no turning point. ${\displaystyle n=1}$ ${\displaystyle \kappa ={\tfrac {\varphi ^{2}+2}{a(\varphi ^{2}+1)^{3/2}}}}$

The curvature of a logarithmic spiral is ${\displaystyle \;r=ae^{k\varphi }\;}$ ${\displaystyle \;\kappa ={\tfrac {1}{r{\sqrt {1+k^{2}}}}}\;.}$

Sector area

The area of ​​a curve sector of a curve in polar representation is

${\displaystyle A={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}r(\varphi )^{2}\;d\varphi \ .}$

For a spiral with the equation we get ${\displaystyle r=a\varphi ^{n}\;}$

• ${\displaystyle A={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}a^{2}\varphi ^{2n}\;d\varphi ={\frac {a^{2}}{2(2n+1)}}{\big (}\varphi _{2}^{2n+1}-\varphi _{1}^{2n+1}{\big )}\ ,\quad {\text{falls}}\quad n\neq -{\frac {1}{2}},}$
• ${\displaystyle A={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}{\frac {a^{2}}{\varphi }}\;d\varphi ={\frac {a^{2}}{2}}(\ln \varphi _{2}-\ln \varphi _{1})\ ,\quad {\text{falls}}\quad n=-{\frac {1}{2}}\ .}$

The sector area of ​​a logarithmic spiral is ${\displaystyle \;r=ae^{k\varphi }\;}$ ${\displaystyle \ A={\tfrac {r(\varphi _{2})^{2}-r(\varphi _{1})^{2})}{4k}}\ .}$

Arc length

The length of an arc of a curve in polar representation is

${\displaystyle L=\int \limits _{\varphi _{1}}^{\varphi _{2}}{\sqrt {\left(r^{\prime }(\varphi )\right)^{2}+r^{2}(\varphi )}}\,\mathrm {d} \varphi \ .}$

For a spiral with the equation we get ${\displaystyle r=a\varphi ^{n}\;}$

• ${\displaystyle L=\int _{\varphi _{1}}^{\varphi _{2}}{\sqrt {{\frac {n^{2}r^{2}}{\varphi ^{2}}}+r^{2}}}\;d\varphi =a\int \limits _{\varphi _{1}}^{\varphi _{2}}\varphi ^{n-1}{\sqrt {n^{2}+\varphi ^{2}}}d\varphi \ .}$

These integrals are no longer solvable for everyone . In the case of Fermat's spiral, an elliptical integral results . ${\displaystyle n}$

The arc length of a logarithmic spiral is ${\displaystyle \;r=ae^{k\varphi }\;}$ ${\displaystyle \ L={\tfrac {\sqrt {k^{2}+1}}{k}}{\big (}r(\varphi _{2})-r(\varphi _{1}){\big )}\ .}$

Limited spirals

Constrained spirals: (left), (right)
${\displaystyle r=a\arctan(k\varphi )}$
${\displaystyle r=a(\arctan(k\varphi )+\pi /2)}$

The function of a spiral is usually a strictly monotonic , continuous function and unlimited . In the standard examples, there is a power function or an exponential function. However, one can also choose for a restricted, strictly monotonous function and thus obtain a restricted spiral. A suitable function for this is the arctangent : ${\displaystyle r(\varphi )}$ ${\displaystyle r(\varphi )}$ ${\displaystyle r(\varphi )}$

example 1

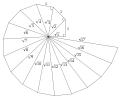
If you place and choose , you get a spiral that starts at the origin (like the Archimedean spiral) and approaches the circle with a radius (left in the picture). ${\displaystyle \;r=a\arctan(k\varphi )\;}$ ${\displaystyle \;k=1/10,\;a=4,\;\varphi \geq 0}$ ${\displaystyle \;r=2\pi \;}$

Example 2

If you place and choose , you get a spiral that approaches the origin (like the hyperbolic spiral) and approaches the circle with radius (in the picture on the right). ${\displaystyle \;r=a(\arctan(k\varphi )+\pi /2)\;}$ ${\displaystyle \;k=1/5,\;a=2,\;-\infty <\varphi <\infty }$ ${\displaystyle \;r=2\pi \;}$

Spatial spirals

Conical spiral with Archimedean spiral as a plan

Conical spirals

→ Main article : Conical spiral

Is in the - level through the parametric representation ${\displaystyle x}$ ${\displaystyle y}$

${\displaystyle x=r(\varphi )\cos \varphi \ ,\qquad y=r(\varphi )\sin \varphi }$

Given a plane spiral, a third coordinate can be added so that the resulting spatial curve lies on the vertical circular cone with the equation : ${\displaystyle z(\varphi )}$ ${\displaystyle \;m^{2}(x^{2}+y^{2})=(z-z_{0})^{2}\ ,\ c>0\;}$

• ${\displaystyle x=r(\varphi )\cos \varphi \ ,\qquad y=r(\varphi )\sin \varphi \ ,\qquad \color {red}{z=z_{0}+mr(\varphi )}\ .}$

Spirals of this type are called conical spirals. They were already known to Pappos .

example

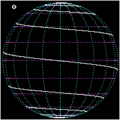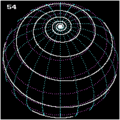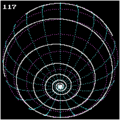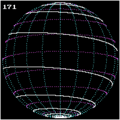
Assuming an Archimedean spiral , the conical spiral is obtained (see picture) ${\displaystyle \;r(\varphi )=a\varphi \;}$

${\displaystyle x=a\varphi \cos \varphi \ ,\qquad y=a\varphi \sin \varphi \ ,\qquad z=z_{0}+ma\varphi \ ,\quad \varphi \geq 0\ .}$

In this case, the conical spiral can also be understood as the intersection of a cone and a helical surface .

Spherical spiral with ${\displaystyle c=8}$

Spherical spirals

If you represent a sphere with a radius in spherical coordinates: ${\displaystyle r}$

${\displaystyle {\begin{aligned}x&=r\cdot \sin \theta \cdot \cos \varphi \\y&=r\cdot \sin \theta \cdot \sin \varphi \\z&=r\cdot \cos \theta \end{aligned}}}$

and if there is a linear dependency of the angle , a spherical spiral with the parametric representation is obtained ${\displaystyle \;\varphi =c\theta ,\;c>2\;}$

• ${\displaystyle {\begin{aligned}x&=r\cdot \sin \theta \cdot \cos {\color {red}c\theta }\\y&=r\cdot \sin \theta \cdot \sin {\color {red}c\theta }\\z&=r\cdot \cos \theta \qquad \qquad 0\leq \theta \leq \pi \ .\end{aligned}}}$

Spherical spirals have also been examined by Pappus. They are special Clelia curves .

Allowed so to, you get a vivianische curve . ${\displaystyle c=1}$ ${\displaystyle \;\varphi =\theta \;}$

Please note: A Loxodrome is not a spherical spiral in the sense explained here.

• 

  Spherical spiral

• 

  Loxodrome

In art

Unlike in nature and in most of the geometrical constructions, in art there are also inward and outward-turning double spirals.

Prehistory and Antiquity

Newgrange - stone at the entrance.
In the left half of the picture a triple spiral ( triskele ) is already indicated .

Vase decorated with spirals from the Egyptian Naqada II period

Spirals appeared as a common ornamental motif on stone and ceramics in prehistoric times . Examples can be found in the ribbon ceramics of the Neolithic, but also in the early advanced cultures of Egypt , Crete and China . In Europe, spiral motifs are widespread from the megalithic cultures through the Bronze Age to the Early Iron Age as well as among the Celts and Teutons and also appear on Iberian ceramics.

Spirals convey an idea of ​​infinity, but they can also be meant to protect against disasters ( apotropaic ) or even function as tribal symbols.

Triple and multiple spirals

Triple spiral as a prehistoric motif ( triskele ) or Celtic triskele

A Gotland picture stone was found in the church of Vallstena , the middle part of which is decorated with a four-fold spiral ornament. The symbol, which is much older as a triple spiral and occurs to some extent in the passage tomb of Newgrange in Ireland, can be found on Gotland as a 4, 6 and 7-fold combination. Stylized animal heads and more realistic images of people and animals are sometimes combined with this geometric motif. The spiral, like the vortex wheel , is probably a sun symbol or the representation of a multitude of gods. Color supported the flat but finely carved ornament and highlighted the image. The spiral motif occurs in various forms and compositions on the older stones, which were made between AD 400 and 600. However, spiral motifs appear both earlier and later in different contexts of finds. They are common in the British Isles around the birth of Christ, and in late Celtic art several centuries younger they can be studied in early Christian manuscripts. This art is closer in time to the picture stones; it has therefore been suggested that there is some connection.

Spiral motifs in the Middle Ages

In European art of the Middle Ages ( Romanesque and Gothic ) spiral motifs are rarely found, although - especially in Gothic tracery  - geometric games (ludi geometrici) were common and in the late Gothic period also led to centered and drawn three-pass shapes, which are reminiscent of older spiral motifs to wake up. On the other hand, labyrinths , braids , tendrils and other winding, but very often - unlike the spirals - overlapping decorative motifs are increasing in number. In the tympanum field of the church of Bembrive ( Pontevedra province , Spain) three spirals can be seen; the front of the inner arch of the portal of the Church of San Pedro de Gaíllos ( Segovia province , Spain) shows - in addition to rosettes and vertebrae - also small spirals. They are more common on medieval door and chest fittings - but there they develop from straight bands.

• 

  Capital in Zvartnots , Armenia (7th century)

• 

  Portal of the Church of San Pedro de Gaíllos , detail

• 

  The tympanum of the Bembrive church

• 

  Capital of the Church of Franchesse

• 

  Spiral fittings on the door of the Navata Church

• 

  Spiral fittings on the door of the church of Prats-de-Mollo-la-Preste

Renaissance, Baroque, Art Nouveau

In the Renaissance, the spiral found its way into the arabesque and grotesque , in architecture it can be found in the volute as well as in scrollwork and in mannerism in the characteristic figura serpentinata . Spirals in the volutes of the Baroque and Art Nouveau periods (e.g. in Gustav Klimt ) experience late highlights .

Friedensreich Hundertwasser used the spiral as a symbol of birth and death in his own art style and loved it because it counteracted the straight line.

Social sciences

In the polls the metaphor " spiral of silence " was used by Elisabeth Noelle-Neumann to explain and at the same time to combat a certain mutual build-up of social reactions: In public opinion certain minority standpoints are so emphatically represented that the majority hesitates to stand at all to say that the minority would become more and more dictatorial and the majority more and more mute, etc. This connection is very difficult to verify empirically.

In general, every mechanism that causes an escalation of the situation is referred to as a spiral, for example "spiral of violence". In systems science , harmonic oscillators that grow (escalate) exponentially show logarithmic spirals in their phase space diagrams (escalation spirals ). Therefore, this term is mathematically more correct than the synonymously used term “ vicious circle ”, which does not contain any escalation of the states.

In the nature

Shell of a snail

Sunflower with 34 and 55 Fibonacci 'spirals' (better: 'whirls')

Many plants and some animals have spiral structures in their blueprint, such as the snail shell . Fossil examples are the ammonites . The “arrangement” of these biologically generated spirals, which are mostly based on logarithmic spirals, is again in the vast majority of cases as a Fibonacci sequence .

Furthermore - often three-dimensionally connected with chirality :

• Cochlea (Latin cochlea) of the ear in the inner ear of mammals
• The horn of some kinds of sheep

In physics, an electrically charged particle that moves in a magnetic field follows a spiral path. The prerequisite is that the particle does not move parallel, anti-parallel or transverse to the north-south orientation of the magnetic field. The force that forces the particle on a spiral path is called the Lorentz force . Strictly speaking, this trajectory is a helix . When moving parallel or anti-parallel to the north-south orientation of the magnetic field, a straight trajectory is created, and when moving transversely to the north-south orientation of the magnetic field, a circular path is created. When an electrically charged particle emits energy through electromagnetic radiation on such a circular path, it moves on an increasingly narrow spiral path. The helical trajectory of the electrically charged particle is a superposition of a straight trajectory and a circular path. In the event of energy losses through electromagnetic radiation, and also in inhomogeneous magnetic fields, conical spirals arise from the superposition of screw and spiral.

See also

• whirl
• Ulam spiral
• Intrauterine device , also known colloquially as a “coil”, is a method of contraception

Web links

Commons : Spirals and Screws  - collection of images, videos and audio files

• Math tinkering: spirals. On: Mathematische-Basteleien.de.
• Examples of spirals in the plant kingdom. On: Maven.Smith.edu.
• Vi Hart: Doodling in Math: Spirals, Fibonacci, and Being a Plant. On: YouTube.com.
• Jamnitzer gallery: 3D spirals.

Individual evidence

1. ^ Siegmund Günther, Anton Edler von Braunmühl, Heinrich Wieleitner: History of Mathematics. GJ Göschen, 1921, p. 92.
2. ↑ Kuno Fladt: Analytical geometry of special surfaces and space curves. Springer-Verlag, 2013, ISBN 978-3-322-85365-3 , p. 132.
3. ↑ ^{a b} Wolf Stadler among others: Lexicon of Art 11th Sem - Tot. Karl Müller Verlag, Erlangen 1994, ISBN 3-86070-452-4 , p. 113.
4. ^ Henri Brunner: Right or left - in nature and elsewhere. Wiley-VCH, Weinheim 1999, ISBN 3-527-29974-2 , pp. 45-65.