Conical spiral

Conical spiral with Archimedean spiral as a plan

Ground plan: Fermatsche spiral

Ground plan: logarithmic spiral

Ground plan: hyperbolic spiral

A conical spiral is a curve on a perpendicular circular cone , the outline of which is a plane spiral . If the ground plan is a logarithmic spiral , it is called a concho spiral, derived from conch (water snail).

Like the logarithmic spiral itself, the concho spiral constructed with it also plays a role in biology in the modeling of snail shells , in insect flight and in technology in the construction of broadband antennas .

Parametric representation

Is in the - level through the parametric representation ${\displaystyle x}$ ${\displaystyle y}$

${\displaystyle x=r(\varphi )\cos \varphi \ ,\qquad y=r(\varphi )\sin \varphi }$

Given a plane spiral, a third coordinate can be added so that the resulting spatial curve lies on the vertical circular cone with the equation : ${\displaystyle z(\varphi )}$ ${\displaystyle \;m^{2}(x^{2}+y^{2})=(z-z_{0})^{2}\ ,\ m>0\;}$

• ${\displaystyle x=r(\varphi )\cos \varphi \ ,\qquad y=r(\varphi )\sin \varphi \ ,\qquad \color {red}{z=z_{0}+mr(\varphi )}\ .}$

Curves of this type are called conical spirals and the plane spiral used for construction is their plan. They were already known to Pappos .

The parameter is the slope of the taper line compared to the - plane. ${\displaystyle m}$ ${\displaystyle x}$ ${\displaystyle y}$

The conical spiral can also be viewed as an orthogonal projection of the ground plan spiral onto the surface of the cone.

Examples

1) Assuming an Archimedean spiral , the conical spiral is obtained (see picture) ${\displaystyle \;r(\varphi )=a\varphi \;}$

${\displaystyle x=a\varphi \cos \varphi \ ,\qquad y=a\varphi \sin \varphi \ ,\qquad z=z_{0}+ma\varphi \ ,\quad \varphi \geq 0\ .}$

In this case, the conical spiral can also be understood as the intersection of a cone and a helical surface .

2) The second picture shows a conical spiral with a Fermat's spiral as a plan. ${\displaystyle \;r(\varphi )=\pm a{\sqrt {\varphi }}\;}$

3) The third example has a logarithmic spiral as a floor plan. It is characterized by a constant slope (see below). ${\displaystyle \;r(\varphi )=ae^{k\varphi }\;}$

4) In this example the floor plan is a hyperbolic spiral . It has an asymptote (black straight line). This asymptote is the outline of a hyperbola (purple), which the conical spiral for approximates. ${\displaystyle \;r(\varphi )=a/\varphi \;}$ ${\displaystyle \varphi \to 0}$

properties

Properties of conical spirals with outlines of the shape or are specified below: ${\displaystyle r=a\varphi ^{n}}$ ${\displaystyle r=ae^{k\varphi }}$

pitch

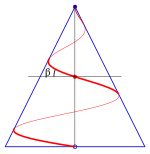
Pitch angle at one point of a conical spiral

The slope of a conical spiral is the slope of the spiral (tangent) relative to the horizontal ( - plane). The associated gradient angle is (see picture): ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle \beta }$

${\displaystyle \tan \beta ={\frac {z'}{\sqrt {(x')^{2}+(y')^{2}}}}={\frac {mr'}{\sqrt {(r')^{2}+r^{2}}}}\ .}$

For a spiral with : ${\displaystyle r=a\varphi ^{n}}$

• ${\displaystyle \tan \beta ={\frac {mn}{\sqrt {n^{2}+\varphi ^{2}}}}\ .}$

For an Archimedean spiral, and therefore the slope ${\displaystyle n=1}$ ${\displaystyle \ \tan \beta ={\tfrac {m}{\sqrt {1+\varphi ^{2}}}}\ .}$

• For a logarithmic spiral with is ( ). ${\displaystyle r=ae^{k\varphi }}$ ${\displaystyle \ \tan \beta ={\tfrac {mk}{\sqrt {1+k^{2}}}}\ }$ ${\displaystyle \color {red}{\text{ konstant!}}}$

A concho spiral is therefore also called an equiangular conical spiral.

Arc length

The length of an arc of a curve in a conical spiral is

${\displaystyle L=\int _{\varphi _{1}}^{\varphi _{2}}{\sqrt {(x')^{2}+(y')^{2}+(z')^{2}}}\,\mathrm {d} \varphi =\int _{\varphi _{1}}^{\varphi _{2}}{\sqrt {(1+m^{2})(r')^{2}+r^{2}}}\,\mathrm {d} \varphi \ .}$

For an Archimedean spiral, the occurring integral, as in the plane case, can be solved with the help of an integration table.

${\displaystyle L={\frac {a}{2}}{\big [}\varphi {\sqrt {(1+m^{2})+\varphi ^{2}}}+(1+m^{2})\ln {\big (}\varphi +{\sqrt {(1+m^{2})+\varphi ^{2}}}{\big )}{\big ]}_{\varphi _{1}}^{\varphi _{2}}\ .}$

For a logarithmic spiral, the integral can easily be solved:

${\displaystyle L={\frac {\sqrt {(1+m^{2})k^{2}+1}}{k}}(r{\big (}\varphi _{2})-r(\varphi _{1}){\big )}\ .}$

In other cases, elliptic integrals can occur.

completion

Development (green) of a conical spiral (red), right: side view. The settlement level is . At first it touches the cone in the purple straight line. ${\displaystyle \pi }$

For the development of a conical spiral, the distance between a curve point and the tip of the cone and the relationship between the angle and the angle in the development must be determined: ${\displaystyle \rho (\varphi )}$ ${\displaystyle (x,y,z)}$ ${\displaystyle (0,0,z_{0})}$ ${\displaystyle \varphi }$ ${\displaystyle \psi }$

${\displaystyle \rho ={\sqrt {x^{2}+y^{2}+(z-z_{0})^{2}}}={\sqrt {1+m^{2}}}\;r\ ,}$

${\displaystyle \varphi ={\sqrt {1+m^{2}}}\psi \ .}$

The polar representation of the developed conical spiral is:

• ${\displaystyle \rho (\psi )={\sqrt {1+m^{2}}}\;r({\sqrt {1+m^{2}}}\psi )}$

The development in the case is the curve in polar representation ${\displaystyle r=a\varphi ^{n}}$

${\displaystyle \rho =a{\sqrt {1+m^{2}}}^{\,n+1}\psi ^{n},}$

a coil of the same type. Specifically:

• If the outline of a conical spiral is an Archimedean spiral, the development is also an Archimedean spiral.

In the case of a hyperbolic spiral ( ), the development is even congruent to the floor plan. ${\displaystyle n=-1}$

In the case of a logarithmic spiral with , the development is the logarithmic spiral ${\displaystyle r=ae^{k\varphi }}$

${\displaystyle \rho =a{\sqrt {1+m^{2}}}\;e^{k{\sqrt {1+m^{2}}}\psi }\ .}$

Tangent track

Conical spiral with hyperbolic spiral as a floor plan: tangent track (purple circle). The black straight line is the asymptote of the hyperbolic spiral.

The intersection of the tangents of a conical spiral with the - plane (plane through the tip of the cone) is called the tangent track. ${\displaystyle x}$ ${\displaystyle y}$

For the conical spiral

${\displaystyle (r\cos \varphi ,r\sin \varphi ,mr)}$

is the tangent vector

${\displaystyle (r'\cos \varphi -r\sin \varphi ,r'\sin \varphi +r\cos \varphi ,mr')^{T}}$

and the tangent:

${\displaystyle x(t)=r\cos \varphi +t(r'\cos \varphi -r\sin \varphi )\ ,}$

${\displaystyle y(t)=r\sin \varphi +t(r'\sin \varphi +r\cos \varphi )\ ,}$

${\displaystyle z(t)=mr+tmr'\ .}$

The intersection of the tangent with the - plane has the parameter and is ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle t=-r/r'}$

• ${\displaystyle ({\frac {r^{2}}{r'}}\sin \varphi ,-{\frac {r^{2}}{r'}}\cos \varphi ,0)\ .}$

For is and the tangent track again a spiral, which, however, in the case (hyperbolic spiral) to a circle of radius degenerate (see picture). For is and the track again congruent to given logarithmic spiral spiral (for self-similarity of a logarithmic spiral ). ${\displaystyle r=a\varphi ^{n}}$ ${\displaystyle \ {\tfrac {r^{2}}{r'}}={\tfrac {a}{n}}\varphi ^{n+1}\ }$ ${\displaystyle n=-1}$ ${\displaystyle a}$ ${\displaystyle r=ae^{k\varphi }}$ ${\displaystyle \ {\tfrac {r^{2}}{r'}}={\tfrac {r}{k}}\ }$

Shells of two different marine snail species: on the left a left-handed shell Neptunea angulata , on the right a right-handed shell Neptunea despecta

Individual evidence

1. ^ New Scientist
2. ^ Conchospirals in the Flight of Insects
3. ↑ John D. Dyson: The Equiangular Spiral Antenna. In: IRE Transactions on Antennas and Propagation. Vol. 7, 1959, pp. 181-187.
4. ^ TA Kozlovskaya: The Concho-Spiral on the Cone. Vestn. Novosib. Gos. Univ., Ser. Mat. Mekh. Inform., 11: 2 (2011), 65-76.
5. ^ Siegmund Günther, Anton Edler von Braunmühl, Heinrich Wieleitner: History of mathematics. GJ Göschen, 1921, p. 92.
6. ↑ Theodor Schmid: Descriptive Geometry. Volume 2, Association of Scientific Publishers, 1921, p. 229.

Web links

• Jamnitzer gallery: 3D spirals. (Access denied).
• Eric W. Weisstein : Conical Spiral . In: MathWorld (English).