Fermatsche spiral

Fermatsche spiral: a branch

Fermatsche spiral: both branches

A Fermatsche or parabolic spiral is a flat curve named after Pierre de Fermat , which is expressed in polar coordinates by the equation

${\displaystyle r=\pm a{\sqrt {\varphi }}\ ,\ \varphi \geq 0}$

a parabola (with a horizontal axis) can be described.

The Fermatian spiral looks similar to the Archimedean spiral . In contrast to it, however, it has decreasing winding spacing, i. That is, the turns are always closer to the outside.

Like other spirals, Fermat's spirals are also used to construct continuous curvature transition curves.

Description in Cartesian coordinates

The Fermat spiral with the polar equation

${\displaystyle r=a{\sqrt {\varphi }}\ ,\quad \varphi \geq 0}$

can be in Cartesian coordinates through the parametric representation ${\displaystyle (x=r\cos \varphi ,\;y=r\sin \varphi )}$

• ${\displaystyle x=a{\sqrt {\varphi }}\cos \varphi ,\qquad y=a{\sqrt {\varphi }}\sin \varphi ,\quad \varphi \geq 0}$

describe.

The parameter representation and results in a representation with an equation: ${\displaystyle \ \varphi ={\tfrac {r^{2}}{a^{2}}},\ r={\sqrt {x^{2}+y^{2}}}\ }$

• ${\displaystyle {\frac {y}{x}}=\tan {\big (}{\frac {x^{2}+y^{2}}{a^{2}}}{\big )}\ .}$

properties

Decomposition of the plane

A Fermat's spiral divides the plane into two connected areas (here black and white)

A complete Fermat's spiral (both branches) is, in contrast to an Archimedean or hyperbolic spiral, a smooth, colon-free curve that divides the plane, like a straight line or a circle or a parabola, into two connected areas. The particular challenge when dividing the plane using a Fermat spiral is that it is not as easy with the naked eye to decide on which side of the curve a point is located as with a straight line, circle or parabola.

curvature

With the formula

${\displaystyle \kappa ={\frac {r^{2}+2(r')^{2}-r\;r''}{(r^{2}+(r')^{2})^{3/2}}}}$

for the curvature of a curve in polar representation and the derivatives and the Fermat's spiral results for the curvature ${\displaystyle \;r=r(\varphi )\;}$ ${\displaystyle \;r'={\tfrac {a}{2{\sqrt {\varphi }}}}={\tfrac {a^{2}}{2r}}\;}$ ${\displaystyle \;r''=-{\tfrac {a}{4{\sqrt {\varphi }}^{3}}}=-{\tfrac {a^{4}}{4r^{3}}}\;}$

• ${\displaystyle \kappa (r)={\frac {2r(4r^{4}+3a^{4})}{(4r^{4}+a^{2})^{3/2}}}.}$

The curvature is at the zero point . So the complete spiral has ${\displaystyle 0}$

• a turning point at the zero point with the x-axis as a turning tangent.

The inversion of a Fermat's spiral (green) on the unit circle (red) results in a lituus spiral (blue)

inversion

The reflection on the unit circle (inversion) can be described in polar coordinates by . ${\displaystyle \ (r,\varphi )\mapsto ({\tfrac {1}{r}},\varphi )\ }$

• The image of the Fermat's spiral when reflected on the unit circle is a lituus spiral with . ${\displaystyle \ r=a{\sqrt {\varphi }}\ }$ ${\displaystyle \;r={\frac {1}{a{\sqrt {\varphi }}}}\;}$

For both curves intersect at a fixed point on the unit circle. ${\displaystyle \;\varphi ={\tfrac {1}{a^{2}}}\;}$

• The turning tangent ( axis) of the Fermat spiral (at the zero point) merges with the reflection and is the asymptote of the lituus spiral. ${\displaystyle x}$

Area between curves

The sector area for the curve between and is ${\displaystyle \;r(\varphi _{1}),\varphi _{1})\;}$ ${\displaystyle \;(r(\varphi _{2}),\varphi _{2})\;}$

${\displaystyle {\underline {A}}={\tfrac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}r(\varphi )^{2}\;d\varphi ={\tfrac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}a^{2}\varphi \;d\varphi ={\frac {a^{2}}{4}}{\big (}\varphi _{2}^{2}-\varphi _{1}^{2}{\big )}}$

${\displaystyle \quad ={\frac {a^{2}}{4}}{\big (}\varphi _{2}+\varphi _{1}{\big )}{\big (}\varphi _{2}-\varphi _{1}{\big )}\;.}$

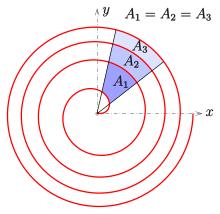
Fermatsche spiral: surfaces between curved arcs

If you increase both angles by , the result is ${\displaystyle 2\pi }$

${\displaystyle {\overline {A}}={\frac {a^{2}}{4}}{\big (}\varphi _{2}+\varphi _{1}+4\pi {\big )}{\big (}\varphi _{2}-\varphi _{1}{\big )}={\underline {A}}+a^{2}\pi {\big (}\varphi _{2}-\varphi _{1}{\big )}\;.}$

So the content of the sector area between the curves is ${\displaystyle A}$

• ${\displaystyle A=a^{2}\pi {\big (}\varphi _{2}-\varphi _{1}{\big )}\;.}$

${\displaystyle A}$depends only on the difference between the two angles and not on the angles themselves.

In the example (see picture) have so all adjacent sector Strip same content: . ${\displaystyle A_{1}=A_{2}=A_{3}}$

This property of the Fermat spiral plays a role in electrical engineering in the manufacture of variable capacitors .

The intermediate areas (white, blue, yellow) all have the area of ​​the circle drawn

Special case of Fermat

In 1636 Fermat reported the following special case in a letter to Marin Mersenne :

Be there . Then the content of the black area (see picture) is half the area of ​​the circle with radius . The intermediate surfaces (white, blue, yellow) have the following content : ${\displaystyle \varphi _{1}=0,\varphi _{2}=2\pi }$ ${\displaystyle A_{0}=a^{2}\pi ^{2}=}$ ${\displaystyle K_{0}}$ ${\displaystyle r(2\pi )}$ ${\displaystyle A={\color {red}2}a^{2}\pi ^{2}}$

• The area between two spiral arcs after a complete circling is equal to the area of ​​the circle . ${\displaystyle K_{0}}$

Arc length

The length of the arc of a Fermat's spiral between two points can be calculated using the formula for curves in polar representation : ${\displaystyle \;(r(\varphi _{1}),\varphi _{1}),(r(\varphi _{2}),\varphi _{2})\;}$

${\displaystyle L=\int \limits _{\varphi _{1}}^{\varphi _{2}}{\sqrt {\left(r^{\prime }(\varphi )\right)^{2}+r^{2}(\varphi )}}\,\mathrm {d} \varphi =\cdots ={\frac {a}{2}}\int \limits _{\varphi _{1}}^{\varphi _{2}}{\sqrt {{\frac {1}{\varphi }}+4\varphi }}\,\mathrm {d} \varphi \;.}$

The solution of this integral is only possible numerically or with the help of an elliptic integral .

Individual evidence

1. ↑ Anastasios M. Lekkas1, Andreas R. Dahl, Morten Breivik, Thor I. Fossen4: Continuous-Curvature Path GenerationUsing Fermat's Spiral. In: Modeling, Identification and Control. Vol. 34, No. 4, 2013, pp. 183-198, ISSN  1890-1328 .
2. ^ Fritz Wicke: Introduction to higher mathematics. Springer-Verlag, 2013, ISBN 978-3-662-36804-6 , p. 414.
3. ↑ Lettre de Fermat à Mersenne du 3 June 1636, dans Paul Tannery. In: Oeuvres de Fermat. T. III, p. 277, Lire en ligne.

literature

• Friedrich Grelle : Analytical Geometry of the Plane , Verlag F. Brecke, 1861 [1] , p. 213.
• Jac. Phil Kulik : Spiral Lines in Textbook of Higher Analysis, Volume 2 , In Commiss. at Kronberger u. Rziwnatz, 1844, [2] , p. 226.

Web links

• Eric W. Weisstein : Fermat's Spiral . In: MathWorld (English).
• Mathcurve: Fermatsche spiral