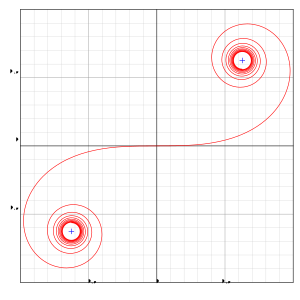
Clothoid
The clothoid also clothoid (from Greek κλώθω spinning, '), is a special plane curve . Except for similarity, it is uniquely determined in the plane by the property that the curvature at every point on the curve is proportional to the length of its arc up to the point. Other names for the clothoid are Cornu spiral (after Marie Alfred Cornu ) and spinning curve (since the graph that runs from one point of convergence to another resembles a spool of thread that is "wound around").
The equations of the clothoid were first recorded in 1694 by Jakob I Bernoulli . But it was neither drawn nor numerically calculated by him. This was done by Leonhard Euler in 1743 when he rediscovered the equations while studying spirally coiled coil springs. However, he did not succeed in determining the asymptotic endpoints until 1781. In 1874, the equations were discovered and examined again independently by the French physicist Alfred Cornu during diffraction calculations. In Anglo-Saxon literature it is therefore usually referred to as the Euler (Cornu) spiral .
In 1937 the clothoid was first used by Leopold Oerley as a geometric element in road construction, and from 1938 the motorway engineer Hans Lorenz used it consistently when planning the Reichsautobahn Vienna – Brno – Wroclaw . In 1954 the clothoid was made accessible to the general public with a comprehensive set of tables (Kasper, Schürba, Lorenz: Die Klotoide as a routing element, see literature ) for routing and staking out work. In this table work, clothotids (without "h") are written throughout . The old editions of the Taschenbuch der Mathematik (Bronstein-Semendjajew) also prefer this notation. The spelling according to Duden is clothoid.
The clothoid is used as a transition curve in curves in road construction and railway construction. Their curvature increases linearly, which means that instead of an abrupt jerk, there is a gradual acceleration transition from driving straight ahead to driving in a circle .
In today's routing and CAD programs, the numerical calculation of clothoids is integrated in the program library and takes place automatically.
Clothoid equation
The radius of curvature of this curve is or should be: inversely proportional to the length of its curve, formally expressed with the capital letter convention in the road building standards:
where the radius of curvature, the length of the curve arc from the fixed curve starting point to the curve point under consideration and any, but fixed, positive, real constant denotes. This constant is called the clothoid parameter .
The clothoid equation clearly follows from this requirement if one specifies a starting point and an initial slope. This is in parametric form with a starting point and initial slope by parameterized:
where then the length of the curve is from to . Thus applies to the curvature of this curve
- .
It also has the two asymptotic points and .
Unit clothoid
The unit clothoid is a clothoid with the parameter . The basic equation shows that the parameter is a characteristic quantity. The Einheitsklothoide was used to set up at tables for the calculation of points on the clothoid, analogous to the board works for trigonometric functions, which the unit circle with underlying. The values taken there for the coordinates of the points on the clothoid are multiplied by the given parameter , since all clothoids are similar to one another and can be proportionally enlarged or reduced.
Well-known, frequently used tables were (see also literature ):
- The Klotoids as a routing element by Kasper, Schürba, Lorenz
- Clothoid paperback for design and staking out by Krenz, Osterloh
Designations according to Kasper, Schürba, Lorenz:
| Parameters of the clothoid | |
| Radius of curvature in the considered end point of the clothoid section (i.e. also the minimum radius of curvature of the clothoid section) | |
| Length of the clothoid section | |
| Angle of intersection of the tangents at the start and end point in radians |
The table values and relate to the tangent at the origin (the only point of inflection) of the clothoid (0,0) with the radius of curvature of " infinite ". The X-coordinate is the section on this tangent, the Y-coordinate is the orthogonal distance of the clothoid point from the tangent. Input value is .
In order to simplify clothoid calculations with mechanical calculators, which only allowed the four basic arithmetic operations, special tables for frequently occurring tasks were added in order to keep the calculation effort within limits.
Modern calculation methods
Today neither tables nor approximate solutions are required for clothoid calculations. Clothoids are particularly well suited for a program-controlled calculation because the formulas are simple, require little programming effort and have very good runtime behavior. Because of the very frequent use of clothoids in the alignment of traffic routes, the calculation process is used as an example.
Basic equations:
Instead of the sine or cosine function, their power series expansions are used for the calculation
used and integrated. If you then substitute for again , you get the following very simple series expansion for the coordinates and on the original tangent :
For the clothoid section used in the area of routing calculations , the maximum value is 0.5. In order to be prepared for rare special cases, the program should allow T values up to π (3.14159) so that the same angle of rotation (180 °) is covered as in a semicircle. The series elements for and converge to zero after just a few steps. Because the factorial function is in the denominator, its value grows rapidly. When the value decreases the counter and also accelerates the calculation. The accuracy of the calculation can be controlled via a limit value that leads to the abortion of the calculation. An accuracy that has five valid decimal places is usual when calculating with 8 bytes of data width ( double precision ). For graphics output, an accuracy is sufficient that corresponds to half the pixel diameter of the output device, multiplied by the reciprocal scale factor (reason: see Bresenham algorithm ).
In order to transfer the local coordinates and into the higher-level reference system, a simple transformation , e.g. B. necessary via already known coordinates of the start and end point in the reference system. The calculation of clothoid points is just as easy when using computers today as it is for points on the alignment elements of straight lines and arcs.
Application in optics
Under diffraction which is usually Fraunhofer diffraction understood, are mapped at the radiation from infinity (parallel rays) by lenses to a finite level. In contrast, Fresnel diffraction describes diffraction phenomena in the near field. Both forms of diffraction are two borderline cases of Kirchhoff's diffraction integral . For example, the Fresnel integrals and the intensity of the light distribution behind an illuminated edge describe with any real parameter :
- .
Definition of the clothoid using Fresnel integrals
Together, the previous two equations also allow a parametric representation
a clothoid. If you choose , you get the clothoid with it .
- The two convergence points are at the coordinates (z, z) and (−z, −z) with
- The length of a curve arc of the clothoid, parameterized by and measured from the origin , is
The length of the curve is therefore unlimited. And we see that the differential geometricians describe the clothoid in such a way that the curve length is always equal to its free parameter. This is then generally called the natural curve parameterization for any continuous curve.
- The curvature (its reciprocal value is the radius of curvature ) is proportional to the length of the curve arc from the point (0,0).
Furthermore, we now also recognize the connection with “ the road builder” .
If one chooses only the first term of its Taylor series for a first approximation of the curve at the origin, one obtains
so what a cubic parabola represents.
Application in traffic route construction
In traffic route construction, the clothoid is used as a transition element between two straight lines, or generally two elements with constant but different curvature, when calculating the alignment of a traffic axis. It is used on numerous sections of road and rail routes.
Clothoid as a routing element
The design speed , from which the minimum radii or, in the case of clothoids, minimum parameters result, is used to dimension the routing elements in a dynamic vehicle routing of traffic routes . The design speed depends, among other things, on the importance of a traffic route, i.e. high for long-distance connections and lower for regional connections. A low design speed allows a route that can be better adapted to the topographical conditions. Traffic volume must also be taken into account. Urban streets, on the other hand, are usually not routed dynamically or planned at a low design speed.
A route is composed on the one hand of routing elements with constant curvature such as straight lines and circular arcs, on the other hand of clothoids as transition arcs with increasing and decreasing curvature. The curvature increases or decreases linearly with the length on the clothoid.
The following speaks in favor of using the clothoid as a transition between elements with constant curvature in road construction:
- When cornering, the steering wheel must be turned to steer the vehicle into the curve. At a constant driving speed and a uniform change in the steering angle, the vehicle moves on a line that corresponds approximately to a clothoid. The clothoid as a transition element ensures that the driver is not forced to make an abrupt steering maneuver, but that the lateral acceleration increases or decreases linearly.
- The drainage of the road surface when it rains requires that the road surface be inclined in the transverse direction ( transverse slope ) in order to prevent aquaplaning . A transverse slope of the roadway is also necessary in order to limit the lateral acceleration to an acceptable level. If the road is sloping, the vertical acceleration due to gravity (9.81 m / s²) acts against it and the forces are better transferred to the road. In the case of curves, the edges of the road are rotated around the axis of the road so that the outer edge is higher and the inner edge is lower than the axis. This “twisting” of the road around the axis requires a certain transition length. The clothoid as a transition curve when there is a change in curvature ensures that the transition can be created linearly within the length of this element.
- The clothoid improves the visual alignment of a route. The driver of a vehicle perceives the roadway from a perspective which, viewed in the direction of travel, leads to a significant shortening of the longitudinal development. Without a transition curve, a change in curvature acts like a kink in the axis. The clothoid as a transition curve ensures that a curve is better perceived and thus correctly steered.
With railway lines, transition bends have the same advantages. Rail-bound vehicles are controlled under pressure and have no tolerance in the transverse direction. In this case, a change in curvature without a transition curve creates a sudden change in the transverse acceleration that is quickly perceived as uncomfortable. To make matters worse, an abrupt change of curvature causes increased wear on the rails and the wheelsets. However, there are minor deviations from the execution in road construction:
- In the case of rails, the drainage of the driveway does not have to be taken into account. In a straight line, both rails are at the same height. In curves, only the outer rail is raised to counteract the lateral acceleration. This type of execution is known as " cant ". The transition curve ensures that the elevation can be linear within its length.
- In railway construction at conventional speeds (<160 km / h), cubic parabolas ( bare arcs ) are still used as transition arcs, which have a course similar to the clothoids in the vicinity of the origin.
In roller coasters , also rail-bound vehicles, clothoids are used so that the passengers are not burdened by strong lateral acceleration. In the case of the roller coaster, the speed in each section of the route is known with minor deviations; thus the acting transverse forces can be almost completely eliminated by adjusting the elevation of the curves. The prerequisite for this are transition bends.
In the case of lift supports in cable car systems, the roller batteries are often built in a clothoid shape in order to offer the passengers of the lift system a higher level of comfort.
Calculation of an axis with clothoids as transition elements
In order to define the position of the axis of a traffic route, work is carried out in two stages:
- During the design planning, the main elements of the axis are determined (main point calculation). The result is an axis that fits into the planning corridor and meets the design guidelines (design speed, etc.). The length of the axis results from the sum of the lengths of the axis elements. A “station” is assigned to each main point of the axis, the summed lengths from the start of the axis to the respective main point. The "stationing" of the elements (from station / to station) creates a clear assignment within the axis.
- For construction work, the sequence of points on the axis is condensed in the course of the implementation planning to such an extent that staking out and construction according to the plan is guaranteed (axis minor point calculation).
The determination of the position of a clothoid as an axis element in the reference coordinate system takes place during the axis principal point calculation. In the case of clothoids, boundary conditions must be observed. The simplest case, the element sequence straight line - clothoid - circular arc - clothoid - straight line , should serve as an example:
- The center of the circular arc is no longer at a distance (radius) perpendicular to the straight line. The clothoids cause the arc to move away from the straight line, which is denoted by. The distance from the center of the circle is therefore . results from the end point of the clothoid via the center point coordinates of the circular arc, based on the original tangent of the clothoid:
Distance from the origin of the clothoids orthogonal distance from the origin tangent Moving away from the original tangent
- The angle of intersection of the two straight lines must be greater than the sum of the angles of rotation of both clothoids. The parameters in road construction vary in range . The minimum required for = per clothoid is 3.54 gon or 3.18 °, a maximum of 31.83 gon or 28.65 ° is required per clothoid. If the cutting angle is smaller, there will be overlaps in the area of the circular arc. If the cutting angle exactly meets the minimum conditions for the angle of rotation of the two clothoids, the length of the circular arc is zero. One then speaks of a vertex clothoid. This construction should be avoided when laying out the route.
- The end point of the initial straight line or the starting point of the final straight line results from the plumb point of the center of the circle on the straight line - in this case identical to the original tangent - minus the distance . In this case too, there may be overlaps with neighboring elements that connect to both straight lines.
In the case of transitions between two circular arcs, the distance between the two circle centers is determined by calculating the distance between two cases:
- The connection of circular arcs with opposite curvature creates a turning clothoid with two branches. The parameters of the two clothoid branches can be different, but they always have a common origin with the same tangent slope.
- The connection of circular arcs that are curved in the same direction creates an ovoid , i.e. a clothoid section that begins with the radius of the first circular arc and ends with the radius of the second circular arc. In this case, the origin of the clothoid is not on the axis.
If the distances depending on the clothoid parameters are taken into account when calculating the basic elements straight line and circular arc , the clothoids can then be precisely inserted using simple transformations.
In the case of clothoids, however, it must be taken into account that they cannot be offset parallel when the axis is shifted, as is possible at any time with straight lines and arcs. Changing the parameters does not create a line that strictly conforms to the conditions of parallelism. However, the deviations in short clothoid sections, as they are mainly used in the routing, are regularly so small that the shortfall is within the building tolerance. However, this must always be checked mathematically and, if necessary, remedied by an auxiliary construction.
Identification points of the clothoid and limits of use
All clothoids have a geometric similarity, which means that the same directional angle and the same ratio value always occurs at a certain point in the shape of a clothoid . Certain integer ratio values (with the exception of the value of 1.5) are used as characteristic points designated the clothoid. For example, the point at which is called as code point 1.
When using the clothoids in the routing, it must be noted that there are certain application limits for clothoids. For reasons of driving dynamics, a clothoid should only be used between identification points 3 and 1. If you choose a code greater than 3, the change in direction at the beginning of the clothoid is too small and the vehicle driver may steer too late. When using an identification point smaller than 1, there is a risk that the vehicle driver can no longer follow the curve and deviates from the road (principle of the dog curve ). These considerations result in the following formulas for the application limits of the clothoids:
| Minimum value for clothoid parameters | |
| Maximum value for clothoid parameters |
Graphic representation of an axis
Site plan and elevation plan are the most important planning documents to represent a route. Since the course of the curvature is also very important for many planning decisions, it is shown as a curvature band in the profile view below the height display .
The horizontal axis of the curvature band corresponds to the axis length as in the height display ( gradient ). The elements are applied to this axis according to their station (see above). The curvature of a straight line is zero and lies on the axis. Circular arcs have a constant curvature , their line of curvature lies above the axis for right-hand arcs (positive radius) and below the axis for left-hand arcs (negative radius). Depending on the space on the plan and the size of the radii, the curvature of the axial elements is multiplied by a constant factor that is selected so that the result is a clear representation. The curvature line is drawn at the distance to the axis determined in this way. Clothoids, the curvature of which increases or decreases linearly with the length of the element, form the inclined ramps between the straight and circular elements in the band of curvature.
The " curvature " can be seen from the curvature band , ie the course of curvature in the course of an axis. The transverse slope of the carriageway is shown as a transverse slope parallel to and below the curvature band. The transverse slope, which depends on the radius of an element due to the lateral acceleration, can be clearly planned and displayed in this way. Changes in bank slope are regularly within the clothoid sections, but they have to be coordinated very precisely with the gradient from a drainage point of view so that functioning drainage of the roadway is guaranteed.
literature
- Günter Weise, Walter Durth u. a .: Road construction planning and design . Verlag für Bauwesen, Berlin 1997, ISBN 3-345-00579-4 .
- Hugo Kasper, Walter Schürba, Hans Lorenz: The Klotoide as a routing element . Ferd. Dümmlers Verlag, Bonn 1954, DNB 452330076 .
- Günter Wolf: Road planning . Werner Verlag, 2005, ISBN 3-8041-5003-9 .
- Alfred Krenz, Horst Osterloh: Clothoid paperback for design and staking out . 14th edition, 48-50. Th. Bauverlag, Wiesbaden, Berlin 1981, ISBN 3-7625-1273-6 .
Web links
- Route planning
- Driving dynamics
- The Euler / Cornu spiral, Clothoid ( Memento from June 20, 2010 in the Internet Archive )
Individual evidence
- ^ Raymond Clare Archibald : Euler Integrals and Euler's Spiral - Sometimes called Fresnel Integrals and the Clothoide or Cornu's Spiral. In: American Math Monthly. Volume 25, 1918, pp. 276-282 (online).
- ↑ Michael Hinterseher: Development of concepts, algorithms and optimization methods for the transformation of nodes in a network, taking into account integrity conditions . Munich 1999, chap. 1.1: Historical background ( online [accessed January 7, 2013]).