Bresenham's algorithm

The Bresenham algorithm is an algorithm used in computer graphics for drawing ( rasterizing ) straight lines or circles on raster displays . There is a separate overview article for line algorithms, the concrete implementation is explained here.

The algorithm was developed in 1962 by Jack Bresenham , then a programmer at IBM . The special thing about his algorithm is that it minimizes rounding errors that arise from the discretization of continuous coordinates, and at the same time is easy to implement, with the addition of whole numbers as the most complex operation, and thus without multiplication, division and floating point numbers .

With a slight extension, the original algorithm, which was designed for straight lines, can also be used for the rasterization of circles . Even the square terms that occur in the circle can be derived recursively without any multiplication from the respective preceding term , whereby the term does not count as a multiplication, since it is implemented in hardware or at the assembly level as a simple shift operation and the term im Ultimately, it can be avoided entirely. ${\displaystyle (n+1)^{2}=n^{2}+2\cdot n+1}$ ${\displaystyle 2\cdot n}$ ${\displaystyle n^{2}}$

Due to the above properties, the importance of the Bresenham algorithm has remained unbroken to this day, and it is used in plotters , in the graphics chips of modern graphics cards and in many graphics libraries , among other things . It is so simple that it is not only used in the firmware of such devices, but can also be implemented directly in hardware in graphics chips.

The name “Bresenham” is also used today for a whole family of algorithms that were actually developed later by others, but in the successor of Bresenham and with a related approach. See further references below.

approach

Rasterization of a line according to the Bresenham method, below the course of the error variables

The variant presented here is a very practical approach and was first published by Pitteway and verified by van Aken . Below the variant is compared with the original formulation by Bresenham and it is shown that the solutions are equivalent.

To understand the algorithm, one restricts oneself to the first octant , i.e. a line with a slope between 0 and 1 from to . Be and with . For other octants, case distinctions have to be made later using the signs of and and the reversal of roles of and . ${\displaystyle (x_{\mathrm {start} },y_{\mathrm {start} })}$ ${\displaystyle (x_{\mathrm {end} },y_{\mathrm {end} })}$ ${\displaystyle dx=x_{\mathrm {end} }-x_{\mathrm {start} }}$ ${\displaystyle dy=y_{\mathrm {end} }-y_{\mathrm {start} }}$ ${\displaystyle 0<dy\leq dx}$ ${\displaystyle dx}$ ${\displaystyle dy}$ ${\displaystyle x}$ ${\displaystyle y}$

The algorithm then runs in such a way that you always take a step in the "fast" direction (here the positive direction) and, depending on the incline, every now and then an additional step in the "slower" direction (here ). One uses an error variable, which gets the (smaller) value subtracted with a step in the direction . If the value falls below zero, a step is due and the (larger) value is added to the error variable. These repeated “crossover” subtractions and additions resolve the division of the slope triangle into more elementary calculation steps. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle dy}$ ${\displaystyle y}$ ${\displaystyle dx}$ ${\displaystyle m=dy/dx}$

In addition, this error element must be sensibly initialized beforehand. To do this, consider the case of , in which there should be a step in the middle (after half of ) . So you initialize the error term with . (Whether it is rounded up or down to a whole number hardly matters.) ${\displaystyle dy=1}$ ${\displaystyle dx}$ ${\displaystyle y}$ ${\displaystyle (dx/2)}$

From a mathematical point of view, the straight line equation

${\displaystyle y=y_{\mathrm {start} }+(x-x_{\mathrm {start} })\cdot {\frac {dy}{dx}}}$

dissolved in

${\displaystyle 0=dx\cdot (y-y_{\mathrm {start} })-dy\cdot (x-x_{\mathrm {start} })}$

and the zero on the left is replaced by the error term. A step by 1 in -direction (variable ) causes the error term to be reduced by . If the error element gets below zero, it is increased by a step by 1 in the direction (variable ) , which according to the prerequisite makes the error element positive again in any case, or at least brings it to zero. ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle 1\cdot dy}$ ${\displaystyle y}$ ${\displaystyle y}$ ${\displaystyle 1\cdot dx}$ ${\displaystyle dx>=dy}$

The original approach according to Bresenham (see below) proceeds more geometrically, whereby an additional factor 2 is included in its iteration formulas on both sides (except for the error element) and the error element initialization is also derived differently.

Easy implementation

A first implementation is not very elegant, but demonstrates the principle of the algorithm very well.

 REM Bresenham-Algorithmus für eine Linie im ersten Oktanten in Pseudo-Basic
 dx = xend-xstart
 dy = yend-ystart
 REM im ersten Oktanten muss 0 < dy <= dx sein

 REM Initialisierungen
 x = xstart
 y = ystart
 SETPIXEL x,y
 fehler = dx/2

 REM Pixelschleife: immer ein Schritt in schnelle Richtung, hin und wieder auch einer in langsame
 WHILE x < xend
    REM Schritt in schnelle Richtung
    x = x + 1
    fehler = fehler - dy
    IF fehler < 0 THEN
       REM Schritt in langsame Richtung
       y = y + 1
       fehler = fehler + dx
    END IF
    SETPIXEL x,y
 WEND

Comparison with the original Bresenham formulation

 REM Quasi-Bresenham-Algorithmus     REM Original-Bresenham
 dx = xend-xstart                    dx = xend-xstart
 dy = yend-ystart                    dy = yend-ystart

                                     d = 2*dy – dx
                                     dO = 2*dy
                                     dNO = 2*(dy - dx)

 x = xstart                          x = xstart
 y = ystart                          y = ystart
 SETPIXEL x,y                        SETPIXEL x,y
 fehler = dx/2                       fehler = d

 WHILE x < xend                      WHILE x < xend
    x = x + 1                           x = x + 1
    fehler = fehler-dy
    IF fehler < 0 THEN                  IF fehler <= 0 THEN
                                           fehler = fehler + dO
                                        ELSE
       y = y + 1                           y = y + 1
       fehler = fehler + dx                fehler = fehler + dNO
    END IF                              END IF
    SETPIXEL x,y                        SETPIXEL x,y
 WEND                                WEND

Apart from the adaptation to the BASIC dialect used, the following differences in the original formulation must be observed:

• The error term is used with the opposite sign.
• The sign of the error element is queried before it is updated, which means that additional initialization with the dy term is necessary.
• The error element is expanded by a factor of 2, so that no division by 2 takes place during initialization, but the step variables for the error updates are twice as large.

If one takes these differences in the formulation into account, it turns out that both formulations work identically and are therefore equivalent.

More elegant implementations

The source code of a BASIC program and then a subroutine in C , which do not have to expressly differentiate between cases in eight octants, follow as more elegantly formulated examples .

The algorithm should be valid for all octants. The signs of the coordinate distances and the possible interchanging of the roles of x and y must be taken into account. If one were to make these case distinctions within the innermost loop , i.e. in large numbers, this would significantly reduce the speed of the calculations. An efficient solution attempts to process all these case distinctions in the initialization phase of the method before the inner main loop, so that only the one query for the Bresenham error element still has to be made within the inner loop.

This formulation introduces various abstractions (as Stockton indirectly suggested): First, the step in the fast direction is now viewed as a parallel step (parallel to a coordinate axis), and if there is also a step in the slow direction, it becomes a diagonal step . Then you can determine variable values ​​in the initialization, which specify the step sizes in the two coordinate directions in advance for these cases and thus achieve the generalization for the eight octants. For example, in the case of a parallel step, the step size in the direction perpendicular to it is precisely zero. Second, the error term continues to be calculated as in the first octant, with absolute values ​​of the distances. In the innermost loop, the step in the fast direction is no longer carried out first, but the error term is updated first, and only then are the step sizes added to the previous coordinates, depending on whether a parallel or a diagonal step is required:

BASIC implementation

 REM Bresenham-Algorithmus für eine Linie in einem beliebigen Oktanten in Pseudo-Basic
 dx = xend-xstart
 dy = yend-ystart

 REM Initialisierungen
 adx = ABS(dx): ady = ABS(dy) ' Absolutbeträge Distanzen
 sdx = SGN(dx): sdy = SGN(dy) ' Signum der Distanzen

 IF adx > ady THEN
   ' x ist schnelle Richtung
   pdx = sdx: pdy = 0   ' pd. ist Parallelschritt
   ddx = sdx: ddy = sdy ' dd. ist Diagonalschritt
   deltaslowdirection  = ady: deltafastdirection  = adx ' Delta in langsamer Richtung, Delta in schneller Richtung
 ELSE
   ' y ist schnelle Richtung
   pdx = 0  : pdy = sdy ' pd. ist Parallelschritt
   ddx = sdx: ddy = sdy ' dd. ist Diagonalschritt
   deltaslowdirection  = adx: deltafastdirection  = ady ' Delta in langsamer Richtung, Delta in schneller Richtung
 END IF

 x = xstart
 y = ystart
 SETPIXEL x,y
 fehler = deltafastdirection/2

 REM Pixelschleife: immer ein Schritt in schnelle Richtung, hin und wieder auch einer in langsame
 FOR i=1 TO deltafastdirection          ' Anzahl der zu zeichnenden Pixel
    REM Aktualisierung Fehlerterm
    fehler = fehler - deltaslowdirection
    IF fehler < 0 THEN
       fehler = fehler + deltafastdirection ' Fehlerterm wieder positiv machen
       REM Schritt in langsame Richtung
       x = x + ddx: y = y + ddy ' Diagonalschritt
    ELSE
       REM Schritt in schnelle Richtung
       x = x + pdx: y = y + pdy ' Parallelschritt
    END IF
    SETPIXEL x,y
 NEXT

C implementation

In this implementation use is made of the signum function .

/* signum function */
int sgn(int x){
  return (x > 0) ? 1 : (x < 0) ? -1 : 0;
}

void gbham(int xstart,int ystart,int xend,int yend)
/*--------------------------------------------------------------
 * Bresenham-Algorithmus: Linien auf Rastergeräten zeichnen
 *
 * Eingabeparameter:
 *    int xstart, ystart        = Koordinaten des Startpunkts
 *    int xend, yend            = Koordinaten des Endpunkts
 *
 * Ausgabe:
 *    void SetPixel(int x, int y) setze ein Pixel in der Grafik
 *         (wird in dieser oder aehnlicher Form vorausgesetzt)
 *---------------------------------------------------------------
 */
{
    int x, y, t, dx, dy, incx, incy, pdx, pdy, ddx, ddy, deltaslowdirection, deltafastdirection, err;

/* Entfernung in beiden Dimensionen berechnen */
   dx = xend - xstart;
   dy = yend - ystart;

/* Vorzeichen des Inkrements bestimmen */
   incx = sgn(dx);
   incy = sgn(dy);
   if(dx<0) dx = -dx;
   if(dy<0) dy = -dy;

/* feststellen, welche Entfernung größer ist */
   if (dx>dy)
   {
      /* x ist schnelle Richtung */
      pdx=incx; pdy=0;    /* pd. ist Parallelschritt */
      ddx=incx; ddy=incy; /* dd. ist Diagonalschritt */
      deltaslowdirection =dy;   deltafastdirection =dx;   /* Delta in langsamer Richtung, Delta in schneller Richtung */
   } else
   {
      /* y ist schnelle Richtung */
      pdx=0;    pdy=incy; /* pd. ist Parallelschritt */
      ddx=incx; ddy=incy; /* dd. ist Diagonalschritt */
      deltaslowdirection =dx;   deltafastdirection =dy;   /* Delta in langsamer Richtung, Delta in schneller Richtung */
   }

/* Initialisierungen vor Schleifenbeginn */
   x = xstart;
   y = ystart;
   err = deltafastdirection/2;
   SetPixel(x,y);

/* Pixel berechnen */
   for(t=0; t<deltafastdirection; ++t) /* t zaehlt die Pixel, deltafastdirection ist Anzahl der Schritte */
   {
      /* Aktualisierung Fehlerterm */
      err -= deltaslowdirection;
      if(err<0)
      {
          /* Fehlerterm wieder positiv (>=0) machen */
          err += deltafastdirection;
          /* Schritt in langsame Richtung, Diagonalschritt */
          x += ddx;
          y += ddy;
      } else
      {
          /* Schritt in schnelle Richtung, Parallelschritt */
          x += pdx;
          y += pdy;
      }
      SetPixel(x,y);
   }
} /* gbham() */

Compact variant

The Bresenham algorithm can also be implemented in a simple variant in C:

void line(int x0, int y0, int x1, int y1)
{
  int dx =  abs(x1-x0), sx = x0<x1 ? 1 : -1;
  int dy = -abs(y1-y0), sy = y0<y1 ? 1 : -1;
  int err = dx+dy, e2; /* error value e_xy */

  while (1) {
    setPixel(x0,y0);
    if (x0==x1 && y0==y1) break;
    e2 = 2*err;
    if (e2 > dy) { err += dy; x0 += sx; } /* e_xy+e_x > 0 */
    if (e2 < dx) { err += dx; y0 += sy; } /* e_xy+e_y < 0 */
  }
}

The error element is used as step recognition for both the slow and the fast direction. The four quadrants are covered by the sign increment (sx, sy). The accumulation of the error element triggers the conditional step when the threshold value is exceeded, in contrast to the original variant simultaneously in both directions: positive error values ​​for x and negative for the y-axis. The example elegantly shows the xy symmetry of the Bresenham algorithm.

Circular variant of the algorithm

Scanning a circular line according to the Bresenham method

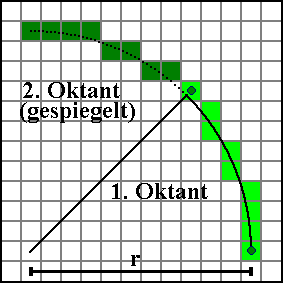
The approach for the circular variant of the Bresenham algorithm does not go back to Bresenham himself, it is similar to Horn's method from the review article , see also Pitteway and van Aken below. One starts accordingly from the circular equation . At first only the first octant is considered. Here you want to draw a curve that starts at point (r, 0) and then continues up to the left up to an angle of 45 °. ${\displaystyle x^{2}+y^{2}=r^{2}}$

The "fast" direction here is the direction. You always take a step in the positive direction, and every now and then you have to take a step in the "slow", negative direction. ${\displaystyle y}$ ${\displaystyle y}$ ${\displaystyle x}$

The constant square calculations (see circular equation ) or possibly even trigonometric or root calculations are avoided again by resolving them into individual steps and recursively calculating the terms from the preceding ones.

Mathematically: From the circular equation one arrives at the transformed equation

${\displaystyle 0=x^{2}+y^{2}-r^{2}}$,

whereby it does not have to be calculated explicitly, ${\displaystyle r^{2}}$

${\displaystyle x^{2}=(x_{\mathrm {vorher} }-1)^{2}=x_{\mathrm {vorher} }^{2}-2\cdot x_{\mathrm {vorher} }+1}$(corresponding to ), ${\displaystyle y}$

Here, too, it does not have to be included as a separate variable, but only the difference from one step to the next is added to the error element. Again, the zero in the equation is replaced by the error term. ${\displaystyle x_{\mathrm {vorher} }^{2}}$ ${\displaystyle (-2\cdot x_{\mathrm {vorher} }+1)}$

In addition, you have to add the center point coordinates when setting the pixels. However, these constant fixed point additions do not noticeably limit the performance , since you save yourself squaring or even drawing roots in the innermost loop.

The approach based on the circular equation ensures that the coordinates deviate from the ideal curve by a maximum of 1 pixel, the digitization error. The initialization of the error element should now cause the first step in the slow direction to take place when the real circular curve has come inward by half a pixel in the slow coordinate. Details on the calculation below; it amounts to an initialization of the error term with the radius r.

The formulation is shown here again only for the first octant, and again the other octants result from a change of sign in and and role reversal of and . The extension to the full circle, as it is suitable for graphic displays but not for plotters, is included in comments. ${\displaystyle dx}$ ${\displaystyle dy}$ ${\displaystyle x}$ ${\displaystyle y}$

 REM Bresenham-Algorithmus für einen Achtelkreis in Pseudo-Basic
 REM gegeben seien r, xmittel, ymittel
 REM Initialisierungen für den ersten Oktanten
 x = r
 y = 0
 fehler = r
 REM "schnelle" Richtung ist hier y!
 SETPIXEL xmittel + x, ymittel + y

 REM Pixelschleife: immer ein Schritt in schnelle Richtung, hin und wieder auch einer in langsame
 WHILE y < x
    REM Schritt in schnelle Richtung
    dy = y*2+1 : REM bei Assembler-Implementierung *2 per Shift
    y = y+1
    fehler = fehler-dy
    IF fehler<0 THEN
       REM Schritt in langsame Richtung (hier negative x-Richtung)
       dx = 1-x*2 : REM bei Assembler-Implementierung *2 per Shift
       x = x-1
       fehler = fehler-dx
    END IF
    SETPIXEL  xmittel+x, ymittel+y
    REM Wenn es um einen Bildschirm und nicht mechanisches Plotten geht,
    REM kann man die anderen Oktanten hier gleich mit abdecken:
    REM SETPIXEL xmittel-x, ymittel+y
    REM SETPIXEL xmittel-x, ymittel-y
    REM SETPIXEL xmittel+x, ymittel-y
    REM SETPIXEL xmittel+y, ymittel+x
    REM SETPIXEL xmittel-y, ymittel+x
    REM SETPIXEL xmittel-y, ymittel-x
    REM SETPIXEL xmittel+y, ymittel-x
 WEND

A possible implementation of the Bresenham algorithm for a full circle in C. Here another variable is included for the quadratic terms, which corresponds to the term above, it only has to be increased by 2 from one step to the next: ${\displaystyle 2\cdot n+1}$

  void rasterCircle(int x0, int y0, int radius)
  {
    int f = 1 - radius;
    int ddF_x = 0;
    int ddF_y = -2 * radius;
    int x = 0;
    int y = radius;

    setPixel(x0, y0 + radius);
    setPixel(x0, y0 - radius);
    setPixel(x0 + radius, y0);
    setPixel(x0 - radius, y0);

    while(x < y)
    {
      if(f >= 0)
      {
        y--;
        ddF_y += 2;
        f += ddF_y;
      }
      x++;
      ddF_x += 2;
      f += ddF_x + 1;

      setPixel(x0 + x, y0 + y);
      setPixel(x0 - x, y0 + y);
      setPixel(x0 + x, y0 - y);
      setPixel(x0 - x, y0 - y);
      setPixel(x0 + y, y0 + x);
      setPixel(x0 - y, y0 + x);
      setPixel(x0 + y, y0 - x);
      setPixel(x0 - y, y0 - x);
    }
  }

Derivation of the error element initialization

The point of intersection at which the circular line has come inward by 1/2 pixel is calculated using the circular equation:

${\displaystyle \,x^{2}+y^{2}=r^{2}}$    or    ${\displaystyle y={\sqrt {r^{2}-x^{2}}}}$

At the point in question (x ₁ , y ₁ ) the following should apply:, so it results: ${\displaystyle \,x_{1}=r-1/2}$

${\displaystyle y_{1}={\sqrt {r^{2}-(r-1/2)^{2}}}={\sqrt {r^{2}-(r^{2}-r+1/4)}}={\sqrt {r-1/4}}}$

Since no x-step should have taken place up to this point, the error element is included

${\displaystyle \sum _{y=0}^{y_{1}}(2*y+1)=y_{1}^{2}}$

to initialize, where y ₁ ² becomes r by rounding.

Example: in the picture above: r = 11, y ₁ = 3 (rounded off), error term for y = y ₁ = 3 is 1 + 3 + 5 = 9, error term for y = 4 is 1 + 3 + 5 + 7 = 16 . If the error element was initialized with r = 11, the first change in sign and thus the first x step actually takes place at the transition from y ₁ to y ₁ +1.

Draw incomplete octants

The above implementations only ever draw complete octants or circles. If you only want to draw a certain arc from an angle to an angle , you have to implement it in such a way that you calculate the and coordinates of these endpoints in advance, in which case you inevitably have to resort to trigonometry or calculus of roots (see also Heron method ). Then you let the Bresenham algorithm run over the entire octant or circle and only set the pixels if they fall within the desired range. The algorithm can be terminated prematurely after this section of the curve has been completed. ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle x}$ ${\displaystyle y}$

Ellipses

There are also several possible approaches for ellipses . In the case of paraxial ellipses, one can use the corresponding equation

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$

where and indicate the two semiaxis lengths, go out and then proceed similarly to the circle above. ${\displaystyle a}$ ${\displaystyle b}$

But one can also generate such axially parallel ellipses by scaling the drawn and values ​​(and possibly horizontal or vertical line extensions) on the basis of the circular algorithm. The circle algorithm is used with the smaller elliptical axis as the radius and a value is added in the other direction, which in turn can be determined using the Bresenham line algorithm increasing from the pole to the equator. Since the ellipse has to be stretched in the longer axis direction, you not only set individual pixels, but also have to draw a line (though a simple, horizontal or vertical one) from the previous point to the next. ${\displaystyle x}$ ${\displaystyle y}$

A general ellipse can be obtained from such an axis parallel by subjecting the entire graphic to a shear . An additional Bresenham line algorithm is used again to determine the offset in one of the axis directions increasing and to include it in every coordinate to be drawn.

Compact variant

As with the algorithm for the line, the circle variant can also be formulated xy-symmetrically. This means that a continuous quarter circle can be drawn, which is useful for ellipses.

void ellipse(int xm, int ym, int a, int b)
{
   int dx = 0, dy = b; /* im I. Quadranten von links oben nach rechts unten */
   long a2 = a*a, b2 = b*b;
   long err = b2-(2*b-1)*a2, e2; /* Fehler im 1. Schritt */

   do {
       setPixel(xm+dx, ym+dy); /* I. Quadrant */
       setPixel(xm-dx, ym+dy); /* II. Quadrant */
       setPixel(xm-dx, ym-dy); /* III. Quadrant */
       setPixel(xm+dx, ym-dy); /* IV. Quadrant */

       e2 = 2*err;
       if (e2 <  (2*dx+1)*b2) { dx++; err += (2*dx+1)*b2; }
       if (e2 > -(2*dy-1)*a2) { dy--; err -= (2*dy-1)*a2; }
   } while (dy >= 0);

   while (dx++ < a) { /* fehlerhafter Abbruch bei flachen Ellipsen (b=1) */
       setPixel(xm+dx, ym); /* -> Spitze der Ellipse vollenden */
       setPixel(xm-dx, ym);
   }
}

The algorithm always tests a diagonal step and corrects it if the deviation is too great. However, the steps always end in the next quadrant and then the process is terminated too early for flat ellipses (b = 1). In these cases, a supplement is necessary. The error variable must have 3 times the value range (number of digits, bits) of the radius (semi-axes) (about 64-bit or floating point number).

The method can also be used for circles (a = b = r). The simplification (by shortening the error variable by 2r ^2, for example ) then leads to the circle examples shown above. Four seamless quarter circles become a continuous full circle, as is necessary with plotters.

Further generalizations

As early as 1968, the idea of ​​generalizing the Bresenham algorithm for the digitization of curves described by cubic equations was published. The details were not really carried out until 1993 and later. a. from Pitteway and independently thereof in US Pat . No. 5,717,847 . The method was used in the lithography tool LION-LV1 for structuring in the sub-micrometer range of geometric figures bordered by rational cubic Bézier curves .

Web links

Commons : Bresenham Algorithm  - collection of images, videos and audio files

• Bresenham's algorithm (NIST Dictionary of Algorithms and Data Structures) - Background to the Bresenham algorithm, with original source code
• Rasterization of lines, circles, ellipses (Uni Magdeburg, Institute for Simulation and Graphics) - Java applet for reproducing the Bresenham algorithm
• The Beauty of Bresenham's Algorithm - A Simple Implementation for Drawing Lines, Circles, Ellipses, and Bézier Curves
  • Online JavaScript demo

Individual evidence

1. ^ JE Bresenham: Algorithm for computer control of a digital plotter. In: IBM Systems Journal , 4, 1, 1965, pp. 25–30, ISSN  0018-8670 , cse.iitb.ac.in (PDF; 223 kB; English) Already presented in 1963 as a lecture at the ACM National Conference in Denver .
   The first publication of the basic idea for generating circles can be found in: HB Keller, JR Swenson: Experiments on the lattice problem of Gauss . (PDF; 222 kB) In: Math. Comp. , 17, 1963, pp. 223-230, Section 3.
2. ↑ MLV Pitteway: Algorithm for Drawing Ellipses or Hyperbolae with a digital plotter . In: Computer J. , 10 (3) November 1967, pp. 282–289 (English)
3. ↑ JRVan Aken: An Efficient Ellipse Drawing Algorithm . In: CG&A , 4 (9), September 1984, pp. 24-35 (English)
4. ^ FG Stockton: XY Move Plotting . In: Communications of the ACM , vol. 4, no. 6, April 1963, p. 161 (English)
5. ↑ RJ Botting, MLV Pitteway: Cubic extension of a conic section algorithm. In: Computer Journal , 11, 1968, p. 120
6. ↑ Fiaz Hussain, Michael LV Pitteway: rasterizing the outlines of fonts. (PDF; 162 kB) In: Electronic Publishing , Volume 6, 1993, No. 3, pp. 171-181
7. ↑ Method for generating plane technical curves or contours , filed Dec. 23, 1993
8. ↑ R. Plontke: LION-LV1: A lithography system for integrated optics and nanostructures. In: Jena Yearbook on Technology and Industrial History , Volume 9, 2006, pp. 535–566