Euler gyro

Fig. 1: Realization of an Euler gyro

In the gyro theory, the force-free top is a top on which no external forces act. The equations of motion was first Leonhard Euler solved in 1758, in whose honor the gyro also Euler roundabout is called.

The determining equations are the Euler-Poisson equations , the solutions of which can only be derived here, with the Lagrange gyro and the Kowalewskaja gyro, with any initial conditions, and with algebraic integrals.

The angular velocities can be expressed with Jacobi's elliptical functions , which in the case of a symmetrical top change into the sine and cosine . Here the top shows particularly regular and clear behavior, see #Description of the movement . The Poinsotsche construction guides the movement of the rolling of the Energieellipsoids back on a plane.

Except in the weightlessness a centrifugal force-free can be realized in a gravitational field, by rotation in its center of gravity, for example as in Fig. 1 gimbals is suspended. The Euler gyro finds z. B. Technical application in gyroscopic compasses and gyroscopic control systems.

Designations

→ Main article : gyro  and gyro theory

The movements of the force-free top are called nutation in top technology . The azimuthal rotation is also called precession. Further designations are given in the main articles.

General characteristics of the movement of force-free tops

Gyroscopic equations

→ Main article : Euler gyro equations  and Euler-Poisson equations

The gyro's motion function is determined by the gyroscopic equations established by Leonhard Euler, which, if the center of mass is at the base, have the same content as the Euler-Poisson equations for the heavy gyro . The equations refer to the principal axis system rotating with the body and form the autonomous ordinary differential equation system

${\displaystyle {\begin{aligned}\Theta _{1}{\dot {\omega }}_{1}=&(\Theta _{2}-\Theta _{3})\omega _{2}\omega _{3}\\\Theta _{2}{\dot {\omega }}_{2}=&(\Theta _{3}-\Theta _{1})\omega _{3}\omega _{1}\\\Theta _{3}{\dot {\omega }}_{3}=&(\Theta _{1}-\Theta _{2})\omega _{1}\omega _{2}\\{\dot {L}}_{1}=&\left({\frac {1}{\Theta _{3}}}-{\frac {1}{\Theta _{2}}}\right)L_{2}L_{3}\\{\dot {L}}_{2}=&\left({\frac {1}{\Theta _{1}}}-{\frac {1}{\Theta _{3}}}\right)L_{3}L_{1}\\{\dot {L}}_{3}=&\left({\frac {1}{\Theta _{2}}}-{\frac {1}{\Theta _{1}}}\right)L_{1}L_{2}\end{aligned}}}$

In each case, k = 1,2,3

Θ _{k are} the main moments of inertia ,

L _k = Θ _k ω _k the angular momentum and

ω _{k are} the angular velocities

in the main axis system. The over point forms the time derivative .

The gyroscopic effect of the Euler forces is on the left and that of the centrifugal forces on the right , see the law of swirl on the rigid body . The Euler forces are an expression of the angular accelerations that are caused here by the centrifugal forces in the top. Conversely, the angular accelerations lead to a change in the axis and speed of rotation, which affects the centrifugal forces. The result of this dynamic interplay is the nutation of the force-free top.

Integrals of motion

The rotary motion of a force-free top is subject to two conditions in addition to the top equations.

On the one hand, the conservation of angular momentum in the spatially fixed xyz system forces that all three angular momentum components of

${\displaystyle {\vec {L}}=L_{x}{\hat {e}}_{x}+L_{y}{\hat {e}}_{y}+L_{z}{\hat {e}}_{z}={\text{const.}}}$

are constant in the force-free case. As a second condition, the rotational energy E _{rot is} retained according to the law of conservation of energy .

In the local main axis system fixed to the body, this means:

${\displaystyle {\begin{aligned}L^{2}:=&L_{1}^{2}+L_{2}^{2}+L_{3}^{2}=&\Theta _{1}^{2}\omega _{1}^{2}+\Theta _{2}^{2}\omega _{2}^{2}+\Theta _{3}^{2}\omega _{3}^{2}=&{\text{const.}}\\2E_{\mathrm {rot} }=&{\frac {L_{1}^{2}}{\Theta _{1}}}+{\frac {L_{2}^{2}}{\Theta _{2}}}+{\frac {L_{3}^{2}}{\Theta _{3}}}=&\Theta _{1}\omega _{1}^{2}+\Theta _{2}\omega _{2}^{2}+\Theta _{3}\omega _{3}^{2}=&{\text{const.}}\end{aligned}}}$

The conservation of L _{x, y, z} , L ² and E _rot is in accordance with the above gyro equations, which can be proven by time derivative of the constants and inserting the gyro equations and the Euler angles of the gyro theory . The constants of motion are called integrals in gyro theory .

The above equations define ellipsoids . The parts of the equation expressed with the angular velocities represent the twist ellipsoid in the upper equation and the energy ellipsoid in the lower one. The surfaces expressed with the angular momentum are the twist sphere in the upper equation and the MacCullagh ellipsoid in the lower equation . The angular velocities and angular momentum are part of both surfaces.

The swirl sphere and the MacCullagh ellipsoid only have points in common if the limits for angular momentum and rotational energy are adhered to. Multiplication of 2 E _red with - L ² and L ² with 2 E _red and addition gives:

${\displaystyle (2E_{\mathrm {rot} }\Theta _{1}-L^{2})\Theta _{1}\omega _{1}^{2}+(2E_{\mathrm {rot} }\Theta _{2}-L^{2})\Theta _{2}\omega _{2}^{2}+(2E_{\mathrm {rot} }\Theta _{3}-L^{2})\Theta _{3}\omega _{3}^{2}=0}$

The equation for the polar cone , which consists of the points for which is, results from: ${\displaystyle X/\omega _{1}=Y/\omega _{2}=Z/\omega _{3}}$

${\displaystyle (2E_{\mathrm {rot} }\Theta _{1}-L^{2})\Theta _{1}X^{2}+(2E_{\mathrm {rot} }\Theta _{2}-L^{2})\Theta _{2}Y^{2}+(2E_{\mathrm {rot} }\Theta _{3}-L^{2})\Theta _{3}Z^{2}=0}$

With the asymmetrical Euler gyro this represents an elliptical cone and with the symmetrical one a circular cone , see #Description of the movement .

MacCullagh's interpretation of the gyroscopic motion

Fig. 3: MacCullagh ellipsoid (yellow), swirl sphere (green), swirl pole curves (red) and tangential plane (gray) meet in angular momentum . The current angular velocity is perpendicular to the tangential plane. ${\displaystyle {\vec {L}}}$ ${\displaystyle {\vec {\omega }}}$

By James MacCullagh a geometric interpretation of precession, like the dates Poinsot'sche construction but clearly not as fertile as the latter. The angular momentum is constant in the space-fixed system, forms the invariable straight line through the support point and touches the MacCullagh ellipsoid at any time , which in the body-fixed system consists of the end points of all angular momentum that lead to the current rotational energy, see Fig. 3. The MacCullagh ellipsoid moves with the top in such a way that the angular momentum is simultaneously on the ellipsoid and the swirl sphere, whereby the swirl pole curves drawn in red arise. The points on the swirl pole curves therefore all have the same distance from the support point. The perpendicular of the support point on the tangential plane to the MacCullagh ellipsoid at the end point of the angular momentum is parallel to the current angular velocity. Said tangential plane is, unlike the invariable plane of Poinsot's construction, not fixed in space.

The cross product of angular velocity and angular momentum is inversely equal to the gyroscopic effect of the centrifugal forces, which is exactly the opposite of the gyroscopic effect of the Euler forces , which are the expression of changes in the rotational speed and axis, i.e. the orientation of the MacCullagh ellipsoid, see also #Gyroscopic equations . ${\displaystyle ({\vec {\omega }}\times {\vec {L}})}$

Stability considerations

Fig. 4: Carrier curves of the solutions of the gyroscopic equations on the swirl sphere.

In Fig. 4, the swirl sphere and swirl pole curves belonging to different rotational energies are drawn viewed from three directions. The swirl pole curves are closed curves (red and blue in the picture), which can be circular , elliptical or taco shaped and, like the MacCullagh ellipsoid, are symmetrical to the planes spanned by the main axes . Pericycloidal movements take place on the blue curves while the movement is called epicycloidal on the red curves, see Poinsot's construction . In between is the separatrix , which separates these two forms of movement from each other.

If the angular momentum is in the vicinity of the main axis of inertia with the largest or smallest moment of inertia (blue or red points in Fig. 4), then it also remains in its vicinity, because these points are surrounded by the swirl pole curves. Therefore these axes of rotation are stable axes of rotation of free rotation. Their points of intersection with the swirl sphere are elliptical fixed points of an autonomous differential equation .

A measure for the stability of the axes of rotation can be derived from the axis ratios of the ellipses, see stability considerations in Poinsot's construction.

If the angular momentum lies exactly on the 2-axis (black point), then it remains there, otherwise it moves away from the intersection, because this is not orbited by the twist pole curves. The 2-axis is an unstable axis of rotation, it meets the MacCullagh ellipsoid in a hyperbolic fixed point or saddle point of the associated autonomous differential equation (see also # Stability of the movement of asymmetrical tops below). The movement on the separatrix is ​​unstable, because with the slightest disturbance the path becomes epi- or pericycloid.

If the main moments of inertia Θ _1.2 coincide, which means that the top becomes a symmetrical top , then the MacCullagh ellipsoid is an ellipsoid of revolution around the 3-axis, the separatrix becomes a great circle in the 1-2 plane and the swirl pole curves are parallel small circles to this. The rotation around the figure axis (axis of symmetry 3) is in any case stable, because the twist pole curves surround this axis as small circles. The equatorial main axes that are perpendicular to the figure axis show complex stability behavior:

• With regard to the angular velocities and the angle of inclination ϑ , rotations around an equatorial axis are stable, ${\displaystyle \omega _{3},\,{\dot {\psi }},\,{\dot {\varphi }}}$
• With regard to the angles ψ and φ and the angular velocities ω _1,2 , rotations around an equatorial axis are unstable.

Because if the rotation around the 1-axis is disturbed by a small angular speed around the 3-axis, the twist pole curve becomes a small circle around the 3-axis and the axis of rotation revolves around the figure axis parallel to the 1-2 plane. So it does not stay close to the 1-axis, which means instability of ω ₁ with respect to disturbance of ω ₃ . However, a small disturbance of the axial angular velocity ω ₃ or the angle of inclination ϑ leads to a change that remains small. In the same way, the other quantities are examined for stability against disturbances.

For the stability of the spherical top , see there.

The movements of the angular momentum in the local frame of reference

The angular momentum wanders through the twist pole curves drawn in Fig. 3 and Fig. 4 without ever standing still or even changing the direction of rotation. Because apart from the main axes of inertia, at most one component of the angular momentum disappears and therefore, according to the gyroscopic equations, the local velocities can not all be zero at once. ${\displaystyle {\dot {L}}_{1,2,3}}$

In the absence of external influences, the power-free top does not make any jumps. The local components of the angular momentum are thus Lipschitz continuous and therefore the trajectories of the angular momentum cannot intersect according to Picard-Lindelöf's theorem . This condition is violated on the separatrix ( dashed black in Fig. 4 ). An aperiodic movement therefore develops on it, because the angular momentum cannot exceed the intersection points on the 2-axis. The main axis of inertia with the mean main moment of inertia approaches the axis given by the angular momentum asymptotically on a loxodrome , see #Movement on the separatrix below.

If the rotational energy decreases, for example through dissipation , the axis of rotation will move in the direction of the axis with the greatest moment of inertia, which is the 3-axis in Fig. 4 , because there the MacCullagh ellipsoid with the smallest energy touches the swirl sphere.

Force-free symmetrical top

With a symmetrical top, two of the three main moments of inertia are by definition the same. The movement is a regular and descriptive regular precession . Without loss of generality, Θ ₁ = Θ ₂ =: Θ ₀ and rotation around the 3-axis - the figure axis - is assumed.

Description of the movement

In the case of a symmetrical top, the third gyro equation is simplified to in the force-free case , so that the angular velocity ω ₃ and thus also the angular momentum L _{3 are} constant. The other two gyroscopic equations form the linear ordinary differential equation system ${\displaystyle \Theta _{3}\,{\dot {\omega }}_{3}=0}$

${\displaystyle {\begin{aligned}0=&{\dot {\omega }}_{1}+\Omega \omega _{2}\\0=&{\dot {\omega }}_{2}-\Omega \omega _{1}\end{aligned}}}$

with constant coefficient . The time derivative of the equations leads to two decoupled differential equations , the general solution of which can be represented as follows: ${\displaystyle \Omega :={\tfrac {\Theta _{3}-\Theta _{0}}{\Theta _{0}}}\omega _{3}}$ ${\displaystyle {\ddot {\omega }}_{1,2}+\Omega ^{2}\omega _{1,2}=0}$

${\displaystyle {\begin{pmatrix}\omega _{1}(t)\\\omega _{2}(t)\end{pmatrix}}={\begin{pmatrix}\cos(\Omega \,t)&-\sin(\Omega \,t)\\\sin(\Omega \,t)&\cos(\Omega \,t)\end{pmatrix}}{\begin{pmatrix}\omega _{1}(0)\\\omega _{2}(0)\end{pmatrix}}}$

The values ω _1,2 (0) are initial conditions at time t  = 0 and are mapped to the current values by a 2 × 2 rotation matrix . If ω ₃ (0) = 0 and / or ω ₁ (0) =  ω ₂ (0) = 0, ω ₁ and ω ₂ remain constant and the gyroscope rotates constantly or, in the special case, remains ω _{1,2 , 3} (0) = 0 at rest.

Fig. 5: Components of motion in a force-free top ( β = ϑ )

To sketch the general movement,  a Cartesian coordinate system with x, y and z axes is placed in the center of mass of the top at time t = 0 so that the figure axis and the angular velocity lie in the xz plane, see Fig. 5. The main axis system is initially aligned so that the angular velocity and the figure axis lie in the 13-plane and enclose an angle λ (shown differently in Fig. 5). Then ω ₁ (0) =  ω  sin (λ), ω ₂ (0) = 0 and ω ₃ (0) =  ω  cos (λ) with the magnitude of the angular velocity. As with the Euler angles in gyro theory , the main axes are designated with ê _1,2,3 . ${\displaystyle \omega :=|{\vec {\omega }}|}$

The solution of the gyroscopic equations given above results with the given initial conditions:

${\displaystyle {\begin{pmatrix}\omega _{1}(t)\\\omega _{2}(t)\end{pmatrix}}={\begin{pmatrix}\cos(\Omega \,t)&-\sin(\Omega \,t)\\\sin(\Omega \,t)&\cos(\Omega \,t)\end{pmatrix}}{\begin{pmatrix}\omega \sin(\lambda )\\0\end{pmatrix}}={\begin{pmatrix}\omega \sin(\lambda )\cos(\Omega \,t)\\\omega \sin(\lambda )\sin(\Omega \,t)\end{pmatrix}}}$

The difference vector has the constant amount and rotates around the figure axis with the speed . The figure axis and the angular velocity therefore always enclose the same angle, namely λ. In the main axis system fixed to the body, the angular velocity executes a rotary movement around the figure axis and forms the pole cone fixed to the body with half the opening angle λ (red in Fig. 5 and Fig. 6 ). ${\displaystyle {\vec {\omega }}_{\bot }:={\vec {\omega }}-\omega _{3}{\hat {e}}_{3}=\omega _{1}{\hat {e}}_{1}+\omega _{2}{\hat {e}}_{2}}$ ${\displaystyle \omega _{\bot }:={\sqrt {\omega _{1}^{2}+\omega _{2}^{2}}}=\omega \left|\sin(\lambda )\right|}$ ${\displaystyle {\tfrac {\Omega }{2\pi }}}$

The angular momentum is in the spatially fixed system

${\displaystyle {\begin{aligned}{\vec {L}}=&\Theta _{0}\omega _{1}{\hat {e}}_{1}+\Theta _{0}\omega _{2}{\hat {e}}_{2}+\Theta _{3}\omega _{3}{\hat {e}}_{3}=\Theta _{0}({\vec {\omega }}-\omega _{3}{\hat {e}}_{3})+\Theta _{3}\omega _{3}{\hat {e}}_{3}\\=&\Theta _{0}{\vec {\omega }}+(\Theta _{3}-\Theta _{0})\omega _{3}{\hat {e}}_{3}\end{aligned}}}$

constant around the center of mass (green in Fig. 5 ) and forms the precession axis . The latter decomposition shows that the angular momentum lies in the plane spanned by the figure axis and the angular velocity , the precession plane . The figure axis and the angular velocity rotate together around the spatially fixed precession axis. ${\displaystyle {\vec {\omega }}}$

The coordinate system can now - as in Fig. 5 - be aligned so that the angular momentum points in the z-direction and is therefore valid. Because the rotational energy ${\displaystyle {\vec {L}}=:L{\hat {e}}_{z}}$

${\displaystyle E_{\rm {rot}}={\frac {1}{2}}{\vec {\omega }}\cdot {\vec {L}}={\frac {1}{2}}{\vec {\omega }}\cdot L{\hat {e}}_{z}=:{\frac {1}{2}}\omega _{z}L}$

also does not change, the z-component ω _{z of} the angular velocity in the direction of the angular momentum is constant. The angular velocity thus also moves around the spatially fixed z-direction on a cone, the spatially fixed track cone (blue in Fig. 5 and Fig. 6 , there called “ spatially fixed gear pole cone ”).

Fig. 6: Form of movement of an oblate, force-free top

The gear pole cone rolls on the locking pole cone. In the case of the prolate (stretched) top, Θ ₀  > Θ ₃ and the gear pole cone rolls off the outside of the locking pole cone, as in Fig. 5 . In the oblate (flattened) top, Θ ₃  > Θ ₀ and the gear pole cone rolls on the inside of the locking pole cone as in Fig. 6 .

Rolling is easy , because the common surface line of the detent pole and gear pole cone is the momentary axis of rotation set by the angular velocity, which goes through the center of mass at rest (shown differently in Fig. 6). The particles of the gyro on the axis of rotation stand still as long as they do, the detent pole cone is at rest anyway, and slip between the gear and detent pole cone is therefore excluded.

The angle ϑ between the figure axis and the angular momentum as well as the z component ω _{z of} the angular velocity can be determined with the mechanical analysis in the following section.

Movement function of the symmetrical top

If, as in the previous section, the angular momentum points in the direction of the z-axis and the angular velocity ω and the angle λ are specified (all these quantities are constants of the movement), then the angular momentum is calculated

${\displaystyle L={\sqrt {\Theta _{3}^{2}\cos ^{2}(\lambda )+\Theta _{0}^{2}\sin ^{2}(\lambda )}}\,\omega \,,}$

the angular velocities

${\displaystyle {\begin{aligned}\Omega =&{\frac {\Theta _{3}-\Theta _{0}}{\Theta _{0}}}\omega \cos(\lambda )\\\omega _{1}=&{\dot {\psi }}\sin(\vartheta )\sin(\varphi )=\omega \sin(\lambda )\cos(\Omega t)\\\omega _{2}=&{\dot {\psi }}\sin(\vartheta )\cos(\varphi )=\omega \sin(\lambda )\sin(\Omega t)\\\omega _{3}=&{\dot {\psi }}\cos(\vartheta )+{\dot {\varphi }}=\omega \cos(\lambda )\end{aligned}}}$

and the angles

${\displaystyle \psi ={\frac {\pi }{2}}+{\frac {L}{\Theta _{0}}}\,t\,,\quad \vartheta =\arctan \left({\frac {\Theta _{0}}{\Theta _{3}}}\tan(\lambda )\right)\,,\quad \varphi ={\frac {\pi }{2}}-\Omega t}$

in radians . The function tan is the tangent and arctan is its arc function . The precession plane spanned by the figure axis and the angular velocity, in which the angular momentum also lies, closes the angle with the xz plane

${\displaystyle \mu ={\frac {\Theta _{3}\cos ^{2}(\lambda )+\Theta _{0}\sin ^{2}(\lambda )}{\sqrt {\Theta _{3}^{2}\cos ^{2}(\lambda )+\Theta _{0}^{2}\sin ^{2}(\lambda )}}}\,\omega t}$

a.

proof
The angular momentum is constant in the absence of external moments and wise in a space-fixed Cartesian xyz coordinate system in the z direction. Then with the Euler angles in the gyro theory we get : ${\displaystyle {\begin{aligned}{\vec {L}}=&L{\hat {e}}_{z}=\Theta _{0}\omega _{1}{\hat {e}}_{1}+\Theta _{0}\omega _{2}{\hat {e}}_{2}+\Theta _{3}\omega _{3}{\hat {e}}_{3}\\L=&{\vec {L}}\cdot {\hat {e}}_{z}=\Theta _{0}\omega _{1}\sin(\vartheta )\sin(\varphi )+\Theta _{0}\omega _{2}\sin(\vartheta )\cos(\varphi )+\Theta _{3}\omega _{3}\cos(\vartheta )\\=&\Theta _{0}{\dot {\psi }}\sin ^{2}(\vartheta )+\Theta _{3}\omega _{3}\cos(\vartheta )\end{aligned}}}$ According to the gyroscopic equations, the angular velocity ω 3 is just like the angular momentum L and ${\displaystyle L_{3}=\Theta _{3}\omega _{3}=L\cos(\vartheta )}$ constant, which is why the angle ϑ is also constant. It follows ${\displaystyle L={\frac {\Theta _{3}\omega _{3}}{\cos(\vartheta )}}\quad {\text{und}}\quad {\dot {\psi }}={\frac {\Theta _{3}\omega _{3}}{\Theta _{0}\cos(\vartheta )}}={\frac {L}{\Theta _{0}}}}$ With the gyroscopic equations and the relationships between the angular velocities and the angles it becomes apparent ${\displaystyle {\begin{aligned}{\ddot {\vartheta }}=&{\dot {\omega }}_{1}\cos(\varphi )-\omega _{1}\sin(\varphi ){\dot {\varphi }}-{\dot {\omega }}_{2}\sin(\varphi )-\omega _{2}\cos(\varphi ){\dot {\varphi }}\\=&-{\dot {\psi }}\sin(\vartheta )\left({\frac {\Theta _{0}-\Theta _{3}}{\Theta _{0}}}\omega _{3}-{\dot {\varphi }}\right)=0\end{aligned}}}$ If there is no rotation (because of L  = 0) and if sin ( ϑ ) = 0 the top rotates uniformly around its figure axis. Otherwise it results ${\displaystyle {\dot {\psi }}=0}$ ${\displaystyle {\dot {\varphi }}={\frac {\Theta _{0}-\Theta _{3}}{\Theta _{0}}}\omega _{3}=-\Omega }$ The z component ω z of the angular velocity is ${\displaystyle \omega _{z}=(\omega _{1}{\hat {e}}_{1}+\omega _{2}{\hat {e}}_{2}+\omega _{3}{\hat {e}}_{3})\cdot {\hat {e}}_{z}={\frac {\Theta _{3}\sin ^{2}(\vartheta )+\Theta _{0}\cos ^{2}(\vartheta )}{\Theta _{0}\cos(\vartheta )}}\omega _{3}}$
Initial conditions
At time t  = 0 and ω 3 retains this value . The angle ϑ can now be expressed as a function of the angle λ: ${\displaystyle \omega _{3}={\vec {\omega }}\cdot {\hat {e}}_{3}=\omega \cos(\lambda )}$ ${\displaystyle {\begin{aligned}\omega \cos(\lambda )=&\omega _{3}={\dot {\psi }}\cos(\vartheta )+{\dot {\varphi }}={\dot {\psi }}\cos(\vartheta )-\Omega \\\omega \sin(\lambda )=&\omega _{\bot }={\sqrt {\omega _{1}^{2}+\omega _{2}^{2}}}={\dot {\psi }}\sin(\vartheta )\\\rightarrow \cot(\lambda )=&\cot(\vartheta )-{\frac {\Omega }{{\dot {\psi }}\sin(\vartheta )}}=\cot(\vartheta )+{\frac {\Theta _{0}-\Theta _{3}}{\Theta _{0}}}\omega _{3}{\frac {\Theta _{0}\cos(\vartheta )}{\Theta _{3}\omega _{3}\sin(\vartheta )}}\\=&\cot(\vartheta )+{\frac {\Theta _{0}-\Theta _{3}}{\Theta _{3}}}\cot(\vartheta )\\\rightarrow \tan(\vartheta )=&{\frac {\Theta _{0}}{\Theta _{3}}}\tan(\lambda )\,.\end{aligned}}}$ The cotangent cot is the reciprocal of the tangent. Because of and it follows for the angular momentum: ${\displaystyle \cos x=(1+\tan ^{2}x)^{-1/2}}$ ${\displaystyle \tan(\vartheta )={\tfrac {\Theta _{0}}{\Theta _{3}}}\tan(\lambda )}$ ${\displaystyle L={\frac {\Theta _{3}\omega _{3}}{\cos(\vartheta )}}={\frac {\Theta _{3}\omega \cos(\lambda )}{\cos(\vartheta )}}={\sqrt {\Theta _{3}^{2}\cos ^{2}(\lambda )+\Theta _{0}^{2}\sin ^{2}(\lambda )}}\,\omega \,.}$ The specifications ${\displaystyle {\begin{aligned}\omega _{1}(t=0)=&{\dot {\psi }}\sin(\vartheta )\sin(\varphi )=\omega \sin(\lambda )\sin(\varphi )\,{\stackrel {\displaystyle !}{=}}\,\omega \sin(\lambda )\\\omega _{2}(t=0)=&{\dot {\psi }}\sin(\vartheta )\cos(\varphi )=\omega \sin(\lambda )\cos(\varphi )\,{\stackrel {\displaystyle !}{=}}\,0\end{aligned}}}$ can be satisfied with the initial value for the angle φ such that . The angular velocity with the addition theorems at time t  = 0 reads : ${\displaystyle {\tfrac {\pi }{2}}}$ ${\displaystyle \varphi ={\tfrac {\pi }{2}}-\Omega t}$ ${\displaystyle {\vec {\omega }}=\omega \sin(\lambda ){\hat {e}}_{1}+\omega \cos(\lambda ){\hat {e}}_{3}=\omega {\begin{pmatrix}\sin(\psi )\sin(\vartheta -\lambda )\\-\cos(\psi )\sin(\vartheta -\lambda )\\\cos(\vartheta -\lambda )\end{pmatrix}}\,.}$ So that this lies in the xz plane, the initial value of ψ is set to, so that ${\displaystyle {\tfrac {\pi }{2}}}$ ${\displaystyle \psi ={\frac {\pi }{2}}+{\dot {\psi }}t={\frac {\pi }{2}}+{\frac {L}{\Theta _{0}}}t}$ results. If the angle of rotation of the precession plane around the z-axis is denoted by µ and has the value zero at the beginning, then with the above ω z and tan ( ϑ ), as well as ω 3 = ω cos (λ): ${\displaystyle \cos(\vartheta )=(1+\tan ^{2}(\vartheta ))^{-1/2}}$ ${\displaystyle \mu :=\omega _{z}t={\frac {\Theta _{3}\cos ^{2}(\lambda )+\Theta _{0}\sin ^{2}(\lambda )}{\sqrt {\Theta _{3}^{2}\cos ^{2}(\lambda )+\Theta _{0}^{2}\sin ^{2}(\lambda )}}}\,\omega t\,.}$

Force-free asymmetrical top

By definition, asymmetrical gyroscopes have three different main moments of inertia . If such a top rotates around the 3-axis, this movement can be unstable or stable. In the first case, small perturbations increase exponentially and the top begins to tumble, which is explained in the next section. In the stable case, periodic forms of motion develop in the second section. At the end, information is provided about the special case of movement on the Separatrix, which was defined in the section # Stability considerations .

Stability of the movement of asymmetrical tops

Play media file

Fig. 7: Dschanibekow effect: motion of a component around its unstable main axis of inertia filmed in weightlessness. It should be emphasized that the angular momentum of the component is retained.

The main axes with the largest or the smallest main moment of inertia are stable axes of rotation. This has been known since 1851 at the latest and is easy to demonstrate with a rotating table tennis bat. In English, the statement is known as the “sentence about the tennis racket” (tennis racket theorem) . After the Soviet cosmonaut Vladimir Dschanibekow observed the movement of a component around its unstable main axis of inertia during a space flight in 1985, the situation was examined more closely and has been called the " Dschanibekow effect " since then .

To check the stability of the axes of rotation, the gyro should first rotate around the 3-axis: and . The gyro equations are now ${\displaystyle \omega _{3}\neq 0}$ ${\displaystyle |\omega _{1,2}|\ll {\sqrt {|{\dot {\omega }}_{3}|}}}$

${\displaystyle {\begin{aligned}0=&{\dot {\omega }}_{1}-{\frac {\Theta _{2}-\Theta _{3}}{\Theta _{1}}}\omega _{2}\omega _{3}\\0=&{\dot {\omega }}_{2}-{\frac {\Theta _{3}-\Theta _{1}}{\Theta _{2}}}\omega _{3}\omega _{1}\\0=&{\dot {\omega }}_{3}-{\frac {\Theta _{1}-\Theta _{2}}{\Theta _{3}}}\omega _{1}\omega _{2}\approx {\dot {\omega }}_{3}\end{aligned}}}$

As in the section #Description of the motion , derivatives according to time and with the approximate constancy of the angular velocity ω ₃ :

${\displaystyle {\begin{aligned}0=&{\ddot {\omega }}_{1}-{\frac {\Theta _{2}-\Theta _{3}}{\Theta _{1}}}\omega _{3}{\dot {\omega }}_{2}={\ddot {\omega }}_{1}-{\frac {\Theta _{2}-\Theta _{3}}{\Theta _{1}}}{\frac {\Theta _{3}-\Theta _{1}}{\Theta _{2}}}\omega _{3}^{2}\omega _{1}={\ddot {\omega }}_{1}+k\omega _{1}\\0=&{\ddot {\omega }}_{2}-{\frac {\Theta _{3}-\Theta _{1}}{\Theta _{2}}}\omega _{3}{\dot {\omega }}_{1}={\ddot {\omega }}_{2}-{\frac {\Theta _{3}-\Theta _{1}}{\Theta _{2}}}{\frac {\Theta _{2}-\Theta _{3}}{\Theta _{1}}}\omega _{3}^{2}\omega _{2}={\ddot {\omega }}_{2}+k\omega _{2}\\&{\text{mit}}\quad k:={\frac {\Theta _{1}-\Theta _{3}}{\Theta _{2}}}{\frac {\Theta _{2}-\Theta _{3}}{\Theta _{1}}}\omega _{3}^{2}\end{aligned}}}$

If k is negative, there is positive feedback of the angular velocities and thus the rotation around the 3-axis is abandoned and there is a wobble. If k is positive, there are periodic forms of motion around the 3-axis. For this, the main moments of inertia Θ _1.2 must either be both larger or both smaller than the third main moment of inertia Θ ₃ , from which the above statement about the stability of the axes follows.

With very different main moments of inertia, a stable axis of rotation can also appear unstable. Poinsot's construction gives a geometric stability criterion for the main axes of inertia that does justice to this phenomenon.

Motion function of the asymmetrical top

Fig. 8: Time courses of the Jacobi elliptic functions sn, cn and dn at k = 0.95

In the case of an asymmetrical top , the gyro equations can be fulfilled in the force-free case with Jacobi's elliptic functions sn, cn and dn. To do this, the main axes are numbered so that Θ ₁  >  Θ ₂  >  Θ ₃ . From the rotational energy and the square of the amount of the angular momentum

${\displaystyle {\begin{aligned}E_{\text{rot}}:=&{\frac {1}{2}}(\Theta _{1}\omega _{1}^{2}+\Theta _{2}\omega _{2}^{2}+\Theta _{3}\omega _{3}^{2})\\L^{2}:=&{\vec {L}}\cdot {\vec {L}}=\Theta _{1}^{2}\omega _{1}^{2}+\Theta _{2}^{2}\omega _{2}^{2}+\Theta _{3}^{2}\omega _{3}^{2}\end{aligned}}}$

with epicycloidal movements, where L² <2Θ ₂ E is _red , the angular velocities result

${\displaystyle {\begin{aligned}\omega _{1}=&{\sqrt {\frac {L^{2}-2\Theta _{3}E_{\text{rot}}}{\Theta _{1}(\Theta _{1}-\Theta _{3})}}}\operatorname {cn} (z;k),&\omega _{2}=&-{\sqrt {\frac {L^{2}-2\Theta _{3}E_{\text{rot}}}{\Theta _{2}(\Theta _{2}-\Theta _{3})}}}\operatorname {sn} (z;k)\\\omega _{3}=&{\sqrt {\frac {2\Theta _{1}E_{\text{rot}}-L^{2}}{\Theta _{3}(\Theta _{1}-\Theta _{3})}}}\operatorname {dn} (z;k),&z=&a(t-t_{0})\end{aligned}}}$

with the frequency a and the elliptical module k

${\displaystyle a={\sqrt {\frac {(\Theta _{2}-\Theta _{3})(2\Theta _{1}E_{\text{rot}}-L^{2})}{\Theta _{1}\Theta _{2}\Theta _{3}}}}\;,\quad k={\sqrt {{\frac {\Theta _{1}-\Theta _{2}}{\Theta _{2}-\Theta _{3}}}\,{\frac {L^{2}-2\Theta _{3}E_{\text{rot}}}{2\Theta _{1}E_{\text{rot}}-L^{2}}}}}}$

For pericycloidal movements, L²> 2Θ ₂ E is _red and

${\displaystyle {\begin{aligned}\omega _{1}=&{\sqrt {\frac {L^{2}-2\Theta _{3}E_{\text{rot}}}{\Theta _{1}(\Theta _{1}-\Theta _{3})}}}\operatorname {dn} (z;k),&\omega _{2}=&-{\sqrt {\frac {2\Theta _{1}E_{\text{rot}}-L^{2}}{\Theta _{2}(\Theta _{1}-\Theta _{2})}}}\operatorname {sn} (z;k)\\\omega _{3}=&{\sqrt {\frac {2\Theta _{1}E_{\text{rot}}-L^{2}}{\Theta _{3}(\Theta _{1}-\Theta _{3})}}}\operatorname {cn} (z;k),&z=&a(t-t_{0})\end{aligned}}}$

with the frequency a and the elliptical module k

${\displaystyle a={\sqrt {\frac {(\Theta _{1}-\Theta _{2})(L^{2}-2\Theta _{3}E_{\text{rot}})}{\Theta _{1}\Theta _{2}\Theta _{3}}}}\;,\quad k={\sqrt {{\frac {\Theta _{2}-\Theta _{3}}{\Theta _{1}-\Theta _{2}}}\,{\frac {2\Theta _{1}E_{\text{rot}}-L^{2}}{L^{2}-2\Theta _{3}E_{\text{rot}}}}}}}$

Two of the roots of the angular velocities always have the same sign and different signs must appear, which allows a total of six possible combinations, one of which has been selected here at random.

The Euler angles used in the gyroscopic theory are calculated from

${\displaystyle \cos(\vartheta )={\frac {\Theta _{3}}{L}}\omega _{3}\,,\;\tan(\varphi )={\frac {\Theta _{1}\omega _{1}}{\Theta _{2}\omega _{2}}}\,,\;{\dot {\psi }}=L{\frac {2E_{\text{rot}}-\Theta _{3}\omega _{3}^{2}}{L^{2}-\Theta _{3}^{2}\omega _{3}^{2}}}>0}$

In contrast to the force-free symmetrical top, the angular velocities and the angle ϑ between the angular momentum and the 3-axis are not constant. ${\displaystyle \omega _{3},\,{\dot {\psi }},\,{\dot {\varphi }}}$

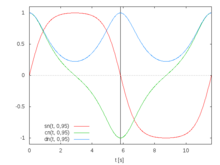
The functions sn and cn are periodic with the period 4 K and dn with the period 2 K , see Fig. 8 , where K is the complete elliptic integral of the first kind :

${\displaystyle K:=\int _{0}^{\frac {\pi }{2}}{\frac {\mathrm {d} \theta }{\sqrt {1-k^{2}\sin ^{2}\theta }}}\,.}$

The angular velocities ω _1,2,3 are thus periodic with the period length ; after this time they return to their original state: ω _1,2,3 (t + T) = ω _1,2,3 (t) . From the periodicity of, it follows that after time T the top is in a position rotated by Δψ . The top only returns to its starting position if Δψ / π is a rational number . ${\displaystyle T={\tfrac {4K}{a}}}$ ${\displaystyle {\dot {\psi }}}$ ${\displaystyle \psi (t+T)-\psi (t)=\Delta \psi ={\text{const.}}}$

The formulas are also valid for symmetrical tops . However, elongated tops with Θ ₁  = Θ ₂  > Θ ₃ can only perform epicycloid rotations and flattened tops with Θ ₁  > Θ ₂  = Θ ₃ only pericycloid rotations, otherwise the amplitude of ω _{2 increases} beyond all limits. For the permitted movements, k  = 0, so that the elliptical functions sn and cn become the harmonic functions sin and cos and dn ≡ 1. Then the local solution changes to that of the symmetrical top.

The only exception to this are force-free spherical gyroscopes , where L² - 2Θ ₃ E _red  = 2Θ ₁ E _red  - L² = 0 and the amplitudes are no longer defined, see # Force-free spherical gyroscope below.

Derivation of the angular velocities according to Euler

The angular velocities are derived from the constants ${\displaystyle L^{2}:=\Theta _{1}^{2}\omega _{1}^{2}+\Theta _{2}^{2}\omega _{2}^{2}+\Theta _{3}^{2}\omega _{3}^{2}\;,\quad E_{\text{rot}}:={\frac {1}{2}}(\Theta _{1}\omega _{1}^{2}+\Theta _{2}\omega _{2}^{2}+\Theta _{3}\omega _{3}^{2})}$ from. For this purpose, Θ 1  >  Θ 2  >  Θ 3 is assumed for the main moments of inertia . With the two constants ω 1 and ω 3 can be expressed as functions of ω 2 : ${\displaystyle \omega _{1}^{2}={\frac {\Theta _{2}(\Theta _{2}-\Theta _{3})}{\Theta _{1}(\Theta _{1}-\Theta _{3})}}(x_{1}^{2}-\omega _{2}^{2})\;,\quad \omega _{3}^{2}={\frac {\Theta _{2}(\Theta _{1}-\Theta _{2})}{\Theta _{3}(\Theta _{1}-\Theta _{3})}}(x_{2}^{2}-\omega _{2}^{2})}$     (*)   With ${\displaystyle {\begin{aligned}x_{1}:={\sqrt {\frac {L^{2}-2\Theta _{3}E_{\text{rot}}}{\Theta _{2}(\Theta _{2}-\Theta _{3})}}}\;,\quad x_{2}:={\sqrt {\frac {2\Theta _{1}E_{\text{rot}}-L^{2}}{\Theta _{2}(\Theta _{1}-\Theta _{2})}}}\\x_{1}^{2}-x_{2}^{2}={\frac {(\Theta _{1}-\Theta _{3})(L^{2}-2\Theta _{2}E_{\text{rot}})}{\Theta _{2}(\Theta _{1}-\Theta _{2})(\Theta _{2}-\Theta _{3})}}\end{aligned}}}$ Because the terms are positive, it follows ${\displaystyle -1\leq {\frac {\omega _{2}}{x_{1,2}}}\leq 1}$ The second of Euler's gyroscopic equations with the above ω gives 1,2 ${\displaystyle {\dot {\omega }}_{2}=x_{3}{\sqrt {(x_{1}^{2}-\omega _{2}^{2})(x_{2}^{2}-\omega _{2}^{2})}}\;,\quad x_{3}:={\sqrt {\frac {(\Theta _{1}-\Theta _{2})(\Theta _{2}-\Theta _{3})}{\Theta _{1}\Theta _{3}}}}}$ In epicyclic movements and the solution obtained with ω 2 (t 0 )  = 0, which is away from the second major axis always arrives sometime after separation of variables and the substitution q = x 1 sin (θ) to ${\displaystyle L^{2}<2\Theta _{2}E_{\text{rot}},\,x_{1}^{2}<x_{2}^{2}}$ ${\displaystyle x_{2}x_{3}\int _{t_{0}}^{t}\mathrm {d} \tau =\int _{0}^{\omega _{2}}{\frac {x_{2}\mathrm {d} q}{\sqrt {(x_{1}^{2}-q^{2})(x_{2}^{2}-q^{2})}}}=\int _{0}^{\varphi }{\frac {\mathrm {d} \vartheta }{\sqrt {1-k^{2}\sin ^{2}(\vartheta )}}}}$ On the right side there is an elliptic integral of the 1st kind with the elliptic module k = x 1 / x 2 , which has a Jacobian elliptic function as solution function: ${\displaystyle {\begin{aligned}\operatorname {sn} {\Bigg (}\int _{0}^{\varphi }{\frac {\mathrm {d} \vartheta }{\sqrt {1-k^{2}\sin ^{2}(\vartheta )}}};k{\Bigg )}:=&\sin(\varphi )={\frac {\omega _{2}}{x_{1}}}\\\rightarrow \omega _{2}=x_{1}\operatorname {sn} \left(x_{2}x_{3}\int _{t_{0}}^{t}\mathrm {d} \tau ;k\right)=&x_{1}\operatorname {sn} {\big (}x_{2}x_{3}(t-t_{0});k{\big )}\end{aligned}}}$ From (*) ω 1 and ω 3 can now be calculated with the help of the relationships between the squared Jacobian elliptic functions with the result given in the text. With pericycloidal movement is and the result is derived with exchanged x 1.2 . ${\displaystyle L^{2}>2\Theta _{2}E_{\text{rot}},\,x_{1}^{2}>x_{2}^{2}}$

Derivation of the Euler angles

Comparison of the components of the angular momentum in Euler angles (see centrifugal theory # reference systems and Euler angles ) provides the principal axes system ê 1,2,3 : ${\displaystyle {\begin{aligned}{\vec {L}}=&L{\hat {e}}_{z}=L{\begin{pmatrix}\sin(\vartheta )\sin(\varphi )\\\sin(\vartheta )\cos(\varphi )\\\cos(\vartheta )\end{pmatrix}}={\begin{pmatrix}L_{1}\\L_{2}\\L_{3}\end{pmatrix}}={\begin{pmatrix}\Theta _{1}\omega _{1}\\\Theta _{2}\omega _{2}\\\Theta _{3}\omega _{3}\end{pmatrix}}\\\rightarrow \cos(\vartheta )=&{\frac {L_{3}}{L}}={\frac {\Theta _{3}\omega _{3}}{L}}\;,\quad \tan(\varphi )={\frac {L_{1}}{L_{2}}}={\frac {\Theta _{1}\omega _{1}}{\Theta _{2}\omega _{2}}}\end{aligned}}}$ The angle ψ is determined with from ${\displaystyle L_{1}^{2}+L_{2}^{2}=\Theta _{1}^{2}\omega _{1}^{2}+\Theta _{2}^{2}\omega _{2}^{2}=L^{2}\sin ^{2}(\vartheta )}$ ${\displaystyle {\begin{aligned}{\vec {\omega }}=&{\begin{pmatrix}\omega _{1}\\\omega _{2}\\\omega _{3}\end{pmatrix}}={\begin{pmatrix}{\dot {\psi }}\sin(\vartheta )\sin(\varphi )+{\dot {\vartheta }}\cos(\varphi )\\{\dot {\psi }}\sin(\vartheta )\cos(\varphi )-{\dot {\vartheta }}\sin(\varphi )\\{\dot {\psi }}\cos(\vartheta )+{\dot {\varphi }}\end{pmatrix}}\\\rightarrow {\dot {\psi }}=&{\frac {\omega _{1}\sin(\varphi )+\omega _{2}\cos(\varphi )}{\sin(\vartheta )}}=L{\frac {\omega _{1}\overbrace {L\sin(\vartheta )\sin(\varphi )} ^{L_{1}=\Theta _{1}\omega _{1}}+\omega _{2}\overbrace {L\sin(\vartheta )\cos(\varphi )} ^{L_{2}=\Theta _{2}\omega _{2}}}{L^{2}\sin ^{2}(\vartheta )}}\\=&L{\frac {\Theta _{1}\omega _{1}^{2}+\Theta _{2}\omega _{2}^{2}}{\Theta _{1}^{2}\omega _{1}^{2}+\Theta _{2}^{2}\omega _{2}^{2}}}=L{\frac {2E_{\text{rot}}-\Theta _{3}\omega _{3}^{2}}{L^{2}-\Theta _{3}^{2}\omega _{3}^{2}}}\end{aligned}}}$

Movement on the Separatrix

Fig. 9: Path of a point on the 2-axis (red) around the angular momentum axis (vertical line) along a loxodrome

On the separatrix, 2Θ ₂ E _rot = L ² and the movement is aperiodic, because the angular velocity does not assume a state a second time. The movement of the gyroscope is characterized here by the fact that the plane spanned by the 2-axis and the angular momentum circles around the angular momentum axis at a constant angular velocity L / Θ ₂ and the end point of the 2-axis is on a loxodrome with the directional angle

${\displaystyle \cos \eta ={\sqrt {\frac {(\Theta _{1}-\Theta _{2})(\Theta _{2}-\Theta _{3})}{\Theta _{2}(\Theta _{1}+\Theta _{3}-\Theta _{2})}}}}$

approaches the axis defined by the angular momentum, see Fig. 9.

The formulas of the previous section are valid here, but because the elliptical module is the extreme value

${\displaystyle k={\sqrt {{\frac {\Theta _{1}-\Theta _{2}}{\Theta _{2}-\Theta _{3}}}\,{\frac {L^{2}-2\Theta _{3}E_{\text{rot}}}{2\Theta _{1}E_{\text{rot}}-L^{2}}}}}={\sqrt {{\frac {\Theta _{1}-\Theta _{2}}{\Theta _{2}-\Theta _{3}}}\,{\frac {2\Theta _{2}E_{\text{rot}}-2\Theta _{3}E_{\rm {rot}}}{2\Theta _{1}E_{\rm {rot}}-2\Theta _{2}E_{\text{rot}}}}}}=1}$

assumes, the elliptic functions go into the aperiodic hyperbolic functions :

${\displaystyle \operatorname {cn} (z;1)=\operatorname {dn} (z;1)={\frac {1}{\cosh(z)}}}$ and ${\displaystyle \operatorname {sn} (z;1)=\tanh(z)}$

The argument z and the angular velocities of the previous section specialize in:

${\displaystyle {\begin{aligned}z=&{\sqrt {\frac {(\Theta _{2}-\Theta _{3})(2\Theta _{1}E_{\text{rot}}-L^{2})}{\Theta _{1}\Theta _{2}\Theta _{3}}}}(t-t_{0})\\=&{\sqrt {\frac {(\Theta _{1}-\Theta _{2})(\Theta _{2}-\Theta _{3})}{\Theta _{1}\Theta _{3}}}}{\frac {L}{\Theta _{2}}}(t-t_{0})\\\omega _{1}=&{\sqrt {\frac {L^{2}-2\Theta _{3}E_{\text{rot}}}{\Theta _{1}(\Theta _{1}-\Theta _{3})}}}\operatorname {cn} (z;k)={\sqrt {\frac {\Theta _{2}(\Theta _{2}-\Theta _{3})}{\Theta _{1}(\Theta _{1}-\Theta _{3})}}}{\frac {L}{\Theta _{2}\cosh(z)}}\\\omega _{2}=&{\sqrt {\frac {L^{2}-2\Theta _{3}E_{\text{rot}}}{\Theta _{2}(\Theta _{2}-\Theta _{3})}}}\operatorname {sn} (z;k)={\frac {L}{\Theta _{2}}}\tanh(z)\\\omega _{3}=&{\sqrt {\frac {2\Theta _{1}E_{\text{rot}}-L^{2}}{\Theta _{3}(\Theta _{1}-\Theta _{3})}}}\operatorname {dn} (z;k)={\sqrt {\frac {\Theta _{2}(\Theta _{1}-\Theta _{2})}{\Theta _{3}(\Theta _{1}-\Theta _{3})}}}{\frac {L}{\Theta _{2}\cosh(z)}}\end{aligned}}}$

As time goes on, ω ₁ and ω ₃ tend to zero and ω ₂ to L / Θ ₂ . The movement comes as close as desired to a rotation around the 2-axis without ever reaching this state. In reality, this form of movement will hardly occur, because with the smallest deviation from the ideal case 2Θ ₂ E _rot = L ², k ≠ 1 and the angular velocities become the periodic ones of the previous section. The movement on the separatrix is ​​unstable. A movement near the separatrix shows the Dschanibekow effect .

Fig. 10: Basic system and meridian used ( ψ = α , ϑ = β and φ = γ ). ${\displaystyle {\hat {h}}_{1,2,3}}$ ${\displaystyle {\hat {m}}}$

In contrast to the previous section, the approach for the local base system is used to calculate the movement , see Fig. 10 and cf. Fig. 2 . ${\displaystyle {\hat {h}}_{1,2,3}={\hat {e}}_{Y,Z,X}}$

The Euler angles - see #movement function of the symmetrical top - result from angular momentum in the z-direction and a start with ω ₂  = 0

${\displaystyle {\begin{aligned}{\dot {\psi }}=&{\frac {L}{\Theta _{2}}}\\\cos(\vartheta )=&\tanh(z)\\\tan(\varphi )=&{\sqrt {\frac {\Theta _{3}(\Theta _{1}-\Theta _{2})}{\Theta _{1}(\Theta _{2}-\Theta _{3})}}}\,.\end{aligned}}}$

The plane spanned by the 2-axis and the angular momentum circles around the angular momentum axis at a constant angular velocity L / Θ ₂ and the angle ϑ tends to zero with increasing time.

proof

In the basic system ${\displaystyle {\begin{aligned}{\hat {h}}_{1}=&{\hat {e}}_{Y}={\hat {e}}_{2}={\begin{pmatrix}-\cos(\psi )\sin(\varphi )-\sin(\psi )\cos(\vartheta )\cos(\varphi )\\-\sin(\psi )\sin(\varphi )+\cos(\psi )\cos(\vartheta )\cos(\varphi )\\\sin(\vartheta )\cos(\varphi )\end{pmatrix}}\\{\hat {h}}_{2}=&{\hat {e}}_{Z}={\hat {e}}_{3}={\begin{pmatrix}\sin(\psi )\sin(\vartheta )\\-\cos(\psi )\sin(\vartheta )\\\cos(\vartheta )\end{pmatrix}}\\{\hat {h}}_{3}=&{\hat {e}}_{X}={\hat {e}}_{1}={\begin{pmatrix}\cos(\psi )\cos(\varphi )-\sin(\psi )\cos(\vartheta )\sin(\varphi )\\\sin(\psi )\cos(\varphi )+\cos(\psi )\cos(\vartheta )\sin(\varphi )\\\sin(\vartheta )\sin(\varphi )\end{pmatrix}}\end{aligned}}}$ surrendered: ${\displaystyle {\begin{aligned}{\vec {L}}=&L{\hat {e}}_{z}=L{\begin{pmatrix}\sin(\vartheta )\cos(\varphi )\\\cos(\vartheta )\\\sin(\vartheta )\sin(\varphi )\end{pmatrix}}_{{\hat {h}}_{i}}={\begin{pmatrix}L_{1}\\L_{2}\\L_{3}\end{pmatrix}}_{{\hat {h}}_{i}}={\begin{pmatrix}\Theta _{1}\omega _{1}\\\Theta _{2}\omega _{2}\\\Theta _{3}\omega _{3}\end{pmatrix}}_{{\hat {h}}_{i}}\\\rightarrow \cos(\vartheta )=&{\frac {L_{2}}{L}}={\frac {\Theta _{2}\omega _{2}}{L}}={\frac {\Theta _{2}}{L}}{\frac {L}{\Theta _{2}}}\tanh(z)=\tanh(z)\\\tan(\varphi )=&{\frac {L_{3}}{L_{1}}}={\frac {\Theta _{3}}{\Theta _{1}}}{\frac {\omega _{3}}{\omega _{1}}}={\frac {\Theta _{3}}{\Theta _{1}}}{\frac {{\sqrt {\frac {\Theta _{1}-\Theta _{2}}{\Theta _{2}\Theta _{3}(\Theta _{1}-\Theta _{3})}}}{\frac {L}{\cosh(z)}}}{{\sqrt {\frac {\Theta _{2}-\Theta _{3}}{\Theta _{1}\Theta _{2}(\Theta _{1}-\Theta _{3})}}}{\frac {L}{\cosh(z)}}}}={\sqrt {\frac {\Theta _{3}(\Theta _{1}-\Theta _{2})}{\Theta _{1}(\Theta _{2}-\Theta _{3})}}}\end{aligned}}}$ With the new basic system, the components of angular velocity are: ${\displaystyle {\begin{aligned}{\vec {\omega }}=&[{\dot {\psi }}\sin(\vartheta )\sin(\varphi )+{\dot {\vartheta }}\cos(\varphi )]{\hat {e}}_{1}+[{\dot {\psi }}\sin(\vartheta )\cos(\varphi )-{\dot {\vartheta }}\sin(\varphi )]{\hat {e}}_{2}\\&+[{\dot {\psi }}\cos(\vartheta )+{\dot {\varphi }}]{\hat {e}}_{3}\\=&[\underbrace {{\dot {\psi }}\sin(\vartheta )\sin(\varphi )+{\dot {\vartheta }}\cos(\varphi )} _{\omega _{3}}]{\hat {h}}_{3}+[\underbrace {{\dot {\psi }}\sin(\vartheta )\cos(\varphi )-{\dot {\vartheta }}\sin(\varphi )} _{\omega _{1}}]{\hat {h}}_{1}\\&+[\underbrace {{\dot {\psi }}\cos(\vartheta )+{\dot {\varphi }}} _{\omega _{2}}]{\hat {h}}_{2}\,.\end{aligned}}}$ The angular velocity can now be determined with from ${\displaystyle {\dot {\psi }}}$ ${\displaystyle {\dot {\varphi }}=0}$ ${\displaystyle \omega _{2}={\dot {\psi }}\cos(\vartheta )+{\dot {\varphi }}={\dot {\psi }}\cos(\vartheta )}$ ${\displaystyle {\dot {\psi }}={\frac {\omega _{2}}{\cos(\vartheta )}}={\frac {{\frac {L}{\Theta _{2}}}\tanh(z)}{\tanh(z)}}={\frac {L}{\Theta _{2}}}\,.}$ The axis around which the angle ϑ rotates and the meridian thus has the direction ${\displaystyle {\hat {u}}_{\vartheta }=\cos(\varphi ){\hat {h}}_{3}-\sin(\varphi ){\hat {h}}_{1}}$ ${\displaystyle {\hat {m}}={\hat {h}}_{2}\times {\hat {u}}_{\vartheta }=\cos(\varphi ){\hat {h}}_{1}+\sin(\varphi ){\hat {h}}_{3}\,.}$ The rate of the 2 axis is ${\displaystyle {\dot {\hat {h}}}_{2}={\vec {\omega }}\times {\hat {h}}_{2}=\omega _{1}{\hat {h}}_{3}-\omega _{3}{\hat {h}}_{1}\,.}$ With the above intermediate results and the trigonometric formulas , the direction angle between the meridian and the rate of the 2-vector to the constant is calculated ${\displaystyle {\begin{aligned}\cos \eta =&{\frac {{\dot {\hat {h}}}_{2}\cdot {\hat {m}}}{|{\dot {\hat {h}}}_{2}||{\hat {m}}|}}={\frac {\omega _{1}\sin(\varphi )-\omega _{3}\cos(\varphi )}{\sqrt {\omega _{1}^{2}+\omega _{3}^{2}}}}={\frac {\left[\tan(\varphi )-{\frac {\omega _{3}}{\omega _{1}}}\right]\cos(\varphi )}{\sqrt {1+{\frac {\omega _{3}^{2}}{\omega _{1}^{2}}}}}}\\=&{\frac {\tan(\varphi )-{\frac {\Theta _{1}}{\Theta _{3}}}\tan(\varphi )}{{\sqrt {1+{\frac {\Theta _{1}^{2}}{\Theta _{3}^{2}}}\tan ^{2}(\varphi )}}{\sqrt {1+\tan ^{2}(\varphi )}}}}={\sqrt {\frac {(\Theta _{1}-\Theta _{2})(\Theta _{2}-\Theta _{3})}{\Theta _{2}(\Theta _{1}+\Theta _{3}-\Theta _{2})}}}\end{aligned}}}$ The fraction in the root is positive and less than one: ${\displaystyle 0<{\frac {(\Theta _{1}-\Theta _{2})(\Theta _{2}-\Theta _{3})}{\Theta _{2}(\Theta _{1}+\Theta _{3}-\Theta _{2})}}=1-{\frac {\Theta _{1}\Theta _{3}}{\Theta _{2}(\Theta _{1}+\Theta _{3}-\Theta _{2})}}<1}$

Force-free spherical top

Spherical top have three equal principal moments of inertia , bringing the #Kreiselgleichungen to

${\displaystyle \Theta _{1}{\dot {\omega }}_{1}=\Theta _{2}{\dot {\omega }}_{2}=\Theta _{3}{\dot {\omega }}_{3}={\dot {L}}_{1}={\dot {L}}_{2}={\dot {L}}_{3}=0}$

simplify. With the force-free spherical top, the angular velocity and angular momentum are parallel, constant and body-fixed.

Influence of friction

The power-free top is an idealization that can only be approximated under the conditions on earth. On the one hand, frictional moments inevitably occur in the bearings that hold the gyroscope against the force of weight , and the sticking condition of the air on solid surfaces leads to a slowing interaction with the ambient air.

The influence of friction in the cardanic suspension, as in Fig. 1 , is noticeable differently in the symmetrical top, depending on whether it is stretched or flattened:

• With an extended top, the angle of inclination ϑ increases compared to the angular momentum and the figure axis becomes an unstable axis of rotation.
• With a flattened top, the angle of inclination ϑ decreases and the figure axis remains a stable axis of rotation.

Both gyroscope shapes have in common that the intrinsic speed of rotation ω ₃ decreases over time.

Air friction also slows down the speed of rotation and has different effects on elongated or flattened tops:

• In the case of an extended top, the axis of rotation becomes increasingly perpendicular to the figure axis, which here too becomes an unstable axis of rotation.
• With the flattened top, the speed of rotation moves towards the figure axis, which remains a stable axis of rotation.

See also

• Inertial ellipsoid provides information on inertial, energy and swirl ellipsoid

Individual evidence

1. ↑ Euler (1758), pp. 173 and 190.
2. ↑ Leimanis (1965), p. 53 ff.
3. ↑ Magnus (1971), p. 100
4. ^ Arnold (1989), p. 154
5. ^ Arnold (1989), p. 142, Magnus (1971), p. 53, Leimanis (1965), p. 10.
6. ^ Arnold (1989), p. 151.
7. ↑ Leimanis (1965), p. 11.
8. ^ Samuel Haughton: On the Rotation of a Solid Body Round a Fixed Point; Being an Account of the Late Professor Mac Cullagh's Lectures on That Subject . In: Royal Irish Academy (Ed.): The Transactions of the Royal Irish Academy . Vol. 22 (1849). Dublin university press, Dublin 1880, p. 139–154 , JSTOR : 30079824 (English, Haughton's transcript of a lecture from 1844. See also Magnus (1971), pp. 61ff.).
9. ↑ Magnus (1971), p. 82.
10. ↑ ^{a b} Grammel (1920), p. 40, Grammel (1950), p. 53.
11. ^ Louis Poinsot : Théorie nouvelle de la rotation des corps. Bachelier, Paris 1834/1851.
12. ↑ tennis racket theorem in the English language Wikipedia.
13. ↑ Mark S. Ashbaugh, Carmen C. Chicone, Richard H. Cushman: The twisting tennis racket. In: Journal of Dynamics and Differential Equations , 3, 1, 1991, pp. 67-85.
14. ↑ ^{a b} Magnus (1971), p. 64ff.
15. ↑ Leimanis (1965), p. 17.
16. ↑ Leimanis (1965), p. 18.
17. ↑ Grammel (1920), p. 82 ff., Grammel (1950), p. 107 ff.

literature

• Leonhard Euler : About the movement of the rotation of rigid bodies around a variable axis . In: Royal Prussian Academy of Sciences in Berlin (ed.): Mémoires de l'Académie des Sciences de Berlin . tape 14 . Petersburg 1758, p. 173 and 190 . (French, archive.org [accessed on January 11, 2020] Original title: Du mouvement de rotation des corps solides autour d'un ax variable .).
• Herbert Goldstein, Charles P. Poole, Jr, John L. Safko: Classical Mechanics . 3. Edition. Wiley-VCH, Weinheim 2006, ISBN 3-527-40589-5 .
• R. Grammel : The top . Its theory and its applications. Vieweg Verlag, Braunschweig 1920 DNB  573 533 210 ( archive.org - "swing" means angular momentum, " rotational shock " about the torque and "rotational force" rotational energy, see p VII). or R. Grammel : The top . Theory of the gyro. 2. revised Edition volume
  
   1 . Springer, Berlin, Göttingen, Heidelberg 1950, DNB  451641299 .
• VI Arnold: Mathematical Methods of Classical Mechanics . 2nd Edition. Springer, New-York / Berlin / Heidelberg / London / Paris / Tokyo 1989, ISBN 3-540-96890-3 .
• K. Magnus: Top . Theory and applications. Springer, Berlin / Heidelberg / New York 1971, ISBN 978-3-642-52163-8 ( limited preview in Google Book Search [accessed January 5, 2020]).
• Eugene Leimanis: The General Problem of the Motion of Coupled Rigid Bodies about a Fixed Point . Springer Verlag, Berlin, Heidelberg 1965, ISBN 978-3-642-88414-6 , p. 10 ff ., doi : 10.1007 / 978-3-642-88412-2 (English, limited preview in Google Book Search [accessed November 30, 2019]).

Web links

• Interactive animations of gyroscopic and pendulum movements .
• Free rotation of a cuboid body from the TIB AV portal of the technical information library .