Regular precession

Fig. 1: Regular precession of a symmetrical top

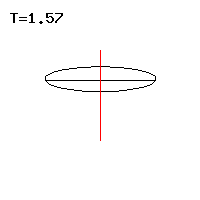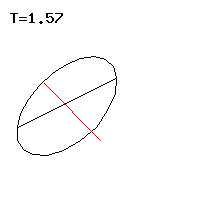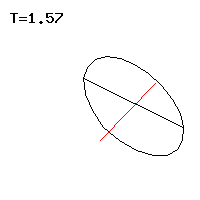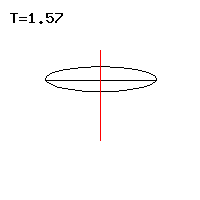
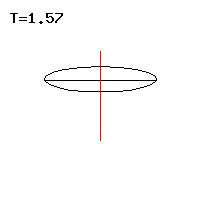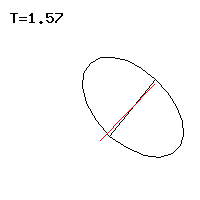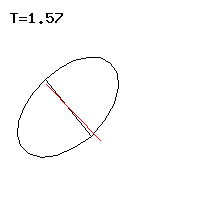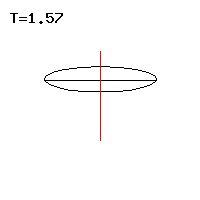
In regular precession , a top rotates at a constant angular speed around a fixed precession axis and an axis fixed to the body, which enclose a constant angle, see animation in Fig. 1.

In symmetrical gyroscopes as in the animation and in Grioli's precession in Fig. 8, the axis fixed to the body is orthogonal to a circular section plane of the ellipsoid of inertia of the top. With the Staude rotations , the fixed axis and the fixed axis coincide and are perpendicular . The regular precession of the symmetrical top is the gyro-theoretical analogue to the circular motion of a mass point due to a central force , see #Mechanical Interpretation .

Dissipative friction effects and uniform rotations around the vertical axis of the figure of symmetrical tops are to be looked up at the Euler top and Lagrange top .

The regular precession is an important point in the gyroscopic theory , not least because the earth's rotation resembles a regular precession, whereby deviations from the theory occur due to the deformability and fluctuating mass distribution of the earth's body.

Regular precession of symmetrical tops

Every otherwise force-free gyro can be forced to any regular precessions by means of suitable torques . The resistance of the top is expressed as a gyroscopic effect , which in the case of a symmetrical heavy top can be in dynamic equilibrium with the moment of weight , if the rotation around the figure axis, the precession speed μ and the inclination of the top according to

${\displaystyle F_{g}s=\mu L_{f}}$

are matched to its mass distribution. In it is

• F _{g is} the weight ,
• s is the distance of the center of mass from the point of contact and
• L _{f is} the axial component of the angular momentum.

Forced regular precession of symmetrical tops

A symmetrical top should rotate with constant angular velocity around the vertical, space-fixed precession axis ê _z and with constant angular velocity ν  : =  around the body-fixed figure axis ê ₃ , which includes the constant angle of inclination ϑ with ê _z (for terms see gyro theory # reference systems and Euler angles . ) For a gyroscope with axial moment of inertia C and equatorial A , accordingly ${\displaystyle \mu :={\dot {\psi }}}$ ${\displaystyle {\dot {\varphi }}}$

${\displaystyle {\begin{aligned}{\vec {\omega }}=&\mu {\hat {e}}_{z}+\nu {\hat {e}}_{3}=\mu ({\hat {e}}_{z}-u{\hat {e}}_{3})+(\mu u+\nu ){\hat {e}}_{3}\\{\vec {L}}=&A\mu ({\hat {e}}_{z}-u{\hat {e}}_{3})+C(\mu u+\nu ){\hat {e}}_{3}=L_{\textsf {v}}{\hat {e}}_{z}+L_{f}{\hat {e}}_{3}\\L_{\textsf {v}}=&A\mu \\L_{f}=&(C-A)\mu u+C\nu \end{aligned}}}$

with u: = cos (ϑ) = ê _z  ‧ ê ₃ . As with the nutation of a force-free Euler top , the angular velocity, the angular momentum, the precession axis and the figure axis lie in one plane, the precession plane , only with the forced precession angular momentum and precession axis do not coincide.

Condition on the angular momentum

Fig. 2: Couple of forces consisting of weight F _g and oppositely equal contact force - F _g with regularly precessing top.

The rotation of the angular momentum results in a gyroscopic effect that can only be dynamically balanced if the torque of the weight force is required.

The gyroscopic effect can be seen directly from the forced regular precession of a spherical top with A = C and identical angular momentum. Since the angular momentum coincides, but not the moments of inertia, the spherical top precesses with other angular velocities μ _k , ν _k :

${\displaystyle {\begin{aligned}{\vec {L}}=&A\mu _{k}{\hat {e}}_{z}+[(A-A)\mu _{k}u+A\nu _{k}]{\hat {e}}_{3}\\=&A\mu _{k}{\hat {e}}_{z}+A\nu _{k}{\hat {e}}_{3}\;{\stackrel {!}{=}}\;L_{\textsf {v}}{\hat {e}}_{z}+L_{f}{\hat {e}}_{3}\end{aligned}}}$

From this Aμ _k  = Aμ = L _v and Aν _k  = L _{f can be} read off. The gyroscopic effect is inversely equal to the speed of the angular momentum, which is equal to that of the axial angular momentum L _f , which in the spherical top with μ _k  = μ circles around ê _z :

${\displaystyle {\vec {K}}=-{\dot {\vec {L}}}=-(\mu {\hat {e}}_{z})\times (L_{f}{\hat {e}}_{3})=-\mu L_{f}{\hat {e}}_{z}\times {\hat {e}}_{3}}$

This is analogous to where the speed for a pure rotation at angular speed results from the cross product “×” with the distance to a fixed point on the axis of rotation. The gyroscopic action depends only on the angular momentum and its time derivative and is therefore the same for the symmetrical top with A ≠ C as that of the spherical top . ${\displaystyle {\vec {v}}={\vec {\omega }}\times {\vec {r}}}$ ${\displaystyle {\vec {v}}}$ ${\displaystyle {\vec {\omega }}}$ ${\displaystyle {\vec {r}}}$

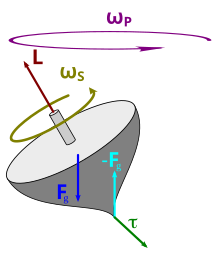
The weight F _g and the opposing, equal contact force form, as shown in Fig. 2, a force couple that corresponds to the moment of gravity . It is only parallel to the gyroscopic action if the center of mass lies in the precession plane , but the first component ρê _z does not take part in any self- rotation around the figure axis, which is the case with the game top in Fig. 3 and the # Staude rotations of symmetrical tops . The moment of gravity is then: ${\displaystyle {\vec {M}}:={\vec {s}}\times (-F_{g}{\hat {e}}_{z})}$ ${\displaystyle {\vec {s}}=\rho {\hat {e}}_{z}+s{\hat {e}}_{3}}$

${\displaystyle {\vec {M}}:=(\rho {\hat {e}}_{z}+s{\hat {e}}_{3})\times (-F_{g}{\hat {e}}_{z})=F_{g}s{\hat {e}}_{z}\times {\hat {e}}_{3}}$

According to the law of swirl , this moment is able to maintain a regular precession if moment and gyroscopic action are in dynamic equilibrium , the at ${\displaystyle {\vec {M}}+{\vec {K}}={\vec {0}}}$

${\displaystyle F_{g}s=\mu L_{f}}$

entry. This result concerns

Fig. 3: Play top with a spherical top with radius ρ around the center K at a distance s from the center of mass G.

Lagrange top

Here the support point is the reference point for the weight moment, the mass moments of inertia and the angular momentum. If the lower tip of the top is spherical with a considerable radius ρ, the reference point is in the center K of the sphere, see Fig. 3.

Symmetrical game top

The supporting moment F _g s is the same as with the Lagrange top, only the center of mass is the reference point here. Under the influence of sliding friction , the gyroscope takes on a vertical position over time or falls into a regular precession, in which the round lower tip of the gyroscope rolls without slipping on the ground.

Symmetrical Euler tops

Here the angular momentum is constant and neither a weight nor a gyroscopic effect occurs. Correspondingly, F _g s = L _f  = 0 and the constant angular momentum points in the direction of the precession axis ê _z , which is less of a restriction for the angular momentum than of the prerequisite for the force-free top to appear as a special case. The component L _v is equal to the amount L of the angular momentum, which is the hypotenuse of a right-angled triangle , and the axial angular momentum L ₃  =  L  cos (ϑ) forms the adjacent to the inclination angle ϑ of the figure axis in the triangle.

Constants of motion

In the angular momentum and the angular velocity, only the figure axis ê _{3 is} time-dependent: The figure axis rotates with constant inclination around the precession axis ê _z . In addition to the given μ and ν, the angular velocities cannot be changed

${\displaystyle {\begin{aligned}r:=&{\vec {\omega }}\cdot {\hat {e}}_{3}\!\!\!\!\!\!\!\!\!\!\!\!&=&\mu u+\nu \\\omega _{z}:=&{\vec {\omega }}\cdot {\hat {e}}_{z}\!\!\!\!\!\!\!\!\!\!\!\!&=&\mu +\nu u\\\omega :=&|{\vec {\omega }}|\!\!\!\!\!\!\!\!\!\!\!\!&=&{\sqrt {\mu ^{2}+2\mu \nu u+\nu ^{2}}}\end{aligned}}}$

the angular momentum already given above

${\displaystyle {\begin{aligned}L_{\textsf {v}}=&A\mu \\L_{f}=&C(\mu u+\nu )-A\mu u\end{aligned}}}$

such as

${\displaystyle {\begin{aligned}L_{3}:=&{\vec {L}}\cdot {\hat {e}}_{3}\!\!\!\!\!\!\!\!\!\!\!\!&=&L_{\textsf {v}}u+L_{f}=C(\mu u+\nu )\\L_{z}:=&{\vec {L}}\cdot {\hat {e}}_{z}\!\!\!\!\!\!\!\!\!\!\!\!&=&L_{\textsf {v}}+L_{f}u=A\mu (1-u^{2})+L_{3}u\\L:=&|{\vec {L}}|\!\!\!\!\!\!\!\!\!\!\!\!&=&{\sqrt {L_{\textsf {v}}^{2}+2L_{\textsf {v}}L_{f}u+L_{f}^{2}}}\end{aligned}}}$

and the rotational , positional and total energy

${\displaystyle {\begin{aligned}E_{\text{rot}}:=&{\frac {1}{2}}{\vec {\omega }}\cdot {\vec {L}}\!\!\!\!\!\!\!\!\!\!\!\!&=&{\frac {1}{2}}{\big (}A\mu ^{2}(1-u^{2})+C(\mu u+\nu )^{2}{\big )}\\E_{\text{pot}}:=&(\rho {\hat {e}}_{z}+s{\hat {e}}_{3})\cdot (F_{g}{\hat {e}}_{z})\!\!\!\!\!\!\!\!\!\!\!\!&=&(\rho +su)F_{g}\\E_{\text{ges}}:=&E_{\text{rot}}+E_{\text{pot}}\!\!\!\!\end{aligned}}}$

because they can be expressed with applied constants μ, ν and u  = cos (ϑ). The positional energy is equal to the work of the weight F _g along the perpendicular path ρ + su , and “·” forms the scalar product .

Mechanical interpretation

With the heavy top it seems paradoxical that it does not give in to the force of weight and increases the angle of inclination ϑ, as it would in a state of rest, but instead deviates perpendicular to the force. This is explained by the rule of parallelism in the same direction , according to which the gyroscope tries to align its angular momentum in the same direction parallel to the direction of rotation of the moment. The moment works horizontally, which clears up this paradox. The figure axis rather begins to incline towards the node axis ê _z  × ê ₃ and does not come closer to it only because the moment of gravity continues to rotate in the same sense.

This behavior is similar to the circular motion of a mass point around a center, maintained by a centripetal force :

• Just as the figure axis of the top does not come closer to the node axis, which is the same as the direction of the gravitational moment, so does the rotating mass point no closer to the center of force.
• The centripetal force, like the moment of gravity in a gyroscope, must have a size that is matched to the speed.
• Just as the centripetal force does little work and increases the energy of the mass point, the moment of gravity does not do any work in the top and the energy content of the top is retained.
• The centripetal force alone cannot initiate the circular motion; this requires a tangential impact on the stationary mass point corresponding to the distance from the center . Likewise, the top rotating uniformly around its axis of the figure must receive a well- measured rotary thrust perpendicular to the axis of the figure , so that a regular precession begins.

Precession speeds

Because L _f  = (C - A) μu + Cν depends on μ, the #condition on the angular momentum μL _f  = F _g s results in a quadratic equation

${\displaystyle (C-A)u\mu ^{2}+C\nu \mu -F_{g}s=0}$

with the solutions:

${\displaystyle {\begin{aligned}(C-A)u=0:&\quad \mu ={\frac {F_{g}s}{C\nu }}\\(C-A)u\neq 0:&\quad \mu _{1,2}={\frac {-C\nu }{2(C-A)u}}\left(1\pm {\sqrt {1+{\frac {4(C-A)F_{g}su}{C^{2}\nu ^{2}}}}}\right)\end{aligned}}}$

General case

• Regular precessions of an upright straight top
• 

  Fig. 4: Fast regular precession

• 

  Fig. 5: Slow regular precession

A distinction must be made between the following cases for the straight top (C <A):

• 0 ° <ϑ <90 °, 1> u = cos (ϑ)> 0: Upright, elongated top whose precession is in the same direction as it rotates when viewed from above:
  • C² ν² <| 4 (C - A) F _g s u |: A regular precession is not possible.
  • C² ν² = | 4 (C - A) F _g s u |: There is a precession velocity.
  • C² ν²> | 4 (C - A) F _g s u |: There are two precession speeds, see Fig. 4 and 5.
• ϑ = 90 °, u = 0: Horizontal figure axis, there is a precession in the same direction as the self-rotation, which obeys the condition C μ ν = F _g s.
• 90 ° <ϑ <180 °, 0> u> -1: Hanging elongated top that can assume two precession speeds with different signs. With the faster, precession and self-rotation are seen from above in the same direction, with the slower they are opposite.

In the formula for the speed of precession, C - A and u appear only as a product (C - A) u, which is why the hanging elongated top with u, C - A <0 behaves in a similar way to the upright flattened top with u, C - A> 0 and the hanging flattened as well as the upright stretched one:

“The regular precessions of the extended, raised gyroscope are seen from above in the same sense as the rotation of the gyroscope, those of the flattened, lowered gyroscope in the opposite sense, and they are only possible with both gyroscopes if the intrinsic speed of rotation ν is sufficiently high.

With the extended, lowered top, the faster of the two regular precessions, viewed from above, occurs in the direction of the top rotation, the slower in the opposite direction, and with the flattened, lifted top, it is just the other way round, but no minimum value of the intrinsic rotational speed ν is required for both tops. "

- R. Grammel

The following special cases are noteworthy.

Fast gyro

With the fast gyro, where C² ν² ≫ 4 | (C - A) F _g s u | the approximation applies with u = cos (ϑ)

${\displaystyle {\begin{aligned}(C-A)u=0:&\quad \mu ={\frac {F_{g}s}{C\nu }}\\(C-A)u\neq 0:&\quad \mu _{1,2}\approx {\begin{cases}{\frac {-C\nu }{(C-A)u}}&(1)\\{\frac {F_{g}s}{C\nu }}&(2)\end{cases}}\end{aligned}}}$

With slow precession (2) the precession speed is in the same direction and inversely proportional to the rotation ν and also independent of the angle of inclination. The fast precession (1) corresponds to the nutation of the force-free Euler gyro. This behavior, which neglects the force of gravity, is justified by the fact that with a fast top, the potential energy plays a subordinate role compared to the rotational energy .

The precession frequency corresponds to that of the pseudoregular precession of the fast Lagrange gyro . Due to secondary effects such as friction and deformation, the pseudoregular precession quickly changes into the regular one.

Nutation of the Euler gyro

For the Euler gyro , F _g s = 0 and the quadratic equation is reduced to

${\displaystyle [(C-A)u\mu +C\nu ]\mu =0}$

At μ = 0, the top only rotates around the figure axis or is completely at rest. The nutation of the Euler gyro takes place with (C - A) u μ = -C ν as a function of u = cos (wie) as in case (1) with the fast gyro.

Spherical pendulum

Fig. 6: Top as an upright spherical pendulum

The top without rotation (ν = 0) corresponds to a spherical pendulum whose regular precession consists in the fact that the pendulum body revolves on a circular cone . Here is the quadratic equation

${\displaystyle (C-A)u\mu ^{2}=F_{g}s}$

With a small axial moment of inertia (C <A), precession is only possible in the hanging position (with u = cos (ϑ) <0). The other case with axial inertia C> A is remarkable, where the spherical pendulum, as in Fig. 6, can only perform a regular precession with a center of mass above the point of contact (with u> 0).

Perennial rotations of symmetrical tops

Fig. 7: Carousel movement of a Kovalevskaya roundabout

→ Main article : Perennial rotation

If the center of mass is not on the figure axis, the symmetrical top can then perform a regular precession if the center of mass is still in the precession plane. This is the case with the carousel movements of the Kovalevskaya roundabout as in Fig. 7. The top rotates uniformly around a vertical axis that is fixed in space and the body, which is referred to as the Staude rotation .

stability

The stability of the precession movements depends on many factors. In general, it can be said that with the Lagrange top, the regular precession is always stable. The stability of the toy top depends on the angular momentum, the geometry of the lower tip of the top and the ratio of the main moments of inertia A and C. The stability of the nutation of the symmetrical Euler gyro and the Staude rotations is not easy to characterize and look up in the articles.

Regular precession of asymmetrical tops

Forced regular precession of asymmetrical tops

An asymmetrical, otherwise force-free top, like the symmetrical top, can be forced to perform any regular precession by appropriate torques. The case where the rotational axis fixed to the body is a main axis, for example the 3-axis, is of particular interest. For the sake of simplicity, the names of the symmetrical case are to be adopted here: The z-axis represents the precession axis, the 3-axis is called the figure axis and the rotation around it is called the self-rotation. The two axes span the precession plane to which the nodal axis is perpendicular. Then

${\displaystyle {\begin{aligned}{\vec {\omega }}=&\mu {\hat {e}}_{z}+\nu {\hat {e}}_{3}\\{\dot {\vec {\omega }}}=&{\dot {\nu }}{\hat {e}}_{3}+\nu {\dot {\hat {e}}}_{3}={\dot {\nu }}{\hat {e}}_{3}+\nu {\vec {\omega }}\times {\hat {e}}_{3}\\=&\mu \nu \sin(\vartheta )\cos(\varphi ){\hat {e}}_{1}-\mu \nu \sin(\vartheta )\sin(\varphi ){\hat {e}}_{2}+{\dot {\nu }}{\hat {e}}_{3}\end{aligned}}}$

given where a variability of the intrinsic rotation ν was allowed. Here it was used that the 3-axis ê ₃ , which is fixed to the body, has no time derivative relative to the top . Inserting these angular velocities and accelerations into Euler's gyroscopic equations yields the gyroscopic effect

${\displaystyle {\begin{aligned}{\vec {K}}=&-K_{a}{\hat {e}}_{N}-K_{b}{\hat {e}}_{N}\cos(2\varphi )+(K_{c}{\hat {e}}_{3}-K_{b}{\hat {e}}_{q})\sin(2\varphi )-C{\dot {\nu }}{\hat {e}}_{3}\\K_{a}=&\left[C\nu +\left(C-{\frac {A+B}{2}}\right)\mu \cos(\vartheta )\right]\mu \sin(\vartheta )\\K_{b}=&{\frac {A-B}{2}}[\mu \cos(\vartheta )+2\nu ]\mu \sin(\vartheta )\\K_{c}=&{\frac {A-B}{2}}\mu ^{2}\sin ^{2}(\vartheta )\end{aligned}}}$

The vectors

${\displaystyle {\hat {e}}_{N}:={\frac {{\hat {e}}_{z}\times {\hat {e}}_{3}}{\sin(\vartheta )}}}$ and  ${\displaystyle {\hat {e}}_{q}:={\hat {e}}_{3}\times {\hat {e}}_{N}}$

form an orthonormal basis with the 3-axis .

With constant ν , the gyroscopic action revolves around an ellipse with twice the intrinsic speed of rotation 2 ν , the plane of which contains the nodal axis ê _N , and the center of this ellipse is shifted along this axis by - K _a . In the case of the fast top with constant ν ≫ μ , K _c can be neglected compared to the other top effects K _{a, b} , after which the top action in the equatorial plane rotates circularly with radius K _b by - K _a ê _N. ${\displaystyle :={\dot {\varphi }}}$

If no intrinsic rotation is specified, i.e. ν is variable, then the oscillation equation results in the 3-direction ${\displaystyle K_{c}\sin(2\varphi )-C{\dot {\nu }}=0}$

${\displaystyle {\ddot {\alpha }}+{\frac {g}{l}}\sin(\alpha )=0}$

with   and   , where B> A can be assumed without restriction and g is the acceleration due to gravity . ${\displaystyle \alpha =2\varphi ,\;{\ddot {\alpha }}=2{\dot {\nu }}}$ ${\displaystyle l={\tfrac {Cg}{(B-A)\mu ^{2}\sin ^{2}(\vartheta )}}}$

"The asymmetrical top swings around the drive-free figure axis like a mathematical pendulum of length l , but always with half the deflection and half the speed, but with the same oscillation period."

- R. Grammel : Der Kreisel (1920), p. 80.

If the intrinsic rotation is initially large enough, then the oscillations turn into complete rotations, corresponding to a pendulum overturning. The fastest self-rotation occurs at sin ( α ) = 0 when the 1-axis with the smaller moment of inertia A passes the nodal axis, and it is slowest when sin ( α ) = ± 1 and the 2-axis with the larger moment of inertia B does that.

When self-rotation is suppressed ( ν  = 0), the top is forced to rotate around any axis fixed to the body. Suppose C> B> A . Then the gyroscopic action in the direction of the node is negative for an acute angle of inclination ϑ and positive for an obtuse angle. In any case, the gyroscopic effect tries to pull the figure axis, i.e. the axis with the greatest moment of inertia, into the axis of rotation.

Perennial rotations of asymmetrical tops

→ Main article : Perennial rotation

The Staude rotations are regular precessions possible for all gyroscopes in the form of permanent rotations around a vertical and body-fixed precession axis. The axis of gravity from the point of contact to the center of mass, the angular velocity and the angular momentum lie with constant components in the precession plane, which rotates evenly with the top around the precession axis, which lies on the Staude cone of the top . In Fig. 7 the Staude rotation of a symmetrical top can be seen.

Griolic precession

Fig. 8: Grioli's precession

→ Main article : Griolic precession

The Grioliʹsche precession is the only, dynamically possible, regular precession of heavy asymmetrical tops . With them the precession axis is not vertical, see Fig. 8. The components of the angular momentum in the precession plane are not constant and the angular momentum mostly does not lie in it either, but happens periodically. The Grioliʹsche precession can perform gyroscopes in which a circular section plane of their ellipsoid of inertia is perpendicular to the axis of gravity from the point of contact to the center of mass.

Web links

Commons : Precession  - collection of images, videos, and audio files

• K. Lüders, RO Pohl, G. Beuermann, K. Samwer: Precession of a rotating wheel. ( MP4 ) Institute for Scientific Film (IWF) , 2003, accessed on April 13, 2018 (Film about a regularly precessing wheel with a horizontal axis of rotation.). 
• K. Lüders, RO Pohl, G. Beuermann, K. Samwer: Rotation around free axes. ( MP4 ) Institute for Scientific Film (IWF) , 2004, accessed on February 5, 2020 (The free axes around which they can rotate in a stable manner are shown with three bodies of different shapes. The most stable free axis turns out to be the one with the greatest moment of inertia. ). 

Individual evidence

1. ↑ In Grioli (1947) characteristic properties of regular precessions are formulated and their dynamic realizability is shown. The Grioliʹsche precession also consider Leimanis (1965), p. 108 ff. And Magnus (1971), p. 143. See literature.
2. ↑ ^{a b c} Grammel (1950), p. 171 ff.
3. ^ Regular precessions are discussed in Grammel (1920), SV. 40, 89, 112, Grammel (1950), pp. 51, 69, 79, Magnus (1971), pp. 77, 117, Leimanis (1965), pp. 108 ff. And Klein and Sommerfeld (2010), pp. 279 ff. See literature.
4. ↑ Grammel (1920), p. 293 ff.
5. ↑ Grammel (1920), p. 67.
6. ↑ Grammel (1920), p. 66 ff.
7. ↑ Rauch-Wojciechowski, Sköldstam and Glad (2005), p. 340.
8. ↑ Rauch-Wojciechowski, Sköldstam and Glad (2005), p. 342.
9. ↑ Grammel (1920), p. 68 f.
10. ↑ Grammel (1920), p. 90, Magnus (1971), p. 118 ff.
11. ↑ Magnus (1971), p. 118.
12. ↑ ^{a b} Grammel (1920), p. 91.
13. ↑ Klein and Sommerfeld (2010), p. 292.
14. ↑ Grammel (1920), p. 106, Klein and Sommerfeld (2010), p. 289f.
15. ↑ Rauch-Wojciechowski, Sköldstam and Glad (2005), p. 357 ff.
16. ↑ Grammel (1920), p. 76 ff.
17. ↑ Grammel (1920), p. 81. See also the film "Rotation around free axes" at the #Weblinks .

literature

• K. Magnus : Kreisel: Theory and Applications . Springer, 1971, ISBN 978-3-642-52163-8 , pp. 77, 117 ( limited preview in Google Book Search [accessed February 20, 2018]).
• R. Grammel : The top . Its theory and its applications. Vieweg Verlag, Braunschweig 1920, DNB  451641280 , p. 40, 89, 112 ( archive.org - "swing" means angular momentum, " rotational shock " about the torque and "rotational force" rotational energy, see S. VII.).
• R. Grammel : The top . Its theory and its applications. 2. revised Edition volume 1 . Springer, Berlin, Göttingen, Heidelberg 1950, pp. 51, 69, 79 .
• Giuseppe Grioli : Existence and determination of dynamically possible regular precessions of a heavy asymmetrical body . In: Annali di Matematica Pura ed Applicata . tape 26 , no. 1 . Swets & Zeitlinger , 1947, ISSN  0373-3114 , p. 271–281 , doi : 10.1007 / BF02415381 (Italian, original title: Esistenza e determinazione delle precessioni regolari dinamicamente possibili per un solido pesante asimmetrico .).
• S. Rauch-Wojciechowski, M. Sköldstam, T. Glad: Mathematical analysis of the standing gyro . In: Regular and Chaotic Dynamics . tape 10 , no. 4 . Springer Nature, 2005, ISSN  1468-4845 , p. 333–362 , doi : 10.1070 / RD2005v010n04ABEH000319 ( turpion.org [accessed December 15, 2018] Original title: Mathematical analysis of the tippe top .).
• Eugene Leimanis: The general problem of the movement of coupled rigid bodies around a fixed point . Springer Verlag, Berlin, Heidelberg 1965, ISBN 978-3-642-88414-6 , p. 108 ff ., doi : 10.1007 / 978-3-642-88412-2 (English, limited preview in the Google book search [accessed on March 21, 2018] Original title: The General Problem of the Motion of Coupled Rigid Bodies about a Fixed Point .).
• F. Klein , A. Sommerfeld : The Theory of the Top . Development of the Theory in the Case of the Heavy Symmetric Top. Volume II. Birkhäuser, Boston 2010, ISBN 978-0-8176-4824-4 , pp. 279 ff ., doi : 10.1007 / 978-0-8176-4827-5 (English, symbols are explained on p. 197 ff., in particular p. 200). or the German original from 1897 F. Klein , A. Sommerfeld : About the theory of the gyro . Book I-III. Teubner, Leipzig 1897 ( archive.org [accessed January 17, 2020]).