Griolic precession

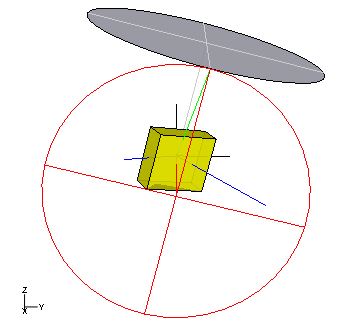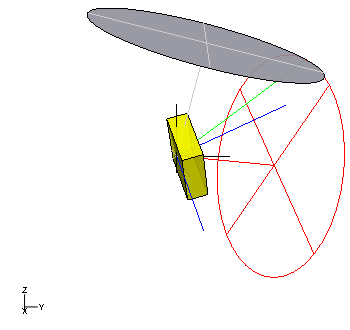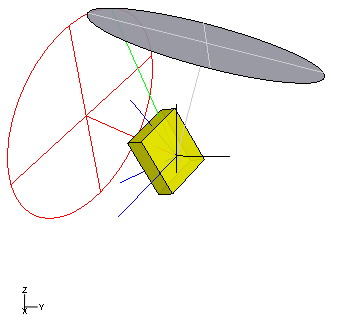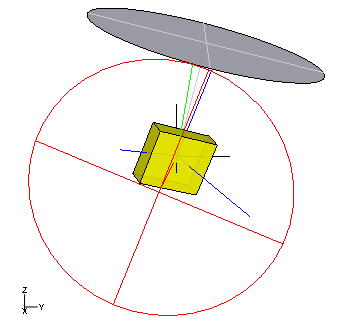
Grioli precession of a cuboid (yellow) with main axes (blue), center of gravity axis and gear pole cone (red), precession axis and detent pole cone (gray) and angular velocity (green). In the case of a block with the dimensions of a cigarette packet, one revolution takes about ½ second

The Grioli precession (after Giuseppe Grioli ) is the regular precession of an asymmetrical , heavy top in gyro theory .

The equations of motion can be integrated in a closed manner, making this motion one of the few known spatial solutions of the Euler-Poisson equations . Grioli showed in 1947 that regular precessions of the asymmetrical top are dynamically possible. MP Guljaev carried out the integration of the equations and proved that the precession found is the only possible one of the asymmetrical top.

Movement of the top

description

In the regular precession of the heavy symmetrical Lagrange top , the angle between the precession axis and the center of gravity axis , which leads from the base of the top to the center of gravity , as well as the angular velocity and the precession velocity remain constant over time. These characteristics are transferred here to the heavy asymmetrical top .

The precession axis is not perpendicular in the asymmetrical top. The center of gravity of the top revolves evenly in a fixed plane, perpendicular to the precession axis, which contains the support point and periodically passes the horizontal. The main axis with the medium-sized main moment of inertia is perpendicular to the center of gravity axis , it revolves around the precession axis at the same speed as the center of gravity and always passes through it when the center of gravity is horizontal.

The angular velocity is the bisector between the precession axis and the center of gravity axis and has a constant amount. Similar to the symmetrical Euler gyroscope , the angular velocity forms a fixed cone around the precession axis and in the body-fixed system a cone around the center of gravity. The two cones have an opening angle of 45 ° and roll off one another without sliding. The conversion of the positional energy into rotational energy and vice versa takes place here exclusively through rotation around axes with differently large moments of inertia .

The angle of inclination of the precession axis, the angular velocity and the total energy of the top are fixed for a given mass distribution in the top. The plane perpendicular to the axis of the center of gravity intersects the ellipsoid of inertia of the top in a circle, which places conditions on the mass distribution in the top.

The movement can be fully expressed using the sine and cosine .

Initial conditions

A gyroscope with the required mass distribution can be set into regular precession as follows . The center of gravity axis must be perpendicular to the precession axis, which includes the required angle with the vertical. The angular velocity with a given amount halves the angle between the precession and centroid axes. The main axes must be aligned in such a way that the required total energy of the gyro results and the angle between the center of gravity axis and the horizontal, which is perpendicular to the precession axis, and the angle between the main axis with the mean main moment of inertia and the precession axis coincide.

Analytical formulation

In the main axis system with 1, 2 or 3 axes and associated main moments of inertia A, B, C, the center of gravity _coordinates s _1,2,3 must _meet the condition

${\displaystyle s_{2}=0\,\quad {\text{und}}\quad {\frac {s_{3}^{2}}{s_{1}^{2}}}={\frac {B-C}{A-B}}}$

adhere to. Here was wlog A> B> C accepted. The space-fixed standard basis ê _{x, y, z} is aligned in such a way that the precession axis â has no x-component:

${\displaystyle {\hat {a}}={\begin{pmatrix}0\\\sin(\delta )\\\cos(\delta )\end{pmatrix}}_{{\hat {e}}_{x,y,z}}={\frac {1}{s}}{\begin{pmatrix}s_{3}\sin(\lambda )\\s\cos(\lambda )\\-s_{1}\sin(\lambda )\end{pmatrix}}_{{\hat {e}}_{1,2,3}}}$

with the angle of inclination

${\displaystyle \tan(\delta )={\frac {\sqrt {(A-B)(B-C)}}{A-B+C}}}$

the precession axis with respect to the vertical ê _z and the angle of rotation λ of the gyro around the precession axis . The center of gravity axis with the amount s runs according to

${\displaystyle {\vec {s}}=s{\hat {s}}=s{\begin{pmatrix}\cos(\lambda )\\\cos(\delta )\sin(\lambda )\\-\sin(\delta )\sin(\lambda )\end{pmatrix}}_{{\hat {e}}_{x,y,z}}={\begin{pmatrix}s_{1}\\0\\s_{3}\end{pmatrix}}_{{\hat {e}}_{1,2,3}}}$

around the precession axis. The main axes result in

${\displaystyle {\begin{array}{lclcl}{\hat {e}}_{1}\!\!\!\!&=&\!\!\!\!{\frac {1}{s}}{\begin{pmatrix}s_{1}\cos(\lambda )-s_{3}\cos(\lambda )\sin(\lambda )\\s_{1}\cos(\delta )\sin(\lambda )+s_{3}[\sin(\delta )\sin(\lambda )+\cos(\delta )\cos ^{2}(\lambda )]\\-s_{1}\sin(\delta )\sin(\lambda )+s_{3}[\cos(\delta )\sin(\lambda )-\sin(\delta )\cos ^{2}(\lambda )]\end{pmatrix}}_{{\hat {e}}_{x,y,z}}\!\!\!\!&=&\!\!\!\!{\begin{pmatrix}1\\0\\0\end{pmatrix}}_{{\hat {e}}_{1,2,3}}\\{\hat {e}}_{2}\!\!\!\!&=&{\begin{pmatrix}\sin ^{2}(\lambda )\\\cos(\lambda )[\sin(\delta )-\cos(\delta )\sin(\lambda )]\\\cos(\lambda )[\cos(\delta )+\sin(\delta )\sin(\lambda )]\end{pmatrix}}_{{\hat {e}}_{x,y,z}}\!\!\!\!&=&\!\!\!\!{\begin{pmatrix}0\\1\\0\end{pmatrix}}_{{\hat {e}}_{1,2,3}}\\{\hat {e}}_{3}\!\!\!\!&=&\!\!\!\!{\frac {1}{s}}{\begin{pmatrix}s_{3}\cos(\lambda )+s_{1}\cos(\lambda )\sin(\lambda )\\s_{3}\cos(\delta )\sin(\lambda )-s_{1}[\sin(\delta )\sin(\lambda )+\cos(\delta )\cos ^{2}(\lambda )]\\-s_{3}\sin(\delta )\sin(\lambda )-s_{1}[\cos(\delta )\sin(\lambda )-\sin(\delta )\cos ^{2}(\lambda )]\end{pmatrix}}_{{\hat {e}}_{x,y,z}}\!\!\!\!&=&\!\!\!\!{\begin{pmatrix}0\\0\\1\end{pmatrix}}_{{\hat {e}}_{1,2,3}}\end{array}}}$

with the angular velocity

${\displaystyle {\vec {\omega }}=\omega _{s}{\begin{pmatrix}\cos(\lambda )\\\sin(\delta )+\cos(\delta )\sin(\lambda )\\\cos(\delta )-\sin(\delta )\sin(\lambda )\end{pmatrix}}_{{\hat {e}}_{x,y,z}}={\frac {\omega _{s}}{s}}{\begin{pmatrix}s_{1}+s_{3}\sin(\lambda )\\s\cos(\lambda )\\s_{3}-s_{1}\sin(\lambda )\end{pmatrix}}_{{\hat {e}}_{1,2,3}}}$

The parameter

${\displaystyle \omega _{s}={\frac {\sqrt {2}}{2}}|{\vec {\omega }}|={\sqrt[{4}]{\frac {(mgs)^{2}}{(A-B)(B-C)+(A-B+C)^{2}}}}}$

is constant and equal to the angular velocity around the precession axis and the center of gravity axis.

It mean

• m the mass ,
• g is the acceleration due to gravity ,
• λ = ω _s t - ε the angle of rotation,
• t the time and
• ε any constant phase angle .

With λ = nπ, n = 0,1,2,… because of ê ₂ = (−1) ⁿ â the 2-axis lies on the precession axis. At the same time, because of ŝ = (−1) ⁿ ê _x, the center of gravity axis passes the x axis.

Derivation

The calculations use the principal axes system with 1-, 2- and 3-axis with base unit vectors ê _1,2,3 .

requirements

The center of gravity axis from the support point to the center of gravity is perpendicular to a circular section of the ellipsoid of inertia :

${\displaystyle s_{1}^{2}(B-C)=s_{3}^{2}(A-B),\quad s_{2}=0}$

see. the Hessian pendulum , where the sectional figure with the MacCullagh ellipsoid is circular. From the identities

${\displaystyle {\frac {A-B}{s_{1}^{2}}}={\frac {B-C}{s_{3}^{2}}}={\frac {A-C}{s^{2}}}=:k}$

is often used.

Angular velocities

As with regular precession , the amount of angular velocity and its projection onto the center of gravity is constant: ${\displaystyle {\vec {\omega }}=p{\hat {e}}_{1}+q{\hat {e}}_{2}+r{\hat {e}}_{3}}$

${\displaystyle {\begin{array}{lcccccl}\omega ^{2}&=&{\vec {\omega }}\cdot {\vec {\omega }}&=&p^{2}+q^{2}+r^{2}&=&{\text{const.}}\\\omega _{s}&:=&{\dfrac {{\vec {\omega }}\cdot {\vec {s}}}{s}}&=&{\dfrac {s_{1}}{s}}p+{\dfrac {s_{3}}{s}}r&=&{\text{const.}}\end{array}}}$

From the two equations, r can be eliminated and a functional relationship

${\displaystyle q(p)={\frac {1}{s_{3}}}{\sqrt {-s^{2}p^{2}+2ss_{1}\omega _{s}p+s_{3}^{2}\omega ^{2}-s^{2}\omega _{s}^{2}}}}$

be derived. The Euler's gyroscopic equations are:

${\displaystyle {\begin{aligned}A{\dot {p}}&=(B-C)qr-G_{2}s_{3}\\B{\dot {q}}&=(C-A)rp-G_{3}s_{1}+G_{1}s_{3}\\C{\dot {r}}&=(A-B)pq+G_{2}s_{1}\end{aligned}}}$

Therein are G _1,2,3 , the components of gravitational force . Multiplying the first gyro equation by s ₁ , the third by s ₃ and adding the resulting equations provides the condition

${\displaystyle s_{1}A{\dot {p}}+s_{3}C{\dot {r}}=(s_{1}p+s_{3}r)ks_{1}s_{3}q=s\omega _{s}ks_{1}s_{3}q}$

The time derivative of the constant ω _s gives another equation for calculating the angular accelerations with the result: ${\displaystyle s_{1}{\dot {p}}+s_{3}{\dot {r}}=0}$

${\displaystyle {\dot {p}}={\frac {s_{3}}{s}}\omega _{s}q\quad {\text{und}}\quad {\dot {r}}=-{\frac {s_{1}}{s}}\omega _{s}q}$

Substituting q (p) above gives an autonomous differential equation

${\displaystyle {\dot {p}}={\frac {\omega _{s}}{s}}{\sqrt {-s^{2}p^{2}+2ss_{1}\omega _{s}p+s_{3}^{2}\omega ^{2}-s^{2}\omega _{s}^{2}}}}$

which can be solved and with q (p) provide the angular velocities we are looking for:

${\displaystyle {\begin{aligned}p&={\frac {s_{1}}{s}}\omega _{s}+{\frac {s_{3}}{s}}\omega _{\bot }\sin(\omega _{s}t-\varepsilon )\\q&=\omega _{\bot }\cos(\omega _{s}t-\varepsilon )\\r&={\frac {s_{3}}{s}}\omega _{s}-{\frac {s_{1}}{s}}\omega _{\bot }\sin(\omega _{s}t-\varepsilon )\end{aligned}}}$

Here , t is the time and ε is a constant of integration . For the sake of clarity, the abbreviation λ = ω _s t - ε is used below . ${\displaystyle \textstyle \omega _{\bot }={\sqrt {\omega ^{2}-\omega _{s}^{2}}}}$

Weight force

With the first gyro equation

${\displaystyle {\dot {p}}={\frac {B-C}{A}}qr-{\frac {s_{3}}{A}}G_{2}={\frac {s_{3}}{s}}\omega _{s}q}$

the second component of the weight force can now be calculated:

${\displaystyle G_{2}={\frac {\omega _{\bot }}{s^{3}}}[\omega _{\bot }(C-A)s_{1}s_{3}\sin(\lambda )\cos(\lambda )-\omega _{s}(As_{1}^{2}+Cs_{3}^{2})\cos(\lambda )]}$

It also satisfies the third gyro equation. The second gyroscopic equation and the constant total energy E provide two conditions

${\displaystyle {\begin{aligned}B{\dot {q}}&=(C-A)rp-s_{1}G_{3}+s_{3}G_{1}\\E&={\frac {1}{2}}(Ap^{2}+Bq^{2}+Cr^{2})-s1G_{1}-s_{3}G_{3}\end{aligned}}}$

for determining the weight forces in 1 and 3 directions:

${\displaystyle {\begin{aligned}G_{1}&={\frac {1}{s^{2}}}\left\{s_{1}(E_{\text{rot}}-E)-s_{3}\left[B{\frac {\omega _{s}}{s}}(s_{3}p-s_{1}r)-(A-C)pr\right]\right\}\\G_{3}&={\frac {1}{s^{2}}}\left\{s_{3}(E_{\text{rot}}-E)+s_{1}\left[B{\frac {\omega _{s}}{s}}(s_{3}p-s_{1}r)-(A-C)pr\right]\right\}\end{aligned}}}$

Therein is the rotational energy . The weight is constant, so its time derivative disappears: ${\displaystyle E_{\text{rot}}={\tfrac {1}{2}}(Ap^{2}+Bq^{2}+Cr^{2})}$ ${\displaystyle \textstyle {\vec {G}}=\sum _{i=1}^{3}G_{i}{\hat {e}}_{i}}$

${\displaystyle {\dot {\vec {G}}}=\sum _{i=1}^{3}{\dot {G}}_{i}{\hat {e}}_{i}+\sum _{i=1}^{3}G_{i}{\dot {\hat {e}}}_{i}{\stackrel {\displaystyle !}{=}}{\vec {0}}}$

The time derivatives of the basis vectors are calculated according to the angular velocity , which is the consequence ${\displaystyle {\dot {\hat {e}}}_{i}={\vec {\omega }}\times {\hat {e}}_{i}}$

${\displaystyle \sum _{i=1}^{3}{\dot {G}}_{i}{\hat {e}}_{i}+\sum _{i=1}^{3}G_{i}{\vec {\omega }}\times {\hat {e}}_{i}={\vec {0}}\quad {\text{oder}}\quad {\begin{pmatrix}{\dot {G}}_{1}\\{\dot {G}}_{2}\\{\dot {G}}_{3}\end{pmatrix}}_{{\hat {e}}_{1,2,3}}={\begin{pmatrix}rG_{2}-qG_{3}\\pG_{3}-rG_{1}\\qG_{1}-pG_{2}\end{pmatrix}}_{{\hat {e}}_{1,2,3}}}$

Has. Inserting the above components G _1,2,3 shows that ω _⊥ = ω _s and thus ω = √2 ω _s . In addition, there is only one possible value for the total energy.

Energies

The energies of the top surrender to

${\displaystyle {\begin{aligned}E&={\frac {A+C}{2}}\omega _{s}^{2}=E_{\text{rot}}+E_{\text{pot}}\\E_{\text{rot}}&=\omega _{s}^{2}\left[{\frac {A+C}{2}}+(A-C){\frac {s_{1}s_{3}}{s^{2}}}\sin(\lambda )\right]\\E_{\text{pot}}&=-\omega _{s}^{2}(A-C){\frac {s_{1}s_{3}}{s^{2}}}\sin(\lambda )\end{aligned}}}$

The location of energy oscillates about the zero point at the level of the support point and the rotational energy in opposite directions around the constant mean value E .

Precession speed

The equations still have two free parameters ω _s and ε , the latter of which is arbitrary. Let λ = 0. Then the weight in the principal axis system is

${\displaystyle {\vec {G}}(\lambda =0)={\frac {\omega _{s}^{2}}{s^{3}}}[(B-C)s_{1}s{\hat {e}}_{1}-(As_{1}^{2}+Cs_{3}^{2}){\hat {e}}_{2}-(A-B)s_{3}s{\hat {e}}_{3}]}$

It has the amount mg with the mass m and the gravitational acceleration g , which is the angular velocity

${\displaystyle \omega _{s}={\sqrt[{4}]{\frac {(mgs)^{2}}{(A-B)(B-C)+(A-B+C)^{2}}}}}$

around the center of gravity axis and the precession axis.

Precession axis

In a regular precession , the axis of rotation rotates around a fixed axis, the precession axis â . Their time derivative must disappear, so that analogous to the weight above for the components a _1,2,3

${\displaystyle {\begin{pmatrix}{\dot {a}}_{1}\\{\dot {a}}_{2}\\{\dot {a}}_{3}\end{pmatrix}}_{{\hat {e}}_{1,2,3}}={\begin{pmatrix}ra_{2}-qa_{3}\\pa_{3}-ra_{1}\\qa_{1}-pa_{2}\end{pmatrix}}_{{\hat {e}}_{1,2,3}}}$

must apply. The axis

${\displaystyle {\hat {a}}={\begin{pmatrix}{\frac {s_{3}}{s}}\sin(\lambda )\\\cos(\lambda )\\-{\frac {s_{1}}{s}}\sin(\lambda )\end{pmatrix}}_{{\hat {e}}_{1,2,3}}}$

satisfies this condition with λ = ω _s t - ε . From the scalar product with the perpendicular weight

${\displaystyle {\frac {{\hat {a}}\cdot (-{\vec {G}})}{mg}}=\cos(\delta )={\sqrt {\frac {(A-B+C)^{2}}{(A-B)(B-C)+(A-B+C)^{2}}}}}$

the angle of inclination δ of the precession axis is determined in relation to the vertical. Because of

${\displaystyle {\hat {a}}\cdot {\vec {s}}=0\quad {\text{und}}\quad {\frac {{\hat {a}}\cdot {\vec {\omega }}}{\omega }}={\frac {{\vec {s}}\cdot {\vec {\omega }}}{s\omega }}=\cos 45^{\circ }}$

the angular velocity halves the right angle between the precession and the center of gravity axis at any time . The scalar products show that the rotational speeds around the precession axis and around the center of gravity are both equal to the parameter ω _s . ${\displaystyle {\hat {a}}\cdot {\vec {\omega }}={\frac {1}{s}}{\vec {s}}\cdot {\vec {\omega }}=\omega _{s}}$

Main axes

The axis of the center of gravity performs a circular movement around the precession axis â and periodically passes the x-axis. The spatially fixed base system { ê _x , ê _b = â × ê _x , â } is used for the representation

ŝ = cos ( λ ) ê _x + sin ( λ ) ê _b

of the centroid axis, where ŝ is the unit vector in its direction. The body circles around these, which can be described with the basis vectors { ŝ, ĥ = â × ŝ, â }. The basis vectors

î = sin ( λ ) â + cos ( λ ) ĥ

ĵ = cos ( λ ) â - sin ( λ ) ĥ

rotate as required by ge . The second main axis is perpendicular to the center of gravity axis and lies at λ = 0 on the precession axis , which implies ê ₂ = ĵ . The other two main axes result from

s ŝ = s ₁ ê ₁ + s ₃ ê ₃

s ê ₂ × ŝ = s î = s ₃ ê ₁ - s ₁ ê ₃

in the form specified in the section #Analytical formulation .

Symmetrical tops

The derivation and the formulas are also valid for the heavy symmetric top with A = B. Then s ₁ = s ₂ = 0 and s ₃ = s , so that the focus is on the symmetry or figure axis . The precession axis â is perpendicular because of tan ( δ ) = 0 and the center of gravity and figure axes perpendicular to it are horizontal. The angular velocity sweeps over because of

${\displaystyle {\vec {\omega }}=\omega _{s}{\begin{pmatrix}\cos(\lambda )\\\sin(\lambda )\\1\end{pmatrix}}_{{\hat {e}}_{x,y,z}}=\omega _{s}{\begin{pmatrix}\sin(\lambda )\\\cos(\lambda )\\1\end{pmatrix}}_{{\hat {e}}_{1,2,3}}\quad {\text{mit}}\quad \omega _{s}={\frac {\sqrt {2}}{2}}|{\vec {\omega }}|={\sqrt {\frac {mgs}{C}}}}$

a cone with an opening angle of 45 ° around the z-axis as well as around the figure axis. This special case is therefore the regular precession of a Lagrange top with a horizontal figure axis with the same speed of precession and speed of rotation around the 3-axis. With the angular momentum

${\displaystyle {\vec {L}}=\omega _{s}{\begin{pmatrix}C\cos(\lambda )\\C\sin(\lambda )\\A\end{pmatrix}}_{{\hat {e}}_{x,y,z}}=\omega _{s}{\begin{pmatrix}A\sin(\lambda )\\A\cos(\lambda )\\C\end{pmatrix}}_{{\hat {e}}_{1,2,3}}}$

becomes the condition

L _z * L ₃ = Amgs

fulfilled for the regular precession with a horizontal figure axis.

At B = C there is an analog movement with the 1-axis as the figure axis.

The case of Harlamova

EI Harlamowa constructed a solution to the gyroscopic equations that represents the only dynamically possible precession of an asymmetrical top around a vertical axis. The precession speed is not constant there and the main moments of inertia must meet the condition C> 2A> 2B . Therefore, the solution does not describe a rigid body , for with the is A + B> C . MP Guljaev noted that a rigid body with cavities filled with an incompressible ideal liquid can maintain the condition.

Remarks:

1. ↑ Leimanis (1965), p. 116.

literature

1. ↑ Giuseppe Grioli : Existence and determination of regular, dynamically possible precession movements of an asymmetrical heavy body . In: Annali di Matematica Pura ed Applicata . tape 26 , no. 1 . Swets & Zeitlinger , 1947, ISSN  0373-3114 , p. 271–281 , doi : 10.1007 / BF02415381 (Italian, original title: Esistenza e determinazione delle precessioni regolari dinamicamente possibili per un solido pesante asimmetrico .).
2. ↑ ^{a b} Eugene Leimanis: The General Problem of the Motion of Coupled Rigid Bodies about a Fixed Point . Springer Verlag, Berlin, Heidelberg 1965, ISBN 978-3-642-88414-6 , p. 109 ff ., doi : 10.1007 / 978-3-642-88412-2 (English, limited preview in Google Book Search [accessed on March 21, 2018]).
3. ↑ ^{a b} K. Magnus : Kreisel: Theory and Applications . Springer, 1971, ISBN 978-3-642-52163-8 , pp. 143 ( limited preview in Google Book Search [accessed February 20, 2018]).