Scientific work of Leonhard Euler
The scientific work of Leonhard Euler is the most comprehensive ever created by a mathematician. It includes basic results in the areas of calculus , analysis , mechanics , astronomy , geodesy , number theory , algebra , trigonometry , geometry , music theory and optics .
Euler's most famous results include the solution to the Basel problem , the polyhedron substitute, and Euler's identity , the latter drawing a close connection between numerous fundamental mathematical constants . For these and other results, Euler received many posthumous honors.

Euler's research was very diverse. He worked in almost all areas of mathematics and is considered one of the most productive mathematicians in history. His collected works of the Opera omnia so far comprise 76 volumes. There are a total of 866 publications by him. Euler's name is associated with a large number of results and scientific subjects.
Two mathematical constants are named after Leonhard Euler : Euler's number from analysis (see exponential function ) and the Euler-Mascheroni constant γ (gamma) from number theory, which is sometimes referred to as Euler's constant and is approximately equal to 0.57721 . It is not known whether γ is rational or irrational . In contrast to this, the irrationality of the number e is known and was first shown by Euler (see also: Proof of the irrationality of Euler's number ).
His popular scientific work Lettres à une princesse d'Allemagne from 1768, in which he wrote letters to Princess Friederike Charlotte von Brandenburg-Schwedt , a niece of Frederick II , the basics of physics, astronomy, the Taught mathematics, philosophy and theology.
Leonhard Euler's work had a lasting influence on many generations of mathematicians. Carl Friedrich Gauß said : "The study of Euler's works remains the best school in the various fields of mathematics and cannot be replaced by anything else". Because of the large number of publications and correspondence with other mathematicians and personalities, efforts to publish a complete work of Eulers continue to this day. However, with the publication of the Opera Omnia by the Euler Commission , this undertaking is largely implemented.
Mathematical notations
Euler introduced several notation conventions in his numerous textbooks. Due to the widespread use of the books, many of his notations became firmly established. He introduced the concept of the mathematical function and was the first to write f (x) to denote the function f that is applied to the argument x . The "formal" term used by Euler was an important milestone towards today's definition:
“If variables are interdependent in such a way that none of them can experience a change without at the same time causing a change in the other, then the one whose change is viewed as the effect of the change in the other is called a function of this , a term that extends so far that it includes all ways in which one quantity can be determined by another. "
The notations for the trigonometric functions , the letter e for the base of the natural logarithm , the Greek letter Σ ( sigma ) for sums and the letter i for the designation of the imaginary unit come from him . the symbol Δ ( delta ) for the difference is also from Euler. The use of the Greek letter π to denote the ratio of circumference and diameter ( circle number ) was also popularized by Euler, although it originally goes back to the Welsh mathematician William Jones .
Analysis and function theory
Elementary analysis
Euler can be seen as one of the founders of analysis . The math historian Thomas Sonar describes in his book 3000 Years of Analysis (2011) Leonhard Euler as a “real giant for analysis”. Euler's importance for this field is not only emphasized through the introduction of a rigorous functional concept. He is an “unbeaten master” in dealing with power series , which he understood as an “infinite polynomial ” and made his permanent “workhorse”.
Euler pioneered the use of analytical methods to solve problems in number theory. He thus united two dissimilar branches of mathematics and introduced a new field of study, analytical number theory .
calculus
Because of continued research, calculus was on the rise in the 18th century. Euler's friends, the Bernoullis, in particular, were responsible for much of the early advances in this area. Thanks to their influence, the study of calculus became the main focus of Euler's work. In his work Institutiones calculi differentialis (1755) he dealt systematically with differential calculus . Euler chose the interpretation: “Smaller than any specifiable quantity” for infinitesimal quantities. In the Institutiones calculi differentialis from 1755, Euler defines:
“There is no doubt that any size can be reduced until it disappears and becomes nothing. But an infinitely small size is nothing more than a vanishing size and so it is really 0. "
Euler regards calculating with infinitely small quantities as "calculating zeros". For these he introduced an "infinitely small" size and an "infinitely large" size (not to be confused with the imaginary unit) - and used these to derive correct statements. So Euler used with the approach for "any number initially valid"
around the series valid for Euler's number
derive. This formula gives an extremely rapidly convergent series for the number , for example it holds
Against the background of Euler's formula for it should be mentioned that for the limit value
what is valid is what classifies its -notation in the modern language of a mathematical limit .
Taylor series
Euler is known in this context for the development and frequent use of power series . These can be understood as "infinitely long polynomials " from which a function can be "globally reconstructed" in some cases from its local behavior (i.e. knowing all its derivatives and a point). Among other things, he gave direct evidence for Taylor series of the exponential function
and the arctangent function . Indirect proofs come from Newton and Leibniz from the period 1665 to 1680. Euler also developed the sine and cosine functions in their Taylor series around the development point 0:
He used this to derive Euler's formula for the exponential function by simply inserting it .
Infinite rows
In 1736 he found the long sought limit value for the infinite sum of the reciprocal square numbers (also by using power series) :
If you add up “all” (infinitely many) reciprocal values of the square numbers, the result is the number . This means that for every little number (about ) a square number exists such that for all the following squares applies
Since he had used previously unknown manipulation techniques for power series for this result , his original proof was not accepted. However, in 1743 Euler published another proof. From a generalization of this so-called Basel problem , he derived a closed representation for the even Bernoulli numbers . He showed, for example, that the sum of the reciprocal values of all fourth powers and sixth powers also strive against rational multiples of the corresponding powers of .
and in general
This has long been considered the best method for calculating Bernoulli numbers .
He used the identity
with the arctangent to derive a rapidly converging series for . Infinite rows like for example
or
with the Riemann zeta function also go back to Euler. It was Euler who was the first to systematically examine divergent series .
Trigonometric functions
Euler is the first author who relates the trigonometric functions to a circle with radius 1 and thereby normalizes them. This happens in the sixth chapter of the Introductio . In particular, the Pythagorean Theorem then immediately follows
A number of basic trigonometric formulas were systematically derived from Euler. He used the addition theorems of the trigonometric functions and was the first to give a simple and clear proof of De Moivre's well-known formula . From today's point of view, this proof is also considered to be strict, if one disregards the fact that the complete induction was not formally completed. From these formulas, Euler obtained the development of the trigonometric functions in power series by using the same procedure as in the case of the exponential function.
The partial fraction decomposition of the cotangene was also the subject of Euler's research. He discussed this, among other things, in a letter to Christian Goldbach on June 30, 1742.
In the context of his studies on the functions of a complex variable , some of which were anticipated by d'Alembert, Euler arrived at the result by means of a non-real substitution already used by Johann Bernoulli
In this context it is worth mentioning that Euler found the product formula by applying the addition theorem several times to the functions
generated.
Exponential function and logarithm

Euler first used the exponential function and logarithms in analytical proofs and successfully defined them for complex numbers . This greatly expanded their scope of application. This is how he found the close relationship to the trigonometric functions. For every real number (in radians ), Euler's formula says that the complex exponential function is the equation
Fulfills. A special case of the above formula is called Euler's identity
known. Euler's formula leads to proofs of addition theorems and De Moivre 's formula . So on the one hand
The multiplicativity of the exponential function is also used with regard to the addition theorems. On the other hand, we have accordingly
Two complex numbers are equal if and only if the real and imaginary parts match - for example, the following applies .
Justification of the calculus of variations
Along with Lagrange, Euler is one of the founders of the calculus of variations . Tying up with various problems and ideas from Jakob and Johann Bernoulli, Euler formulated their main problems very early on and developed general methods for their solution. This happened in his Methodus inveniendi lineas curvas, published in 1744 . This special discipline (initially initiated by the Bernoulli brothers) was first conceived and systematized by Euler. It deals with extreme value problems of the most general kind . In contrast to differential calculus , in which local maxima or minima of functions are often determined, the variational calculus is characterized by problems in which one or more unknown functions have to be determined in such a way that a given integral that is dependent on these functions assumes extreme values.
The Euler-Lagrange equation used in calculus of variations is named after Euler .
The following assessment comes from Carl Gustav Jacobi:
“The most important thing about the Methodus inveniendi is a small appendix, in which it is shown how the curve that the body describes gives a minimum in certain mechanical problems; however, only a body is assumed that moves in one plane. The whole of analytical mechanics has arisen from this appendix alone. Because soon after his appearance Lagrange, after Archimedes perhaps the greatest mathematical genius, 20 years old, came up with his analytical mechanics ... By generalizing Euler's method, he came up with his strange formulas, where in a single line the solution of all problems of the analytical Mechanics is included. "
Integral calculus
In his work Institutiones calculi integralis (1768–1770), published in three volumes, Euler dealt with integral calculus . This contains the methods of indefinite integration in a modern form, exhaustively presented for those cases in which the integration leads to elementary functions. Many methods were first developed by Euler, and Euler's substitution , with the help of which certain irrational differentials can be rationalized, is still a concept today. He found a way to compute integrals with complex limits, thus anticipating important parts of the development of complex analysis .
It should be noted that a precursor named after Laplace Laplace transform Euler in his already 1,766 Institutiones calculi integralis had been studied. Laplace had first used it in the context of probability theory .
Fourier series
Euler also worked in the area of Fourier series . He directed the formula valid for values
out of line
at the point :
Although the series on the right does not converge anywhere, integration on both sides, after choosing the correct integration constants, yielded the Euler's series known today as the correct .
This is a typical example of the "generality of algebra" used by Euler. Although some of Euler's proofs are unacceptable by modern standards of mathematical rigor, his ideas, as just demonstrated, led to much progress.
Transcendent functions
As a pioneer in this new field, Euler created the theory of hypergeometric series , q-series and hyperbolic trigonometric functions .
Riemann zeta function
Also the functional equation of the Riemann zeta function , the Euler for the related function
in the shape
stated, as well as some of their values in negative places, were already known to Euler. This is not a classic equation , such as that which is only solved by value , but an identity, i.e. H. the equation is true no matter what is used. For example, is a (trivial) identity, and in the case of the zeta function, Euler established a connection between the values and that is valid for all . He suspected this after extensive numerical calculations based on what is now known as the correct representation
were based. The Riemann zeta function plays a very important role in number theory and the functional equation was used by Bernhard Riemann , who presented a rigorous proof for the first time, to build his theory on prime numbers .
Beta and gamma function
Already in 1729 Euler developed the formula valid for natural numbers with the help of the binomial theorem
From this he derived an integral representation for the faculty function :
These results led to the discovery of the beta and gamma functions by Euler, who studied their basic properties. In correspondence with Christian Goldbach in 1729, Euler first generalized the faculty and in 1730 introduced the Euler integral of the second type, which represents the Euler gamma function for complex values with a positive real part :
Already in a letter of 1729 to Christian Goldbach Euler had a formula for the half-integer faculty mentioned in the form: . The integral of the first kind represents the beta function for :
From the special properties of these functions, Euler not only derived relationships to the Euler-Mascheroni constant , but also gave the product formulas
and
the latter as Euler supplementary set (Euler reflection formula) is known. The beta function is the basis of the beta distribution from probability theory . The gamma function appears in the gamma distribution , but also plays an important role in function and number theory, among other things in the context of completed L-functions .
Elliptic integrals
Euler's great interest in elliptic integrals and elliptic functions goes back to his early years with Johann Bernoulli . While studying at the Berlin Academy, Euler received a two-volume work from Giulio Fagnano on December 23, 1751, entitled Produzioni Matematiche , which was published in 1750 for his formal review. This work contained the formula for doubling the arc length of the lemniscate , whose polar coordinate equation , and whose algebraic equation is. Euler was hugely inspired by this work and helped create a new area of algebraic functions .
Euler was able to prove the result known today as the addition theorem for elliptic integrals (first kind). If one sets with whole numbers , then it follows from equality
already
This is called Euler's addition theorem . In 1753 Euler discovered many addition formulas for elliptic integrals which are usually directly related to the addition theorem.
Number theory and combinatorics
Euler's interest in number theory can be traced back to the influence of Christian Goldbach , his friend at the St. Petersburg Academy. Number theory is basically the science of natural numbers and their properties. A number-theoretic property of a number is, for example, whether it can be divided by another number or by how many numbers it can be divided by. For example, Euler had the insight that a number is greater than just divisible by and itself (is a prime number ) if there is only one way to write it as the sum of two prime prime numbers greater than . For example, the number has a non-trivial divisor, so it is not a prime number, there
But in the case it holds that the numbers and are prime, and otherwise there is no further possibility of a decomposition into two non-trivial squares. So is a prime number. However, it should be noted that on the other hand, not every prime number can be written as the sum of two squares. Much of Euler's early work on number theory is based on the works of Pierre de Fermat . Euler developed some of Fermat's ideas and refuted some of his guesses.
Various numbers and sequences of numbers are named after Euler , see Euler's numbers (disambiguation) .
Elementary number theory
For example, he refuted Fermat's conjecture that all Fermat numbers are also prime numbers by showing that the number is divisible by 641.
He made a major contribution to the theory of perfect numbers , which had fascinated mathematicians since Euclid . Euler proved that the relationship between (even) perfect numbers and Mersenne primes shown by Euclid is even one to one , a result known as the Euclid-Euler theorem . In 1772 Euler had correctly stated in a letter to Goldbach that 2,147,483,647 is a Mersenne prime number. It was considered the largest prime number found until 1867. As early as 1732 he was able to get the 19-digit perfect number
to construct.
Algebraic Number Theory
He gave several proofs for Fermat's little theorem and was the first to publish a proof (the proof given by Leibniz in 1683 did not appear until 1894). His first proof was by induction , which was unusual for the time. He also introduced Euler's Phi function . Using the properties of this function, he generalized Fermat's little theorem into what is now known as Euler's theorem.
Euler did important preliminary work for Lagrange's four-squares theorem by proving in 1751 that every positive rational number can be written as the sum of four rational squares. Already earlier, in 1748, he had the identity in a letter to Goldberg
mentioned, which reduced the problem to prime numbers. After Lagrange showed that any positive whole number can be written as the sum of four whole squares, Euler soon provided a simpler proof. It applies, for example
Another idea of Euler's work, which emerged from his study of the Partitio numerorum , is to prove Lagrange's theorem. For this he looked at the power series
where for the four-squares theorem for all n is sufficient. Euler suggested this proof idea in letters to Goldbach and in some papers (such as E394, E586). So he wrote in August 1750: "This way seems to me to be the most natural way to get to the proof [...]". The considered power series is the fourth power of a modified theta series - Jacobi later went this way to prove Lagrange's theorem purely analytically.
He also showed Fermat's theorem about the sum of two squares . This provides a criterion for when a positive whole number can be written as the sum of two whole squares. For example, the following applies , but there is no possibility of such a decomposition for the number .
Euler showed Fermat's great theorem for cases and . He proved that no square number greater than zero can be written as the sum of two biquadrates greater than zero, which already implies that the equation has no positive integer solutions. In the case Euler factored to . By using this variant of the Gaussian numbers and an implicit assumption of unique factorization, Euler was able to construct a proof that showed the impossibility of the case . As with his proof of the case, Euler's proof was based primarily on manipulations of algebraic symbols and parity arguments and introduced little new method. Like generations of mathematicians after him, however, Euler failed on the general proof of Fermat's great theorem. A complete proof was only given in 1995 by Andrew Wiles and Richard Taylor as a consequence of the modularity theorem for semi-stable elliptic curves .
Euler suspected the law of quadratic reciprocity , which was later proven by Carl Friedrich Gauß . This is one of the most basic concepts in number theory.
Combinatorics
Although combinatorics later became a new modern branch of mathematics, problems of counting have a long and early history. Euler looked at problems of permutations and combinations and formulated a particular problem as follows: Given any sequence of letters , how many possibilities are there to rearrange it so that none of them revert to the original position? In this context, Euler introduced the notation to represent the number of permutations of the letters in which none of them resumes their original position. Such a permutation is known today as a fixed-point-free permutation .
With a simple argument, Euler proved several recursion formulas for , including the double recursion formula
He also gave the explicit formula
which proves that the quotient of fixed-point-free permutations and all permutations converges rapidly to the number .
The pentagonal number theorem is also based on Euler
back, he showed it in 1750. A recursion formula for the partitions can be derived from this. This was used by Percy Alexander MacMahon to calculate the values of the partition function up . The function that counts is how many ways can be written as the sum of natural numbers. For example is because . It applies . The pentagonal number theorem is also a cornerstone between combinatorics and the theory of modular forms .
Analytical number theory
Euler linked the nature of the prime number distribution with ideas from analysis. For example, he proved that the sum of the reciprocal values of the prime numbers diverges . In doing so he found the connection between the Riemann zeta function and the prime numbers; his discovery is known today as the Euler product formula for the Riemann zeta function:
where the product extends over all prime numbers . As it turned out later, this identity has far-reaching consequences for statements about the distribution of prime numbers. Euler's work in this area led to the development of the prime number theorem .
Continued fractions
Based on previous work of his predecessors Euler began his research on continued fractions and published in 1737 in a work entitled De Fractionibus Continuis many new ideas and results. He also proved that any rational number can be represented by a finite continued fraction and found an infinite continued fraction for the number in the following form:
From this (and from an equally infinite representation as a continued fraction for ) Euler deduced the irrationality of and . He gave non-regular continued fractions (without only ones in the numerators of the new fractions) for the circle number , such as
He also proved a theorem that says that the solution of a quadratic equation is real if and only if it has a periodic continued fraction expansion.
The Euler-Mascheroni constant
Euler first discovered in 1734 (possibly earlier) a connection between the growth of natural logarithms and the harmonic sequence . Although the terms tend towards 0 for increasing values , the following applies
So the sum of the reciprocal values of all natural numbers is unbounded. However, if one subtracts the term from the harmonic sequence , the unlimited growth is removed and the difference converges to a value which is now called the Euler-Mascheroni constant or Euler's constant :
Despite this fundamental definition, the algebraic properties from to this day are largely unexplained. It is believed to be irrational , however no evidence has yet been found. In 1736 he had already calculated the number in his work E47 to 15 digits.
Geometry, topology and graph theory
geometry
Euler made the majority of his discoveries in geometry through the use of algebraic and analytical methods. The teaching structure, both flat and spherical trigonometry, owes its current form - including the notation - to Leonhard Euler. His studies - initiated by Johann Bernoulli - on geodetic lines on a surface were trend-setting for the later development of differential geometry . Of even greater importance were his discoveries in area theory , from which Gaspard Monge and other researchers would subsequently proceed. In his later years, Euler finally resumed his work on the general theory of space curves exactly where Clairaut had left off in 1731 - although it was only printed posthumously.
In the fundamentals of differential geometry, he made contributions to the curvature of a curve and derived an analytical formula for the radii of the osculating circles. He also discovered the two main normal sections of a surface and the main curvatures and . One of his results, the so-called Euler equation, gives the curvature of any other normal section that forms an angle with one of the sections with the main curvature, in the form It was Euler who first dealt with developable surfaces (e.g. a cylinder or a cone ) employed, d. H. Surfaces that can be deformed into a plane without distortion such as stretching or tearing. A surface is called a ruled surface (e.g. a cylinder, cone, hyperboloid, or hyperbolic paraboloid ) if it can be created by moving a straight line in space.
It is known that Euler determined purely mathematically the circle involute, first studied by Jakob Bernoulli and Christiaan Huygens , as the most favorable profile shape for the flanks of gears. When used sensibly, this curve provides optimal mechanical properties with regard to friction loss, low noise levels and power transmission (this discovery or invention of Euler was not technically realized until the 19th century with the involute toothing ). What is less well known is that in this work E330, which was written as early as 1762, Euler anticipated the equation now named after Felix Savary . It is used to determine the radius of curvature of a rolling curve and enables an elegant construction of its centers of curvature.
Within the elementary geometry, Euler deals, among other things, with a forerunner of the double ratio and the "little moon" of Hippocrates . He dedicated two widely spaced works E73 and E423 to the latter. In a short treatise E648 from 1779, Euler solved the so-called tactical problem of Apollonius . This requires the (elementary always possible) construction of a (fourth) circle that touches three arbitrarily given circles in the plane. However, this problem was solved by François Viète , Isaac Newton and others before Euler . Shortly afterwards, in E733, he generalized the problem to three-dimensional space and found the construction of the contact sphere to be four arbitrarily given spheres. This construction, too, only leads to a quadratic equation and can therefore be carried out in an elementary way.
topology
In a letter dated November 14, 1750 from Berlin to Christian Goldbach in Saint Petersburg, Euler announced his discovery of a fundamental relationship between the important sizes of a convex polyhedron. His discovery was the formula for the number of vertices ( E ), edges ( K ) and surfaces ( F ) of a convex polyhedron , a planar graph. This theorem is known today as Euler's polyhedron theorem.
Probably the most prominent convex polyhedron is the cube : It has 8 corners, 12 edges and 6 faces,
8 - 12 + 6 = 2A dodecahedron has 20 vertices, 30 edges and 12 faces. The following applies:
20 - 30 + 12 = 2An icosahedron has 12 vertices, 30 edges and 20 faces. Similar to the left, 12 - 30 + 20 = 2 applies
Eight years after his letter, in 1758, he published two papers on the subject. The first contained his discovery, the second an attempt to prove it. Euler's proof, in which he wanted to break down the examined objects into individual tetrahedra , contained an error in severity by today's standards. This gap was highlighted in 1924 by Henri Lebesgue .
Euler hoped to be able to classify all polyhedra with his work, but did not achieve this goal. After the publication of the two works, he no longer turned to the topic.
The constant in Euler's set of polyhedra is now called the Euler characteristic of the graph (or another mathematical object) and is directly related to the mathematical gender of the object. The first complete proof of the polyhedron substitution came only from Adrien-Marie Legendre . The study and generalization of this formula, especially by Cauchy and L'Huilier , marks the beginning of ( algebraic ) topology .
Graph theory
In 1735 (published in 1741 with the work Solutio problematis ad geometriam situs pertinentis ) Euler presented a solution to the Königsberg bridge problem . The city of Königsberg in Prussia lay on the Pregel River and comprised two large islands that were connected to one another and to the mainland by seven bridges. The problem is deciding whether it is possible to choose a path that crosses each bridge exactly once and returns to the starting point. This is not possible because at least one piece of land has an odd number of bridges. This condition is already fulfilled by the bridges leading to the central island. The bridge problem is synonymous with the question of whether there is an Euler circle for the graph corresponding to the city map .
This solution is considered to be the first theorem of graph theory , especially planar graph theory .
Applied Mathematics
Numerics and differential equations
Euler-Maclaurin Formula
Euler discovered the formula in 1732
with the Bernoulli numbers and the remainder
Bernoulli denote polynomials . This was found independently by Colin Maclaurin and is now called the Euler-Maclaurin formula . The formula creates a connection between sums and the integral . The terms in the end contain the (higher) derivatives of at the boundary points and can usually be calculated quickly if the choice is skilful (usually not too high) . Euler and Maclaurin's empirical formula is useful when the sum is very difficult to calculate but the integral is easy to calculate. For example is
difficult to generally calculate while the bill
is much easier to perform (see also: Integral calculus and antiderivative ) - it should be noted that the sum formula is not set to any specific limits and can therefore also start with 1 instead of 0. Alternatively, if you start at a large starting value , then is approximately given by
On the other hand, the empirical formula can be used to approximate a (difficult to calculate) integral over discrete sums. Accordingly, Euler took advantage of this formula in practical terms to quickly numerically approximate infinite series that converge slowly. So he gave good approximations for the values and and found exactly to 20 digits:
If Euler had instead “naively” summed up the terms for such a precision , the time required with 20 seconds per summand would have been around 63 trillion years. It has been proven that Euler's original method of calculating for higher values established numerical mathematics as a new field of research.
Explicit Euler method
During the seventeenth and eighteenth centuries, mathematicians made serious attempts to solve ordinary differential equations in terms of elementary functions and quadratures. When these methods failed, they solved equations using infinite series and numerical methods. In 1768 Euler developed a simple finite difference method for the numerical solution of an ordinary differential equation
with the given initial condition . With a uniform step size between the points , Euler constructed the points with , and then received the formula
Here refers to the O notation of Landau and in this case means that the error noise beyond the right expression mainly due to the "tiny" number is not exceeded. If is continuous, then the sequence of Euler polygon lines converges uniformly with to the unknown function on a sufficiently small closed interval that contains.
Euler angle
The important Euler angles are named after him. It is a triple of angles with which the orientation (rotational position) of a solid body in three-dimensional Euclidean space can be described. An algebraic description with which the rotational position of any point could be calculated was only formulated by Euler in increasing depth from 1775. In the first work he showed that the nine elements of the mapping matrix (which describe the rotation) are not independent of each other due to the length accuracy of a movement, but are defined by only three mutually independent angles, the Euler angle.
In the aerodynamics of aircraft , the Euler angles are used to this day. It is common practice to use an earth-fixed coordinate system to describe the position and orientation of an aircraft relative to earth. Since the coordinate system is not a Cartesian system , there are usually some problems with the formulation of the aircraft dynamics. This can be countered by further differentiation. While the position of the aircraft can best be described by means of an earth-fixed coordinate system, the components of the inertia tensor in the equation of motion are best described by means of a coordinate system which has the center of gravity of the aircraft as its origin. The orientation of an aircraft relative to the earth can now be described using the so-called Euler angles. It is therefore necessary to derive the transformation between the two upper coordinate systems by means of the three Euler angle rotations.
Lotteries
Euler also dealt with lotteries . In 1749, an Italian businessman named Roccolini approached Frederick the Great, then King of Prussia, with the proposal to introduce a lottery system in which five numbers from 1 to 90 should be drawn. The king sent the proposal to his scientific advisor Euler with a request for a mathematical review regarding the introduction of a state lottery in Germany. At the royal request, Euler became very interested in analyzing the various aspects of the Genoese lottery system and developed an improved lottery system after addressing combinatorial issues in analyzing this game of chance. As a result, the Berlin Lottery was founded in Germany in 1763.
In the same year in which Prussia held its first lottery , Euler read a paper with a detailed and general analysis of this lottery in front of the Berlin Academy. Euler's work was published posthumously. One of the fundamental results that Euler achieved was to find a formula for the probability of winning the bet, in which r must be correctly guessed from t numbers drawn for a total of n . His formula was:
Using these probability calculations, Euler calculated three practical scenarios for the payouts on all bets, taking into account the possibility of generating a profit for the lottery organizers.
growth of population
In 1907, nearly 125 years after Euler's death, Alfred J. Lotka used Euler's work Recherches générales sur la mortalité et la multiplication du genre humain to derive the Euler-Lotka equation for calculating population growth rates. This is a fundamental method that is used in population biology and ecology to this day.
physics
mechanics
According to his "program", Euler's treatises on mechanics can be divided into the following areas: Fundamentals of mechanics (structure and structure of matter, force and measure of force, principles of mechanics), mechanics of material points, mechanics of rigid, mechanics of flexible non-elastic, mechanics elastic, mechanics of liquid and mechanics of gaseous bodies. In writings such as Mechanica, sive motus scientia analytica exposita (1736), Découverte d'un nouveau principe de mécanique (1752) and Theoria motus corporum solidorum seu rigidorum (1765), Euler applied mathematics to questions of physics. According to Clifford Truesdell, “in fact, few movements contribute as much to the mechanics” as the second mentioned work.
Rigid body mechanics
Euler noticed that the then generally accepted principles of mechanics were insufficient to solve the problem of the motion of a rigid body in full generality. The theorem of angular momentum (around an axis fixed in space) can already be found - implicitly formulated - in Euler's 1734 manuscript for his Mechanica and in his Scientia navalis , which was written in 1738 but only published in 1749 . The theorem of angular momentum (with respect to a fixed axis) for systems of discrete mass points was derived for the first time in a treatise by Euler on the motion of the lunar nodes, which Euler presented to the Berlin Academy of Sciences in 1744 and published in 1750. On September 3, 1750, he read a mémoire in front of the Berlin Academy, in which he presented the principle “force equals mass times acceleration” in the context of Euler's equation of rigid body rotation as a new discovery of his own. However, it was not until 1775 that Euler published the law of angular momentum in its most generally valid form as an independent new mechanical principle. From an idea by Johann Bernoulli in his work Hydraulica and from the application of a cutting principle to an infinitesimally small volume element, Euler obtained the momentum principle of mechanics ,
So the “ force = mass × acceleration ” so common today , which is always attributed to Newtons, but is not found there in this form.
Fluid mechanics

Historically, significant advances in theoretical fluid mechanics were made in the 18th century by Jean d'Alembert, Daniel Bernoulli, Alexis Clairaut, and Joseph Lagrange . Among these great mathematicians, Euler made the most fundamental contributions to fluid mechanics by establishing his famous equations of motion, the Euler equations of fluid mechanics .
Euler's main work in the field of fluid mechanics was essentially based on the continuum hypothesis and Newton's laws of motion . His work forms the basis of the mathematical theory of fluid mechanics, which was encompassed by his discovery of the calculus of variations and partial differential equations . He made fundamental contributions to hydrostatics and hydrodynamics in the period from 1752 to 1761 and in 1757 published several important articles in these areas in the Mémories de l'Academie des Sciences de Berlin . The first of these articles looked at the basic general concepts, principles, and equilibrium equations of liquids. The second and third theses dealt mainly with the conservation of mass equation (or the equation of continuity) and the nonlinear Euler equations of motion of compressible fluid flows. He then formulated the equations of motion and the equation of continuity for a non-viscous , incompressible fluid flow with the first proof of the famous d'Alembert's paradox in a non-viscous fluid flow that flows past a rigid body.
In addition, Leonhard Euler worked in mechanics in the fields of turbine equation and gyroscopic theory , in which he introduced the Euler angles in addition to Euler's equations . He is considered to be the developer of the world's first water turbine. A reconstruction of the Euler turbine showed that its efficiency of 71% is only slightly below that of modern turbines (as of 2015). The technically feasible principle of the impeller drive and the propeller is also thanks to Euler.
Technical mechanics
The first analytical description of the buckling of a bar loaded with a compressive force also goes back to Euler; he founded the stability theory . He helped develop the Euler-Bernoulli beam equation , which became a cornerstone of engineering.
astronomy
Aside from successfully applying his analytical tools to problems in classical mechanics, Euler also applied them to astronomy - this work was recognized throughout his career by a number of awards from the Paris Academy. His achievements include accurately determining the orbits of comets and other celestial bodies , understanding the nature of comets, and calculating solar parallax . His calculations contributed to the development of precise longitude tables .
According to Victor J. Katz , it is considered certain that Euler was the first mathematician in Europe who systematically penetrated the calculus of trigonometric functions. He did this in works that appeared from 1739 onwards. He became aware of the importance of trigonometric functions a few years later when he sought to solve certain differential equations , particularly linear differential equations with constant coefficients . The retrospectively obvious fact that calculating with trigonometric functions is a key to understanding “periodic phenomena”, including the motions of planets and satellites , does not seem to have been obvious to astronomers before Euler. Euler was the first to deal with the formulation and solution of the perturbation problem - the key problem that had to be formulated and solved if Newton's law of gravitation was to be established as the basis for the planetary and lunar theory .
With the calculation of the trigonometric functions in hand, he constructed a series of tables of the moon. These were published in his Opuscula varii argumenti in 1746 . Euler's first attempt to cope with the planetary perturbations came in response to the Paris Academy's prize competition in 1748. The prize was awarded for “a theory of Jupiter and Saturn that explains the inequalities that these planets cause in their movements cause seem particularly about the timing of their conjunction ”. Newton had written in his Principia of "a disturbance in the orbit of Saturn in every conjunction of this planet", "which is so sensitive that astronomers are at a loss". In response to the announcement of the Paris Academy's prize draw for 1748, Euler wrote two memoirs, both completed in mid-1747. In the first, which Euler presented to the Berlin Academy, he derived the differential equations for the problem of disturbances. The second, a derivative of Jupiter's perturbations of Saturn, was entered in the competition and won the award, although Euler failed to explain Saturn's apparent slowing down or Jupiter's speeding up. Euler's prize essay impressed with the innovative methods he introduced to cope with planetary disturbances.
optics
In optics , he published works on the wave theory of light and the calculation of optical lenses to avoid color errors . He contradicted Newton's corpuscle theory of light in the Opticks , which was prevalent at the time. His work on optics from the 1740s contributed to the wave theory of light proposed by Christiaan Huygens becoming the predominant way of thinking, at least until the development of the quantum theory of light.
Almost the majority of Euler's writings on optics, seven out of fifteen in all, are devoted to questions of dispersion . Among other things, he was repeatedly concerned with the question of whether red or purple has the higher frequency . Euler changed his view on this three times, each time on the basis of a theoretical consideration which a new experiment he had heard about had prompted him to do. In the nova theoria , red still had the greatest frequency, in two later works he corrected this view based on his theory of observations of colors in thin layers. But then, by considering the elasticity of metal lamellas, it is brought back to the first incorrect view, and then finally to the correct one.
ballistics
In 1745 Euler translated the work New principles of gunnery by the Englishman Benjamin Robins into German. It was published in Berlin in the same year under the title New principles of artillery containing the determination of the power of the powder along with an investigation into the difference ( sic ) of the resistance (sic) of the air in fast and slow movements. Since Galileo , the artillerymen had viewed the trajectories of the projectiles as parabolas, considering the air resistance to be negligible. Robins carried out one of the first experiments on ballistics and showed that the flight path is significantly influenced by air resistance. Thanks to Robins and Euler's help, "the first textbook on ballistics" was created. For example, it was introduced in France (in French translation) as an official textbook in military schools. Napoleon Bonaparte had to study it as a lieutenant.
shipbuilding
Less well-known are Euler's works on the stability criterion of ships, in which he renewed the knowledge that Archimedes had already acquired, but lost again . The Scientia navalis , the main work on marine engineering, which anticipated well into the 19th century, appeared during the first years of Berlin.
algebra

In algebra, Euler dealt among other things with the explicit form of roots of unity . These appear as solutions to the equations . In the 18th century it was considered a pioneering problem to express the solutions of these equations in an algebraic way using “radicals”. Euler was also successful in this area and solved the unit equations up to . Technically particularly difficult is the method for , which expresses the solutions in terms of square and cube roots .
Euler intensively studied Diophantine equations of the form and , where are integers and not a square number. In greater generality, he examined equations of the type
where the discriminant is not a square number.
Euler worked out approximate methods for solving numerical equations and also worked on the elimination problem - probably suggested by Daniel Bernoulli . He succeeded in proving Newton's already known theorem that two algebraic curves of degree m or n can have at most mn intersections . In this context he came to the important concept of the resultant . In the two papers E147 and E148 of the year 1750, Euler gave a sound explanation of the so-called Cramer's paradox .
In 1770 he brought out the book Complete Guide to Algebra . He developed a method for solving quartic equations . Euler also noticed that Quintic equations can generally no longer be solved by radicals ( i.e. closed chains of root expressions ). This result was only later proven by Niels Henrik Abel and Évariste Galois .
logic
Euler is also credited with using closed curves to illustrate syllogistic reasoning. These diagrams have come to be known as Euler diagrams. Letters 101 to 108 (to a German princess), written in February and March 1761, introduce the diagrams now known as Venn diagrams, although this is a misnomer. Diagrams for mathematical representations in logic appeared in some eighteenth-century treatises on the subject, and it is possible that Johann Heinrich Lambert used them shortly before Euler's letters. In Letters 101 and 102, Euler emphasized the need for disciplined language in the presentation of general ideas and their expansion; he used circles on diagrams to explain various forms of syllogisms and hypothetical propositions .
An Euler diagram is a diagrammatic means of showing sets and their relationships. Euler diagrams consist of simple closed curves (usually circles or ellipses ) in the plane, each of which represents quantities. Each Euler curve divides the plane into two areas or “zones”: the inner area, which symbolically includes and represents the elements of the set, and the outer area, which represents all elements that do not belong to the set ( complement ). The sizes or shapes of the curves are irrelevant. The diagram is only intended to illustrate how they overlap. The spatial relationships between the areas bounded by each curve (overlap, delimitation or neither) correspond to set-theoretical relationships ( intersection , subset and disjointness ). Curves whose inner zones do not intersect represent disjoint sets. Two curves whose inner zones intersect represent sets that have elements in common (non- empty intersection): The zone within both curves represents the set of elements, the two sets are common. A curve that is completely contained within the range of another represents a subset of them.
Euler diagrams (and the more general Venn diagrams ) were included in the course of New Mathematics as part of the teaching of set theory from the 1960s .
Cartography and Geodesy
Euler showed great interest in astronomical-geodetic and cartographic questions, for the solution of which a new scientific institution was set up at the Petersburg Academy of Sciences at the suggestion of Joseph-Nicolas Delisle - the so-called Geographical Department . Euler worked there as Delisle's helper for a number of years. A look at various documents of this department, especially the protocols, revealed many details about Euler's work in the field of geodesy and cartography . So could z. For example, it can be stated that Euler's position in the Department of Geography was entirely in keeping with his wishes and scientific inclinations. Euler's first work was the Senate-requested map of Russia's European borders. On September 2, Euler conferred with Delisle on how best to construct such a map. Euler finished the map of the European borders of Russia on September 6, 1736. It was not until October 14, 1736 that the map that Euler and Delisle had started together, after corrections by Adjunct Vasili Evdokimowitsch Adodurow , was finally completed.
Mathematical music theory
In the field of music, too, Euler's thoughts were mainly based on mathematics: He founded a music theory based on mathematical laws (including Tentamen novae theoriae musicae , 1739, Music mathématique, Paris 1865). His model of the sound network is still used today in calculations for pure tuning . Although his writings on music theory make up only a small part of his work (a few hundred pages for a total production of about thirty thousand pages), they nonetheless reflect an early interest that has not left him in his entire life.
To understand Euler's music theory, it must be known that musical intervals in the so-called pure tuning with the pitches octave, fifth , fourth and major third corresponding to the frequency ratios 1: 2, 2: 3, 3: 4 or 4: 5 to the fundamental being constructed. In contrast to this, there is nowadays the common tuning (well tempered), in which two tones of a semitone always have the exact frequency ratio .
First, Euler defines consonances, i.e. H. Harmonies, a "degree". This is intended to mathematically capture the "difficulty" of a harmony of tones. A low level speaks for an "acceptable" - a high level for an "unpleasant" sound. As a function, Euler used the degree suavitatis ("degree of loveliness, of compatibility") , which can be interpreted in a purely abstract way as a number-theoretic function : for a natural number n with prime factorization it is defined by
The gradus suavitatis thus represents an evaluation of the prime factorization of natural numbers and is larger, the larger the prime numbers and the larger their exponents. Two chords are now graded as follows: For the ratio a : b , where it was already completely shortened, i.e. i.e., a and b are coprime , one sets
Euler calls the number (the least common multiple of a and b ) the exponent of a : b . For example, the perfect fifth has a degree of 4, because it applies . This principle can be extended to any chords by using the LCM of the overall sound. For a triad a: b: c , where a , b and c are each prime, one has, for example . Euler's arguments explain, for example, why a major triad (like CEG, in the ratio 4: 5: 6) sounds “happier” than a minor triad (EGH, in the ratio 5: 6: 7). In his scheme, the major triad has the ninth degree, the minor triad the fourteenth degree - the minor triad is therefore “sadder” because “joy from things that have a simpler, more easily perceptible order, and sadness from those Things whose order is more complex and difficult to perceive ”is conveyed. So Euler used the principle of the exponent to propose a derivation of the gradus suavitatis of intervals and chords from their prime factors - one must bear in mind that initially he only used the intonation , i.e. H. the 1 and the prime numbers 3 and 5. The above-mentioned gradient function, which extends this system to any number of prime numbers, was proposed later.
Another approach of Euler's music theory is the definition of so-called "genres", i. H. of possible subdivisions of an octave by the prime numbers 3 and 5. These represent successive tones that follow certain frequency relationships and are therefore scales . Euler describes 18 such genera, based on the prime numbers 3 and 5. The procedure is as follows: Each product describes a sequence of multiples of a fundamental frequency - all possible divisors of are taken. For example, one has the ratios 1: 1, 1: 2, 1: 3, 1: 5, 1: 6, 1:10, 1:15, 1:30. However, since the number 2 (except for the octave) does not change anything in the sounds that occur (a frequency doubling defines an octave jump), the power of two does not matter for the genre.
Euler presented his genres in compact tables that visually juxtapose musical and mathematical notations. He showed how important both were to him and how he tried to bring them together:
This principle was further developed by Adriaan Fokker . For example, the case can be normalized within an octave to the following ratios: 1: 1, 8: 9, 16:21, 2: 3, 4: 7, 32:63.
The genres 12 (with Euler ), 13 (with Euler ) and 14 (with Euler ) are corrected versions of the diatonic , chromatic and enharmonic versions from ancient times. The 18th genus ( ) is the "diatonic-chromatic", "which is generally used in all compositions" and which proves to be identical to the system described by Johann Mattheson . Euler later saw the possibility of describing genera including the prime number 7. Euler developed a special diagram, the Speculum musicum , to illustrate the diatonic-chromatic genre, and explained the paths in this diagram for certain intervals, reminding of his interest in graph theory, in particular the Seven Bridges of Königsberg. The concept aroused renewed interest as a tonnet in the Neo-Riemannian theory (Neo-Riemannian Theory) , named after the music theorist Hugo Riemann .
Popular representations and themes
His popular scientific treatise Lettres à une princesse d'Allemagne from 1768, in which he wrote letters to Princess Friederike Charlotte von Brandenburg-Schwedt , a niece of Frederick II, learned the basics of physics and astronomy, achieved special significance among the general public , who taught mathematics, philosophy and theology. Euler began the first letter with an explanation of the term " size " (la grandeur) . Based on the definition of a foot , he defined the mile and motivated the different dimensions with practical examples. So it is better to put the distance between Berlin and Magdeburg at 18 miles (one translation speaks of 83 English miles ) instead of 432,000 feet (43.824 feet ). Later letters included optics, magnetism, electricity, but also astronomy. Among other things, Euler estimated the distance between the earth and the sun to be “trente Millions de Milles” (thirty million miles).
The first two volumes of the 234 letters originally written in French were published in Saint Petersburg in 1768 and the third in Frankfurt in 1774. The letters were later reprinted in Paris, the first volume in 1787, the second in 1788 and the third in 1789. The first edition of the Lettres , published in Paris in 1787, contained Eloge de M. Euler , a thirty-six page obituary written by the Marquis de Condorcet , who gave the reader a biographical Sketches and highlights of Euler's career. Although Euler wrote the letters in French, it is considered certain that Condorcet made some editorial changes, as the text differs from the original.
Euler also devoted himself to chess mathematics , for example the knight problem . This deals with the question of whether it is possible that the knight chess piece can pass each square of a chessboard exactly once during a round trip. Euler mentioned the problem in a letter to Christian Goldbach in 1757. In the years 1758–1759 he finally wrote a paper on the subject, which was published in 1766 in the Berlin Mémoires .
He is considered to be the inventor of the Greco-Latin square , a predecessor of Sudoku . This is (with order n ) a square n x n scheme, in whose fields elements of two ( n -element) sets are entered in such a way that exactly one copy of each element appears in each column and row. Examples are:
In his work, Recherches sur une nouvelle espece de quarres magiques , Euler gives hundreds of examples of such squares and also deals with squares whose diagonals fulfill the required property. In the end, he claims, but without providing rigorous evidence, that a Greco-Latin square of size 4 k + 2 cannot be constructed. It was not until 1960 that it was revealed that Euler was wrong. Greco-Latin squares always exist, with the exception of orders 2 and 6. For the algebraic-algorithmic construction, group theory , finite bodies , projective geometry and block plans were used.
Processing of the archived estate
Posthumous publication process
After Euler's death, the St. Petersburg Academy published previously unpublished works by Euler's in their Mémoires posthumously . Due to the large number of documents (around 100 articles), the publication process was only declared completed in 1830. But it soon turned out that Euler had written other papers. After Paul Heinrich von Fuss had become the secretary of the St. Petersburg Academy as the successor to his father in 1825, he researched its archives and found some parcels from the correspondence between Eulers and a. with the Bernoullis. From this grew a directory of the correspondence in two volumes under the title Correspondance mathématique et physique de quelques céleèbres géomètres du XVIIIème siècle . A list of Euler's writings was added to this. After Fuss 'father Nikolaus' directory did not yet contain 700 numbers, this has now been expanded to 756. For the further completion the archives were searched again and one produced a work not yet published under the title Astromania mechanica .
Publication of a complete work
First attempts in the 19th century
The first attempts to publish Euler's complete works go back to the 1830s. There were essentially two initiatives. One of them was brought into being by Paul Heinrich Fuss. Although Fuss was encouraged by many prominent mathematicians, including Carl Gustav Jacobi , the project was eventually abandoned when it turned out to be beyond the financial capabilities of the academy's budget. The only result of the initiative of Fuss and Jacobi was the publication of two volumes of Commentationes arithmeticae in 1849, which include 94 already published articles and five unpublished manuscripts. At the same time, a group of Belgian mathematicians undertook a similar project. They were more successful than Fuss and Jacobi in that five volumes of this edition were actually printed. This edition has been sharply criticized, in particular by the Belgian mathematician Henri Bosmans , who described it as a "very bad work". In order to make Euler's works accessible to a large part of the public, the editors had changed the original texts, some arbitrarily, even if the original was already written in French. Ease of access by other mathematicians is seen as the driving force behind the editors, and the work should still have a "stimulating effect" on them today.
Beginning of the 20th century
At the beginning of the 20th century, with the start of the bicentenary of Euler's birthday, the Russian Academy of Sciences launched a new initiative to publish Euler's complete works. Faced with the failure of previous attempts, the Russians sought allies with whom they could share work and costs; the institution that came to mind with regard to Euler was the Prussian Academy of Sciences in Berlin, which Euler had served for twenty-five years. The Berlin academics were initially quite enthusiastic about this plan. But when it turned out that the Russian Academy wanted to split up the task of publishing the mathematical and physical corpus and claim the former for itself, enthusiasm waned. The Prussian Academy asked the most respected physicist among its members, Max Planck , for an assessment of the proposal. In a famous statement, Planck said that it may be true that mathematicians are still inspired by Euler's writings, but that the same is not true of physicists. He suspected that the publication of Euler's physical writings was "not in the interest of physics as a science of our time" and therefore refused to allow the Prussian Academy to help finance the project. Since a complete edition was too expensive for the Russian Academy, this initiative also ended in failure.
Gustaf Eneströms Euler Directory
Between 1910 and 1913, the Swedish mathematician Gustaf Eneström created a directory listing all of Euler's works. This has 866 numbers, which are arranged according to the principle E001, ..., E866.
Foundation of the Euler Commission and the Opera omnia
After the failed attempts in the 19th century, Leonhard Euler's 200th birthday in April 1907 was the occasion for the Swiss Natural Research Society to start another complete edition of Euler's publications. The initiative came from the mathematician Ferdinand Rudio , who was a professor of mathematics at the Zurich Polytechnic (today's ETH Zurich ). In a fiery speech at the celebration of Euler's 200th birthday, which took place in Basel in the presence of numerous foreign scholars, Rudio skilfully appealed to Swiss patriotism and international solidarity: For Euler's home country "the publication of his works is an honorary duty", however Switzerland "needs the support of the two countries in which Euler achieved fame and glory", Germany and Russia:
“Switzerland will always retain the feeling of gratitude to the St. Petersburg and Berlin academies that they have given our Euler, for whom his own fatherland was too small, a bigger one and given him the opportunity to complete his great life's work with unadulterated creativity. "
Rudio's words met with strong resonance everywhere. The Swiss Natural Research Society set up an Euler Commission to run the company, and Rudio was elected president. The first action of the young commission was an appeal for donations. A promise of further financial support also came from the Petersburg Academy. The latter also offered to “make available all the materials in their archives that should be necessary for the best possible execution of the company”. From 1910 to 1912, the entire Euler estate reached Switzerland in seven boxes as diplomatic mail via the Russian embassy. Although the work (supported by eminent mathematicians such as Alexander Lyapunov ) initially proceeded quickly, the Euler Commission was affected by the political discord in Europe. There were considerable reservations in Switzerland against the communist system of the Soviet Union, and between 1918 and 1946 there was no diplomatic relationship between the two states. Nevertheless, the scientists continued to have a more difficult connection. While a request of May 28, 1921 for a delay because of "war-related problems" was still accepted by the Russian side, the Petersburg Academy in 1930 demanded the manuscripts back. The Euler Commission refused to comply with this request, which sparked a lively exchange of letters. The Swiss side tried initially with various arguments to repeatedly delay the return of the manuscripts. In July 1930 the Soviet Academy agreed that the manuscripts should remain in Zurich “for some time” and asked for a precise schedule for the edition of the outstanding volumes. After Andreas Speiser did not give in to the request from Russia to return at least those manuscripts that were no longer needed , the tone grew sharper. The Soviet Academy itself set a deadline on June 5, 1933:
“The Academy of Sciences of the USSR has the honor to inform you that The Committee on Scientific. and educational institutions at the Central Executive Committee in Moscow has recognized it as appropriate to keep Euler's manuscripts in Zurich for a period of two years from today's date. "
Although the Commission initially approved these requirements, it had to find out as early as the next year that the schedule could not be adhered to. In an unsuccessful appeal to Giuseppe Motta , the head of the Political Department of Switzerland, Speiser wrote that "this publication [...] should take at least twenty years". Due to further printing from Russia, the production of copies and also photographs began. This was completed in 1938. The final handover of the documents did not take place until May 15, 1947 in Zurich. The Euler Commission successfully contributed to the publication of the Opera Omnia .
Of the 81 planned volumes in four rows, 76 have now (as of 2018) appeared. Series I (mathematics: 29 volumes) and Series III (physics, varia: 12 volumes) are complete, of the 31 volumes of Series II (mechanics, astronomy) two are still outstanding (II / 26 and II / 27 on celestial mechanics), the content of which should be completed in the course of 2019 at the earliest. In Series IVA (correspondence) 8 of the 9 planned volumes have so far been published, including the two double volumes IVA / 3 and IVA / 4. The vernissage of the latest volume IVA / 8 was on November 23, 2018. The last volume IVA / 9 is being edited by a group of historians under the direction of Antonio Moretto.
Further publications from 1950 to 1980 in the Soviet Union
When the Euler estate returned to Russia in the archives of the Leningrad Academy, Soviet scientists were given new opportunities for extensive research and vigorously took advantage of this opportunity. In 1958, Gleb K. Michailow (born 1929) and Vladimir Ivanovich Smirnov (1887–1974) reported for the first time on these activities. In addition, in 1962 and 1965, a very detailed, but uncommented list of the Euler material stored in the Academy's archive was published in two volumes. The first volume contains a list of 2,268 letters from and to Euler (without annotations) that are kept in the Petersburg archive. Since the 1950s, the Soviet Academy and now also the Russian Academy of Sciences devoted particular attention to the indexing and processing of Leonhard Euler's correspondence, which was not included in the original plans of the Opera omnia Euleri . In cooperation with the German Academy of Sciences in Berlin, the general correspondence appeared in three volumes and the correspondence between Euler and Christian Goldbach was published. In 1963 a volume was published with selected scientific letters that Euler wrote to 19 (young) scientists (all letters were translated into Russian). A list of Euler's letters was published in Russian by Adolf Pavlovič Jušskevič (1906-1993) and Vladimir Ivanovič Smirnov, which contained all known letters in Russia and outside Russia. The list contains a total of 2,654 letters from and to Euler and a short summary.
In the 1970s, the collaboration between the Euler Commission in Zurich and the Soviet Academy was intensified through the expansion of the Euler edition. The correspondence and the scientific notes are collected in a new fourth series of the Opera omnia Euleri . The first volume of this series appeared in 1975 and contained a revised list of 2,892 letters from the correspondence.
In the digital age
A large number of Euler's primary sources are freely available as a result of digitization on the Internet . In contrast, Euler's Opera omnia is not for free use, but digital images of the original versions of over 95 percent of his published works, which were scanned from the original pages of the 18th century, can be called up in the so-called Euler archive . The then students Lee Stemkoski and Dominic Klyve are considered the founders of this website . The online documents lack the corrections and introductions from the editors of the Opera omnia , but they are accessible to anyone with an internet connection, and the editors of the Euler Archives are gradually adding links to comments and translations. It is estimated that by 2033 (Euler's 250th year of death) the relative roles of print and digital editions will be better assessed.
reception
His mathematical work inspired many generations of mathematicians. Among other things, he influenced the work of Pierre-Simon Laplace , Joseph-Louis Lagrange , Carl Friedrich Gauß , Carl Gustav Jacobi , Niels Henrik Abel , Évariste Galois , Karl Weierstraß and Bernhard Riemann .
Mathematical historians emphasize the importance of Euler's work up to the present day. Dirk Struik sees Euler's “Fertility” as a “source of surprise and admiration”. With regard to Euler's work, in his Outline of the History of Mathematics in 1967, he notes that studying it “would not be as difficult as it seems”, because Euler's Latin is “very simple” and its terms “almost resemble today's”. Euler's method consisted of proceeding from the simplest examples to more general contexts, which made the presentation broader than the abstract style in use today; accordingly, deficiencies in mathematical rigor were also criticized.
Fonts
Leonhard Euler is considered one of the most productive mathematicians in history. His collected works of the Opera omnia so far comprise 76 volumes. There are a total of 866 publications by him. His oeuvre thus comprises an estimated one third of the entire body of mathematical, physical and mechanical research within the last three quarters of the 18th century.
Publications (selection)
- Mechanica sive motus scientia analytice exposita. 2 volumes, 1736 ( E015 , E016 ).
- Tentamen novae theoriae musicae . 1739 ( E033 ).
- Introduction to the art of arithmetic for the use of the Gymnasii at the Imperial Academy of Sciences in St. Petersburg. 2 volumes, Academische Buchdruckerey, Saint Petersburg; Volume 1 1738, Volume 2 1740. ( Digitized version and full text in the German Text Archive Volume 1, digitized version and full text in the German Text Archive Volume 2).
- Solutio problematis ad geometriam situs pertinentis. 1741 ( E053 ).
- Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu accepti. 1744 ( E065 ).
- Introductio in analysin infinitorum. 2 volumes, 1748 ( E101 , E102 ).
- Découverte d'un nouveau principe de Mécanique. In: Mémoires de l'académie des sciences de Berlin. Volume 6, 1752, pp. 185-217 ( E177 ).
- Institutiones calculi differentialis. 2 volumes, 1755 ( E212 ).
- Theoria motus corporum solidorum seu rigidorum. 1765 ( E289 ).
- Lettres à une princesse d'Allemagne. 3 volumes, 1768 ( E343 , E344 , E417 ).
- Institutiones calculi integralis. 3 volumes, 1768–1770 ( E342 , E366 , E385 ).
- Complete guide to algebra. 2 volumes, 1770 ( E387 , E388 , volume 2 digitized and full text in the German text archive ).
German translations and editions of his works
- Leonhard Euler's complete guide to integral calculus. Ed. Joseph Solomon, 3 volumes, Vienna 1828 to 1830, Volume 1, ETH Library , Volume 1, Archives , Volume 2, Archives , Volume 3, Archives.
- Leonhard Euler's mechanics or analytical representation of science. 3 volumes, published by J. Ph. Wolfers, Greifswald 1848 to 1853, Volume 1, Archives , Volume 2, Archives , Volume 3, Archives.
- Euler, Johann Bernoulli, Jacob Bernoulli: Treatises on calculus of variations. 1st part, Ostwalds Klassiker 46, Leipzig 1894, archive.
- Euler: Two treatises on spherical trigonometry. Ostwalds Klassiker 73, Leipzig 1896, archive.
- Euler: Three treatises on map projection. Ostwalds Klassiker 93, Leipzig 1898, archive.
- Jakob Bernoulli, Leonhard Euler: Treatises on the equilibrium and the oscillations of the flat elastic curves. Ostwald's classic 175, Leipzig 1910.
- Euler: More complete theory of the machines that are set in motion by the reaction of water (1754). Ostwald's classic 182, Leipzig 1911.
- Euler: Three treatises on solving equations (1783, 1764, 1790). Ostwald's classic 226, Leipzig 1928.
- Euler: Introduction to the Analysis of the Infinite. Part 1, introduction by Wolfgang Walter, Springer, 1983.
- Euler: On the theory of complex functions. Introduction by AP Juschkewitsch, Ostwalds Klassiker 261, Akademische Verlagsgesellschaft, 1983.
Opera Omnia
Euler published around two dozen books and 500 scientific articles. The German mathematician Ferdinand Rudio (1856–1929) initiated the publication of all of Euler's works. More than 30 volumes were published during Rudio's lifetime. Over 70 individual volumes had been published by 2013, as well as four volumes from the extensive correspondence. The works appear in the original language, mostly French or Latin.
The collected works have been published as Opera Omnia by Birkhäuser (Springer) Verlag since 1911 by the Euler Commission , which was founded by Ferdinand Rudio. At that time Adolf Krazer , Rudolf Fueter , Heinrich Weber , Paul Stäckel and Karl von der Mühll were also involved in the publication. The later editors of individual volumes included Ludwig Schlesinger , Friedrich Engel , Andreas Speiser , Clifford Truesdell (physics, mechanics, the whole volume 11-1 is a history of elasticity theory in the 17th and 18th centuries, written by Truesdell), Alexander Mikhailovich Lyapunow , Georg Faber , August Gutzmer , Carl Boehm , Constantin Carathéodory , Henri Dulac , Max Herzberger , Emile Cherbuliez , Charles Blanc and Eric Aiton (physics). After Rudio, the main editors were Andreas Speiser (from 1928), Walter Habicht (from 1965) and, since 1985, Hans-Christoph Im Hof . Other editors included Emil Fellmann , Adolf Juschkewitsch , Henri Dulac, Pierre Costabel , René Taton , Wladimir Iwanowitsch Smirnow , Alot T. Grigorjan, Joachim Otto Fleckenstein , Johann Jakob Burckhardt , Gleb K. Mikhailov, Franz Lemmermeyer , Andreas Kleinert and Martin Mattmüller .
The edition consists of
- Row 1: Mathematics, 30 volumes (complete). The first volume in 1911 was the manual for algebra. Volume 16 consists of two volumes.
- Series 2: Mechanics and Astronomy, 27 volumes in 30 partial volumes (complete).
- Row 3: Physics and Others, 12 volumes (complete).
- Row 4a: Correspondence. Planned: 9 volumes for around 3100 letters with around 300 correspondents. Published so far: 8 volumes.
- Row 4b: notebooks, diaries and unpublished items (planned).
Letters
During the correspondence of the Opera Omnia appeared:
- Volume 1 (summary of contents, overview, 1975),
- Volume 2 (with Johann I. and Nikolaus I. Bernoulli),
- Volume 5 (with Clairaut , d'Alembert and Lagrange ) and
- Volume 6 (with Maupertuis and Friedrich II.).
In addition, the following correspondence has appeared outside the Opera Omnia :
- with Goldbach (Akademie Verlag, Berlin 1965),
- with the Berlin and Petersburg academies (Akademie Verlag, Berlin, 3 volumes: 1959, 1961, 1976),
- with Tobias Mayer (American Elsevier, 1971).
In 1845 Paul-Heinrich Fuss published parts of Euler's correspondence with Goldbach, Nikolaus Fuss , Johann I, Nikolaus and Daniel Bernoulli. Volume 14 of Lagrange's edition also includes the correspondence with Euler.
Individual evidence
- ^ William Dunham: Euler: The Master of Us All. Mathematical Association of America, 1999, ISBN 978-0-88385-328-3 . P. 17.
- ^ H. Heuser: Textbook of Analysis II. P. 686.
- ^ Carl B. Boyer, Uta C. Merzbach: A History of Mathematics. John Wiley & Sons, 1991, ISBN 978-0-471-54397-8 . Pp. 439-445.
- ^ Rüdiger Thiele: Leonhard Euler. Leipzig 1982, p. 115.
- ^ Jones, William: Synopsis Palmariorum Matheseos. P. 243, accessed February 24, 2020.
- ^ Thomas Sonar: 3000 Years of Analysis. Springer, pp. 455-456.
- ^ Thomas Sonar: 3000 Years of Analysis. Springer, p. 462.
- ^ Thomas Sonar: 3000 Years of Analysis. Springer, p. 463.
- ^ Isaac Newton: De analysi per aequationes numero terminorum infinitas. July 31, 1669, written in Latin, in section [15] De serie progressionum continuanda.
- ^ Raymond Ayoub: Euler and the zeta function . In: Amer. Math. Monthly . 81, 1974, pp. 1067-86. doi : 10.2307 / 2319041 . P. 1079.
- ^ Leonhard Euler: Demonstration de la somme de cette suite etc. orig. published in Journ. lit. d'Allemange, de Suisse et du Nord, 2: 1, 1743, pp. 115–127.
- ↑ David Harvey: A multimodular algorithm for computung Bernoulli numbers. October 2008, (arXiv) .
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 202.
- ^ Steven R. Finch: Mathematical Constants. Encyclopedia of Mathematics and its Applications 94, Cambridge University Bridge, 2003, p. 20 and p. 44.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 223.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 202.
- ^ Thomas Sonar: 3000 Years of Analysis. P. 465.
- ↑ Aleksander O. Gelfond: About some characteristic features in L. Euler's ideas in the field of mathematical analysis and his introduction to the analysis of infinity. In: Leonhard Euler 1707 - 1783: Contributions to life and work. P. 106.
- ^ Leonhard Euler: Correspondence. Opera omnia, Series Quarta A, Vol, 1, p. 142.
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work. In: Leonhard Euler 1707 - 1783: Contributions to life and work. Pp. 46-47.
- ^ Carl B. Boyer, Uta C. Merzbach: A History of Mathematics. John Wiley & Sons, 1991, ISBN 978-0-471-54397-8 , pp. 439-45.
- ^ Emil A. Fellmann: Leonhard Euler 1707 - 1783: Contributions to life and work. P. 51.
- ^ Emil A. Fellmann: Leonhard Euler 1707 - 1783: Contributions to life and work. P. 52.
- ^ Thomas Sonar: 3000 Years of Analysis. P. 456.
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work In: Leonhard Euler 1707 - 1783: Contributions to life and work. P. 47.
- ↑ L. Euler: Institutiones Calculi Integralis , Volume Secundum (1769), ed. By F. Engel and L. Schlesinger, Opera Omnia, Ser. 1, vol. 12, Teubner, Leipzig and Berlin, 1914, pp. 242-243
- ↑ P.-S. Laplace: Des Fonctions génératrices , Théorie analytique des Probabilités , (2nd ed.), Paris, 1814, Chapter I. Sections 2–20.
- ^ Teun Koetsier: Lakatos' philosophy of mathematics: A historical approach. North-Holland, 1991, pp. 206-210.
- ^ Gerhard Wanner, Ernst Hairer: Analysis by its history. Springer, 2005, p. 63.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 216.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. Pp. 235-236.
- ^ Leonhard Euler: Correspondence. Opera omnia, Series Quarta A, Vol, 1, p. 134.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 236.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 240.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 242.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 184.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. Pp. 188-189.
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work. In: Leonhard Euler 1707 - 1783: Contributions to life and work , p. 36
- ^ William Dunham: Euler. The master of us all. Volume 22, pp. 4-5.
- ^ Chris Caldwell: The largest known prime by year. Retrieved January 26, 2020.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 62.
- ^ Jeff Suzuki: Euler and Number Theory: A Study in Mathematical Invention. In: Leonhard Euler: Life, Work and Legacy. Pp. 371-372.
- ^ John Stillwell: Mathematics and Its History. 3rd edition, Springer, p. 423.
- ^ Jeff Suzuki: Euler and Number Theory: A Study in Mathematical Invention. In: Leonhard Euler: Life, Work and Legacy , p. 375.
- ^ Herbert Pieper: The Euler of the 19th century: CG Jacob Jacobi. Elem. Math. 60 (2005), 89-107, p. 104.
- ^ Jeff Suzuki: Euler and Number Theory: A Study in Mathematical Invention. In: Leonhard Euler: Life, Work and Legacy , pp. 381–382.
- ^ Gary Cornell, Joseph H. Silverman, Glenn Stevens: Modular Forms and Fermat's Last Theorem , Springer, p. 10
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 98.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. Pp. 343-344.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 71.
- ^ Wright Hardy: An introduction to the theory of numbers. Clarendon Press 1975, p. 286.
- ^ William Dunham: Euler: The Master of Us All. Mathematical Association of America, 1999, ISBN 978-0-88385-328-3 . Chapters 3 and 4.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 80.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 80.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 81.
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work. In: Leonhard Euler 1707 - 1783: Contributions to life and work , p. 93.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. Xvii.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 178.
- ^ Steven R. Finch: Mathematical Constants. Encyclopedia of Mathematics and its Applications 94, Cambridge University Bridge, 2003, p. 30.
- ↑ Ronald S. Calinger: Leonhard Euler: Mathematical Genius in the Enlightenment. Princeton University Press, 2016, p. 107.
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work. In: Leonhard Euler 1707 - 1783: Contributions to life and work , pp. 52–53.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 137.
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work. In: Leonhard Euler 1707 - 1783: Contributions to life and work , pp. 53–54.
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work. In: Leonhard Euler 1707 - 1783: Contributions to life and work. P.56.
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work. In: Leonhard Euler 1707 - 1783: Contributions to life and work. P. 58.
- ↑ David Richeson: The Polyhedral Formula. In: Leonhard Euler: Life, Work and Legacy. P. 421.
- ↑ David Richeson: The Polyhedral Formula. In: Leonhard Euler: Life, Work and Legacy. P. 421.
- ↑ David Richeson: The Polyhedral Formula. In: Leonhard Euler: Life, Work and Legacy. P. 425.
- ↑ David Richeson: The Polyhedral Formula. In: Leonhard Euler: Life, Work and Legacy. P. 421.
- ^ Alan Gibbons: Algorithmic Graph Theory. Cambridge University Press, 1985, p. 72, ISBN 978-0-521-28881-1 .
- ↑ David Richeson: The Polyhedral Formula. In: Leonhard Euler: Life, Work and Legacy , p. 428.
- ^ AL Cauchy (1813). Research on les polyèdres - premier mémoire. Journal de l'École Polytechnique. 9 (Cahier 16): pp. 66-86.
- ↑ S.-A.-J. L'Huillier (1861): Mémoire sur la polyèdrométrie. Annales de Mathématiques. 3: 169-89.
- ↑ Andreas Verdun: Leonhard Euler's work on celestial mechanics. Springer, p. 10.
- ↑ David Richeson: The Polyhedral Formula. In: Leonhard Euler: Life, Work and Legacy , pp. 436–437.
- ^ Gerald Alexanderson: Euler and Koenigsberg's bridges: a historical view. Bulletin of the American Mathematical Society. 43 (4), July 2006: 567-573, doi: 10.1090 / S0273-0979-06-01130-X . P. 567.
- ^ Leonhard Euler: Commentarii academiae scientiarum imperialis Petropolitanae. Euler Archives.
- ^ Leonhard Euler: Solutio problematis ad geometriam situs pertinentis . Commentarii academiae scientiarum imperialis Petropolitanae (CASP), Vol. 8.
- ^ Gerald Alexanderson: Euler and Koenigsberg's bridges: a historical view. Bulletin of the American Mathematical Society. 43 (4), July 2006: 567-573, doi: 10.1090 / S0273-0979-06-01130-X . P. 567.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. S. xiv.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 217.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 273.
- ↑ Hui Cheng, KC Gupta: A Historical Note on Final Rotations. In: Journal of Applied Mechanics. Volume 56, No. 1, March 1989, pp. 139-145, doi: 10.1115 / 1.3176034 .
- ^ Leonhard Euler: Formulas generales pro translatione quacunque corporum rigidorum. In: Novi Commentarii academiae scientiarum Petropolitanae. Volume 20 (1775), 1776, pp. 189-207.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler, A Tribute Tricentennial , pp 328-329
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 341.
- ^ RE Bradley: Euler's analysis of the Genoese lottery. 2004.
- ^ Leonhard Euler: Réflections sur une espèce singulière de loterie, nommée Loterie génoise. (E 812).
- ^ DR Bellhouse: Euler and Lotteries. In: Leonhard Euler: Life, Work and Legacy. Pp. 387-388.
- ^ AJ Lotka: Studies on the mode of growth of material aggregates. American Journal of Science, 24, 199-216.
- ^ Enric Cortés: Perspectives on the intrinsic rate of population growth. Methods in Ecology and Evolution, 7 , 2016, 1136-1145, p. 1136.
- ^ John Van Sickle, CAM Attwell and G. Colin Craig: Estimating Population Growth Rate from an Age Distribution of Natural Deaths. The Journal of Wildlife Management, Vol. 51, No. 4 (Oct. 1987), pp. 941-948.
- ↑ Andreas Verdun: Leonhard Euler's work on celestial mechanics. Springer, p. 10.
- ^ SG Langton: Euler on Rigid Bodies. In: Leonhard Euler: Life, Work and Legacy. P. 195.
- ↑ Andreas Verdun: Leonhard Euler's work on celestial mechanics. Springer, p. 11.
- ↑ Andreas Verdun: Leonhard Euler's work on celestial mechanics. Springer, p. 11.
- ↑ Andreas Verdun: Leonhard Euler's work on celestial mechanics. Springer, p. 11.
- ^ Thomas Sonar : 3000 Years of Analysis. Springer, pp. 454-455.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. Pp. 297-298.
- ↑ F. Balck: Euler's essay on the physics of the reaction turbine - an important component in the technical history of water wheels, turbines and other energy conversion machines. Pp. 378-405.
- ↑ Andreas Verdun: Leonhard Euler's work on celestial mechanics. Springer, p. 13.
- ↑ Andreas Verdun: Leonhard Euler's work on celestial mechanics. Springer, p. 283.
- ↑ Ronald S. Calinger: Leonhard Euler: Mathematical Genius in the Enlightenment. Princeton University Press, 2016. ISBN 978-1-4008-6663-2 , p. 384.
- ^ VJ Katz: The Calculus of the Trigonometric Functions. Historia Mathematica, 14: 311-324 (1987).
- ^ C. Wilson: Euler and Applications of Analytical Mathematics to Astronomy. In: Leonhard Euler: Life, Work and Legacy , p. 123.
- ^ Newton: Principia. Book III, Proposition 13.
- ^ Leonhard Euler: Recherches sur le movement des corps céléstes en générale. Mémoires de l'Académie des Sciences de Berlin 3 (1747), 93-143; Leonhard Euler: Opera omnia. Ser. 2, 25, pp. 1-44.
- ^ Leonhard Euler: Recherches sur la question des inégalités du mouvement de Saturne et de Jupiter. Subject propose pour le prix de l'année 1748, par l'Académie Royale des Sciences.
- ^ C. Wilson: Euler and Applications of Analytical Mathematics to Astronomy. In: Leonhard Euler: Life, Work and Legacy , pp. 125–126.
- ↑ Christa Jungnickel, Russell McCormmach: Cavendish - The Experimental Life. P. 155.
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work. In: Leonhard Euler 1707 - 1783: Contributions to life and work. P. 67.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 361.
- ↑ David Speiser: Euler's writings on optics, electricity and magnetism. In: Leonhard Euler 1707–1783: Contributions to life and work. P. 218.
- ↑ Benjamin Robins, Leonhard Euler: New principles of artillery containing the determination of the power of the powder together with an investigation into the difference between the resistance of the air in fast and slow movements. Online at: echo.mpiwg-berlin.mpg.de. (European Cultural Heritage Online), accessed December 24, 2016.
- ↑ Leonhard Euler: Introduction to the Analysis of the Infinite: Part One. Springer Verlag Berlin Heidelberg GmbH, p. 11 (introduction to the reprint edition).
- ↑ Bouger, Euler: For the foundation of the theory of hydrostatic ship stability. In: Yearbook of the Shipbuilding Society. Volume 98, 2004, p. 183.
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work. In: Leonhard Euler 1707 - 1783: Contributions to life and work , p. 26.
- ^ O. Neumann: Cyclotomy: From Euler through Vandermonde to Gauss. In: Leonhard Euler: Life, Work and Legacy , p. 324 ff.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 88.
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work. In: Leonhard Euler 1707 - 1783: Contributions to life and work , p. 40.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 95.
- ↑ Ronald S. Calinger: Leonhard Euler: Mathematical Genius in the Enlightenment. Princeton University Press, 2016, p. 467.
- ↑ Nina I. Nevskaja: Leonhard Euler and astronomy. In: Leonhard Euler 1707 - 1783: Contributions to life and work , pp. 367–368.
- ^ Leonhard Euler: Tentamen novae theoriae musicae ex certissimis harmoniae principiis dilucide expositae. Saint Petersburg 1739.
- ^ Peter Pesic: Music and the Making of Modern Science. P. 133.
- ↑ Daniel Muzzulini: Leonhard Euler consonance. Music theory, 9 (2), p. 2.
- ↑ Daniel Muzzulini: Leonhard Euler consonance. Music theory, 9 (2), p. 6.
- ^ Peter Pesic: Euler's Musical Mathematics. Springer Science + Business Media New York, Volume 35, Number 2, 2013, p. 38.
-
^ Mark Lindley and Ronald Turner-Smith: Mathematical Models of Musical Scales. Bonn, Publishing House for Systematic Musicology, 1993, pp. 234–39.
See also Catherine Nolan: Music Theory and Mathematics. The Cambridge History of Western Music Theory, Th. Christensen ed., New York, CUP, 2002, pp. 278-79. - ↑ Patrice Bailhache: La Musique traduite en Mathématiques: Leonhard Euler. Retrieved February 8, 2020.
- ↑ What is an Euler Fokker genus? Retrieved February 27, 2020.
- ↑ Eric Emery: Temps et musique. Lausanne, L'Âge d'homme, 2000, pp. 344–45.
- ↑ Johannes Mattheson: Large General Bass School. Hamburg, 1731, Vol. I, pp. 104-06, mentioned by Euler; and sample organist rehearsal. Hamburg, 1719, pp. 57-59.
- ^ Wilfrid Perret: Some Questions of Musical Theory. Cambridge, 1926, pp. 60-62; What is Euler-Fokker genus? Retrieved February 8, 2020.
- ^ Leonhard Euler: Tentamen novae theoriae musicae. St Petersburg, 1739, p. 147; De harmoniae veris principiis. St Petersburg, 1774, p. 350.
- ^ Edward Gollin: Combinatorial and Transformational Aspects of Euler's Speculum Musicum. Mathematics and Computation in Music, T. Klouche and Th. Noll eds., Springer, 2009, pp. 406-11.
- ↑ Letters on different subjects in natural philosophy. P. 2.
- ^ Leonhard Euler: Lettres de M. Euler à une princesse d'Allemagne. Lettre I, p. 3.
- ^ Leonhard Euler: Lettres de M. Euler à une princesse d'Allemagne. Lettre XVI, p. 63.
- ↑ Lettres de M. Euler à une princesse d'Allemagne sur différentes questions de physique et de philosophie. Nouvelle Edition, Avec des Additions, par MM. Le Marquis de Condorcet et De La Croix, Paris, 1787.
- ↑ Ronald S Calinger, Ekaterina (Katya) Denisova, Elena N Polyakhova: Leonhard Euler's Letters to a German Princess. IOP Concise Physics, Morgan and Claypool Publishers, 2019, pp. 2-13.
- ^ AP Juskevic, E. Winter: Leonhard Euler and Christian Goldbach: Correspondence. 1729–1764, Akademie-Verlag, Berlin, 1965.
- ↑ Leonhard Euler: Solution d'une question curieuse que ne paroit soumise à aucune analyze. 1766.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 162.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. 162.
- ↑ D. Klyve and L. Stemkoski: Graeco-Latin Squares and a Mistaken Conjecture of Euler. The College Mathematics Journal, Vol. 37, No. 1 (Jan. 2006), 2-15, p. 13.
- ^ Robert E. Bradley, C. Edward Sandifer (eds.): Leonhard Euler: Life, Work and Legacy. Elsevier, 2007, p. 443.
- ^ P. Stäckel, W. Ahrens: The correspondence between CG Jacobi and PH v. Fuss about the publication of the works of Leonhard Euler. Journal for the History of Mathematical Sciences, Leipzig, 1907–1908, p. 235 f.
- ↑ Œuvres complètes de L. Euler. , 5 volumes, Brussels, 1838–1839.
- ^ Henri Bosmans: Sur une tentative d'édition des œuvres complètes de L. Euler faite à Bruxelles en 1839. Louvain 1909.
- ↑ Andreas Kleinert: Leonhardifahrt Euleri Opera Omnia: a centenary project. EMS Newsletter September 2007, p. 26.
- ↑ Andreas Kleinert: Leonhardifahrt Euleri Opera Omnia: a centenary project. EMS Newsletter September 2007, p. 26.
- ^ Emil A. Fellmann: Leonhard Euler: Essay on life and work. In: Leonhard Euler 1707 - 1783: Contributions to life and work , p. 52.
- ^ F. Rudio, K. Schröter: Notes on Swiss cultural history: 21. The bicentenary of Leonhard Euler's birthday; 22. The plan for a complete edition of Euler's works. In: Vierteljahrsschrift der Naturforschenden Gesellschaft in Zürich 52 (1907), pp. 537–546, here: p. 541.
- ↑ Ch. Gehring-Straube: Unrelated times. The Swiss-Soviet relationship between breaking off and resuming relations (1918–1946) based on Swiss files. Zurich 1997.
- ↑ A. Kleinert: Hundred years of Russian-Swiss cooperation on the EULER complete edition. European Science Relations ed. by Dietrich von Engelhardt, Ingrid Kästner, Jürgen Kiefer, Karin Reich (Volume 14), pp. 213–222.
- ↑ See Opera Omnia Leonhard Euler. In: Natural Sciences Switzerland. Retrieved April 12, 2020.
- ^ GI Michajlov and VI Smirnov: Neopublikovannye materialy Leonarda Ėjlera v archive Akademii nauk SSSR. (Unpublished material of Euler in the archive of the Academy of Sciences of the Soviet Union), in: Leonard Ėjler. Sbornik statej v cest '250-letija so dnja rozdenija, predstavlennych Akademii nauk SSSR (Collection of papers in honor of the 250th birthday of Euler). Moscow: Izdatel'stvo Akademii nauk SSSR, cit. P. 47.
- ↑ Rukopisnyematerialy Leonarda Ėjlerav archives Akademiiu nauk SSSR. (Handwritten material of Euler in the Archive of the Academy of Sciences of the Soviet Union), 2 vols. (Trudy Archiva 17 and 20). Moscow-Leningrad: Izdatel'stvo Akademii nauk SSSR 1962, Leningrad: Nauka 1965.
- ↑ The Berlin and Petersburg Academy of Sciences in Leonhard Euler's correspondence. AP Juškevič and E. Winter, eds., In cooperation with P. Hoffmann, TN Klado and Ju. Ch. Kopelevič, 3 Vol. (= Sources and studies on the history of Eastern Europe, III / 1–3). Berlin: Akademie-Verlag 1959, 1961, 1976.
- ^ Leonhard Euler and Christian Goldbach. Correspondence 1829-1764. AP Juškevič and E. Winter, eds., In cooperation with P. Hoffmann, TN Klado and Ju. Ch. Kopelevič (treatises of the German Academy of Sciences in Berlin, class for philosophy, history, political, legal and economic sciences, born 1965, No. 1). Berlin: Akademie-Verlag 1965.
- ↑ L. Ėjler, Pis'ma k učenym (Letters to scholars). Moscow-Leningrad: Izdatel'stvo Akademii nauk SSSR 1963.
- ↑ L. Ėjler: Perepiska. Annotirovannyj ukazatel (Correspondence. Annotated catalog). Leningrad: Nauka 1967.
- ^ Peter Hoffmann: Leonhard Euler and Russia. In: Leonhard Euler: Life, Work and Legacy. Pp. 72-73.
- ^ JJ Burkhardt: The Euler Commission of the Swiss Natural Research Society: A contribution to the history of editions. In: Leonhard Euler 1707-1783. JJ Burckhardt et al., Eds. Birkhäuser, Basel 1983, pp. 501-510.
- ↑ Leonardi Euleri opera omnia, ser. 4. Leonardi Euleri commercium epsitolicum. Vol A1: Descriptio commercii epistolici. Birkhäuser, Basel 1975.
- ^ Peter Hoffmann: Leonhard Euler and Russia. In: Leonhard Euler: Life, Work and Legacy , p. 73.
- ↑ C. Edward Sandifer, Robert E. Bradley: Leonhard Euler: Life, Work and Legacy. Pp. 3-4.
- ^ Herbert Pieper: The Euler of the 19th century: CG Jacob Jacobi. Elements of Mathematics, Swiss Mathematical Society, 2005, p. 98.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. S. xix.
- ↑ Dirk Jan Struik: Outline of the history of mathematics. Springer, p. 139.
- ^ Rüdiger Thiele: Leonhard Euler. Leipzig 1982, pp. 158-160.
- ^ Thomas Sonar: 3000 Years of Analysis. Springer, p. 448.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A tricentennial tribute. P. Vii.
- ↑ Andreas Verdun: Leonhard Euler's work on celestial mechanics. Springer, S. XI.
- ↑ Walter Guatschi: Leonhard Euler: His Life, the Man, and His Works. SIAM Review, Vol. 50, No. 1, pp. 3-33, doi: 10.1137 / 070702710 , p. 3.
- ↑ James J. Tattersall: Elementary Number Theory in Nine Chapters. P. 18.
- ^ W. Dunham: The Genius of Euler: Reflections on His Life and Work. P. 15.
- ↑ Clifford Truesdell: The rational mechanics of flexible elastic bodies 1638–1788. 1960.
- ↑ Hans-Christoph Im Hof, Andreas Kleinert and others: Leonhard Euler, Opera omnia. In: Birkhauser history of science. Online at: Springer.com. Retrieved December 24, 2016.
- ^ Andreas Kleinert, Matthias Mattmüller: Leonhardi Euleri Opera Omnia: a centenary project. EMS Newsletter, September 2007, ISSN 1027-488X (PDF; 1.88 MB), online at: Euler-2007.ch. Retrieved December 24, 2016.
- ↑ Lagrange, œuvre. Volume 14, Gallica.































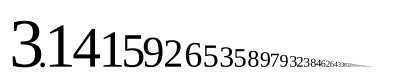






































































































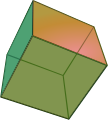













![{\ displaystyle \ int _ {1} ^ {N} {\ frac {1} {x ^ {2}}} \ mathrm {d} x = \ left [- {\ frac {1} {x}} \ right ] _ {1} ^ {N} = 1 - {\ frac {1} {N}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2566a17e1c5d3889f1d3c6bd8fb74822584d5df9)








































![{\ displaystyle {\ sqrt [{12}] {2}} \ approx 1.059463}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40cdb2ae486a0cf1ea97d61be2fa246dbaa2caa2)