L function

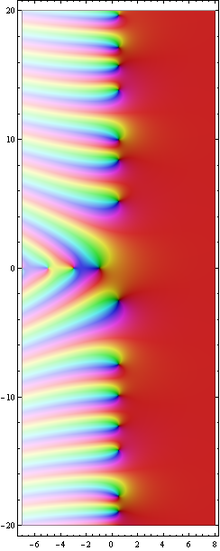
The prototype of all L functions: the Riemann zeta function in the complex plane. The zero, i.e. the origin of the complex plane, is exactly in the middle of the diagram. Different colors encode different arguments of the complex function values. Light color tones indicate function values ​​with a large absolute value, dark color tones a low one close to zero.

L-functions are examined in analytical number theory and mathematical areas based on it. The prototypical example of an L-function is the Riemann zeta-function . L-functions have fundamental properties in common with the Riemann zeta function. So they are generalizations of the Riemann zeta function. The fundamental properties of the Riemann zeta function include:

• the Riemann zeta function agrees in a part of the complex number plane with a Dirichlet series and an Euler product , both of which converge absolutely ;
• The Riemann zeta function, initially only defined in that sub-area, can be analytically extended to a function that is meromorphic on the complex number level ;
• the continued Riemann zeta function satisfies a functional equation of a certain type.

Based on the fundamental work of Leonhard Euler (1707–1783) on what is now known as the Riemann zeta function, the mathematicians Bernhard Riemann (1826–1866), Peter Gustav Dirichlet (1805–1859), Richard Dedekind (1831–1916), Erich Hecke (1887–1947) and Emil Artin (1898–1962) basic subclasses of L-functions, which today have their respective names.

The research search for a general and unambiguous definition of the term "L-function", which makes the desired and in part as yet unproven properties of L-functions provable, has not yet been completed. Rather, it is an important goal of analytical number theory to gain clarity about the most meaningful definition of the term "L-function". In this direction, Atle Selberg (1917–2007) proposed an axiomatic definition of the class of all L-functions in 1992. It has not yet been conclusively clarified whether these or other proposed definitions already include all desirable properties of L-functions and exclude undesired ones. As before, mathematical assumptions (i.e. unproven, but plausible or at least desirable statements about properties of L-functions) shape the theory of L-functions. This continues to be one of the areas of intensive mathematical research.

The two terms “L function” and “Zeta function” are often used synonymously. Nevertheless, not all mathematical functions whose names contain the term “zeta function” are L functions. For example, the primzeta function does not belong to the L-functions because it cannot be analytically extended to the whole complex level.

A first understanding of the subject area of ​​L-functions requires mathematical knowledge in the area of complex numbers , function theory , analytical and algebraic number theory and the representation theory of groups . Such prior knowledge can be partially explained in this article, but not fully presented.

definition

As mentioned in the introduction, there is still no general, unambiguous and widely recognized definition of the term "L-function". The following definition approach follows the approach given by mathematicians Henryk Iwaniec and Emmanuel Kowalski in their textbook on analytical number theory. This definition approach is abstract in places and incomplete in the sense that it does not specify the “arithmetic objects” to which it assigns an “L function”, as well as the exact mechanism of this assignment. However, it includes the properties that are expected of L-functions in general, and thus makes it possible to explain the decisive characteristics of these functions. In addition, further basic concepts of the theory of the L-functions are introduced:

Let it be an arithmetic object - not specified in more detail in this abstract definition, e.g. B. a Dirichlet character or an algebraic number field . A function is assigned to this arithmetic object , which maps complex arguments to complex function values. Iwaniec and Kowalski call such a function an L-function if the following, mathematical objects are assigned (see D-1 to D-6), which meet the following conditions (see B-1 to B-9): ${\displaystyle \textstyle f}$ ${\displaystyle \textstyle f}$ ${\displaystyle \textstyle L(f,s)}$ ${\displaystyle \textstyle s\in \mathbb {C} }$ ${\displaystyle \textstyle L(f,s)}$ ${\displaystyle \textstyle f}$

D-1: Dirichlet series and Euler product

A Dirichlet series is assigned to the arithmetic object ${\displaystyle \textstyle f}$

${\displaystyle \sum _{n\in \mathbb {N} }\lambda (f,n)n^{-s}}$,

which is also called an L series , and an Euler product

${\displaystyle \prod _{p\in \mathbb {P} }(1-\alpha _{1}(f,p)p^{-s})^{-1}\cdot \ldots \cdot (1-\alpha _{d}(f,p)p^{-s})^{-1}}$.

Where is for all natural numbers and . symbolizes the set of all prime numbers . The natural number is called the degree of the Euler product or the degree of the L-function . For every prime and every is . The complex numbers are called local roots or local parameters of at . For a given the expression is called ${\displaystyle \textstyle \lambda (f,n)\in \mathbb {C} }$ ${\displaystyle \textstyle n\in \mathbb {N} }$ ${\displaystyle \textstyle \lambda (f,1)=1}$ ${\displaystyle \textstyle \mathbb {P} }$ ${\displaystyle \textstyle d\in \mathbb {N} }$ ${\displaystyle \textstyle L(f,s)}$ ${\displaystyle \textstyle p}$ ${\displaystyle \textstyle i\in \{1,\ldots ,d\}}$ ${\displaystyle \textstyle \alpha _{i}(f,p)\in \mathbb {C} }$ ${\displaystyle \textstyle \alpha _{i}(f,p)}$ ${\displaystyle \textstyle L(f,s)}$ ${\displaystyle \textstyle p}$ ${\displaystyle p\in \mathbb {P} }$

${\displaystyle (1-\alpha _{1}(f,p)p^{-s})^{-1}\cdot \ldots \cdot (1-\alpha _{d}(f,p)p^{-s})^{-1}}$,

thus the -th factor in the Euler product, the Euler factor of at . ${\displaystyle p}$ ${\displaystyle L(f,s)}$ ${\displaystyle p}$

D-2: gamma factor

In addition, the object has a so-called gamma factor ${\displaystyle \textstyle f}$

${\displaystyle \gamma (f,s)=\pi ^{-ds/2}\prod _{j=1}^{d}\Gamma \left({\frac {s+\kappa _{j}}{2}}\right)}$

assigned, wherein the gamma function , the loop number and the above-mentioned degree of L-function call. The parameters are complex numbers. They are called the local parameters of at infinity or at the infinite prime . ${\displaystyle \textstyle \Gamma }$ ${\displaystyle \textstyle \pi }$ ${\displaystyle \textstyle d}$ ${\displaystyle \textstyle \kappa _{j}}$ ${\displaystyle \textstyle L(f,s)}$

D-3: Guide (Conductor)

A natural number is also assigned to the object ${\displaystyle \textstyle f}$

${\displaystyle q(f)\in \mathbb {N} }$,

the so-called guide or conductor of . Prime numbers that do not divide are called unbranched with respect to . ${\displaystyle \textstyle L(f,s)}$ ${\displaystyle p\in \mathbb {P} }$ ${\displaystyle \textstyle q(f)}$ ${\displaystyle \textstyle L(f,s)}$

D-4: Complete L function

With the help of the Dirichlet series, the gamma factor and the Führer, which are assigned, one now defines the so-called complete L-function of : ${\displaystyle \textstyle f}$ ${\displaystyle \textstyle f}$

${\displaystyle \Lambda (f,s)=q(f)^{s/2}\gamma (f,s)L(f,s).}$

D-5: root number

Furthermore, the object is a complex number ${\displaystyle \textstyle f}$

${\displaystyle \epsilon (f)\in \mathbb {C} }$

assigned. This complex number is called the square root of . ${\displaystyle \textstyle L(f,s)}$

D-6: Dual arithmetic object

Finally, another arithmetic object is assigned that is not specified in more detail in the context of this abstract definition. It is called the dual of and is denoted by. As in the case of are also a Dirichlet series ${\displaystyle \textstyle f}$ ${\displaystyle \textstyle f}$ ${\displaystyle \textstyle {\bar {f}}}$ ${\displaystyle \textstyle f}$ ${\displaystyle \textstyle {\bar {f}}}$

${\displaystyle \sum _{n\in \mathbb {N} }\lambda ({\bar {f}},n)n^{-s}}$,

an Euler product

${\displaystyle \prod _{p\in \mathbb {P} }(1-\alpha _{1}({\bar {f}},p)p^{-s})^{-1}\cdot \ldots \cdot (1-\alpha _{\bar {d}}({\bar {f}},p)p^{-s})^{-1}}$

associated with , a gamma factor and a guide as well as a full L function . Is , it is called self-dual , which means nothing else than for everyone . ${\displaystyle \textstyle {\bar {d}}\in \mathbb {N} }$ ${\displaystyle \textstyle \gamma ({\bar {f}},s)}$ ${\displaystyle \textstyle q({\bar {f}})}$ ${\displaystyle \textstyle \Lambda ({\bar {f}},s)}$ ${\displaystyle \textstyle f={\bar {f}}}$ ${\displaystyle \textstyle L(f,s)}$ ${\displaystyle \textstyle \lambda (f,n)\in \mathbb {R} }$ ${\displaystyle \textstyle n\in \mathbb {N} }$

The above-mentioned objects assigned to the arithmetic object must now meet the following conditions so that the definition of an L-function according to Iwaniec and Kowalski is fulfilled: ${\displaystyle \textstyle f}$ ${\displaystyle \textstyle L(f,s)}$

B-1: Absolute amount of local parameters at ${\displaystyle \textstyle p}$

For every prime and every is . ${\displaystyle \textstyle p}$ ${\displaystyle \textstyle i\in \{1,\ldots ,d\}}$ ${\displaystyle \textstyle |\alpha _{i}(f,p)|<p}$

B-2: Values ​​of local parameters for unbranched ${\displaystyle \textstyle p}$

For all prime numbers that are unbranched with respect to , and all is . ${\displaystyle \textstyle p}$ ${\displaystyle \textstyle L(f,s)}$ ${\displaystyle \textstyle i\in \{1,\ldots ,d\}}$ ${\displaystyle \textstyle \alpha _{i}(f,p)\neq 0}$

B-3: Requirements for the local parameters in infinity

The parameters are either real or occur in the form of complex conjugate pairs in the gamma factor . Also is for each . These last conditions ensure that there are no zeros in and no poles with . denotes the real part of a complex number. ${\displaystyle \textstyle \kappa _{j}}$ ${\displaystyle \textstyle \gamma (f,s)}$ ${\displaystyle \textstyle \Re (\kappa _{j})>-1}$ ${\displaystyle \textstyle j\in \{1,\ldots ,d\}}$ ${\displaystyle \textstyle \gamma (f,s)}$ ${\displaystyle \textstyle \mathbb {C} }$ ${\displaystyle \textstyle \Re (s)\geq 1}$ ${\displaystyle \textstyle \Re }$

B-4: Absolute convergence of the Dirichlet series and the Euler product

Both the Dirichlet series and the Euler product that are assigned converge for absolute . ${\displaystyle \textstyle f}$ ${\displaystyle \textstyle \Re (s)>1}$

B-5: Correspondence of the L-function, Dirichlet series and Euler product in a complex half-plane

The L-function, the Dirichlet series and the Euler product that are assigned coincide in the complex half-plane : ${\displaystyle \textstyle f}$ ${\displaystyle \textstyle \Re (s)>1}$

${\displaystyle L(f,s)=\sum _{n\in \mathbb {N} }\lambda (f,n)n^{-s}=\prod _{p\in \mathbb {P} }(1-\alpha _{1}(f,p)p^{-s})^{-1}\cdot \ldots \cdot (1-\alpha _{d}(f,p)p^{-s})^{-1}.}$

B-6: Analytical continuability and pole positions

The holomorphism of the full L-function in the half-plane already follows from the conditions that the assigned Dirichlet series must meet . But it must also be analytically extendable to a meromorphic function of order 1 on whole , which has poles at most in and . ${\displaystyle \textstyle f}$ ${\displaystyle \textstyle \Lambda (f,s)}$ ${\displaystyle \textstyle \Re (s)>1}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \textstyle s=0}$ ${\displaystyle \textstyle s=1}$

B-7: Absolute amount of the root number

The root number has the absolute value 1. So . ${\displaystyle \textstyle \epsilon (f)\in \mathbb {C} }$ ${\displaystyle \textstyle |\epsilon (f)|=1}$

B-8: Requirements for the objects of the dual associated ${\displaystyle \textstyle f}$

As far as the dual of is concerned, the following must apply: for everyone , as well as and . This means: In the Dirichlet series that is assigned, the coefficients are precisely the complex conjugate numbers of the coefficients in the Dirichlet series that is assigned. The gamma factors and leaders or are associated match. ${\displaystyle \textstyle {\bar {f}}}$ ${\displaystyle \textstyle f}$ ${\displaystyle \textstyle \lambda ({\bar {f}},n)={\bar {\lambda }}(f,n)}$ ${\displaystyle \textstyle n\in \mathbb {N} }$ ${\displaystyle \textstyle \gamma ({\bar {f}},s)=\gamma (f,s)}$ ${\displaystyle \textstyle q({\bar {f}})=q(f)}$ ${\displaystyle \textstyle {\bar {f}}}$ ${\displaystyle \textstyle \lambda }$ ${\displaystyle \textstyle \lambda }$ ${\displaystyle \textstyle f}$ ${\displaystyle \textstyle f}$ ${\displaystyle \textstyle {\bar {f}}}$

B-9: functional equation

The two complete L-functions and are assigned, meet the functional equation ${\displaystyle \textstyle f}$ ${\displaystyle \textstyle {\bar {f}}}$

${\displaystyle \Lambda (f,s)=\epsilon (f)\Lambda ({\bar {f}},1-s)}$

for everyone . ${\displaystyle \textstyle s\in \mathbb {C} }$

Atle Selberg (1917-2007)

The definition approach of Iwaniec and Kowalski reflects the fact that a function that is viewed as an L-function typically occurs as an assignment of the L-function to a mathematical object (e.g. Dirichlet character, algebraic number field). Your approach to definition is abstract and incomplete, as it leaves the question open of what exactly those mathematical objects are and how that assignment should take place.

The definition approach of the Norwegian-American mathematician Atle Selberg from 1992 does not relate to other, mathematical objects . In a non-abstract, unambiguous definition, it specifies a subset of the set of all Dirichlet series, the elements of which must meet certain properties: absolute convergence of the Dirichlet series, analytical continuability, functional equation, Ramanujan conjecture and Euler product. This subset is known today as the Selberg class .

The supreme hypothesis and the motivating background for the definition of the Selberg class is the so-called Great Riemann Hypothesis . Applied to the Selberg class, this assumption says: no zero of an analytical continuation of a Dirichlet series in the Selberg class has a real part greater than 1/2. In the case of the (supposedly) simplest element of the Selberg class (Riemann Dirichlet series including its analytical continuation to the Riemann zeta function), this conjecture corresponds to the Riemann conjecture , which has not been proven or refuted to this day. The Great Riemann Hypothesis has not yet been proven or refuted for any single element of the Selberg class.

Against this background, the still existing inadequacies in the definition of the term "L-function" are to be seen: one would like to define the term "L-function" in such a way that L-functions demonstrably fulfill the Great Riemann Hypothesis - on the other hand, one could so far still not even the simplest case (Riemann hypothesis for the Riemann zeta function) can be proven, which could be a sign of a lack of understanding of the Riemann zeta function and thus make a clear definition of the generalizing term "L-function" difficult.

Examples of L functions

This section gives an overview of basic examples of L-functions.

Riemann zeta function

→ Main article : Riemann zeta function

Bernhard Riemann (1826–1866)

The simplest example of an L-function and at the same time the starting point for every definition of the term “L-function” is the Riemann zeta function . One of the possible "arithmetic objects" in the sense of the definition approach of Iwaniec and Kowalski, to which this L-function can be assigned, is the field of rational numbers . Your Dirichlet range ${\displaystyle \textstyle \zeta }$ ${\displaystyle \textstyle f}$ ${\displaystyle \textstyle \mathbb {Q} }$

${\displaystyle \sum _{n\in \mathbb {N} }{\frac {1}{n^{s}}}\,,}$

so

${\displaystyle \lambda (\mathbb {Q} ,n)=1}$

for all , converges for absolute. Together with their also absolutely convergent Euler product, the following applies to : ${\displaystyle \textstyle n\in \mathbb {N} }$ ${\displaystyle \textstyle \Re (s)>1}$ ${\displaystyle \textstyle \Re (s)>1}$

${\displaystyle \zeta (s)=L(\mathbb {Q} ,s)=\sum _{n\in \mathbb {N} }{\frac {1}{n^{s}}}=\prod _{p\in \mathbb {P} }(1-p^{-s})^{-1}.}$

Riemann zeta function : Contour lines real part ( (s)) = 0, blue, and imaginary part ( (s)) = 0, lilac-colored, for −5 <Re (s) <3 and −25 <Im (s) <65, as well as the "critical straight line" Re (s) = 1/2, brown. For Re (s) <1, the intersections of the blue and lilac-colored contour lines are the zeros of the Riemann zeta function. ${\displaystyle \zeta (s)}$ ${\displaystyle \zeta }$ ${\displaystyle \zeta }$

Since all are real, namely equal to 1, is self-dual. The too dual object is also , thus . ${\displaystyle \textstyle \lambda (\mathbb {Q} ,n)}$ ${\displaystyle \textstyle \zeta (s)}$ ${\displaystyle \textstyle f=\mathbb {Q} }$ ${\displaystyle \textstyle \mathbb {Q} }$ ${\displaystyle \textstyle {\bar {f}}=\mathbb {Q} }$

The degree of the Euler product of the Riemann zeta function is

${\displaystyle d=1}$.

The following applies to your local parameters at : ${\displaystyle \textstyle p}$

${\displaystyle \alpha (\mathbb {Q} ,p)=1}$

for everyone . The following gamma factor is usually used for the Riemann zeta function: ${\displaystyle \textstyle p\in \mathbb {P} }$

${\displaystyle \gamma (\mathbb {Q} ,s)=\pi ^{-{\frac {s}{2}}}\,\Gamma \left({\frac {s}{2}}\right).}$

The local parameter at infinity is then 0. The guide of is ${\displaystyle \textstyle \kappa }$ ${\displaystyle \textstyle \zeta }$

${\displaystyle \textstyle q(\mathbb {Q} )=1}$,

so that the complete Riemann zeta function is the shape

${\displaystyle \Lambda (\mathbb {Q} ,s):=\gamma (\mathbb {Q} ,s)L(\mathbb {Q} ,s)=\pi ^{-{\frac {s}{2}}}\,\Gamma \left({\frac {s}{2}}\right)\zeta (s)}$

accepts. This definition is only valid for, since only in this half-plane the Riemann zeta function can be defined via its Dirichlet series or its Euler product. However, the complete Riemann zeta function has an analytical continuation to a meromorphic function on the whole complex number level. This continuation is holomorphic except for two simple poles in and with the residuals −1 and 1. If one also denotes the continued, complete Riemann zeta function , then it satisfies with the root number ${\displaystyle \textstyle \Re (s)>1}$ ${\displaystyle \textstyle s=0}$ ${\displaystyle \textstyle s=1}$ ${\displaystyle \textstyle \Lambda }$

${\displaystyle \epsilon (\mathbb {Q} )=1}$

the functional equation

${\displaystyle \Lambda (\mathbb {Q} ,s)=\Lambda (\mathbb {Q} ,1-s).}$

This means that the Riemann zeta function, initially only defined by its Dirichlet series or Euler product, has an analytical continuation to a meromorphic function , which is the only one that is not defined, since it has a simple pole there with a residual 1. If the designation is retained for the continued Riemann zeta function, it satisfies the functional equation ${\displaystyle \textstyle \Re (s)>1}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \textstyle s=1}$ ${\displaystyle \textstyle \zeta }$

${\displaystyle \pi ^{-{\frac {s}{2}}}\,\Gamma \left({\frac {s}{2}}\right)\zeta (s)=\pi ^{-{\frac {1-s}{2}}}\,\Gamma \left({\frac {1-s}{2}}\right)\zeta (1-s).}$

The (analytically continued) Riemann zeta function harbors one of the most important questions in analytical number theory, namely the question of the exact position of its so-called non-trivial zeros . These are in the critical strip . The Riemann hypothesis from 1859 - neither proven nor disproved to this day - establishes the thesis that all non-trivial zeros of the Riemann zeta function have the real part 1/2. A proof of this conjecture would allow particularly good estimates of the distribution of the prime numbers. ${\displaystyle \textstyle 0<\Re (s)<1}$

Dirichlet's L functions

→ Main article : Dirichlet's L-function

The closest relatives of the Riemann zeta function are the Dirichlet L functions, which contain the Riemann zeta function as a special case. If all the coefficients in the Dirichlet series belonging to the Riemann zeta function are still 1, then these are defined in Dirichlet's L functions with the help of a Dirichlet character . They take on complex values ​​with the absolute value 1 or are equal to 0. So be a Dirichlet modulo for a ${\displaystyle \lambda }$ ${\displaystyle \textstyle m\in \mathbb {N} }$ ${\displaystyle \textstyle m}$

${\displaystyle \chi :(\mathbb {Z} /m)^{\times }\longrightarrow S^{1}:=\{z\in \mathbb {C} :|z|=1\}}$

Peter Gustav Lejeune Dirichlet (1805-1859)

given, d. H. a group homomorphism from the group of elements of the remainder class ring that can be inverted with respect to multiplication into the circle group of complex numbers with absolute amount 1. Such a Dirichlet character is called primitive and the leader of , if it is not already through a composition ${\displaystyle \textstyle \mathbb {Z} /m}$ ${\displaystyle \textstyle S^{1}}$ ${\displaystyle \textstyle \chi }$ ${\displaystyle \textstyle m}$ ${\displaystyle \textstyle \chi }$

${\displaystyle (\mathbb {Z} /m)^{\times }\longrightarrow (\mathbb {Z} /m')^{\times }\;{\stackrel {\chi '}{\longrightarrow }}\;S^{1}}$

emerges from a Dirichlet character modulo with a real divisor of . With the help of such a Dirichlet character , the following figure is defined, which is also referred to as a Dirichlet character modulo : ${\displaystyle \textstyle \chi '}$ ${\displaystyle \textstyle m'}$ ${\displaystyle \textstyle m'}$ ${\displaystyle \textstyle m}$ ${\displaystyle \textstyle \chi }$ ${\displaystyle \textstyle \chi }$ ${\displaystyle \textstyle m}$

${\displaystyle \chi :{\text{ }}\mathbb {Z} \to \mathbb {C} ,{\text{ }}\chi (n)={\begin{cases}\chi (n\operatorname {mod} m)&{\text{falls}}\quad \operatorname {ggT} (n,m)=1\\0&{\text{falls}}\quad \operatorname {ggT} (n,m)>1.\end{cases}}}$

Dirichlet's L-function to Dirichlet's character modulo 7 with for complex s with −7 <Re (s) <8 and −20 <Im (s) <20: The relationship to the Riemann zeta function is obvious. Nevertheless, there are clear differences: Since it is a non-trivial Dirichlet character, the function shown is complete . So it has no pole like the Riemann zeta function in . Compared to the Riemann zeta function, the real (trivial) zeros are shifted by one unit to the right. They can be seen as black points in −1, −3, −5 etc. in the diagram. The black points in the vertical stripe 0 <Re (s) <1 belong to the infinite number of non-real (non-trivial) zeros of this Dirichlet L-function. The Great Riemann Hypothesis expects each of these non-trivial zeros on the vertical straight line Re (s) = 1/2. ${\displaystyle \textstyle \chi }$ ${\displaystyle \textstyle \chi (3)=\exp(i\pi /3)}$ ${\displaystyle \chi }$ ${\displaystyle s=1}$

The trivial Dirichlet characters modulo have the function value 1, if , otherwise 0. The trivial Dirichlet character modulo 1 is called the main character. He fulfills for everyone . ${\displaystyle \textstyle \chi ^{0}}$ ${\displaystyle m}$ ${\displaystyle \textstyle \operatorname {ggT} (n,m)=1}$ ${\displaystyle \chi (n)=1}$ ${\displaystyle n\in \mathbb {N} }$

If a primitive Dirichlet character is modulo , an L function is assigned to this arithmetic object as follows: With ${\displaystyle \textstyle \chi :\mathbb {Z} \to \mathbb {C} }$ ${\displaystyle \textstyle m}$ ${\displaystyle \chi }$

${\displaystyle \lambda (\chi ,n):=\chi (n)}$

converges the Dirichlet series (also called Dirichlet's L series)

${\displaystyle L(\chi ,s):=\sum _{n\in \mathbb {N} }{\frac {\lambda (\chi ,n)}{n^{s}}}=\sum _{n\in \mathbb {N} }{\frac {\chi (n)}{n^{s}}}}$

for absolutely. With the local parameters at ${\displaystyle \textstyle \Re (s)>1}$ ${\displaystyle \textstyle p}$

${\displaystyle \alpha (\chi ,p):=\chi (p)}$

this also applies to the associated Euler product, and you have the identity

${\displaystyle L(\chi ,s)=\sum _{n\in \mathbb {N} }{\frac {\chi (n)}{n^{s}}}=\prod _{p\in \mathbb {P} }(1-\chi (p)p^{-s})^{-1}}$

for . As is the case with the Riemann zeta function ${\displaystyle \textstyle \Re (s)>1}$

${\displaystyle d=1}$

the degree of the Euler product. If one sets if (in this case means even ), and if (in this case means odd ), then is ${\displaystyle \textstyle \kappa =0}$ ${\displaystyle \textstyle \chi (-1)=1}$ ${\displaystyle \textstyle \chi }$ ${\displaystyle \textstyle \kappa =1}$ ${\displaystyle \textstyle \chi (-1)=-1}$ ${\displaystyle \textstyle \chi }$

${\displaystyle \gamma (\chi ,s)=\pi ^{-{\frac {s}{2}}}\,\Gamma \left({\frac {s+\kappa }{2}}\right)}$

the assigned gamma factor. That then, is the local parameters of the infinite prime spot. The leader of the primitive Dirichlet character is also the leader of Dirichlet's L-function: ${\displaystyle \textstyle \chi }$ ${\displaystyle \textstyle \kappa \in \{0,1\}}$ ${\displaystyle \textstyle m}$ ${\displaystyle \textstyle \chi }$

${\displaystyle q(\chi )=m}$.

The complete Dirichlet L function thus has the form

${\displaystyle \Lambda (\chi ,s):=q(\chi )^{\frac {s}{2}}\gamma (\chi ,s)L(\chi ,s)=\left({\frac {m}{\pi }}\right)^{\frac {s}{2}}\Gamma \left({\frac {s+\kappa }{2}}\right)\sum _{n\in \mathbb {N} }{\frac {\chi (n)}{n^{s}}},}$

a definition that only applies to, since only there the Dirichlet series used converges. Such a complete Dirichlet L-function can, however, be analytically continued on. This creates a whole function if it is a non-trivial Dirichlet character. Otherwise the continued function has a simple pole in with residual 1. The object that is too dual is , that is , the Dirichlet character that arises from by complex conjugation of the function values ​​of , i. H. ${\displaystyle \textstyle \Re (s)>1}$ ${\displaystyle \textstyle \mathbb {C} }$ ${\displaystyle \textstyle \chi }$ ${\displaystyle \textstyle s=1}$ ${\displaystyle \textstyle \chi }$ ${\displaystyle {\overline {\chi }}}$ ${\displaystyle \textstyle \chi }$ ${\displaystyle \textstyle \chi }$

${\displaystyle \textstyle {\overline {\chi }}(n)={\overline {\chi (n)}}}$

for everyone . The root number can be calculated using the Gaussian sum ${\displaystyle \textstyle n\in \mathbb {N} }$ ${\displaystyle \textstyle \epsilon (\chi )}$

${\displaystyle \tau (\chi )=\sum _{x\operatorname {mod} q(\chi )}\chi (x)\exp(2\pi ix/q(\chi ))}$

are calculated, the summation of all residue classes modulo of the guide extends and the circuit number , the imaginary unit and the exponential function call. With ${\displaystyle \textstyle q(\chi )=m}$ ${\displaystyle \textstyle \pi }$ ${\displaystyle \textstyle i}$ ${\displaystyle \exp }$

${\displaystyle \epsilon (\chi )={\begin{cases}{\frac {\tau (\chi )}{\sqrt {q(\chi )}}}&{\text{falls}}\quad \chi (-1)=1\\{\frac {\tau (\chi )}{i{\sqrt {q(\chi )}}}}&{\text{falls}}\quad \chi (-1)=-1\end{cases}}}$

the continued, complete Dirichlet L function then satisfies the functional equation

${\displaystyle \Lambda (\chi ,s)=\epsilon (\chi )\Lambda ({\overline {\chi }},1-s).}$

As required by roots numbers , there is . Dirichlet's L-functions include Riemann's zeta-function, as this arises from the trivial Dirichlet character modulo 1, i.e. the main character. ${\displaystyle \textstyle |\epsilon (\chi )|=1}$ ${\displaystyle \textstyle |\tau (\chi )|={\sqrt {q(\chi )}}}$

In 1837, the German mathematician Peter Gustav Dirichlet used Dirichlet's L-functions, named after him, to prove Dirichlet's prime number theorem, according to which in every arithmetic sequence (also called arithmetic progression )

${\displaystyle a,a\pm n,a\pm 2n,a\pm 3n,\ldots ,{\text{ mit }}\operatorname {ggT} (a,n)=1,{\text{ wobei }}a,n\in \mathbb {N} ,}$

d. H. in every remainder class , there are infinitely many prime numbers. The decisive argument in the proof of Dirichlet's prime number theorem is the realization that this applies to every non-trivial Dirichlet character . ${\displaystyle \textstyle a\operatorname {mod} n}$ ${\displaystyle \textstyle \Lambda (\chi ,1)\neq 0}$ ${\displaystyle \textstyle \chi }$

Dedekind's L-functions

→ Main article : Dedekind's zeta function

The Riemann zeta function refers to the field of rational numbers, the simplest algebraic number field. Dedekind's L-functions generalize this reference to any algebraic number fields, i.e. finite field extensions of such as, for example . So let be an algebraic number field and its degree of expansion over . Be its wholeness ring and its discriminant . Let the number of real embeddings and the number of pairs of complex embeddings of . So it is . ${\displaystyle \textstyle \mathbb {Q} }$ ${\displaystyle \textstyle \mathbb {Q} }$ ${\displaystyle \textstyle \mathbb {Q} ({\sqrt[{3}]{2}})}$ ${\displaystyle K}$ ${\displaystyle n_{K}=[K:\mathbb {Q} ]\in \mathbb {N} }$ ${\displaystyle \mathbb {Q} }$ ${\displaystyle {\mathcal {O}}_{K}}$ ${\displaystyle d_{K}\in \mathbb {Z} }$ ${\displaystyle n_{1}\in \mathbb {N} _{0}}$ ${\displaystyle n_{2}\in \mathbb {N} _{0}}$ ${\displaystyle K}$ ${\displaystyle n_{K}=n_{1}+2n_{2}}$

Richard Dedekind (1831-1916)

Dedekind's L-function (also called Dedekind's zeta-function) relating to is defined by ${\displaystyle K}$ ${\displaystyle \Re (s)>1}$

${\displaystyle \zeta _{K}(s):=L(K,s):=\sum _{0\neq {\mathfrak {a}}\subset {\mathcal {O}}_{K}}{\frac {1}{{\mathcal {N}}({\mathfrak {a}})^{s}}}.}$

In sum, runs through all the zero Ideal different, all ideals of . denotes the absolute norm of . The coefficients of the Dirichlet series ${\displaystyle {\mathfrak {a}}}$ ${\displaystyle \{0\}}$ ${\displaystyle {\mathcal {O}}_{K}}$ ${\displaystyle {\mathcal {N}}({\mathfrak {a}})\in \mathbb {N} }$ ${\displaystyle {\mathfrak {a}}}$

${\displaystyle \sum _{0\neq {\mathfrak {a}}\subset {\mathcal {O}}_{K}}{\frac {1}{{\mathcal {N}}({\mathfrak {a}})^{s}}}=\sum _{n\in \mathbb {N} }{\frac {\lambda (K,n)}{n^{s}}}}$

are so

${\displaystyle \lambda (K,n)=\#\{0\neq {\mathfrak {a}}\subset {\mathcal {O}}_{K}\mid {\mathcal {N}}({\mathfrak {a}})=n\}\in \mathbb {N} _{0}.}$

For each, they indicate the number of whole ideals with absolute norm . In particular, all coefficients are real and therefore self-dual. That Dirichlet series converges for absolute, as does the corresponding Euler product ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle {\mathcal {O}}_{K}}$ ${\displaystyle n}$ ${\displaystyle \lambda (K,n)}$ ${\displaystyle L(K,s)}$ ${\displaystyle \Re (s)>1}$

${\displaystyle \prod _{0\neq {\mathfrak {p}}\subset {\mathcal {O}}_{K}}{\frac {1}{1-{\mathcal {N}}({\mathfrak {p}})^{-s}}}.}$

The product extends over all of the prime ideals of . It applies to identity ${\displaystyle {\mathfrak {p}}}$ ${\displaystyle {\mathcal {O}}_{K}}$ ${\displaystyle \Re (s)>1}$

${\displaystyle L(K,s)=\sum _{0\neq {\mathfrak {a}}\subset {\mathcal {O}}_{K}}{\frac {1}{{\mathcal {N}}({\mathfrak {a}})^{s}}}=\sum _{n\in \mathbb {N} }{\frac {\lambda (K,n)}{n^{s}}}=\prod _{0\neq {\mathfrak {p}}\subset {\mathcal {O}}_{K}}{\frac {1}{1-{\mathcal {N}}({\mathfrak {p}})^{-s}}}.}$

This form of the Euler product does not yet show the individual Euler factors . The degree of the Euler product is in any case the same as the degree of body expansion : ${\displaystyle (1-\alpha _{1}(K,p)p^{-s})^{-1}\cdot \ldots \cdot (1-\alpha _{d}(K,p)p^{-s})^{-1}}$ ${\displaystyle K/\mathbb {Q} }$

${\displaystyle d=[K:\mathbb {Q} ]=n_{K}=n_{1}+2n_{2}.}$

The local parameters depend on the decomposition behavior of the ideals : every ideal has an unambiguous prime ideal decomposition , except for the order of the factors ${\displaystyle \alpha _{j}(K,p)}$ ${\displaystyle (p):=p{\mathcal {O}}_{K}}$ ${\displaystyle (p)}$

${\displaystyle (p)=\prod _{\mathfrak {p}}{\mathfrak {p}}^{e_{\mathfrak {p}}}}$

in prime ideals , in which applies: and for only a finite number of prime ideals . For at most many prime ideals can apply. Such share and to write it . The exponent in the prime ideal decomposition of is called the branching index of over . Is , then applies to one , which is called the index of inertia of over . For each , the branching and inertia indices belonging to the ideal satisfy the following relation to the degree of : ${\displaystyle 0\neq {\mathfrak {p}}\subset {\mathcal {O}}_{K}}$ ${\displaystyle e_{\mathfrak {p}}\in \mathbb {N} _{0}}$ ${\displaystyle e_{\mathfrak {p}}>0}$ ${\displaystyle {\mathfrak {p}}}$ ${\displaystyle n_{K}}$ ${\displaystyle {\mathfrak {p}}}$ ${\displaystyle e_{\mathfrak {p}}>0}$ ${\displaystyle {\mathfrak {p}}}$ ${\displaystyle (p)}$ ${\displaystyle {\mathfrak {p}}|(p)}$ ${\displaystyle e_{\mathfrak {p}}}$ ${\displaystyle (p)}$ ${\displaystyle {\mathfrak {p}}}$ ${\displaystyle p}$ ${\displaystyle {\mathfrak {p}}|(p)}$ ${\displaystyle {\mathcal {N}}({\mathfrak {p}})=p^{f_{\mathfrak {p}}}}$ ${\displaystyle f_{\mathfrak {p}}\in \mathbb {N} }$ ${\displaystyle {\mathfrak {p}}}$ ${\displaystyle p}$ ${\displaystyle p\in \mathbb {P} }$ ${\displaystyle (p)}$ ${\displaystyle K/\mathbb {Q} }$

${\displaystyle \sum _{{\mathfrak {p}}|(p)}e_{\mathfrak {p}}f_{\mathfrak {p}}=n_{K}.}$

With the help of the knowledge of the indices of inertia for each , the local parameters can now be determined, namely via the factors in the identity ${\displaystyle p\in \mathbb {P} }$ ${\displaystyle \alpha _{j}(K,p)}$ ${\displaystyle (1-p^{-sf_{\mathfrak {p}}})^{-1}}$

${\displaystyle \prod _{0\neq {\mathfrak {p}}\subset {\mathcal {O}}_{K}}{\frac {1}{1-{\mathcal {N}}({\mathfrak {p}})^{-s}}}=\prod _{p\in \mathbb {P} }\;\prod _{{\mathfrak {p}}|(p)}(1-p^{-sf_{\mathfrak {p}}})^{-1},}$

by factoring the polynomials in the polynomial ring . ${\displaystyle X^{f_{\mathfrak {p}}}-1}$ ${\displaystyle \mathbb {C} [X]}$

The gamma factor with respect to is ${\displaystyle L(K,s)}$

${\displaystyle \gamma (K,s)=\pi ^{-{\frac {s\cdot n_{K}}{2}}}\,\Gamma \left({\frac {s}{2}}\right)^{n_{1}+n_{2}}\,\Gamma \left({\frac {s+1}{2}}\right)^{n_{2}}.}$

The amount of the discriminant of is the conductor of : ${\displaystyle K}$ ${\displaystyle L(K,s)}$

${\displaystyle q(K)=|d_{K}|.}$

Thus the complete L-function of for is given by ${\displaystyle K}$ ${\displaystyle \Re (s)>1}$

${\displaystyle \Lambda (K,s):=q(K)^{\frac {s}{2}}\,\gamma (K,s)\,L(K,s)=\left({\frac {|d_{K}|}{\pi ^{n_{K}}}}\right)^{\frac {s}{2}}\,\Gamma \left({\frac {s}{2}}\right)^{n_{1}+n_{2}}\,\Gamma \left({\frac {s+1}{2}}\right)^{n_{2}}\,\sum _{0\neq {\mathfrak {a}}\subset {\mathcal {O}}_{K}}{\frac {1}{{\mathcal {N}}({\mathfrak {a}})^{s}}}.}$

This has an analytical continuation on the complex number level with simple poles at and and the residuals or there  . Here is the number of infinite digits, the class number and the regulator of as well as the number of roots of unity that lie in. ${\displaystyle s=0}$ ${\displaystyle s=1}$ ${\displaystyle -{\frac {2^{r}hR}{w}}}$ ${\displaystyle {\frac {2^{r}hR}{w}}}$ ${\displaystyle r=n_{1}+n_{2}}$ ${\displaystyle h\in \mathbb {N} }$ ${\displaystyle R\in \mathbb {R} }$ ${\displaystyle K}$ ${\displaystyle w\in \mathbb {N} }$ ${\displaystyle K}$

Dedekind's L-functions always have the root number 1:

${\displaystyle \epsilon (K)=1.}$

Thus the analytically continued, complete L-function of the functional equation is sufficient ${\displaystyle K}$

${\displaystyle \Lambda (K,s)=\Lambda (K,1-s).}$

The analytically continued function now also permits the analytical continuation of , namely through the definition ${\displaystyle \Lambda (K,s)}$ ${\displaystyle L(K,s)}$

${\displaystyle L(K,s):={\frac {\Lambda (K,s)}{|d_{k}|^{\frac {s}{2}}\,\gamma (K,s)}}=\left({\frac {\pi ^{n_{K}}}{|d_{K}|}}\right)^{\frac {s}{2}}\cdot {\frac {\Lambda (K,s)}{\Gamma \left({\frac {s}{2}}\right)^{n_{1}+n_{2}}\,\Gamma \left({\frac {s+1}{2}}\right)^{n_{2}}}}.}$

This turns into a meromorphic function on with a simple pole in . One of its fascinating properties is the so-called analytic class number formula , according to which the residual of in takes on the following form: ${\displaystyle L(K,s)}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle s=1}$ ${\displaystyle L(K,s)}$ ${\displaystyle s=1}$

${\displaystyle \operatorname {Res} _{s=1}\,L(K,s)={\frac {2^{n_{1}}(2\pi )^{n_{2}}}{w{\sqrt {|d_{K}|}}}}\,hR.}$

Hedge ash L functions

Heckesche L-functions are common generalizations of Dirichlet's and Dedekind's L-functions. On the one hand, they refer to arbitrary algebraic number fields (like Dedekind's L-functions) and, on the other hand, depend on suitable characters (like Dirichlet's L-functions). The German mathematician Erich Hecke defined the L-functions named after him with the help of so-called size characters and was able to prove the properties desired for L-functions. The more modern approach to L-functions with reference to any algebraic number fields and suitable characters, which can also be generalized to a large extent, uses ideal class characters .

L-functions for size characters

Heckesche L-rows to size characters have the shape

Erich Hecke (1887–1947)

${\displaystyle L(\chi ,s)=\sum _{0\neq {\mathfrak {a}}\subset {\mathcal {O}}_{K}}{\frac {\chi ({\mathfrak {a}})}{{\mathcal {N}}({\mathfrak {a}})^{s}}}.}$

As with Dedekind's L-functions, denotes an algebraic number field with a wholeness ring and degree of expansion . The sum runs through all of the whole ideals of which differ from the zero ideal and denotes the absolute norm of . The complex values are based on a character (i.e. group homomorphism) ${\displaystyle K}$ ${\displaystyle {\mathcal {O}}_{K}}$ ${\displaystyle n:=n_{K}=[K:\mathbb {Q} ]\in \mathbb {N} }$ ${\displaystyle {\mathfrak {a}}}$ ${\displaystyle K}$ ${\displaystyle {\mathcal {N}}({\mathfrak {a}})\in \mathbb {N} }$ ${\displaystyle {\mathfrak {a}}}$ ${\displaystyle \chi ({\mathfrak {a}})}$

${\displaystyle \chi :\;J^{\mathfrak {m}}\;\longrightarrow \;S^{1}:=\{z\in \mathbb {C} :|z|=1\}.}$

Here is a whole ideal of and symbolizes the group of partially foreign, broken ideals of . That means: a broken ideal of lies in if and only if the exponent of in the prime ideal decomposition is equal to 0 for all prime ideals of that divide the whole ideal (i.e. ). The group generalizes the groups used in Dirichlet's L-functions . ${\displaystyle {\mathfrak {m}}}$ ${\displaystyle {\mathcal {O}}_{K}}$ ${\displaystyle J^{\mathfrak {m}}}$ ${\displaystyle {\mathfrak {m}}}$ ${\displaystyle K}$ ${\displaystyle {\mathfrak {b}}}$ ${\displaystyle K}$ ${\displaystyle J^{\mathfrak {m}}}$ ${\displaystyle {\mathfrak {p}}}$ ${\displaystyle {\mathfrak {b}}}$ ${\displaystyle {\mathfrak {p}}}$ ${\displaystyle K}$ ${\displaystyle {\mathfrak {m}}}$ ${\displaystyle {\mathfrak {p}}\supseteq {\mathfrak {m}}}$ ${\displaystyle J^{\mathfrak {m}}}$ ${\displaystyle (\mathbb {Z} /m)^{\times }}$

If there is any such character and if one sets for all ideals that are not coprime , then the L-series given above converges absolutely in the half-plane . Because of the uniqueness of the prime ideal decomposition of ideals into , the following equality applies with the associated Euler product, which runs through all non-zero prime ideals of : ${\displaystyle \chi :\;J^{\mathfrak {m}}\;\longrightarrow \;S^{1}}$ ${\displaystyle \chi ({\mathfrak {a}})=0}$ ${\displaystyle {\mathfrak {a}}}$ ${\displaystyle {\mathfrak {m}}}$ ${\displaystyle L(\chi ,s)}$ ${\displaystyle \Re (s)>1}$ ${\displaystyle {\mathcal {O}}_{K}}$ ${\displaystyle {\mathfrak {p}}}$ ${\displaystyle {\mathcal {O}}_{K}}$

${\displaystyle L(\chi ,s)=\sum _{0\neq {\mathfrak {a}}\subset {\mathcal {O}}_{K}}{\frac {\chi ({\mathfrak {a}})}{{\mathcal {N}}({\mathfrak {a}})^{s}}}=\prod _{0\neq {\mathfrak {p}}\subset {\mathcal {O}}_{K}}{\frac {1}{1-\chi ({\mathfrak {p}}){\mathcal {N}}({\mathfrak {p}})^{-s}}}.}$

The real challenge now lies in a suitable selection of the characters so that the properties typical for L-functions can be proven. The characters with these desirable properties are called magnitudes : A magnitude modulo of a whole ideal of the algebraic number field is a group homomorphism ${\displaystyle \chi :\;J^{\mathfrak {m}}\;\longrightarrow \;S^{1}}$ ${\displaystyle {\mathfrak {m}}}$ ${\displaystyle K}$

${\displaystyle \chi :\;J^{\mathfrak {m}}\longrightarrow \;S^{1},\;\;{\mathfrak {b}}\longmapsto \chi ({\mathfrak {b}}),}$

to which there are two characters

${\displaystyle \chi _{e}:\;({\mathcal {O}}_{K}/{\mathfrak {m}})^{\star }\longrightarrow S^{1}\;{\text{ und }}\;\chi _{\infty }:\;{\bf {R}}^{\star }\longrightarrow S^{1}}$

so that for all numbers that are coprime : ${\displaystyle {\mathfrak {m}}}$ ${\displaystyle a\in {\mathcal {O}}_{K}}$

${\displaystyle \chi ((a))=\chi _{e}(a)\,\chi _{\infty }(a).}$

To explain this definition:

• ${\displaystyle ({\mathcal {O}}_{K}/{\mathfrak {m}})^{\star }}$symbolizes the unit group of the remainder class ring modulo , thus consists of all elements of that are invertible. ${\displaystyle {\mathcal {O}}_{K}}$ ${\displaystyle {\mathfrak {m}}}$ ${\displaystyle {\mathcal {O}}_{K}/{\mathfrak {m}}}$

• ${\displaystyle {\bf {R}}}$denotes the Minkowski space with respect to . Is the set of all embeddings , there is from all tuples , with for all . Addition and multiplication in -dimensional - algebra are defined component-wise. The picture of the embedding function is in . The multiplicative group consists of all elements of where all components are different from zero. Is , so is for everyone , because the embeddings are body homomorphisms . The group homomorphism embeds the multiplicative group in the multiplicative group . ${\displaystyle K}$ ${\displaystyle X}$ ${\displaystyle \tau :\;K\hookrightarrow \mathbb {C} }$ ${\displaystyle {\bf {R}}}$ ${\displaystyle n}$ ${\displaystyle (z_{\tau })_{\tau \in X}}$ ${\displaystyle z_{\tau }\in \mathbb {C} }$ ${\displaystyle z_{\overline {\tau }}={\overline {(z_{\tau })}}}$ ${\displaystyle \tau \in X}$ ${\displaystyle n}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle {\bf {R}}}$ ${\displaystyle K\ni a\mapsto (\tau (a))_{\tau \in X}}$ ${\displaystyle {\bf {R}}}$ ${\displaystyle {\bf {R}}^{\star }}$ ${\displaystyle {\bf {R}}}$ ${\displaystyle a\in K^{\star }:=K\setminus \{0\}}$ ${\displaystyle \tau (a)\neq 0}$ ${\displaystyle \tau \in X}$ ${\displaystyle \tau \in X}$ ${\displaystyle \iota _{\infty }:\;K^{\star }\rightarrow {\bf {R}}^{\star },\;a\mapsto \iota _{\infty }(a):=(\tau (a))_{\tau \in X}}$ ${\displaystyle K^{\star }}$ ${\displaystyle {\bf {R}}^{\star }}$

• An element is called coprime to the whole ideal if the main ideal is coprime to . Denotes the group of to prime elements and to two relatively prime , we have the well-defined group homomorphism , that to the quotient of the residue classes of and modulo mapping. ${\displaystyle a\in K^{\star }}$ ${\displaystyle {\mathfrak {m}}}$ ${\displaystyle (a):=a{\mathcal {O}}_{K}}$ ${\displaystyle {\mathfrak {m}}}$ ${\displaystyle K^{({\mathfrak {m}})}:=\{a\in K^{\star }\mid (a,{\mathfrak {m}})=1\}}$ ${\displaystyle {\mathfrak {m}}}$ ${\displaystyle a\in K^{\star }}$ ${\displaystyle a=b/c}$ ${\displaystyle {\mathfrak {m}}}$ ${\displaystyle b,c\in {\mathcal {O}}_{K}}$ ${\displaystyle \iota _{e}:\;K^{({\mathfrak {m}})}\rightarrow ({\mathcal {O}}_{K}/{\mathfrak {m}})^{\star }}$ ${\displaystyle a\mapsto [b+{\mathfrak {m}}]/[c+{\mathfrak {m}}]}$ ${\displaystyle a=b/c}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle {\mathfrak {m}}}$

• According to its definition, the main ideal, which is to be coprime, breaks down into a "finite" character and an "infinite" character . Correctly, this decomposition condition would have to be replaced by and by , which is always omitted for the sake of brevity. and are clearly determined by. ${\displaystyle \chi }$ ${\displaystyle {\mathfrak {m}}}$ ${\displaystyle (a)\subset {\mathcal {O}}_{K}}$ ${\displaystyle \chi _{e}}$ ${\displaystyle \chi _{\infty }}$ ${\displaystyle \chi _{e}(a)}$ ${\displaystyle \chi _{e}(\iota _{e}(a))}$ ${\displaystyle \chi _{\infty }(a)}$ ${\displaystyle \chi _{\infty }(\iota _{\infty }(a))}$ ${\displaystyle \chi _{e}}$ ${\displaystyle \chi _{\infty }}$ ${\displaystyle \chi }$

A character of magnitude modulo is called primitive if it is not used as a restriction ${\displaystyle {\mathfrak {m}}}$

${\displaystyle \chi =\chi '|_{J^{m}}:J^{\mathfrak {m}}\longrightarrow S^{1}}$

of a size character can be represented modulo , in which the whole ideal is a real divisor of the whole ideal . is not primitive if and only if its "finite" character is over- factored, i.e. H. if as a compound word ${\displaystyle \chi ':\,J^{{\mathfrak {m}}'}\rightarrow S^{1}}$ ${\displaystyle {\mathfrak {m}}'}$ ${\displaystyle {\mathfrak {m}}'}$ ${\displaystyle {\mathfrak {m}}}$ ${\displaystyle \chi }$ ${\displaystyle \chi _{e}}$ ${\displaystyle ({\mathcal {O}}_{K}/{\mathfrak {m}}')^{\star }}$ ${\displaystyle \chi _{e}}$

${\displaystyle \chi _{e}:\;({\mathcal {O}}_{K}/{\mathfrak {m}})^{\star }\longrightarrow ({\mathcal {O}}_{K}/{\mathfrak {m}}')^{\star }\;{\stackrel {\chi _{e}'}{\longrightarrow }}\;S^{1}}$

can be written in which the "finite" character of a magnitude is modulo with a real divisor of . The leader of a size character modulo is the smallest divisor of , so that it can be represented as a limitation of a size character . The leader of can also be defined in terms of the "finite" character of : is the smallest divisor of such that over factorized. ${\displaystyle \chi _{e}'}$ ${\displaystyle \chi '}$ ${\displaystyle {\mathfrak {m}}'}$ ${\displaystyle {\mathfrak {m}}'}$ ${\displaystyle {\mathfrak {m}}}$ ${\displaystyle \chi }$ ${\displaystyle {\mathfrak {m}}}$ ${\displaystyle {\mathfrak {f}}}$ ${\displaystyle {\mathfrak {m}}}$ ${\displaystyle \chi }$ ${\displaystyle \chi '|_{J^{\mathfrak {m}}}}$ ${\displaystyle \chi ':J^{\mathfrak {f}}\rightarrow S^{1}}$ ${\displaystyle \chi }$ ${\displaystyle \chi _{e}}$ ${\displaystyle \chi }$ ${\displaystyle {\mathfrak {f}}}$ ${\displaystyle {\mathfrak {m}}}$ ${\displaystyle \chi _{e}}$ ${\displaystyle ({\mathcal {O}}_{K}/{\mathfrak {f}})^{\star }}$

With the help of the concept of a primitive size character, all objects typical for L-functions can now be defined and the desired statements can be demonstrated: completed Heckesche L-function, analytical continuation, leader, root number and functional equation. This is the path that Erich Hecke has taken and is described in detail in Neukirch's textbook. However, this approach uses mathematical objects ( ideal numbers ), which can be considered obsolete from today's perspective and which obscure the actual essence of the completed Heckeschen L-functions.

L functions for idle class characters

The more modern theory for the treatment of Heckeschen L-functions, which can also be generalized to a large extent, is known as Tate's Thesis (doctoral thesis by the American mathematician John T. Tate ). This theory uses ideal class characters instead of primitive size characters, for the definition of which the terms nobility and ideal are needed: Let be an algebraic number field and ${\displaystyle K}$

John T. Tate (1925-2019)

${\displaystyle \mathbb {A} :=\mathbb {A} _{K}:=\prod _{v}'K_{v}}$

the ring of nobles from . The infinite set of all digits runs through it , i. H. the set of all equivalence classes of non-trivial absolute values of . denotes the complete envelope (completion) of regarding . The ellipsis on the product symbol shows the restriction in comparison to the direct product that in every nobility for almost all (i.e. for all but a maximum of finitely many) places the component has to be in the ring of the whole elements of . The canonical embedding homomorphism , for all , is well-defined since each is whole for almost all places . The elements of the multiplicative group of units (invertible elements) of are called the idels of . You can also write as a restricted product: ${\displaystyle K}$ ${\displaystyle v}$ ${\displaystyle K}$ ${\displaystyle K_{v}}$ ${\displaystyle K}$ ${\displaystyle v}$ ${\displaystyle \prod _{v}K_{v}}$ ${\displaystyle (x_{v})_{v}\in \mathbb {A} }$ ${\displaystyle v}$ ${\displaystyle x_{v}\in K_{v}}$ ${\displaystyle {\mathcal {O}}_{v}}$ ${\displaystyle v}$ ${\displaystyle K_{v}}$ ${\displaystyle K\hookrightarrow \mathbb {A} ,\;x\mapsto (x_{v})_{v}}$ ${\displaystyle x_{v}=x}$ ${\displaystyle v}$ ${\displaystyle x\in K}$ ${\displaystyle v}$ ${\displaystyle \mathbb {A} ^{\times }}$ ${\displaystyle \mathbb {A} }$ ${\displaystyle K}$ ${\displaystyle \mathbb {A} ^{\times }}$

${\displaystyle \mathbb {A} ^{\times }=\prod _{v}'K_{v}^{\times }}$.

Here the ellipsis means that an element of the direct product is an ideal if and only if applies to almost all places . Virtue , , for all , the unit can group by embedding into the group of Idele, one that as a subgroup of Idelgruppe can consider the elements of the Hauptidele of be named. The quotient group is called the ideal class group of . Ideal group and ideal class group are provided with suitable topologies so that one can then speak of continuous mapping. An ideal class character of is a continuous group homomorphism ${\displaystyle (x_{v})_{v}}$ ${\displaystyle \prod _{v}K_{v}}$ ${\displaystyle x_{v}\in {\mathcal {O}}_{v}^{\times }}$ ${\displaystyle v}$ ${\displaystyle K^{\times }\hookrightarrow \mathbb {A} ^{\times }}$ ${\displaystyle x\mapsto (x_{v})_{v}}$ ${\displaystyle x_{v}=x}$ ${\displaystyle v}$ ${\displaystyle K}$ ${\displaystyle K^{\times }}$ ${\displaystyle \mathbb {A} ^{\times }}$ ${\displaystyle K}$ ${\displaystyle \mathbb {A} ^{\times }/K^{\times }}$ ${\displaystyle K}$ ${\displaystyle K}$

${\displaystyle \chi :\mathbb {A} ^{\times }\longrightarrow \mathbb {C} ^{\times }}$,

which is trivial, i.e. only takes the value 1 there. In this respect, one can also understand the character of the ideal class group, which justifies the name "ideal class character". Such a character always has a decomposition ${\displaystyle K^{\times }\hookrightarrow \mathbb {A} ^{\times }}$ ${\displaystyle \chi }$ ${\displaystyle \mathbb {A} ^{\times }/K^{\times }\rightarrow \mathbb {C} ^{\times }}$

${\displaystyle \chi =\prod _{v}'\chi _{v}}$

in local characters that for almost all points of unbranched. This is indicated by the ellipsis on the product symbol. A local character is called unbranched if its restriction to trivial is branched otherwise . ${\displaystyle \chi _{v}:K_{v}^{\times }\rightarrow \mathbb {C} ^{\times }}$ ${\displaystyle v}$ ${\displaystyle K}$ ${\displaystyle \chi _{v}}$ ${\displaystyle {\mathcal {O}}_{v}^{\times }}$

The leader of an ideal class character is a whole ideal in , viz ${\displaystyle {\mathfrak {f}}(\chi )}$ ${\displaystyle {\mathcal {O}}_{K}}$

${\displaystyle {\mathfrak {f}}(\chi )=\prod _{v\not \mid \infty }{\mathfrak {p}}_{v}^{a(\chi _{v})}.}$

The product passes through all finite places of . is that through certain prime ideals. The exponents are in . If it is unbranched, then nothing is or contributes to the leader. If it is branched, then is the smallest natural number , so that on is trivial. It denotes a uniformizing element. ${\displaystyle K}$ ${\displaystyle {\mathfrak {p}}_{v}}$ ${\displaystyle v}$ ${\displaystyle a(\chi _{v})}$ ${\displaystyle \mathbb {N} _{0}}$ ${\displaystyle \chi _{v}}$ ${\displaystyle a(\chi _{v})=0}$ ${\displaystyle {\mathfrak {p}}_{v}^{a(\chi _{v})}}$ ${\displaystyle \chi _{v}}$ ${\displaystyle a(\chi _{v})}$ ${\displaystyle k\geq 1}$ ${\displaystyle \chi _{v}}$ ${\displaystyle 1+\pi _{v}^{k}{\mathcal {O}}_{v}}$ ${\displaystyle \pi _{v}\in {\mathcal {O}}_{v}}$

The (incomplete) L-function for the ideal class character is defined by ${\displaystyle \chi }$

${\displaystyle L(\chi ,s):=\prod _{v\not \mid \infty }'(1-\chi _{v}(\pi _{v})q_{v}^{-s})^{-1}}$.

The product is formed over all finite places of for which is unbranched. denotes the order of the remainder class field . Since it is unbranched, the value of does not depend on the choice of the uniformizing element . The product on the right side of the definition of converges absolutely in a right half plane of the complex number plane. ${\displaystyle v}$ ${\displaystyle K}$ ${\displaystyle \chi }$ ${\displaystyle q_{v}}$ ${\displaystyle {\mathcal {O}}_{v}/(\pi _{v})}$ ${\displaystyle \chi _{v}}$ ${\displaystyle \chi _{v}(\pi _{v})}$ ${\displaystyle \pi _{v}}$ ${\displaystyle L(\chi ,s)}$

To complete the , L-factors are still required at the infinite places: ${\displaystyle L(\chi ,s)}$

${\displaystyle L_{\infty }(\chi ,s):=\prod _{v\mid \infty }L(\chi _{v},s)}$.

If there is a real, infinite place, the completion is the same . The local character can thus be identified with a character . The latter necessarily has the form with clearly defined numbers and . The L-factor at the real, infinite point is then defined by ${\displaystyle v}$ ${\displaystyle K_{v}}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \chi _{v}:K_{v}^{\times }\rightarrow \mathbb {C} ^{\times }}$ ${\displaystyle \mathbb {R} ^{\times }\rightarrow \mathbb {C} ^{\times }}$ ${\displaystyle t\mapsto |t|^{s_{0}}(t/|t|)^{m}}$ ${\displaystyle s_{0}\in \mathbb {C} }$ ${\displaystyle m\in \{0,1\}}$ ${\displaystyle v}$

${\displaystyle L(\chi _{v},s):=\Gamma _{\mathbb {R} }(s+s_{0}+m),\;\Gamma _{\mathbb {R} }(z):=\pi ^{-z/2}\Gamma (z/2).}$

If there is a non-real, infinite, i.e. complex place, then is isomorphic to , and there are two ways of identifying with . You choose one of them and can then take it as a character . Such a character of always has the form with clearly defined numbers and . The corresponding L-factor is then given by ${\displaystyle v}$ ${\displaystyle K_{v}}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle K_{v}}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \chi _{v}:K_{v}^{\times }\rightarrow \mathbb {C} ^{\times }}$ ${\displaystyle \mathbb {C} ^{\times }\rightarrow \mathbb {C} ^{\times }}$ ${\displaystyle \mathbb {C} ^{\times }}$ ${\displaystyle t\mapsto |t|^{2s_{0}}(t/|t|)^{m}}$ ${\displaystyle s_{0}\in \mathbb {C} }$ ${\displaystyle m\in \mathbb {Z} }$ ${\displaystyle v}$

${\displaystyle L(\chi _{v},s):=\Gamma _{\mathbb {C} }(s+s_{0}+|m|/2),\;\Gamma _{\mathbb {C} }(z):=2\cdot (2\pi )^{-z}\Gamma (z).}$

The complete L-function for the ideal class character is now defined as ${\displaystyle \chi }$

${\displaystyle \Lambda (\chi ,s):={\big (}|d_{K}|\cdot {\mathcal {N}}{\mathfrak {f(\chi )}}{\big )}^{s/2}\cdot L_{\infty }(\chi ,s)\cdot L(\chi ,s)}$,

with the absolute value of the discriminant of and the norm of the leader of . The leader of the L-function is thus composed of the absolute value of the discriminant of the number field and the norm of the leader of the ideal class character : ${\displaystyle |d_{K}|}$ ${\displaystyle K}$ ${\displaystyle {\mathcal {N}}{\mathfrak {f(\chi )}}}$ ${\displaystyle \chi }$ ${\displaystyle \Lambda (\chi ,s)}$ ${\displaystyle K}$ ${\displaystyle \chi }$

${\displaystyle q(\chi ):=|d_{K}|\cdot {\mathcal {N}}{\mathfrak {f(\chi )}}}$.

The degree of is the degree of body expansion : ${\displaystyle \Lambda (\chi ,s)}$ ${\displaystyle K/\mathbb {Q} }$

${\displaystyle d:=[K:\mathbb {Q} ]}$.

As far as the functional equation of the complete L-function is concerned, there is a real number and a root number with such that: ${\displaystyle \Lambda (\chi ,s)}$ ${\displaystyle r}$ ${\displaystyle \epsilon (\chi )\in \mathbb {C} }$ ${\displaystyle |\epsilon (\chi )|=1}$

${\displaystyle \Lambda (\chi ,s)=\epsilon (\chi )\Lambda ({\overline {\chi }},r-s).}$

If a unitary ideal class character, i.e. if its image lies on the unit circle , then it is . ${\displaystyle \chi :\mathbb {A} ^{\times }\rightarrow \mathbb {C} ^{\times }}$ ${\displaystyle {\mathcal {S}}^{1}}$ ${\displaystyle r=1}$

Artinian L functions

The examples of L-functions listed so far relate directly to individual algebraic number fields and associated characters. On the other hand, Artin's L-functions are assigned to the representations of the Galois group of a Galois body expansion. They are closely related to the L-functions mentioned above, but generalize them considerably. The initial observation, which motivates the definition of Artin's L-functions, considers the isomorphism

${\displaystyle (\mathbb {Z} /m\mathbb {Z} )^{\times }\;{\stackrel {\sim }{\longrightarrow }}\;G(\mathbb {Q} (\mu _{m})/\mathbb {Q} )}$

between the group of invertible residue classes of the residue class ring , and the Galois group of the cyclotomic body of th roots of unity. This group isomorphism assigns the remainder class of a prime number with the Frobenius automorphism , which maps every -th unity root to and is thereby determined. With the help of this isomorphism, a Dirichlet character can also be understood as a character . can be used as the general linear array of one-dimensional - vector space are interpreted. A one-dimensional representation is thus obtained from the original Dirichlet character ${\displaystyle \mathbb {Z} /m\mathbb {Z} }$ ${\displaystyle m\in \mathbb {N} }$ ${\displaystyle \mathbb {Q} (\mu _{m})}$ ${\displaystyle m}$ ${\displaystyle p\operatorname {mod} m}$ ${\displaystyle p}$ ${\displaystyle p\not \mid m}$ ${\displaystyle \phi _{p}:\mathbb {Q} (\mu _{m})/\mathbb {Q} \rightarrow \mathbb {Q} (\mu _{m})/\mathbb {Q} }$ ${\displaystyle m}$ ${\displaystyle \zeta }$ ${\displaystyle \zeta ^{p}}$ ${\displaystyle \chi :(\mathbb {Z} /m\mathbb {Z} )^{\times }\rightarrow \mathbb {C} ^{\times }}$ ${\displaystyle \chi :G(\mathbb {Q} (\mu _{m})/\mathbb {Q} )\rightarrow \mathbb {C} ^{\times }}$ ${\displaystyle \mathbb {C} ^{\times }}$ ${\displaystyle GL_{1}(\mathbb {C} )}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$

${\displaystyle \chi :G(\mathbb {Q} (\mu _{m})/\mathbb {Q} )\longrightarrow GL_{1}(\mathbb {C} )}$,

with the help of which the L series assigned to the Dirichlet character can also be written in the form:

${\displaystyle L(\chi ,s)=\prod _{p\not \mid m}(1-\chi (\phi _{p})p^{-s})^{-1}}$.

Emil Artin (1898–1962)

Based on this initial observation, Artin's L-series are defined as follows: Let us be a finite, Galois extension of number fields with a Galois group , a finite-dimensional vector space and ${\displaystyle E/K}$ ${\displaystyle G:=G(E/K)}$ ${\displaystyle V}$ ${\displaystyle \mathbb {C} }$

${\displaystyle \rho :G\longrightarrow GL(V),\;\sigma \longmapsto \rho (\sigma ),}$

a representation of , i.e. a group homomorphism of the Galois group into the general, linear group of vector space automorphisms of . Let now be a non-zero prime ideal of and a prime ideal of that lies above , i.e. H. is a factor in the prime ideal decomposition of the ideal of the whole ring of . The decomposition group from over is the subgroup of the Galois group . One has a canonical, surjective group homomorphism ${\displaystyle (\rho ,V)}$ ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle GL(V)}$ ${\displaystyle V}$ ${\displaystyle {\mathfrak {p}}}$ ${\displaystyle K}$ ${\displaystyle {\mathfrak {P}}}$ ${\displaystyle E}$ ${\displaystyle {\mathfrak {p}}}$ ${\displaystyle {\mathfrak {P}}}$ ${\displaystyle {\mathfrak {p}}{\mathcal {O}}_{E}}$ ${\displaystyle {\mathcal {O}}_{E}}$ ${\displaystyle E}$ ${\displaystyle G_{\mathfrak {P}}}$ ${\displaystyle {\mathfrak {P}}}$ ${\displaystyle K}$ ${\displaystyle \{\sigma \in G\mid \sigma ({\mathfrak {P}})={\mathfrak {P}}\}}$ ${\displaystyle G}$

${\displaystyle G_{\mathfrak {P}}\longrightarrow G(k_{\mathfrak {P}}/k_{\mathfrak {p}}),\;\sigma \longrightarrow {\overline {\sigma }},}$

from the decomposition group to the Galois group of the extension of finite residual fields and . Here is the body automorphism . The core of this surjective group homomorphism is called the inertia group of over and provides the canonical group isomorphism ${\displaystyle G_{\mathfrak {P}}}$ ${\displaystyle k_{\mathfrak {P}}/k_{\mathfrak {p}}}$ ${\displaystyle k_{\mathfrak {P}}:={\mathcal {O}}_{E}/{\mathfrak {P}}}$ ${\displaystyle k_{\mathfrak {p}}:={\mathcal {O}}_{K}/{\mathfrak {p}}}$ ${\displaystyle {\overline {\sigma }}}$ ${\displaystyle k_{\mathfrak {P}}\rightarrow k_{\mathfrak {P}},\;x\mapsto \sigma x\operatorname {mod} {\mathfrak {P}}}$ ${\displaystyle I_{\mathfrak {P}}\subseteq G_{\mathfrak {P}}}$ ${\displaystyle {\mathfrak {P}}}$ ${\displaystyle K}$

${\displaystyle G_{\mathfrak {P}}/I_{\mathfrak {P}}{\stackrel {\sim }{\longrightarrow }}G(k_{\mathfrak {P}}/k_{\mathfrak {p}})}$.

As a Galois group an extension of finite fields is cyclic and is made by Frobenius automorphism ${\displaystyle G(k_{\mathfrak {P}}/k_{\mathfrak {p}})}$

${\displaystyle k_{\mathfrak {P}}/k_{\mathfrak {p}}\longrightarrow k_{\mathfrak {P}}/k_{\mathfrak {p}},\;\alpha \mapsto \alpha ^{q_{\mathfrak {p}}},\;q_{\mathfrak {p}}:={\mathcal {N}}({\mathfrak {p}})=\#k_{\mathfrak {p}},}$

generated. Each of his archetypes in under the canonical group isomorphism creates the factor group and is called a Frobenius automorphism of over . If the inertia group is non-trivial, there are several such archetypes. If one restricts one to the fixed module , a subspace of , then a well-defined automorphism arises regardless of the choice of . Let it denote the dimension of the subspace and the -dimensional identity matrix . ${\displaystyle G_{\mathfrak {P}}}$ ${\displaystyle G_{\mathfrak {P}}/I_{\mathfrak {P}}}$ ${\displaystyle \phi _{\mathfrak {P}}}$ ${\displaystyle {\mathfrak {P}}}$ ${\displaystyle K}$ ${\displaystyle \phi _{\mathfrak {P}}}$ ${\displaystyle V^{I_{\mathfrak {P}}}:=\{v\in V\mid \forall \sigma \in I_{\mathfrak {P}}:\,\rho (\sigma )(v)=v\}}$ ${\displaystyle V}$ ${\displaystyle \phi _{\mathfrak {P}}}$ ${\displaystyle \phi _{\mathfrak {P}}:V^{I_{\mathfrak {P}}}\rightarrow V^{I_{\mathfrak {P}}}}$ ${\displaystyle d_{\mathfrak {P}}:=\operatorname {dim} V^{I_{\mathfrak {P}}}}$ ${\displaystyle V^{I_{\mathfrak {P}}}}$ ${\displaystyle E_{\mathfrak {P}}}$ ${\displaystyle d_{\mathfrak {P}}}$

The Artinian L-series to illustrate the Galois is now defined by ${\displaystyle (\rho ,V)}$ ${\displaystyle G=G(E/K)}$

${\displaystyle L(\rho ,s):=\prod _{0\neq {\mathfrak {p}}\subset {\mathcal {O}}_{K}}\operatorname {det} (1-\phi _{\mathfrak {P}}q_{\mathfrak {p}}^{-s};V^{I_{\mathfrak {P}}})^{-1}:=\prod _{0\neq {\mathfrak {p}}\subset {\mathcal {O}}_{K}}{\big (}\operatorname {det} (E_{\mathfrak {P}}-\phi _{\mathfrak {P}}X)|_{X=q_{\mathfrak {p}}^{-s}}{\big )}^{-1},}$

in which the product runs through all non-zero prime ideals of the whole ring of . The first product is the abbreviation of this definition, which is to be explained by the second product: The expression yields a polynomial of degree in . In comparison to the characteristic polynomial of , the order of the coefficients is reversed in this polynomial . The notation means that in should be inserted in the polynomial instead of . The individual Euler factors do not depend on the choice of the overlying prime ideal , since any other choice only leads to a conjugated Frobenius automorphism which does not change the polynomial . Artin's L-series are thus well-defined. They converge absolutely in the half-plane and evenly for each in . So they represent analytical (holomorphic) functions there . ${\displaystyle K}$ ${\displaystyle \operatorname {det} (E_{\mathfrak {P}}-\phi _{\mathfrak {P}}X)}$ ${\displaystyle d_{\mathfrak {P}}}$ ${\displaystyle \mathbb {C} [X]}$ ${\displaystyle \operatorname {det} (XE_{\mathfrak {P}}-\phi _{\mathfrak {P}})}$ ${\displaystyle \phi _{\mathfrak {P}}}$ ${\displaystyle |_{X=q_{\mathfrak {p}}^{-s}}}$ ${\displaystyle q_{\mathfrak {p}}^{-s}}$ ${\displaystyle X}$ ${\displaystyle \operatorname {det} (E_{\mathfrak {P}}-\phi _{\mathfrak {P}}X)}$ ${\displaystyle (\operatorname {det} (E_{\mathfrak {P}}-\phi _{\mathfrak {P}}X)|_{X=q_{\mathfrak {p}}^{-s}}{\big )}^{-1}}$ ${\displaystyle {\mathfrak {p}}}$ ${\displaystyle {\mathfrak {P}}}$ ${\displaystyle G}$ ${\displaystyle \operatorname {det} (E_{\mathfrak {P}}-\phi _{\mathfrak {P}}X)}$ ${\displaystyle \Re (s)>1}$ ${\displaystyle \delta >0}$ ${\displaystyle \Re (s)\geq 1+\delta }$

The character of a representation of the Galois group is defined as its function ${\displaystyle \rho :G\mapsto GL(V)}$ ${\displaystyle G}$

${\displaystyle \chi :=\chi _{\rho }:G\longrightarrow \mathbb {C} ,\sigma \longmapsto \operatorname {Spur} \rho (\sigma ).}$

Two representations and the Galois group are called equivalent if the modules and , i.e. the Abelian groups and , on which the operates as an automorphism group , are isomorphic. This is the case if and only if their characters and are the same. This is why the Artin L series is usually called . According to its definition it only runs through the finite places of , namely the non-zero prime ideals of . The gamma factor is still missing at the infinite places: ${\displaystyle (\rho ,V)}$ ${\displaystyle (\rho ',V')}$ ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle V}$ ${\displaystyle V'}$ ${\displaystyle V}$ ${\displaystyle V'}$ ${\displaystyle G}$ ${\displaystyle \chi _{\rho }}$ ${\displaystyle \chi _{\rho '}}$ ${\displaystyle L(\rho ,s)}$ ${\displaystyle L(\chi ,s)}$ ${\displaystyle K}$ ${\displaystyle {\mathcal {O}}_{K}}$

${\displaystyle \gamma (\chi ,s):=\prod _{{\mathfrak {p}}|\infty }L_{\mathfrak {p}}(\chi ,s),}$

in which

${\displaystyle L_{\mathfrak {p}}(\chi ,s)={\begin{cases}\Gamma _{\mathbb {R} }(s)^{\operatorname {dim} V^{G_{\mathfrak {P}}}}\cdot \Gamma _{\mathbb {R} }(s+1)^{\operatorname {dim} V/V^{G_{\mathfrak {P}}}}&{\text{falls}}\;{\mathfrak {p}}\;{\text{reell}}\\\Gamma _{\mathbb {C} }(s)^{\operatorname {dim} V}&{\text{falls}}\;{\mathfrak {p}}\;{\text{komplex}}\end{cases}}}$

with and as well as the decomposition group of about point situated . If and are real, it consists only of identity and is thus one element. If real, but complex, it has two elements: the identity and the unique element in , which swaps the two complex embeddings of in that belong to. ${\displaystyle \Gamma _{\mathbb {R} }(z):=\pi ^{-z/2}\Gamma (z/2)}$ ${\displaystyle \Gamma _{\mathbb {C} }(z):=2\cdot (2\pi )^{-z}\Gamma (z)}$ ${\displaystyle G_{\mathfrak {P}}}$ ${\displaystyle {\mathfrak {p}}}$ ${\displaystyle {\mathfrak {P}}}$ ${\displaystyle {\mathfrak {p}}}$ ${\displaystyle {\mathfrak {P}}}$ ${\displaystyle G_{\mathfrak {P}}}$ ${\displaystyle {\mathfrak {p}}}$ ${\displaystyle {\mathfrak {P}}}$ ${\displaystyle G_{\mathfrak {P}}}$ ${\displaystyle G}$ ${\displaystyle E}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle {\mathfrak {P}}}$

The Artin-leader of a character of a representation of is an ideal of which the branch of measures. With its help, the completed Artin L-function can now be defined by ${\displaystyle {\mathfrak {f}}(\chi )}$ ${\displaystyle \chi }$ ${\displaystyle \rho }$ ${\displaystyle G}$ ${\displaystyle K}$ ${\displaystyle \rho }$

${\displaystyle \Lambda (\chi ,s):=q(\chi )^{s/2}\cdot \gamma (\chi ,s)\cdot L(\chi ,s)=(|d_{K}|^{\operatorname {dim} V}{\mathcal {N}}{\mathfrak {f}}(\chi ))^{s/2}\prod _{{\mathfrak {p}}\mid \infty }L_{\mathfrak {p}}(\chi ,s)\cdot \prod _{{\mathfrak {p}}\not \mid \infty }(\operatorname {det} (1-\phi _{\mathfrak {P}}q_{\mathfrak {p}}^{-s};V^{I_{\mathfrak {P}}})^{-1}.}$

It is the leader of the L-function , which is a power of the magnitude of the discriminant of and the norm of the Artin guide of containing. This definition of the completed Artin L-function is initially only valid in the half-plane . but can be continued meromorphically to the whole complex number level. If one also denotes this continued L-function , then it fulfills the functional equation ${\displaystyle q(\chi ):=|d_{K}|^{\operatorname {dim} V}{\mathcal {N}}{\mathfrak {f}}(\chi )}$ ${\displaystyle \Lambda (\chi ,s)}$ ${\displaystyle d_{K}}$ ${\displaystyle K}$ ${\displaystyle \rho }$ ${\displaystyle \Re (s)>1}$ ${\displaystyle \Lambda (\chi ,s)}$ ${\displaystyle \Lambda }$

${\displaystyle \Lambda (\chi ,1-s)=\epsilon (\chi )\Lambda ({\overline {\chi }},s)}$

with a complex constant , which has the absolute value 1 and is called the Artin's root number of . The degree of is over or over . ${\displaystyle \epsilon (\chi )}$ ${\displaystyle \Lambda (\chi ,s)}$ ${\displaystyle \Lambda }$ ${\displaystyle \operatorname {dim} V}$ ${\displaystyle K}$ ${\displaystyle \operatorname {dim} V\cdot [K:\mathbb {Q} ]}$ ${\displaystyle \mathbb {Q} }$

The hitherto unproven Artin's conjecture states every Artinian L-function let analytically (holomorphic) of the half-plane to continue the character provided by from cutting into characters to irreducible representations of does not contain a trivial character. This assumption applies e.g. B. for one-dimensional representations, but is generally unproven. The existence of Artin's L-functions, which have poles in the critical strip , cannot be excluded so far. ${\displaystyle \Re (s)>1}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \chi }$ ${\displaystyle \rho }$ ${\displaystyle \rho }$ ${\displaystyle 0<\Re (s)<1}$

Artin's L-functions cannot only be defined in relation to representations of finite Galois extensions of algebraic number fields. More generally, global fields can be used as a basis, to which the algebraic number fields belong. In addition to the case of " algebraic number fields" there is also the case of " function field of a variable over a finite field with many elements." ${\displaystyle K=\;}$ ${\displaystyle K=\mathbb {F} _{p}(T)=\;}$ ${\displaystyle p\in \mathbb {P} }$

Assumed properties

One can read from known examples which properties a theory of the L-functions should have, and indeed it should

1. result in the position of the zero and pole points,
2. Provide functional equations with respect to the vertical lines Re ( s ) = constant,
3. result in special and interesting values ​​for integer arguments.

Detailed investigations have produced a large number of plausible guesses, for example about the exact type of the functional equations just given. Since the Riemann ζ-function is related to the Bernoulli numbers through its values ​​for even positive integers (and negative odd values) , it is obvious to look for a generalization of the Bernoulli numbers in the given theory. The fields of the p-adic numbers are used , which describe certain Galois modules .

The statistical properties of the zero distribution of the L-functions are of interest, among other things, because they are related to general problems, for example a hypothesis about the prime number distribution and other so-called generalized Riemannian hypotheses. The connection with the theories of random matrices and the so-called quantum chaos is also of interest. The fractal structure of the distributions was also examined using so-called scale analyzes. The self-similarity of the root distribution is very remarkable and is characterized by a large value of the fractal dimension , ~ 1.9. This very high value applies to more than 15 orders of magnitude of the zero point distribution of the Riemann ζ function and also to the zeros of other L functions.

See also

• Langlands program
• Birch and Swinnerton-Dyer conjecture

literature

• Tom M. Apostol : Introduction to Analytic Number Theory . Springer, New York 1976, ISBN 0-387-90163-9 .
• Peter Borwein , Stephen Choi, Brendan Rooney, Andrea Weirathmueller: The Riemann Hypothesis . Springer, New York 2008, ISBN 978-0-387-72125-5 .
• Daniel Bump et al .: An Introduction to the Langlands Program. Editors: Joseph Bernstein , Stephen Gelbart . Birkhäuser, Boston 2004, ISBN 3-7643-3211-5 .
• Henri Cohen : Advanced Topics in Computational Number Theory (= Graduate Texts in Mathematics. Volume 193). 1st edition. Springer-Verlag, New York 2000, ISBN 0-387-98727-4 . (In particular chapters 3 and 4 and section 10.3)
• Aleksandar Ivić : The Riemann Zeta-Function: theory and applications . Dover, Mineola 2003, ISBN 0-486-42813-3 .
• Henryk Iwaniec , Emmanuel Kowalski : Analytic Number Theory . American Mathematical Society , Providence 2004, ISBN 0-8218-3633-1 .
• Anatoly A. Karatsuba , SM Voronin : The Riemann Zeta-Function . Walter de Gruyter, Berlin 1992, ISBN 3-11-013170-6 .
• Jürgen Neukirch : Algebraic number theory. Springer-Verlag, Berlin / Heidelberg 1992, ISBN 3-540-54273-6 . (In particular Chapter VII)
• Alberto Perelli : An Introduction to the Selberg Class of L-Functions. Lecture script, Vilnius University, September 2007, Link .
• Cristian Popescu , Karl Rubin , Alice Silverberg (eds.): Arithmetic of L-functions (= IAS / Park City Mathematics Series. Volume 18). 1st edition. American Mathematical Society , Providence, Rhode Island, USA 2011, ISBN 978-0-8218-5320-7 .
• Jörn Steuding : Value-Distribution of L-Functions (= Lecture Notes in Mathematics. Volume 1877). 1st edition. Springer, Berlin, Heidelberg, New York 2007, ISBN 978-3-540-26526-9 .

Web links

• The L-functions and modular forms database - LMFDB Extensive collection of L-functions and other number-theoretic objects.
• Glimpses of a new (mathematical) world , Physorg.com , March 13, 2008
• Creeping Up on Riemann , Science News, April 2, 2008
• Hunting the elusive L-function
• K. Soundararajan : L-Functions . Lecture series, 2014.
• Analytic L-functions: Definitions, Theorems and Connections

Individual evidence

1. ^ Iwaniec, Kowalski: Analytic Number Theory. 2004, Chapter 5, Section 1, p. 94.
2. ^ Iwaniec, Kowalski: Analytic Number Theory. 2004, Chapter 5, Section 1, p. 95.
3. ^ Atle Selberg : Old and new conjectures and results about a class of Dirichlet series. In: Enrico Bombieri et al. (Ed.): Proceedings of the Amalfi Conference on Analytic Number Theory. 1992, pp. 367-385; Collected papers. Vol. II, Springer, 1991, pp. 47-63.
4. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 1, 1992, p. 439ff.
5. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 1, Sentence 1.1, 1992, p. 439.
6. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 1, Theorem 1.6, 1992, p. 445.
7. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 1, Theorem 1.6, 1992, p. 445.
8. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 1, Corollary 1.7, 1992, p. 446.
9. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 2, 1992, pp. 454f.
10. ↑ Tom M. Apostol : Note on the trivial zeros of Dirichlet L-functions. In: Proceedings of the American Mathematical Society. Volume 94, number 1, pp. 29-30. doi: 10.1090 / S0002-9939-1985-0781049-8
11. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 2, Sentence 2.1, 1992, p. 455.
12. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 2, Sentence 2.1, 1992, p. 455.
13. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 2, 1992, p. 457.
14. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 2, Theorem 2.8, 1992, p. 461.
15. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 2, Definition 2.5, 1992, p. 459.
16. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 2, Theorem 2.8, 1992, p. 461.
17. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 2, Sentence 2.6, 1992, p. 459, Theorem 2.8, p. 461.
18. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 2, 1992, p. 455.
19. ↑ PGL Dirichlet : Proof of the theorem that every unlimited arithmetic progression whose first term and difference are whole numbers without a common factor contains an infinite number of prime numbers. In: Abhand. Ak. Knowledge Berlin. (1837), pp. 45-81; Werke I (1889), pp. 313–342.
20. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 5, Sentence 5.14, 1992, p. 490.
21. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 5, Sentence 5.13, 1992, p. 490.
22. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 5, Definition 5.1, 1992, p. 478.
23. ^ Steuding: Value Distribution of L-Functions. 2007, Chapter 13, Section 1, p. 250.
24. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 5, Sentence 5.2, 1992, p. 478.
25. ^ Iwaniec, Kowalski: Analytic Number Theory. 2004, Chapter 5, Section 10, p. 125.
26. ^ Steuding: Value Distribution of L-Functions. 2007, Chapter 13, Section 1, p. 250.
27. ^ Iwaniec, Kowalski: Analytic Number Theory. 2004, Chapter 5, Section 10, p. 125.
28. ^ Iwaniec, Kowalski: Analytic Number Theory. 2004, Chapter 5, Section 10, p. 125.
29. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 5, Corollary 5.10, 1992, p. 487.
30. ^ Iwaniec, Kowalski: Analytic Number Theory. 2004, Chapter 5, Section 10, p. 125.
31. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 5, Corollary 5.10, 1992, p. 487.
32. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 5, 1992, p. 488.
33. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 5, Corollary 5.11, 1992, p. 488.
34. ↑ Neukirch: Algebraic Number Theory. 1992, Chapter 7, Paragraph 6, p. 491.
35. ↑ Neukirch: Algebraic Number Theory. 1992, Chapter 7, Paragraph 8, p. 515.
36. ↑ Neukirch: Algebraic Number Theory. 1992, Chapter 7, Paragraph 6, Definition 6.1, p. 492.
37. ↑ Neukirch: Algebraic Number Theory. 1992, Chapter 7, Paragraph 3, p. 464.
38. ↑ Neukirch: Algebraic Number Theory. 1992, Chapter 1, Paragraph 5, p. 31.
39. ^ Cohen: Advanced Topics in Computational Number Theory. 2000, Chapter 3, Section 3, p. 135.
40. ↑ Neukirch: Algebraic Number Theory. 1992, Chapter 7, Paragraph 6, p. 492.
41. ↑ Neukirch: Algebraic Number Theory. 1992, Chapter 7, Paragraph 6, p. 494.
42. ↑ Neukirch: Algebraic Number Theory. 1992, Chapter 7, paragraphs 6 to 8, pp. 491-525.
43. ↑ Popescu et al. (Ed.): Arithmetic of L-Functions. 2011, Part III, Lecture 2, p. 377.
44. ↑ Neukirch: Algebraic Number Theory. 1992, Chapter 7, Paragraph 8, Note 2, p. 525.
45. ↑ Popescu et al. (Ed.): Arithmetic of L-Functions. 2011, Part III, Lecture 2, p. 377.
46. ↑ Popescu et al. (Ed.): Arithmetic of L-Functions. 2011, Part III, Lecture 2, p. 378.
47. ↑ Popescu et al. (Ed.): Arithmetic of L-Functions. 2011, Part III, Lecture 2, pp. 378 and 379.
48. ↑ Popescu et al. (Ed.): Arithmetic of L-Functions. 2011, Part III, Lecture 2, p. 382.
49. ↑ Popescu et al. (Ed.): Arithmetic of L-Functions. 2011, Part III, Lecture 2, p. 379.
50. ↑ Popescu et al. (Ed.): Arithmetic of L-Functions. 2011, Part III, Lecture 2, p. 383.
51. ↑ Popescu et al. (Ed.): Arithmetic of L-Functions. 2011, Part III, Lecture 2, pp. 358, 383 and 384.
52. ↑ Popescu et al. (Ed.): Arithmetic of L-Functions. 2011, Part III, Lecture 2, p. 384, Section 3.2.
53. ^ Perelli: An Introduction to the Selberg Class of L-Functions. 2007, chap. 3, Invariants, p. 17.
54. ^ Perelli: An Introduction to the Selberg Class of L-Functions. 2007, chap. 2, Basic Theory of the Selberg Class, p. 7.
55. ↑ Popescu et al. (Ed.): Arithmetic of L-Functions. 2011, Part III, Lecture 2, p. 384, Theorem 2.1.
56. ↑ Popescu et al. (Ed.): Arithmetic of L-Functions. 2011, Part III, Lecture 2, p. 384, Section 3.2, with p. 361, Proposition 1.1.
57. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 10, Introduction, 1992, p. 539.
58. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 10, 1992, pp. 539 and 540.
59. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 10, Definition 10.1, 1992, p. 540.
60. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 10, 1992, p. 540.
61. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 10, 1992, p. 541.
62. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 10, 1992, p. 544.
63. ↑ Ehud de Shalit: Artin L Functions. In: An Introduction to the Langlands Program. Bernstein, Gelbart (Ed.), 2004, Chapter 4, Section 3.1, p. 75, and Section 4.1, p. 80.
64. ↑ Neukirch: Algebraic Number Theory. Chapter 7, Paragraph 12, 1992, pp. 558f.
65. ↑ Ehud de Shalit: Artin L Functions. In: An Introduction to the Langlands Program. Bernstein, Gelbart (Ed.), 2004, Chapter 4, Section 4.2, p. 80.
66. ↑ Ehud de Shalit: Artin L Functions. In: An Introduction to the Langlands Program. Bernstein, Gelbart (Ed.), 2004, Chapter 4, Section 4.3, Theorem 4.1, p. 81.
67. ^ Iwaniec, Kowalski: Analytic Number Theory. 2004, Chapter 4, Section 5.13, p. 141.
68. ↑ Ehud de Shalit: Artin L Functions. In: An Introduction to the Langlands Program. Bernstein, Gelbart (Ed.), 2004, Chapter 4, Conjecture 5.1, p. 83.
69. ^ Iwaniec, Kowalski: Analytic Number Theory. 2004, Chapter 5, Section 5.13, p. 142.
70. ↑ Ehud de Shalit: Artin L Functions. In: An Introduction to the Langlands Program. Bernstein, Gelbart (Ed.), 2004, Chapter 4, Section 3.1, p. 75.
71. ^ O. Shanker: Random matrices, generalized zeta functions and self-similarity of zero distributions . In: J. Phys. A: Math. Gen. tape 39 , 2006, p. 13983-13997 , doi : 10.1088 / 0305-4470 / 39/45/008 .

Remarks

1. ↑ The Ramanujan conjecture relates to the coefficients of the Dirichlet series. It says, for any is . Whereby the maximum implicit constant in the Landau symbol of depend. ${\displaystyle \textstyle \lambda (f,n)}$ ${\displaystyle \textstyle \epsilon >0}$ ${\displaystyle \textstyle \lambda (f,n)=O(n^{\epsilon })}$ ${\displaystyle \textstyle O}$ ${\displaystyle \textstyle \epsilon }$
2. ↑ Explanation of the terms "digit" and "complete envelope": the digits of are, apart from the equivalence of the absolute amounts, the usual absolute amount and the p-adic absolute amounts , whereby the exponent of the prime number is designated and set in the prime factorization of . The corresponding complete hulls are the real numbers and the p-adic fields . ${\displaystyle \mathbb {Q} }$ ${\displaystyle |\cdot |_{\infty }:=|\cdot |:\mathbb {Q} \rightarrow \mathbb {R} _{\geq 0}}$ ${\displaystyle |\cdot |_{p}:\mathbb {Q} \rightarrow \mathbb {R} _{\geq 0},|x|_{p}:=p^{-e_{p}(x)}}$ ${\displaystyle e_{p}(x)\in \mathbb {Z} }$ ${\displaystyle p}$ ${\displaystyle x\neq 0}$ ${\displaystyle |0|_{p}:=0}$ ${\displaystyle \mathbb {Q} _{\infty }:=\mathbb {R} }$ ${\displaystyle \mathbb {Q} _{p}}$