Block plan
A block plan (also block design or combinatorial design ) is a finite incidence structure that is particularly important in finite geometry , combinatorics and statistical experiment planning . Block plans are a common generalization of the finite affine planes and the finite projective planes .
Important methods for the characterization of block plans and for the construction of new block plans from known ones are the resolution and the tactical breakdown of a block plan. The resolution generalizes the concept of the parallelism of a block diagram , as described in this article, and is itself a special case of tactical decomposition .
Definitions and spellings
Let be a finite incidence structure where the elements of are called points and the elements of are called blocks . Furthermore, are natural numbers , then the incidence structure is as referred -Blockplan if the following axioms hold:
- (B1) has exactly points, so ,
- (B2) every block of incised with exactly points, so ,
- (B3) for every point set with different points there are exactly different blocks, which each incise with all points of, i.e. and
- (B4) , that is, is a non-degenerate or true incidence structure.
An alternative designation for a block plan is also used. In the case of , one also simply writes and speaks of a Steiner system (after Jakob Steiner ). A block plan ( ) is also known as a Steiner-Triple system . Sometimes a block design is also written as, the additional parameter is explained below.
A block plan is often referred to for short as a block plan and a block plan is simply referred to as a block plan, since it is the most commonly used case.
The constant number of all blocks of through a point of is denoted by and the number of all blocks of by .
Based on certain geometric models for a block plan, its blocks are sometimes referred to as straight lines , circles , planes or the like. If a point is incised with a block , then the following ways of speaking are also common: lies on or goes through . If a point intersects with several blocks, it is also said that the blocks intersect .
Block plans in which a block is incised with all points, or in which the -element subsets of the point set correspond exactly to the blocks, are referred to as trivial block plans.
A block must be formally differentiated from the set of points incising with it , but in practice it is usually possible to identify a block with its set of points and to interpret the incidence relation as a set-theoretical inclusion. Such block plans are also referred to as simple (see the examples in the article “Incidence structure”).
properties
The following applies to the number of blocks in a block plan:
- .
With for it is the number of blocks with all the points of any set of points with incise points, ie , applies to this:
- .
A block diagram with given parameters can only exist if these are integers. This is called the divisibility conditions for the existence of block plans.
For block plans results from the two formulas taking into account :
- .
In addition, the Fisher inequality applies to the block plans :
- .
In addition to the finite, projective and affine spaces mentioned below in the examples, block plans are interrelated to many other structures of combinatorics. For example, the existence of a block diagram with is equivalent to the existence of a Hadamard matrix of order . For this reason, such block plans are also known as Hadamard block plans . The Assmus-Mattson theorem describes the relationship between codes and block plans .
A central question in the theory of block plans is for which values of the parameter a block plan exists at all. A groundbreaking result by Peter Keevash (2014) shows that the divisibility conditions for existence are sufficient if the number of points is large enough.
There are also a number of necessary criteria for the existence of certain block plans, which can be used to exclude many parameter combinations. Such criteria are provided, for example, by the generalized Fisher inequality (also called the Ray-Chaudhuri-Wilson theorem ) and the Bruck-Ryser-Chowla theorem .
Symmetrical block plans
A block diagram that has as many blocks as there are points is called symmetric or projective . Symmetrical block plans can be characterized by different, equivalent statements among the 2-block plans: Let a -Block plan, be the total number of its blocks and be an incidence matrix of this block plan. Then the following statements are equivalent:
- The number of points equals the number of the blocks and thus applies , that is, is symmetrical. It applies
- The number of blocks that any point will incise is equal to the number of points that any block will incise .
- here is the - identity matrix , the - one matrix
- Here is the -Einheitsmatrix, the -Einsmatrix
- Two different blocks each intersect at exactly points.
- Every two different blocks have a constant, positive number of points in common, that is, they meet the regularity condition . See regularity conditions and types of finite incidence structures .
- has the type as the incidence structure , that is, satisfies the regularity conditions .
The interval in which the number of dots (or blocks) with respect to the order of a symmetrical varies -Blockplans, is obtained as if a non-trivial block diagram with present. The lower extreme case is given for Hadamard block plans and the upper extreme case for the finite projective planes .
Parallelisms and affine block plans
A parallelism of a block plan is an equivalence relation on the set of blocks for which the Euclidean parallel postulate applies:
- For every block and every point there is exactly one block which is too parallel and which is incident to it.
Blocks are referred to as parallel (notation ) if they are in the same equivalence class. The equivalence classes themselves are also referred to as parallel classes or parallel sets. For two parallel blocks it applies that they (more precisely: the point sets that are incised with them) are either identical or disjoint:
- .
A parallelism of a block plan, in which any two non-parallel blocks always have the same number of points in common, is called affine and the associated block plan is called an affine block plan . While in general a block diagram can allow several parallelisms, in an affine block diagram the parallelism is uniquely determined and the reverse of the above relationship also applies:
- .
For block diagrams with parallelisms, Bose's theorem applies , which in this case represents a tightening of Fisher's inequality.
Examples
The Witt block plans (in the narrow sense) are easy 5-block designs, their derivatives, which are often referred to as block Witt plans to provide examples of nontrivial simple 4- and 3-block designs.
Affine geometries as block plans
The affine space of the dimension over the finite body with elements is noted as. It becomes a block diagram by using the point set of affine space as the set of points and the -dimensional affine subspaces as blocks. More precisely, it is a block plan. The usual parallelism of affine geometry is a parallelism for the block plan and the block plan thus becomes an affine block plan if and only if it applies, that is, the blocks are hyperplanes of space. The parameters of the block plan are:
- .
Here stands for the Gaussian binomial coefficient given by the formula
for can be calculated. The rooms are even for 3 block plans with . An affine block plan is special with its geometric parallelism .
Projective geometries as block plans
The projective space of the dimension over the finite body is noted as. The block plan has the set of projective points as the set of points and the set of -dimensional projective subspaces of the . This is a block diagram with the parameters
- .
In the case so if the blocks are the hyperplanes of the room, the block diagram is symmetrical.
Illustrative examples
As special cases of the above-mentioned classical geometric spaces, one can understand a finite projective plane of order as a block plan and a finite affine plane of order as a block plan. The points on the level correspond to the points on the block plan and the straight lines on the level correspond to the blocks in the block plan. However, the existence of the corresponding level of order is assumed and this is not the case for all .
Small levels, see also the illustrations at the end of the section:
- The projective level of order 2 (the Fano level ) is a symmetrical block plan at the same time it is "the" smallest Hadamard block plan.
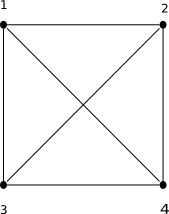
- The affine levels of order 2 and 3 and with their usual and only possible parallelism form an affine block plan or block plan.
| 7 pts, 7 blocks of 3 pts each | 4 pts, 6 blocks with 2 pts each | 9 pts, 12 blocks of 3 pts each |
Further (counter) examples of simple block plans
Non-existent simple 2-block plans
There are no simple block diagrams for the parameter triples (in the area ) that appear in the following list , although the usual parameter conditions are met:
Existing simple t-block plans with t ≥ 4
For a long time, concrete examples of simple block plans were only known sporadically.
Something like this:
- and
- and
- and
- and
- and
- and
Until the 1980s, it was even unclear whether (for example) simple block plans even existed. Then gradually several examples were found:
- and
- and
- and
- and
- and
In recent years, with the help of further refined group-theoretical , geometric and computer-aided methods, a number of simple block plans have even been found; u. a. :
- and
- and
Application in statistical design of experiments
For example, let's say skin cancer researchers want to test three different sunscreens. To do this, they apply two different sun creams to the top of the hands of each subject. After exposure to UV light, they note the skin irritation in the form of sunburn. The number of treatments is 3 (sunscreens) and the block size is 2 (hands per person).
A suitable balanced, incomplete test plan can be generated in R with the design.bib function from the R package agricolae and is shown in the following table:
| Plots | block | Treatment |
|---|---|---|
| 101 | 1 | 3 |
| 102 | 1 | 1 |
| 201 | 2 | 1 |
| 202 | 2 | 2 |
| 301 | 3 | 3 |
| 302 | 3 | 2 |
| 401 | 4th | 3 |
| 402 | 4th | 1 |
| 501 | 5 | 2 |
| 502 | 5 | 3 |
| 601 | 6th | 1 |
| 602 | 6th | 2 |
The researchers select the parameters and for the block diagram, which are then entered into the R function. Then the remaining parameters and are determined automatically.
With the designations to for the blocks one obtains the following incidence matrix :
| treatment | Block A | Block B | Block C | Block D | Blocks | Block F |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| 2 | 0 | 1 | 1 | 0 | 1 | 1 |
| 3 | 1 | 0 | 1 | 1 | 1 | 0 |
Each treatment comes in four blocks, so is .
Two blocks ( and ) simultaneously contain the treatments and and the same applies to the treatment pairs and . So is .
In this example it is impossible to get a complete test plan (all treatments in each block) because three sunscreens are tested, but only two hands are available per person.
literature
- Thomas Beth , Dieter Jungnickel , Hanfried Lenz : Design Theory . 2nd Edition. BI Wissenschaftsverlag, London / New York / New Rochelle / Melbourne / Sidney 1999, ISBN 0-521-33334-2 (first edition: 1986).
- Albrecht Beutelspacher : Introduction to Finite Geometry . I. Block plans. BI Wissenschaftsverlag, Mannheim / Vienna / Zurich 1982, ISBN 3-411-01632-9 .
- Daniel R. Hughes, Fred C. Piper: Design Theory . Cambridge University Press, Cambridge (et al.) 1985, ISBN 0-521-25754-9 .
- Jacobus Hendricus Van Lint , Richard Michael Wilson : A Course in Combinatorics . Cambridge University Press, 1992, ISBN 0-521-42260-4 , pp. 188 .
- Kenneth H. Rosen (Ed.): Handbook of Discrete and Combinatorial Mathematics . CRC Press, 2000, ISBN 0-8493-0149-1 .
- Tosiro Tsuzuku: Finite Groups and Finite Geometries (= Cambridge Tracts in Mathematics . Volume 78 ). Cambridge University Press, Cambridge (et al.) 1982, ISBN 0-521-22242-7 .
Web links
- Eric W. Weisstein : block design . In: MathWorld (English).
- Script Algebraic Structures and Discrete Mathematics . (PDF; 1.01 MB) p. 67
- block design in the Encyclopaedia of Mathematics
- Publications from the University of Bayreuth
- Charles Colbourn , Jeff Dinitz : Handbook of Combinatorial Designs
References and comments
- ↑ Beutelspacher (1982)
- ↑ The additional parameter names given in brackets are those generally used for the parameters of a finite incidence structure .
- ↑ Beth, Jungnickel, Lenz (1986, 1999), definition I.3.1
- ↑ Beth, Jungnickel, Lenz (1986, 1999), Corollary I.8.6
- ^ Peter Keevash: The existence of designs . arXive. 2014.
- ↑ A Design Dilemma Solved, Minus Designs . Quanta Magazine. June 9, 2015. Accessed June 27, 2015.
- ↑ Gil Kalai: Designs exist! . Séminaire BOURBAKI.
- ↑ Timothy Gowers : PROBABILISTIC COMBINATORICS AND THE RECENT WORK OF PETER KEEVASH . BULLETIN (New Series) OF THE AMERICAN MATHEMATICAL SOCIETY, Volume 54, No. 1, January 2017, pp. 107–116, http://dx.doi.org/10.1090/bull/1553
- ↑ Beutelspacher 1.4.4.
- ↑ Kenneth H. Rosen (Ed.): Handbook of Discrete and Combinatorial Mathematics . CRC Press, 2000, ISBN 0-8493-0149-1 , pp. 771 .
- ↑ Tosiro Tsuzuku: Finite Groups and Finite Geometries (= Cambridge Tracts in Mathematics . Volume 78 ). Cambridge University Press, Cambridge (et al.) 1982, ISBN 0-521-22242-7 , pp. 62 .
- ↑ a b c Beth, Jungnickel, Lenz (1986, 1999), I. Examples and basic definitions
- ↑ In the case of symmetrical block plans, the parameter usually refers to the block plan order . The number of dimensions mentioned here is generally not identical to the block plan order.
- ↑ Rosen et al .: Handbook ... p. 764.773 .
- ↑ So the projective level of order 6 does not exist either .
- ↑ So the projective level of order 10 does not exist either .
- ↑ a b Kenneth H. Rosen (Ed.): Handbook of Discrete and Combinatorial Mathematics . CRC Press, 2000, ISBN 0-8493-0149-1 , pp. 767 .
- ^ Daniel R. Hughes, Fred C. Piper: Design Theory . Cambridge University Press, Cambridge (et al.) 1985, ISBN 0-521-25754-9 , pp. 144 ff .
- ^ Daniel R. Hughes, Fred C. Piper: Design Theory . Cambridge University Press, Cambridge (et al.) 1985, ISBN 0-521-25754-9 , pp. 148, 152 .
- ↑ See web link to the publications of the University of Bayreuth.
- ↑ Felipe de Mendiburu: agricolae: Statistical Procedures for Agricultural Research. June 12, 2016. Retrieved February 19, 2017 .
















































































![\ textstyle \ left [{n \ atop i} \ right] _ {q}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04bfae3da222bea79b0bde4564662cc24a3eae6a)