Incidence matrix

This article covers the incidence matrix of graphs . A more general view is described in the article on incidence structures .

An incidence matrix of a graph is a matrix that stores the relationships between the nodes and edges of the graph. If the graph has nodes and edges, its incidence matrix is ​​a matrix. The entry in the -th row and -th column indicates whether the -th node is part of the -th edge. If there is a 1 here, there is an incidence relationship ; if there is a 0, there is no incidence. It is assumed that the nodes are numbered from 1 to and the edges are numbered from 1 to . ${\displaystyle n}$ ${\displaystyle m}$ ${\displaystyle n\times m}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle n}$ ${\displaystyle m}$

definition

Undirected graph

For a loop-free undirected graph with and the incidence matrix is formally defined by: ${\displaystyle G=(V,E)}$ ${\displaystyle V=\{v_{1},\dotsc ,v_{n}\}}$ ${\displaystyle E=\{e_{1},\dotsc ,e_{m}\}}$ ${\displaystyle B=(b_{i,j})}$

${\displaystyle b_{ij}:={\begin{cases}1,&{\text{ falls }}v_{i}\in e_{j}\\0,&{\text{ sonst}}\end{cases}}}$

The incidence matrix of an undirected graph therefore contains exactly 2 entries different from 0 in each column.

Directed graph

For a loop-free directed graph with and the incidence matrix is defined by: ${\displaystyle G=(V,E)}$ ${\displaystyle V=\{v_{1},\dotsc ,v_{n}\}}$ ${\displaystyle E=\{e_{1},\dotsc ,e_{m}\}}$ ${\displaystyle B=(b_{i,j})}$

${\displaystyle b_{ij}:={\begin{cases}1,&{\text{ falls }}e_{j}=(v_{i},x)\\0,&{\text{ falls }}v_{i}\notin e_{j}\\-1,&{\text{ falls }}e_{j}=(x,v_{i})\end{cases}}}$

where here represents any node. ${\displaystyle x}$

The incidence matrix of a directed graph therefore contains exactly once the (start node) and once the (end node) in each column . Alternatively, incidence matrices are sometimes defined with the opposite sign, that is, if the edge begins at the node and if the edge ends at the node . This is particularly important to consider when considering inequalities that contain incidence matrices. ${\displaystyle 1}$ ${\displaystyle -1}$ ${\displaystyle b_{ij}=-1}$ ${\displaystyle e_{j}}$ ${\displaystyle v_{i}}$ ${\displaystyle b_{ij}=1}$ ${\displaystyle e_{j}}$ ${\displaystyle v_{i}}$

Examples

Undirected graph

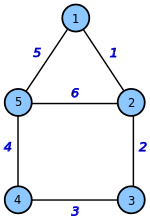
As an example, we will now examine the graph on the right , which resembles the house of Nicholas , with the numbering of the nodes and edges indicated in the picture . To create an incidence matrix from this graph, we start with an empty matrix. This contains columns and rows for the graph under consideration . The edges are entered in the columns and the corners in the rows. ${\displaystyle j=6}$ ${\displaystyle i=5}$

The numbers on the edges are not to be confused with the weightings of the edges. They describe the names of the edges that can be found in the matrix as columns. ${\displaystyle (e_{1},e_{2},\dotsc ,e_{6})}$

Now the associated nodes are marked with 1 for each column (edge), all other nodes with 0. The following incidence matrix results:

${\displaystyle {\begin{pmatrix}1&0&0&0&1&0\\1&1&0&0&0&1\\0&1&1&0&0&0\\0&0&1&1&0&0\\0&0&0&1&1&1\\\end{pmatrix}}}$

or formatted as a table:

	e 1	e 2	e 3	e 4	e 5	e 6
v 1	1	0	0	0	1	0
v 2	1	1	0	0	0	1
v 3	0	1	1	0	0	0
v 4	0	0	1	1	0	0
v 5	0	0	0	1	1	1

If the incidence matrix of an undirected graph is constructed correctly, then each column (edge) must have a total of 2, since each edge connects exactly 2 points. If a point is connected to itself, there is a 2 in the corresponding cell. The sum of each row corresponds to the edges that lead to the corresponding point.

Directed graph

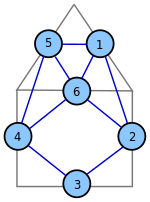
As an example, an incidence matrix of a directed graph , we now consider the rightmost graphs . Again we assume the numbering of the nodes as given. The edges are numbered as follows: It is and . So the incidence matrix is ​​a matrix: ${\displaystyle e_{1}=(1,2),e_{2}=(3,2),e_{3}=(3,1),e_{4}=(1,4),e_{5}=(2,4),e_{6}=(4,3).}$ ${\displaystyle |E|=6=m}$ ${\displaystyle |V|=4=n}$ ${\displaystyle 4\times 6}$

${\displaystyle {\begin{pmatrix}1&0&-1&1&0&0\\-1&-1&0&0&1&0\\0&1&1&0&0&-1\\0&0&0&-1&-1&1\\\end{pmatrix}}}$

or formatted as a table:

	e 1	e 2	e 3	e 4	e 5	e 6
v 1	1	0	−1	1	0	0
v 2	−1	−1	0	0	1	0
v 3	0	1	1	0	0	−1
v 4	0	0	0	−1	−1	1

The incidence matrix of a directed graph is correctly constructed if there are two non-zero entries in each column that add up to zero.

Relation to other matrices

Another matrix that describes graphs is the Laplace matrix . It's a matrix, where is the number of nodes . The coefficients of their diagonal contain the degree of the nodes of the graph, and the other coefficients in row and in column are equal to −1 if the nodes and are connected and 0 if they are not. ${\displaystyle n\times n}$ ${\displaystyle n}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle i}$ ${\displaystyle j}$

If the incidence matrix is ​​a directed graph , we can compute the Laplacian matrix by multiplying by its transposed matrix : ${\displaystyle B(G)}$ ${\displaystyle G}$ ${\displaystyle L(G)}$ ${\displaystyle B(G)}$ ${\displaystyle B^{\mathrm {T} }(G)}$

${\displaystyle L(G)=B(G)\cdot B^{\mathrm {T} }(G)}$

For example for the directed graph in the adjacent figure:

${\displaystyle L(G)={\begin{pmatrix}-1&0&0&0&1&0\\1&-1&0&0&0&1\\0&1&-1&0&0&0\\0&0&1&-1&0&0\\0&0&0&1&-1&-1\\\end{pmatrix}}\cdot {\begin{pmatrix}-1&1&0&0&0\\0&-1&1&0&0\\0&0&-1&1&0\\0&0&0&-1&1\\1&0&0&0&-1\\0&1&0&0&-1\\\end{pmatrix}}={\begin{pmatrix}2&-1&0&0&-1\\-1&3&-1&0&-1\\0&-1&2&-1&0\\0&0&-1&2&-1\\-1&-1&0&-1&3\\\end{pmatrix}}}$

The adjacency matrix of a graph is another matrix that describes the graph . It's a matrix, where is the number of nodes . The other coefficients in row and in column are equal to 1 if the nodes and are connected and 0 otherwise. For an undirected graph this matrix is ​​symmetric. ${\displaystyle n\times n}$ ${\displaystyle n}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle i}$ ${\displaystyle j}$

The degree matrix of a graph is a - diagonal matrix that lists the degree of each node. The coefficient in the row and in the column indicates the degree of the node , all other coefficients are 0. ${\displaystyle n\times n}$ ${\displaystyle i}$ ${\displaystyle i}$ ${\displaystyle i}$

If the incidence matrix of an undirected graph is its adjacency matrix and its degree matrix, then: ${\displaystyle B(G)}$ ${\displaystyle G}$ ${\displaystyle A(G)}$ ${\displaystyle D(G)}$

${\displaystyle A(G)+D(G)=B(G)\cdot B^{\mathrm {T} }(G)}$

For example for the undirected graph in the adjacent figure:

${\displaystyle A(G)+D(G)={\begin{pmatrix}1&0&0&0&1&0\\1&1&0&0&0&1\\0&1&1&0&0&0\\0&0&1&1&0&0\\0&0&0&1&1&1\\\end{pmatrix}}\cdot {\begin{pmatrix}1&1&0&0&0\\0&1&1&0&0\\0&0&1&1&0\\0&0&0&1&1\\1&0&0&0&1\\0&1&0&0&1\\\end{pmatrix}}={\begin{pmatrix}2&1&0&0&1\\1&3&1&0&1\\0&1&2&1&0\\0&0&1&2&1\\1&1&0&1&3\\\end{pmatrix}}}$

By isolating the diagonal from the other values, we get:

${\displaystyle A(G)={\begin{pmatrix}0&1&0&0&1\\1&0&1&0&1\\0&1&0&1&0\\0&0&1&0&1\\1&1&0&1&0\\\end{pmatrix}},\quad D(G)={\begin{pmatrix}2&0&0&0&0\\0&3&0&0&0\\0&0&2&0&0\\0&0&0&2&0\\0&0&0&0&3\\\end{pmatrix}}}$

The edge graph of an undirected graph is obtained by replacing its edges with nodes and connecting the new nodes if the corresponding original edges have a node in common. The figure opposite shows the edge graph of the undirected graph from the previous example.

If the incidence matrix of an undirected graph and the identity matrix , we can use the adjacency matrix of its line graph calculated as follows: ${\displaystyle B(G)}$ ${\displaystyle G}$ ${\displaystyle I_{m}}$ ${\displaystyle A(L(G))}$

${\displaystyle A(L(G))=B(G)\cdot B^{\mathrm {T} }(G)-2\cdot I_{m}}$

For example for the edge graph in the adjacent figure:

${\displaystyle A(L(G))={\begin{pmatrix}1&1&0&0&0\\0&1&1&0&0\\0&0&1&1&0\\0&0&0&1&1\\1&0&0&0&1\\0&1&0&0&1\\\end{pmatrix}}\cdot {\begin{pmatrix}1&0&0&0&1&0\\1&1&0&0&0&1\\0&1&1&0&0&0\\0&0&1&1&0&0\\0&0&0&1&1&1\\\end{pmatrix}}-{\begin{pmatrix}2&0&0&0&0&0\\0&2&0&0&0&0\\0&0&2&0&0&0\\0&0&0&2&0&0\\0&0&0&0&2&0\\0&0&0&0&0&2\\\end{pmatrix}}={\begin{pmatrix}0&1&0&0&1&1\\1&0&1&0&0&1\\0&1&0&1&0&0\\0&0&1&0&1&1\\1&0&0&1&0&1\\1&1&0&1&1&0\\\end{pmatrix}}}$

use

Storage of graphs in the computer

Incidence matrices are used in computer science to store graphs . The incidence matrix of a graph with nodes and edges requires a storage space of . Since the space complexity of adjacency matrices is, incidence matrices are more efficient in terms of storage space if there are fewer edges than nodes. ${\displaystyle n}$ ${\displaystyle m}$ ${\displaystyle {\mathcal {O}}(n\cdot m)}$ ${\displaystyle {\mathcal {O}}(n^{2})}$

Spectral graph theory

Furthermore, incidence matrices are used in spectral graph theory , where an attempt is made to draw conclusions about the properties of the represented graph based on certain properties of the incidence matrix .

optimization

The incidence matrix of an undirected bipartite graph is a totally unimodular matrix , just like that of a digraph . Therefore, under certain conditions, the integer solution of a linear optimization problem can be shown if the admissible set is defined by one of the incidence matrices mentioned above. In particular, this establishes a connection between discrete optimization and linear optimization .

literature

• Peter Knabner , Wolf Barth : Lineare Algebra. Basics and applications (=  Springer textbook ). Springer Spectrum, Berlin et al. 2013, ISBN 978-3-642-32185-6 .
• Reinhard Diestel : graph theory . 4th edition. Springer, Heidelberg et al. 2010, ISBN 978-3-642-14911-5 .

Individual evidence

1. ^ Manfred Brill: Mathematics for computer scientists. Introduction to practical examples from the world of computers . 2nd, completely revised edition. Hanser Fachbuchverlag, Munich et al. 2005, ISBN 3-446-22802-0 , p. 161-169 .