Laplace matrix

In graph theory, the Laplace matrix is a matrix that describes the relationships between the nodes and edges of a graph. Among other things, it is used to calculate the number of spanning trees and to estimate the expansiveness of regular graphs. It is a discrete version of the Laplace operator .

Laplace matrices and in particular their eigenvectors belonging to small eigenvalues are used in spectral clustering , a method of cluster analysis .

definition

The Laplace matrix of a graph with the set of nodes and the set of edges is a matrix. It is defined as , where denotes the degree matrix and the adjacency matrix of the graph. So the node and corresponding entry is ${\displaystyle L}$ ${\displaystyle V}$ ${\displaystyle E}$ ${\displaystyle |V|\times |V|}$ ${\displaystyle L:=D-A}$ ${\displaystyle D}$ ${\displaystyle A}$ ${\displaystyle v_{i}}$ ${\displaystyle v_{j}}$

${\displaystyle L_{i,j}:={\begin{cases}\deg(v_{i})&{\mbox{falls}}\ i=j\\-1&{\mbox{falls}}\ i\neq j\ {\mbox{und}}\ v_{i}{\mbox{ adjazent zu }}v_{j}\\0&{\mbox{sonst}}\end{cases}}}$

In particular, the Laplace matrix is ​​a - regular graph ${\displaystyle d}$

${\displaystyle L=d\cdot I-A}$

with the identity matrix . ${\displaystyle I}$

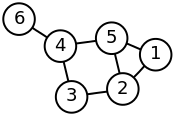
example

Numbering of the corners	Degree matrix	Adjacency matrix	Laplace matrix
	${\displaystyle \left({\begin{array}{rrrrrr}2&0&0&0&0&0\\0&3&0&0&0&0\\0&0&2&0&0&0\\0&0&0&3&0&0\\0&0&0&0&3&0\\0&0&0&0&0&1\\\end{array}}\right)}$	${\displaystyle \left({\begin{array}{rrrrrr}0&1&0&0&1&0\\1&0&1&0&1&0\\0&1&0&1&0&0\\0&0&1&0&1&1\\1&1&0&1&0&0\\0&0&0&1&0&0\\\end{array}}\right)}$	${\displaystyle \left({\begin{array}{rrrrrr}2&-1&0&0&-1&0\\-1&3&-1&0&-1&0\\0&-1&2&-1&0&0\\0&0&-1&3&-1&-1\\-1&-1&0&-1&3&0\\0&0&0&-1&0&1\\\end{array}}\right)}$

Relation to incidence matrix

The Laplace matrix can also be calculated from the incidence matrix . Let be an incidence matrix, then the Laplace matrix is ​​given by ${\displaystyle B}$ ${\displaystyle |E|\times |V|}$

${\displaystyle L=B^{\top }B}$

properties

We denote the eigenvalues ​​of the Laplace matrix, see spectrum (graph theory) . ${\displaystyle \lambda _{0}\leq \lambda _{1}\leq \cdots \leq \lambda _{n-1}}$

• ${\displaystyle L}$is symmetrical .
• ${\displaystyle L}$is positive-semidefinite , especially for everyone . ${\displaystyle \lambda _{i}\geq 0}$ ${\displaystyle i}$
• ${\displaystyle L}$is an M-matrix .
• The column and row totals are zero. In particular, is with eigenvector . ${\displaystyle \lambda _{0}=0}$ ${\displaystyle \mathbf {v} _{0}=(1,1,\dots ,1)}$
• The multiplicity of the eigenvalue is the number of connected components of the graph. ${\displaystyle 0}$