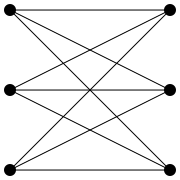
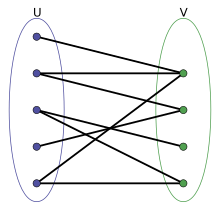
Bipartite graph

K _3,3 : completely bipartite graph with 3 nodes per subset

A simple, incomplete, bipartite graph with partition classes and ${\displaystyle U}$ ${\displaystyle V}$

A bipartite or paired graph is a mathematical model for relationships between the elements of two sets. It is very useful for investigating mapping problems . Furthermore, many graph properties can be calculated for bipartite graphs with significantly less effort than is possible in the general case.

Definitions

A simple graph is called bipartite or pair if its vertices can be divided into two disjoint subsets A and B , so that no edges run between the vertices within both subsets . This means that either and or and applies to each edge . The set is then referred to as the bipartition of the graph and the sets as partition classes . Put simply, a bipartite graph is a graph in which there are two groups of nodes within which no nodes are connected to each other. ${\displaystyle G=(V,E)}$ ${\displaystyle \{v,w\}\in E}$ ${\displaystyle v\in A}$ ${\displaystyle w\in B}$ ${\displaystyle v\in B}$ ${\displaystyle w\in A}$ ${\displaystyle \{A,B\}}$ ${\displaystyle G}$ ${\displaystyle A,B}$

The graph is called fully bipartite if there is a bipartition such that every node in is connected to every node in . Such a graph is also called , where and are the number of nodes of and . A fully bipartite graph that has or is called a star graph . ${\displaystyle G}$ ${\displaystyle \{A,B\}}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle K_{m,n}}$ ${\displaystyle m}$ ${\displaystyle n}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle m=1}$ ${\displaystyle n=1}$

properties

For all bipartite graphs:

• The pairing number corresponds to the node coverage number .
• The partition classes are, by definition, stable sets . ${\displaystyle A,B}$
• The chromatic index corresponds to its maximum degree . A valid edge coloring can be determined in. ${\displaystyle O(n\cdot m)}$
• Every bipartite graph can be colored by two nodes . Each partition class is therefore assigned a color. Conversely, every 2-colorable graph is also bipartite.
• A - regular bipartite graph has disjoint perfect matchings . ${\textstyle k}$ ${\textstyle k}$
• A graph is bipartite if and only if it does not contain a cycle of odd length.
• The edge chromatic number corresponds to its maximum degree .
• The list chromatic index is the same as the chromatic index . This means that bipartite graphs are a class of graphs for which the list coloring presumption applies.
• The following applies , where is the total chromatic number and the maximum degree . For bipartite graphs the total color conjecture applies . ${\displaystyle \chi _{T}(G)\leq \Delta (G)+2}$ ${\displaystyle \chi _{T}(G)}$ ${\displaystyle \Delta (G)}$
• All bipartite graphs are perfect graphs , so for each induced subgraph the clique number agrees with the chromatic number .

According to König's theorem , in bipartite graphs, the size of the minimum node coverage corresponds to the size of the maximum matching . An alternative and equivalent form of this theorem is that the size of the maximum independent set plus the size of the maximum matching equals the number of nodes. In any graph without isolated nodes , the size of the minimum edge coverage plus the size of a maximum matching corresponds to the number of nodes. Combining this equation with König's theorem, it follows that in bipartite graphs the size of the minimum edge coverage is equal to the size of the maximum independent set and that the size of the minimum edge coverage plus the size of the minimum node coverage is equal to the number of nodes.

In addition, every bipartite graph, the complement of every bipartite graph, the edge graph of every bipartite graph, and the complement of the edge graph of every bipartite graph are all perfect graphs . This was one of the results that motivated the definition of perfect graphs.

According to the theorem of strong perfect graphs, perfect graphs have a forbidden characterization that is similar to that of bipartite graphs: A graph is bipartite if and only if it has no odd cycle as a subgraph , and a graph is perfect if and only if it does not have an odd one Cycle or its complement graph as the induced subgraph. The bipartite graphs, edge graphs of bipartite graphs, and their complement graphs form four of the five basic classes of perfect graphs that are used to prove the theorem of strong perfect graphs.

For a node , the number of neighboring nodes is called the degree of the node and is referred to as . The sum of degrees for a bipartite graph says that ${\displaystyle \deg(v)}$

${\displaystyle \sum _{v\in V}\deg(v)=\sum _{u\in U}\deg(u)=|E|}$

The degree sequence of a bipartite graph is the pair of lists that contain the nodal degrees of the two partition classes and . For example, the complete bipartite graph has the degree sequence . Isomorphic bipartite graphs have the same degree sequence. However, the degree sequence does not uniquely identify a bipartite graph in general. In some cases, non-isomorphic two-part graphs can have the same degree sequence. ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle K_{3,5}}$ ${\displaystyle (5,5,5),(3,3,3,3,3)}$

Combinatorics

The number of bipartite graphs increases faster than exponentially with the number of nodes . The following table shows the numbers determined with the help of a computer for : ${\displaystyle n}$ ${\displaystyle n\leq 12}$

Number of bipartite graphs
n	all	coherent
1	1	1
2	2	1
3	3	1
4th	7th	3
5	13	5
6th	35	17th
7th	88	44
8th	303	182
9	1119	730
10	5479	4032
11	32303	25598
12	251135	212780

Algorithms

See also : graph partitioning

With the algorithm from Hopcroft and Karp , a maximum matching can be found in the runtime and the stability number can also be determined from it. ${\displaystyle O(m{\sqrt {n}})}$

With a simple algorithm based on depth-first search , it can be determined in linear running time whether a graph is bipartite and a valid partition or 2- coloration can be determined. A color is assigned to any node and the complementary color to its children. If, when coloring, it is found that two neighboring nodes have the same color, the graph is not bipartite.

The main idea is to assign each node the color that is different from the color of the parent node in depth-first search and assign colors in the main order of depth-first search. This inevitably results in a 2- color coloring of the spanning forest, which is made up of the edges connecting the nodes to their parent nodes, but some edges that do not belong to the forest may not be colored properly. One of the two end nodes of each edge that does not belong to the forest is an ancestor of the other end node. If an edge of this type is discovered during depth-first search, it should be checked whether these two nodes are different colors. If this is not the case, the path in the forest from ancestor to descendant, together with the wrongly colored edge, forms an odd cycle , which is returned by the algorithm along with the result that the graph is not bipartite. However, if the algorithm exits without finding an odd cycle of this type, each edge must be properly colored and the algorithm returns the coloring along with the result that the graph is bipartite.

Alternatively, a similar can algorithm with breadth-first search to be used instead of the depth-first search. Again, each node is given the opposite color to its parent node in the search tree in the order of breadth-first search. When coloring a node, if there is an edge that connects it to a previously colored node of the same color, this edge, together with the paths in the search tree of the breadth-first search of its two endpoints with their last common ancestor, forms an odd cycle . If the algorithm exits without finding an odd cycle in this way, it must have found a correct coloring and can conclude that the graph is bipartite.

For the average graph with lines or other simple forms in the Euclidean plane , it is possible, with a running time of test if the graph is bipartite and either a 2- coloring or an odd cycle to find, although the graph itself to edges have can. ${\displaystyle n}$ ${\displaystyle {\mathcal {O}}(n\cdot \log(n))}$ ${\displaystyle {\mathcal {O}}(n^{2})}$

Matchings

→ Main article : Matching (graph theory)

A matching in a graph is a subset of its edges , neither of which have a node in common. Algorithms with polynomial running time are known for many applications with matching, including maximum matching , the Maximum Weight Matching and the Stable Marriage Problem .

In many cases, matching problems are easier to solve for bipartite graphs than for non-bipartite graphs, and many matching algorithms, such as the Hopcroft and Karp algorithm for maximum matchings, only work correctly for bipartite graphs.

As a simple example, let's assume that a group of people is looking for jobs out of a set of jobs, and not all people are suitable for all jobs. This situation can be modeled as a bipartite graph with an edge connecting every job seeker with every suitable job. A perfect match describes a possibility to satisfy all job seekers at the same time and to fill all jobs. The marriage theorem provides a characterization of the bipartite graphs that enable perfect matching. The National Resident Matching Program in the United States uses matching algorithms to solve this problem for medical students and hospital jobs. ${\displaystyle P}$ ${\displaystyle J}$ ${\displaystyle (P,J,E)}$

generalization

A k-partiter graph is a graph whose node set can be divided into partitions, so that there is no edge between two nodes of a partition. ${\displaystyle k}$

See also

• Matching (graph theory)
• Petri net
• Secretary problem

literature

• Frank Gurski, Irene Rothe, Jörg Rothe, Egon Wanke: Exact algorithms for difficult graph problems , Springer-Verlag, Berlin Heidelberg, 2010, ISBN 978-3-642-04499-1 .
• Sven Krumke, Hartmut Noltemeier: Graph Theoretical Concepts and Algorithms, Vieweg + Teubner Verlag, 2012, ISBN 978-3-8348-1849-2 .

Web links

Wikiversity: A lecture on bipartite graphs as part of a discrete mathematics  course - course materials

Commons : Bipartiter Graph  - collection of images, videos and audio files

Individual evidence

1. ^ Béla Bollobás: Modern Graph Theory . In: Springer (Ed.): Graduate Texts in Mathematics . 184, 1998.
2. ^ Maria Chudnovsky, Neil Robertson, Paul Seymour, Robin Thomas: The strong perfect graph theorem . In: Annals of Mathematics . 164, No. 1, 2006, pp. 51-229. arxiv : math / 0212070 . doi : 10.4007 / annals.2006.164.51 .
3. ↑ sequence A033995 in OEIS
4. ↑ Follow A005142 in OEIS
5. ^ Robert Sedgewick: Algorithms in Java, Part 5: Graph Algorithms . In: Addison-Wesley . 2004, pp. 109-111.
6. ^ Jon Kleinberg, Éva Tardos: Algorithm Design . In: Addison-Wesley . 2006, pp. 94-97.
7. ^ David Eppstein: Testing bipartiteness of geometric intersection graphs . In: ACM Transactions on Algorithms . 5, No. 2, 2009, p. Art. 15. arxiv : cs.CG/0307023 . doi : 10.1145 / 1497290.1497291 .
8. ↑ Ravindra K. Ahuja, Thomas L. Magnanti, James B. Orlin: Network Flows: Theory, Algorithms, and Applications . In: Prentice Hall . 1993, pp. 461-509.
9. ↑ John E. Hopcroft, Richard M. Karp: An n ^5/2 algorithm for maximum matchings in bipartite graphs . In: SIAM Journal on Computing . 2, No. 4, 1973, pp. 225-231. doi : 10.1137 / 0202019 .