Subgraph

The term subgraph in describing graph theory a relationship between two graphs . Another word for subgraph is subgraph . A graph is a subgraph of the graph if all nodes and edges of are also included in . In other words: A subgraph is created from a graph by removing some nodes and edges from . When removing a node, all incident edges must also be removed. ${\displaystyle H}$ ${\displaystyle G}$ ${\displaystyle H}$ ${\displaystyle G}$ ${\displaystyle H}$ ${\displaystyle G}$ ${\displaystyle G}$

Definitions

A graph is called a subgraph or subgraph or subgraph of if its node set is a subset of and its edge set is a subset of , i.e. and holds. ${\displaystyle G_{1}=(V_{1},E_{1})}$ ${\displaystyle G_{2}=(V_{2},E_{2})}$ ${\displaystyle V_{1}}$ ${\displaystyle V_{2}}$ ${\displaystyle E_{1}}$ ${\displaystyle E_{2}}$ ${\displaystyle V_{1}\subseteq V_{2}}$ ${\displaystyle E_{1}\subseteq E_{2}}$

The reverse is then called supergraph or upper graph of . ${\displaystyle G_{2}}$ ${\displaystyle G_{1}}$

These terms are not uniform. In the below text book by Klaus Wagner , only the term in this general subgraph used, and a sub-graph defined as a subgraph, which additionally has the property that each edge of the two nodes from connecting also an edge in is. In Claude Berge's textbook , subgraph also means that is, and subgraph means that and every edge out that connects two nodes in is also an edge in , the general case is then called part-subgraph there . It is therefore advisable to check the definition used with each author. ${\displaystyle G_{2}}$ ${\displaystyle G_{1}}$ ${\displaystyle G_{1}}$ ${\displaystyle V_{1}=V_{2}}$ ${\displaystyle V_{1}\subset V_{2}}$ ${\displaystyle G_{2}}$ ${\displaystyle G_{1}}$ ${\displaystyle G_{1}}$

In the case of a node-weighted or edge-weighted graph , it is also required of a subgraph that the weight function of must be compatible with the weight function of , i. H. for each node is valid and for each edge is considered . ${\displaystyle G_{2}}$ ${\displaystyle G_{1}}$ ${\displaystyle g_{1}}$ ${\displaystyle G_{1}}$ ${\displaystyle g_{2}}$ ${\displaystyle G_{2}}$ ${\displaystyle v\in V_{1}}$ ${\displaystyle g_{1}(v)=g_{2}(v)}$ ${\displaystyle e\in E_{1}}$ ${\displaystyle g_{1}(e)=g_{2}(e)}$

If it is also true for a subgraph that all edges between the nodes in contains that are also present in, then one denotes the subgraph of induced by and also notes this down . An induced subgraph is therefore always uniquely determined by the supergraph and the selected node set. For a node-set is denoted by the induced subgraphs consisting by omitting the node is created and their incident node edges, ie . ${\displaystyle G_{1}}$ ${\displaystyle E_{1}}$ ${\displaystyle V_{1}}$ ${\displaystyle E_{2}}$ ${\displaystyle G_{1}}$ ${\displaystyle V_{1}}$ ${\displaystyle G_{2}}$ ${\displaystyle G_{2}[V_{1}]}$ ${\displaystyle W\subseteq V}$ ${\displaystyle G\setminus W}$ ${\displaystyle G=(V,E)}$ ${\displaystyle W}$ ${\displaystyle G\setminus W=G[V\setminus W]}$

A subgraph of that contains all nodes of its supergraph is called a spanning subgraph or factor . ${\displaystyle G_{1}=(V,E_{1})}$ ${\displaystyle G_{2}=(V,E_{2})}$

Examples

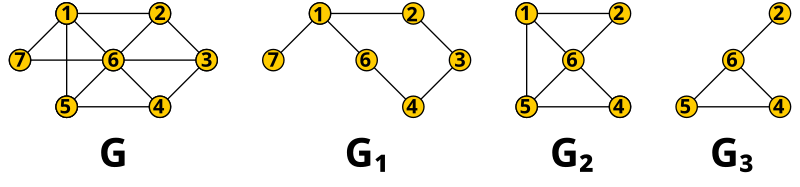
In the following figure, the graphs , and subgraphs of , but only and are induced subgraphs. arises from by omitting the nodes and their incident edges, so is . At the same time there is also an induced subgraph of . ${\displaystyle G_{1}}$ ${\displaystyle G_{2}}$ ${\displaystyle G_{3}}$ ${\displaystyle G}$ ${\displaystyle G_{2}}$ ${\displaystyle G_{3}}$ ${\displaystyle G_{3}}$ ${\displaystyle G}$ ${\displaystyle 1,3,7}$ ${\displaystyle G_{3}=G\setminus \{1,3,7\}}$ ${\displaystyle G_{3}}$ ${\displaystyle G_{2}}$

Examples of subgraph relationships

See also

• Subdivision graph
• Minor (graph theory)
• Kuratowski's theorem
• Krausz partition

literature

• Reinhard Diestel: graph theory. 4th edition. Springer-Verlag, Berlin Heidelberg 2010, ISBN 978-3-642-14911-5 . (354 pages, online )
• Lutz Volkmann: Fundamente der Graphentheorie , Springer (Vienna) 1996, ISBN 3-211-82774-9 ( newer online version "Graphs on all corners and edges" ; PDF; 3.51 MB)

Individual evidence

1. ↑ Klaus Wagner: Theory of Graphs , BI University Pocket Books (1969), Volume 248, Chap. I, §3, definition 4
2. ↑ Claude Berge: Programs, games, transport networks , Teubner-Verlag 1969, part of the time, chap. I, paragraph 1, page 121