Kuratowski's theorem

The Kuratowski's theorem (after Kazimierz Kuratowski ) is a set of the graph theory , the important statements on planar graphs makes and the question of the planarity (planarity) of a graph answered.

Planarity

Animation: the Petersen graph contains as a minor and is therefore not planar.

{\ displaystyle K_ {3,3}}

In general terms, a graph is planar (flattenable) if and only if it is possible to draw the graph in the plane in such a way that the edges of the graph do not intersect. The edges may only touch in the nodes of the graph.

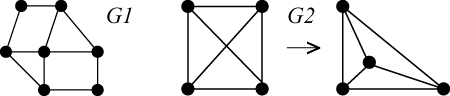
The following two graphs are planar, the planarity of only becoming apparent when you draw differently. ${\ displaystyle G_ {2}}$ ${\ displaystyle G_ {2}}$

Fig. 1: Example graphs G1 and G2

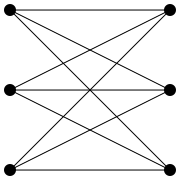
The graphs K ₅ and K _3,3

Fig. 2:

{\ displaystyle K_ {5}}

Fig. 3:

{\ displaystyle K_ {3,3}}

Kuratowski's theorem uses two special graphs: and . When it is the complete graph with 5 nodes (see Fig. 2), in a completely bipartite graph , which is divided into two each three-element subsets (see Fig. 3). Both graphs are not planar. They are actually the smallest non-planar graphs around, which follows directly from Kuratowski's theorem. ${\ displaystyle K_ {5}}$ ${\ displaystyle K_ {3,3}}$ ${\ displaystyle K_ {5}}$ ${\ displaystyle K_ {3,3}}$