König's Theorem (graph theory)

The set of King is a mathematical theorem from graph theory , which for bipartite graphs a relationship between a greatest pairing and a minimum vertex cover shows. It reads:

In a bipartite graph, the size of a largest pairing is equal to the size of a minimum node coverage.

The theorem is named after the Hungarian mathematician Dénes Kőnig , who proved it in 1931. Independently of König, the mathematician Jenő Egerváry , also in 1931, proved a more general formulation of the theorem for weighted graphs . That is why the sentence is sometimes referred to as König and Egerváry's sentence.

example

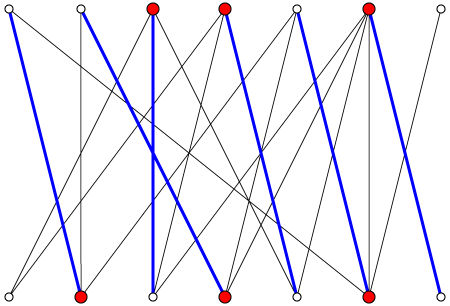
An example of a bipartite graph, with the greatest pairing (blue) and the minimum vertex coverage (red):

algorithm

This algorithm describes how the minimum node coverage is obtained from a largest pairing. A largest pairing can be calculated, for example, using the Hopcroft and Karp algorithm. The two sets of nodes of the bipartite graph are denoted by (above) and (below). ${\displaystyle O}$ ${\displaystyle U}$

1. Calculate a largest match.
2. All nodes from not included in the pairing are inserted into. ${\displaystyle O}$ ${\displaystyle T}$
3. We trace from these nodes to edges that are not included in the pairing . All visited nodes are inserted into. ${\displaystyle U}$ ${\displaystyle T}$
4. From the nodes reached in this way , we go back to the edges contained in the pairing . All visited nodes are inserted into. ${\displaystyle U}$ ${\displaystyle O}$ ${\displaystyle T}$
5. Repeat the previous two steps until no more nodes are added. ${\displaystyle T}$
6. The minimum node overlap results from ${\displaystyle (O\setminus T)\cup (U\cap T)}$

Variant for weighted graphs

Independently of König, the mathematician Jenő Egerváry proved a variant of the theorem for weighted graphs . Here we consider bipartite graphs with a weight function that assigns a nonnegative integer to each edge in the graph. A weighted vertex coverage of is a function that assigns a nonnegative integer to every vertex in the graph, so that applies to all edges . The weight of is given by. The sentence then reads as follows: ${\displaystyle G=(V=A\cup B,E)}$ ${\displaystyle d\colon E\to \mathbb {N} }$ ${\displaystyle d}$ ${\displaystyle \pi \colon V\to \mathbb {N} }$ ${\displaystyle \pi (u)+\pi (v)\geq d(\{u,v\})}$ ${\displaystyle \{u,v\}\in E}$ ${\displaystyle \pi }$ ${\displaystyle \sum _{v\in V}\pi (v)}$

In a complete bipartite graph with and a weight function , the maximum weight of a pairing corresponds to the minimum weight of a weighted node cover of . ${\displaystyle G=(V=A\cup B,E)}$ ${\displaystyle |A|=|B|}$ ${\displaystyle d\colon E\to \mathbb {N} }$ ${\displaystyle d}$

Individual evidence

1. ^ Klaus Wagner: Graph theory. Bibliographisches Institut Hochschultaschenbücher, Mannheim 1970, ISBN 3-411-00248-4 , sentence 9.9
2. ↑ Jenő Egerváry: Matrixok kombinatorius tulajdonságairól . In: Matematikai és Fizikai Lapok . tape 38 , 1931, p. 16-28 . (On combinatorial properties of matrices)
3. ↑ ^{a b} Harold W. Kuhn: On combinatorial properties of matrices . In: George Washington University (Ed.): Logistics Papers . tape 11 , 1955, pp. 1-11 .

Web links

Wikiversity: A Proof of Koenig's Theorem as part of a Discrete Mathematics  course - Course Materials

• Eric W. Weisstein : König-Egeváry Theorem . In: MathWorld (English).
• Proof of König's Theorem (PDF; 286 kB)