Breadth-first search

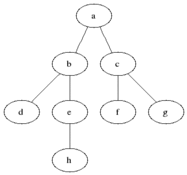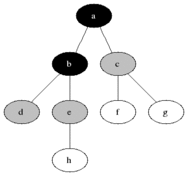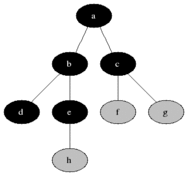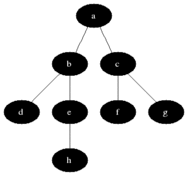
Breadth-first search ( English breadth-first search , BFS ) is a method in computer science for browsing or traversing the nodes of a graph . It is one of the uninformed search algorithms . In contrast to the depth- first search , all nodes that are directly accessible from the starting node are entered first. Only then are the following nodes entered (see illustration).

Working method

The breadth-first search is an uninformed search that searches the graph in breadth for an element by expanding the individual levels of the graph, starting from the start node .

First a starting node is selected. From this node , each edge is now examined and tested whether the opposite node has already been discovered or is the element being sought. If this is not yet the case, the corresponding node is stored in a queue and processed in the next step. It should be noted here that breadth-first search always processes all nodes of the same level first, and not, like depth-first search, follows a path into the depth. After all edges of the exit node have been considered, the first node is removed from the queue and the process is repeated. ${\ displaystyle u}$ ${\ displaystyle (u, v)}$ ${\ displaystyle v}$

A map of Germany with the connections between some cities.

The tree that arises when you apply BFS to the map and start in Frankfurt.

Another example of breadth-first search

algorithm

Determine the node where the search should begin, mark it as visited and save it in a queue .
Pick a node from the top of the queue.
- If the element you are looking for was found, cancel the search and return "found".
- Otherwise, append all previously unmarked successors of this node to the end of the queue and mark them as visited.
If the queue is empty, then every node has already been examined. End the search and return "not found".
Repeat step 2.

The algorithms formulated below are to be understood as pseudocode and, for reasons of readability, only indicate whether the target node has been found. Further information that is important in use cases - such as B. the current path depth or the previous search path - could also be inserted.

To put it recursively :

BFS(start_node, goal_node) {
  return BFS'({start_node}, ∅, goal_node);
}
BFS'(fringe, visited, goal_node) {
  if(fringe == ∅) {
    // Knoten nicht gefunden
    return false;
  }
  if (goal_node ∈ fringe) {
    return true;
  }
  return BFS'({child | x ∈ fringe, child ∈ expand(x)} \ visited, visited ∪ fringe, goal_node);
}

Formulated as a loop :

BFS(start_node, goal_node) {
 for(all nodes i) visited[i] = false; // anfangs sind keine Knoten besucht
 queue.push(start_node);              // mit Start-Knoten beginnen
 visited[start_node] = true;
 while(! queue.empty() ) {            // solange queue nicht leer ist
  node = queue.pop();                 // erstes Element von der queue nehmen
  if(node == goal_node) {
   return true;                       // testen, ob Ziel-Knoten gefunden
  }
  foreach(child in expand(node)) {    // alle Nachfolge-Knoten, …
   if(visited[child] == false) {      // … die noch nicht besucht wurden …
    queue.push(child);                // … zur queue hinzufügen…
    visited[child] = true;            // … und als bereits gesehen markieren
   }
  }
 }
 return false;                        // Knoten kann nicht erreicht werden
}

properties

Denote the number of nodes and the number of edges in the graph. Storage space consumption and running time of the algorithm are given in Landau notation . ${\ displaystyle | V |}$ ${\ displaystyle | E |}$

Storage space consumption

Since all nodes discovered so far are stored, the disk space consumption of breadth-first search is . The breadth-first search is usually unsuitable for methods in which the nodes are only generated during the breadth-first search (e.g. the branch & bound method ) due to the large amount of space required. A method that is similar to breadth-first search , but which usually works with significantly less memory, is iterative depth-first search . ${\ displaystyle {\ mathcal {O}} (| V |)}$

running time

Since in the worst case all possible paths to all possible nodes have to be considered, the duration of the breadth-first search is . Note that between and can vary depending on how thin the graph is. ${\ displaystyle {\ mathcal {O}} (| V | + | E |)}$ ${\ displaystyle {\ mathcal {O}} (| E |)}$ ${\ displaystyle {\ mathcal {O}} (1)}$ ${\ displaystyle {\ mathcal {O}} (| V | ^ {2})}$

If the number of nodes in the graph is known in advance and additional data structures are used to determine which node is already on the queue have been added which can space complexity than be expressed. This is in addition to the memory space required for the graph itself, which can vary depending on the graph representation used by an implementation of the algorithm. ${\ displaystyle {\ mathcal {O}} (| V |)}$

completeness

If there are only a finite number of alternatives in each node , then breadth-first search is complete. This means that if a solution exists, it will be found. This is independent of whether the underlying graph is finite or not. However, if no solution exists, the breadth-first search diverges for an infinite graph.

When analyzing algorithms , it is assumed that the input for breadth-first search is a finite graph that is explicitly represented as an adjacency list or similar. In the application of graph - traversal in artificial intelligence , however, the input may be an implicit representation of an infinite graph. In this context, a search method is described as complete when it is guaranteed that a target state will be found, if one exists. Breadth-first search is complete, but depth-first search is not. When applied to an infinite number of graphs that are implicitly represented, breadth-first search will eventually find the target state, but depth-first search can get lost in parts of the graph that have no target state and never return.

Optimality

Every solution found by breadth-first search has the shortest distance to the root node. If edge weights are introduced, the result that is closest to the starting node does not necessarily have to be the result with the lowest path costs. This problem can be avoided by expanding the breadth-first search to include a uniform cost search. However, if all edge weights are equivalent, then every solution found by breadth-first search is optimal, since in this case the solution that is closest to the starting node is also the solution with the lowest costs. Whether existing solutions can be found at all depends on the finiteness properties of the search tree (see completeness).

The uniform-cost search ( English uniform-cost search ) is an extension of the breadth-first search for graphs having weighted edges. The algorithm visits nodes in the order of ascending path costs from the root node and is therefore usually implemented with a priority queue in which all neighbors not yet visited of already visited nodes are managed with the path length as a key. Optimality is only guaranteed for non-negative edge weights.

application

Breadth-first search can be used for many questions in graph theory . Some are:

Find all nodes within a connected component
Check whether the given graph is a pair and, if necessary, find a feasible 2-coloring of its nodes
Find a shortest path between two nodes u and w (unweighted edges)
Shortest-circle problem

literature

Thomas H. Cormen, Charles Leiserson, Ronald L. Rivest , Clifford Stein: Introduction to Algorithms. MIT Press, 2nd edition 2001, ISBN 0-262-53196-8
Sven Oliver Krumke, Hartmut Noltemeier: Graph theory concepts and algorithms . 3. Edition. Springer Vieweg, 2012, ISBN 978-3-8348-1849-2

Web links

Commons : breadth-first search - collection of images, videos, and audio files

Wikibooks: Breadth First Search - Implementations in the Algorithm Collection

Individual evidence

↑ Winfried Hochstättler: Algorithmic Mathematics . Springer, Heidelberg, a. a. 2010, ISBN 978-3-642-05421-1 , pp. 56-58 .
^ Coppin, B. (2004). Artificial intelligence illuminated. Jones & Bartlett Learning. pp. 79-80.
↑ Dieter Jungnickel: Graphs, Networks and Algorithms. BI Wissenschaftsverlag, 3rd edition 1994, ISBN 3-411-14263-4 , pp. 95-100

[1] Winfried Hochstättler: Algorithmic Mathematics . Springer, Heidelberg, a. a. 2010, ISBN 978-3-642-05421-1 , pp. 56-58 .

[2] Coppin, B. (2004). Artificial intelligence illuminated. Jones & Bartlett Learning. pp. 79-80.

[3] Dieter Jungnickel: Graphs, Networks and Algorithms. BI Wissenschaftsverlag, 3rd edition 1994, ISBN 3-411-14263-4 , pp. 95-100