Coloring (graph theory)
A coloring of an undirected graph assigns to each node or each edge in the graph to a color.
In graph theory , one mostly only deals with so-called “permissible” or “valid” colors (see below), and tries to develop algorithms that find a valid color with as few colors as possible for a given graph. Problems from discrete mathematics , but also non-mathematical questions can sometimes be translated into a coloring problem, so the existence or non-existence of such algorithms is also of interest outside of graph theory.
Knot dyeing
If an undirected graph without multiple edges and a mapping of the set of nodes into the set of natural numbers is called a node coloring of . The elements of are called colors . In some cases, maps are also considered in any countable quantities and not in the natural numbers . But this is not important, it is only necessary that the colors can be distinguished. One calls valid or admissible if any two neighboring nodes are not of the same color:
where denotes the set of neighbors of .
In this case k is called knot-colourable if there is a valid knot coloring of such that only colors are used, that is .
A feasible vertex coloring of a graph is a partition of its vertex set into independent sets. A subset of the node set of a graph is called independent if it does not contain two neighboring nodes.
With a complete node coloring there is an edge for each pair of colors , so that with and is colored with . This means that for each pair of colors there are neighboring nodes that are colored with these colors.
Number of colorations
When a graph is colorable, there is a smallest number such that the graph node is colorable. This number is called the chromatic number or node color number of the graph and is usually referred to as. If there is no coloring for so many colors, one sets symbolically .
The chromatic polynomial of a graph indicates the number of permissible colors for each number .
Bandwidth
Is a simple graph with nodes and one -to-one coloring of the nodes, then called
the bandwidth ( English bandwidth ) of the graph with respect to and
the range of the graph . The determination of the bandwidth is one of the few graph-theoretic problems that is NP-complete for trees .
Properties of the chromatic number
Assigning different colors to different nodes always results in correct coloring, so the following applies
The only graphs that can be 1-colored are edgeless graphs. A complete graph with nodes requires colors. In the case of optimal coloring, at least one of the edges of the graph must exist between each pair of color classes , so the following applies
If a clique contains the size , at least colors are required to color this clique, that is, the chromatic number is at least as large as the clique number :
Every -partite graph can be -node-colored , the partition classes correspond exactly to the colors here. In particular, all bipartite graphs can be 2-colored. However, every 2-colorable graph is also bipartite. Since it is a graph in polynomial time on Bipartitheit can test accordingly also the 2-Färbbarkeitsproblem in polynomial is releasable.
According to the four-color theorem , every planar graph can be 4-colored.
Greedy coloring shows that any graph can be colored with one color more than the maximum node degree :
Complete graphs have and , and odd cycles have and , so this limit is the best possible for these graphs. In all other cases the limit can easily be improved. The set of Brooks shows that these are also the only examples: For each connected graph that is neither complete nor a cycle of odd length, its chromatic number is always less than or equal to the maximum degree of the graph.
Limits for the chromatic number
Hoffman's limit
Let be a real symmetric matrix such that is if there is no edge of . Define where and are the largest and smallest eigenvalues of . If one defines , then the following applies:
Vector chromatic number
Let be a positive semi-definitive matrix such that if there is an edge of . Defined as the smallest for which such a matrix exists. Then:
Lovász number
The Lovász number of a complementary graph is also a lower limit for the chromatic number:
Broken Chromatic Number
The fractional chromatic number of a graph is also a lower bound for the chromatic number:
These limits are ordered as follows:
Limits for the chromatic index
An edge coloring of is a node coloring of its edge graph and vice versa, so:
There is a strong relationship between the edge colorability and the maximum of the graph. Since all edges connected to the same node need their own color, the following applies:
The following sentences also apply:
König theorem :when is bipartite .
Vizing's theorem : A graph with maximum degree has the edge chromatic number or.
Nodal coloring of planar graphs
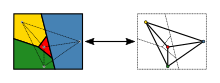
One of the classic problems of graph theory is the question of how many colors are minimally needed to color a map in such a way that two countries that border each other are not the same color. This problem can easily be converted into a knot coloring problem (see figure). The equivalent question in graph theory is: What is the chromatic number of a planar graph ? The four-color theorem states that the chromatic number of a planar graph is at most 4. If the graph does not contain a triangle, it can even be colored with 3 nodes. Nevertheless, the determination of the chromatic number is NP-difficult even for planar graphs.
Algorithms
The determination of the chromatic number of a graph is NP-difficult , which means that - from the point of view of complexity theory - there is probably no algorithm that solves this problem efficiently. The determination of the chromatic number is also one of the problems of Karp's 21 NP-complete problems and thus one of the first problems for which NP-completeness was shown. Exceptions are bipartite graphs and perfect graphs . The decision problem as to whether a given graph is bipartite has linear time complexity and can be solved with depth-first search , for example . In the case of perfect graphs, there are polynomial time algorithms for calculating the chromatic number.
The knot coloring problem is NP-complete .
The currently practically best algorithm for determining a node color is based on a column generation approach (see literature). Furthermore, there are many coloring heuristics that search for good coloring using certain methods and thus, if successful, provide an upper bound for the chromatic number.
Applications
Timetable problems can be formulated as graph coloring problems: The nodes of the graph are the events to be placed, and an edge is inserted between two events that cannot take place at the same time. In school that would be B. Lessons taught by the same teacher and lessons in the same class. The possible colors correspond to the assignable time windows.
The red-black tree is balanced by coloring the knots.
In the same way, for example, register allocation problems in processors , bandwidth allocation problems and also many problems from mathematics can be formulated as graph coloring problems .
Generalizations
A generalization of node coloring is the concept of list coloring . Each node is assigned a “list” of available colors and the graph should now receive a valid color from these lists. There is also total coloring , in which both nodes and edges are to be colored.
literature
- Reinhard Diestel: graph theory . Springer-Verlag, Heidelberg, Germany 2000, ISBN 3-540-67656-2 . http://diestel-graph-theory.com/german/index.html
- Anuj Mehrotra, Michael A. Trick: A column generation approach for graph coloring . In: INFORMS Journal on Computing . 8, No. 4, 1996, pp. 344-354. doi : 10.1287 / ijoc.8.4.344 .
Individual evidence
- ↑ Hopcroft, John E .; Motwani, Rajeev ; Ullman, Jeffrey D. (2006). Introduction to Automata Theory, Languages, and Computation (3rd ed.) . Addison-Wesley. ISBN 8178083477 , page 474.
Web links
- Andy Theiler: PHP implementation of the edge coloring algorithm (generate game plan)