Red-black tree

Red-black tree
	Complexity in elements ${\displaystyle n}$
space	${\displaystyle {\mathcal {O}}(n)}$
surgery	on average, amortized	Worst case
Search	${\displaystyle {\mathcal {O}}(\log n)}$	${\displaystyle {\mathcal {O}}(\log n)}$
Cross step	${\displaystyle {\mathcal {O}}(1)}$	${\displaystyle {\mathcal {O}}(\log n)}$
Min, max	${\displaystyle {\mathcal {O}}(\log n)}$	${\displaystyle {\mathcal {O}}(\log n)}$
Insert	${\displaystyle {\mathcal {O}}(1)}$†	${\displaystyle {\mathcal {O}}(\log n)}$
Clear	${\displaystyle {\mathcal {O}}(1)}$†	${\displaystyle {\mathcal {O}}(\log n)}$
†without navigation (only rebalancing )
Space and time complexities

A red-black tree , also RS-tree or RB-Tree , ( English red-black tree or RB tree ) is a data structure of type binary search tree , the "very fast" access guarantees the data stored in their keys. Red-black trees were first described in 1972 by Rudolf Bayer , who named them symmetric binary B-trees . The current name goes back to Leonidas J. Guibas and Robert Sedgewick , who introduced the red-black color convention in 1978. The fast access times to the individual elements stored in the red-black tree (mostly pairs of the type (key, value)) are achieved through two requirements that determine the balance of the tree in such a way that the height of a tree with elements is never greater than can be. Thus, the most important operations in search trees - search , insert and delete - are guaranteed to be carried out in (see  Landau symbols ). ${\displaystyle n}$ ${\displaystyle 2\log _{2}(n\!+\!2)\!\!-\!\!2}$ ${\displaystyle {\mathcal {O}}(\log n)}$

definition

In addition to the properties of the binary search tree everyone has nodes of the red-black tree another attribute, called color , which can take two values, called " red " (English. RED ) and " black " (English. BLACK ). This coloring has to meet the following two requirements :

Requirement ! RR   ("Not Red Red"):	A child node of a red node is black.
Requirement S # =   ("Black number equal"):	Any path from a given node to one of its descendants with exit degree ≤1, i.e. H. to leaves or half leaves , hereinafter referred to as " path ends " for short , contains the same number of black nodes.

Red-black tree
of tree height 4 and black height 2

Is a direct consequence of the demands that a half sheet (eg. The node in the example tree) black and his (single) child (nodes must be red), because both path ends, and the path to the end of the path _left is to knot exactly the shorter. ${\displaystyle {\mathsf {R}}}$ ${\displaystyle {\mathsf {1}}}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {6}}}$ ${\displaystyle {\mathsf {1}}}$ ${\displaystyle {\mathsf {6}}}$

From both requirements together it follows immediately that a black knot that is not the root has a sibling.

Black height, tree height

To all paths of path end root same number of black nodes is the black level ( English black height called): the tree , but also its root . According to this definition, a (real) node with black level 0 is a red leaf (its tree height is 1), such as the nodes in the example tree . A (real) black node has a black level ≥ 1. The red nodes but also the black nodes have black level 1. The black nodes have tree height 2, the nodes tree height 1, and is the only node with degree 1, the only half-leaf. ${\displaystyle s}$ ${\displaystyle {\mathsf {6,22,27}}}$ ${\displaystyle {\mathsf {8,17}},}$ ${\displaystyle {\mathsf {1,11,15,25}},}$ ${\displaystyle {\mathsf {1,25}}}$ ${\displaystyle {\mathsf {11,15}}}$ ${\displaystyle {\mathsf {1}}}$

The most important property of red-black trees is ensured by the two requirements:

If the height of the tree is black, then because of the requirement S # = there are exactly black nodes on a path from the root to the end of the path , but because of the requirement ! RR at most one red node more than black, i.e. a maximum of nodes. Thus applies to the number of all nodes in the tree , so that the red-black tree is always good enough balance is - definitely so well that the relationship between the tree height for the true, and the logarithm of the number of nodes is limited. This logarithmic restriction, which is formally proven in §  Height proof, is at the same time the information-theoretical optimum, i.e. H. there is no binary tree with a smaller maximum path length ${\displaystyle s}$ ${\displaystyle s}$ ${\displaystyle 2s\!+\!1}$ ${\displaystyle n}$ ${\displaystyle 2^{s}\!\!-\!\!1\leq n\leq 2^{2s+1}\!\!-\!\!1}$ ${\displaystyle h,}$ ${\displaystyle s\leq h\leq 2s\!+\!1}$ ${\displaystyle n}$ ${\displaystyle h\!\!-\!\!1\in {\mathcal {O}}(\log n).}$

In the case of the highlighted search , insert and delete operations , the effort required at one level of the tree is constant. So the running time is at most proportional to the number of nodes in a path, which is again limited by the height, which in turn is limited by the logarithm of the number of nodes.

NIL node

This article adopts the view shown in the article Binary Search Tree in Fig. 1A and common in many tree structures, in which the nodes carry the keys ( "node-oriented storage" ), regardless of whether they are internal nodes or (internal) leaves.

The same red-black tree with NIL nodes
(tree and black heights are 4 and 2 - as above)

Very common in the literature on red-black trees is the view shown opposite and in the article Binary Search Tree in Fig. 1B, in which - likewise node-oriented - the nodes carrying the keys are viewed as internal , but the tree is additional nodes, see above so-called " NIL nodes " are attached as external sheets, which are at the ends of the path for the (borderless) intervals ( English also " missing nodes ") between the keys. The representation with NIL nodes brings out one path end at the node as clearly as the paired path ends at the nodes. Nonetheless, the NIL nodes can be implemented both as indistinguishable null pointers (as in the text) and as indiscriminate guard nodes . ${\displaystyle {\mathsf {1}}}$ ${\displaystyle {\mathsf {6,11,15,22,27}}.}$

However, if the NIL nodes are viewed as individual nodes, there is an additional requirement for them, so that the following three requirements arise :

• NIL nodes are black.
• Children of a red knot are black.
• The numbers of black nodes in a path from a given node to each of its NIL nodes are equal.

This second point of view has a negligible benefit for understanding the facts, but in the case of “naive” implementation its influence is rather unfavorable.

Data structure

The following example code , which is formulated in the C programming language , refers to a declaration of the tree node of the following type:

 struct node              // Knotenfeld
  {
   struct node* child[2]; // zwei Zeiger zu Kindknoten,
                          // == NULL bedeutet:
                          //   kein Knoten an dieser Stelle
   byte color;            // RED oder BLACK
   ...                    // Benutzer-Daten (z.B. Schlüssel, Wert)
  } ;

 #define LEFT  0
 #define RIGHT 1
 #define left  child[LEFT]  // -> linker  Kindknoten
 #define right child[RIGHT] // -> rechter Kindknoten
 #define RED   0
 #define BLACK 1

If there is a null pointer at a point in the tree where a pointer to a node is expected syntactically , this should mean, according to the agreement, the absence of a node (a so-called " null node") at this point in the tree (the node is considered spurious ). M. a. W .: the subtree rooted by a NULLnode is empty . His pointer value X == NULL, is less important than the place where this value in the data structure is. This location indicates the graph-theoretical relationships to the other elements of the tree: Without representing a node itself, it can be in a child relationship, and thus also in a sibling and uncle relationship with other nodes - but never be a parent.
Its tree height and black height are both considered 0, and color is not assigned to it either. It has a parent (if it is the root, the tree as the logical parent), but never a pointer to the parent.
Functionally, it corresponds exactly to the NIL node , but without it being given any individuality.

Because of the 1: 1 relationship between a node and the subtree it has rooted, a variable is used indiscriminately in the sample code as a pointer to both the node and the subtree.

If operations for access and administration are added to the data structure red-black tree, then these are only regarded as belonging if they maintain the red-black requirements, in particular by checking the tree after a modifying operation and repairing it if necessary. In this way, the data structure is expanded into an abstract data type (ADT) . In the case of search trees, there is also characterization as a self-balancing tree in English .

Explanation of symbols for the diagrams

The more complex cases of insert and delete operations are outlined in diagrams below. These diagrams highlight the relationships and colors of nodes that are relevant for rebalancing.

A diagram in a left column relates to a first iteration level of a case, while a diagram in the right column describes higher iterations of the same case. Each diagram has at least two sections:

1. In the first section (labeled “before”) the initial constellation.
2. In the second section (labeled “transformed”) the constellation transformed by color change and / or rotation.
3. If the tree is not yet rebalanced, in the third section (labeled "after") the constellation after reassigning the problem node and the other nodes attached to it. ${\displaystyle {\mathsf {N}}}$

Although a first iteration level is in principle included in the higher, it is brought for the sake of greater clarity, without the subtrees of non-positive height.
When deleting, in the first iteration stage the end of the path that has lost a black node (and which corresponds to the problem node, which is a zero node here) is marked by a blue arrow pointing to the left . ${\displaystyle {\mathsf {N}}}$

1. The old problem node ( in the “before” section of a diagram) has a blue outline; and if the operation is not finished, then also the new one (in the “after” section). ${\displaystyle {\mathsf {N}}}$
2. The symbol represents a (real) black and a (real) red knot.
3. The symbol represents a ! RR -compliant at his parent attached sub-tree. It has the black level with than the iteration. ${\displaystyle n\!\!-\!\!1}$ ${\displaystyle n}$
   In the first iteration level the black level is 0. Then the subtree either exists
   • from a red leaf or
   • it is empty when the "knot" is also considered to be a false and zero knot .
4. The triangle (without the small black circular area at the top) symbolizes a ! RR -compliant sub-tree connected to its parent, whose black level is with as the iteration level. Its black height is therefore 1 lower than that of the sub-trees. In the first iteration level, the black level would be negative, which is to be interpreted in such a way that its parent is already a zero node. ${\displaystyle n\!\!-\!\!2}$ ${\displaystyle n}$
5. Twice in a diagram or on a line of synopsis means twice the same node color, black or red.

Navigation operations

The navigation operations , i.e. the various search operations , traversing , searching for the first or last element and the like, leave the tree unchanged (read-only access) and in principle work on any binary search tree . The algorithms and information on complexity there apply to red-black trees as well - with the specification that the height of the red-black tree is always logarithmic to the number of nodes.

The Search of an element (or space) by its key is the most important of the navigation operations. (The (height) balancing of the red-black tree tries to optimize for this operation.) It supports a kind of "direct access" (as opposed to the sequential access of the traversal ) and is usually used as a preceding operation in the Modification operations (insert or delete) are used to find the affected node.

Searching requires a total quasi-order on the set of keys, which is most flexibly implemented by a comparison function . If you want duplicates in the tree, a slightly modified search function is recommended .

Insert operation

The first actions when inserting a new element into the red-black tree are the same as with a binary search tree : The pointer to the new node replaces a null pointer which is at the end of the path and as an indicator for the lack of either the root, if the tree is empty, or - in the case of a key-carrying knot - stands for the absence of the left or right child. ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {P}}}$

In the example code below it is assumed that this direction, which reflects the last not equal result of a search for the key of , is passed in the function parameter ∈ { } . Furthermore, that this search function to is assumed stack of the ancestors of formed has. The pointer that is also transferred points in this stack to the pointer of the direct parent of the node to be inserted. If the tree is empty, <is (and irrelevant). Otherwise is equal to the pointer to the root node, ≥ , and the child direction of the new node. ${\displaystyle {\mathsf {N}}}$ dLEFT,RIGHT struct node* Parents[] ${\displaystyle {\mathsf {P}}}$struct node** pParentpParent&Parents[0]dParents[0]pParent&Parents[0]d

The node is first colored red so that the black height of the tree is retained. ${\displaystyle {\mathsf {N}}}$

The following actions check whether the red-black balance in the tree is maintained and restore it if necessary. This repair is called "rebalancing" ( English rebalancing ), respectively.

The new node (like English node ) is the "problem node " just considered. His parent is (like English parent ). The grandparent is called (like English grandparent ) and the uncle (the sibling of the parent) (like English uncle ). ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {G}}}$ ${\displaystyle {\mathsf {U}}}$

The head of the function RBinsert1for inserting a node after a previously performed and unsuccessful search operation could look like this:

 void RBinsert1(
   RBtree* T,                // -> Rot-Schwarz-Baum
   struct node*   Parents[], // Liste der -> Vorfahren
   struct node** pParent,    // ->-> Nachbarknoten (wird zum Elterknoten von N)
   struct node* N,           // -> einzufügender Knoten
   byte d)                   // (Kindes-)Richtung der Einfügung ∈ {LEFT, RIGHT}
  {
   struct node* P;           // -> Elterknoten von N
   struct node* G;           // -> Elterknoten von P
   struct node* U;           // -> Onkel von N

   N->color = RED;
   if (pParent >= &Parents[0]) // N ist nicht die neue Wurzel
    {
     P = *pParent;    // -> Nachbarknoten (wird zum Elterknoten von N)
     P->child[d] = N; // neuer Knoten als d-Kind von P
     goto Start_E;    // Sprung in die Schleife
    } // end_if
   // pParent < &Parents[0]
   T->root = N; // N ist die neue Wurzel des Baums T.
   return; // Einfügung fertiggestellt

   // Beginn der (do while)-Schleife:
   // Bedingung_E0 trifft NICHT zu: pParent >= &Parents[0]:
   do
    {
     // ===> Es gibt den Elter P von N.
     N = G; // neuer Problemknoten (kann die Wurzel sein)
     P = *pParent; // -> Elterknoten von N
 Start_E:

Insert: the loop for checking and repairing the tree rises from the red leaf to the root. Its invariant is: ${\displaystyle {\mathsf {N}}}$

• The requirement ! RR (“Not Red Red”) applies to all pairs (node ​​← parent) in the tree with at most one exception - the pair ( ← ). ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {P}}}$This is called "Red-injury" ( english red violation viewed), which is defined as "problem nodes." If ! RR also applies there, either because the parent does not exist (case E0) or is black (case E1), then the tree is in red-black form. ${\displaystyle {\mathsf {N}}}$
  ${\displaystyle {\mathsf {P}}}$
• At the beginning of each iteration step, the problem node is red.
• The requirement S # = (“Black number equal”) applies to the whole tree.

The synopsis brings the diagrams in a form that is pointed towards the color constellation.

condition

Case →

rota tion

Zuwei- solution

Result

→ test

${\displaystyle \Delta s}$

${\displaystyle {\mathsf {P}}}$

${\displaystyle {\mathsf {G}}}$

${\displaystyle {\mathsf {U}}}$

x

${\displaystyle {\mathsf {P}}}$

${\displaystyle {\mathsf {G}}}$

${\displaystyle {\mathsf {U}}}$

x

-

E0

-

✓

E1

✓

E2

${\displaystyle {\mathsf {N}}}$: = ${\displaystyle {\mathsf {G}}}$

?

?

?

?

E0

1

i

E3

${\displaystyle {\mathsf {P}}}$↶ ${\displaystyle {\mathsf {N}}}$

${\displaystyle {\mathsf {N}}}$: = ${\displaystyle {\mathsf {P}}}$

O

E4

0

O

E4

${\displaystyle {\mathsf {P}}}$↷ ${\displaystyle {\mathsf {G}}}$

✓

-

E5

✓

Insert: synopsis of the cases

Insert: synopsis of the cases

The possible constellations can be divided into six cases, to which there are transformations (containing rotation and / or recoloring) that lead to the rebalancing of the tree either on the level under consideration or via further iteration steps on higher levels.

In the adjacent table, a case is represented by a line that contains

• the condition , that is the constellation that defines the case and that corresponds to the "before" section of the diagram belonging to the case - if it exists,
• the case number,
• the constellation after transformation and, if applicable, assignment in the Result column group

contains. A constellation consists of a maximum of 4 conditions, namely the colors of the 3 nodes and some cases also require a fourth specification x for the child direction of , namely "o" (like English outer ) stands for a right-right or left-left -Child direction from zu zu and "i" (like English inner ) for right-left or left-right. A cell is left blank if the specification is not important. ${\displaystyle {\mathsf {P}},{\mathsf {G}}}$ ${\displaystyle {\mathsf {U}}.}$ ${\displaystyle {\mathsf {N}},}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {G}}}$

The constellations in the Condition group satisfy the loop invariant, and their logical sum uses them 100%.

The transformation, the case number of which is linked in the Case → column , transforms the input constellation (shown as a subtree in the section of the diagram belonging to the case labeled “before”) into the constellation labeled “transformed”. If there is a checkmark "✓" in the → Test column , the result group reflects this status, with which all red-black requirements are met and with which the insert operation is completed. Otherwise there is the case number of the condition for which the transformed and newly assigned constellation is to be tested, whereby the corresponding assignment, specified in the Assignment column for the problem node, also assigns the nodes and the specification x to the child direction of . The column group Result and the section of the diagram labeled “after” shows the constellation after the assignment; Question marks are in the cells that are important for the following tests. ${\displaystyle {\mathsf {N}},}$ ${\displaystyle {\mathsf {P}},{\mathsf {G}},{\mathsf {U}}}$ ${\displaystyle {\mathsf {N}}}$

In the → Test column , the entry "E0" only occurs with Transformation_E2. It means a new iteration step that begins with the test for the while-Condition_E0 in the do whileloop , two tree levels (one black level ) closer to the root. According to this, the black heights of all subtrees are ≥ 1. Since the number of tree levels corresponds to the height , a maximum of iterations can occur. Now the effort for an iteration is limited (i.e. in ) and thus for the entire insert operation in (with or without searching). The pure rebalancing is in accordance with §  Average and amortized term on average and amortized in ${\displaystyle \Delta s}$ ${\displaystyle h}$ ${\displaystyle {\tfrac {h}{2}}}$ ${\displaystyle {\mathcal {O}}(1)}$ ${\displaystyle {\mathcal {O}}(h)={\mathcal {O}}(\log n)}$ ${\displaystyle {\mathcal {O}}(1).}$

If there is an entry in the Rotation column , a rotation is involved in the transformation. The table shows immediately that an insert operation results in a maximum of two rotations, namely from case E4 to case E3. Because after a rotation there is no new iteration step - the rotations are finally recursive at the end of the last executed iteration.

The direction of the child decides in particular on the following directions of rotation. In case E3, however, it also determines the selection of the case: Has the same child direction as then, the indication x (see synopsis ) must be set to “o” for “outside”, otherwise to “i” for “inside”. ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {N}},}$

In the following example dcode for the Insert operation, the variable holds the child direction of the node. The diagrams always show as the left child. ${\displaystyle {\mathsf {P}}.}$ ${\displaystyle {\mathsf {P}}}$

Each case is explained under its case number and described in detail, including the test (for the condition that characterizes it ) and transformation using a piece of C code .

Insert case E1: The parent of the (red) problem node is black. ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {N}}}$

After this condition is met, there is no pair (node ​​← parent) (anymore) that violates the requirement ! RR . Furthermore, according to the assumption (loop invariant), the number of black nodes is the same on all paths. The tree is then red and black without any further action.

     if (P->color == BLACK) // Bedingung_E1
       // Transformation_E1:
       return; // Einfügung fertiggestellt

     // In den verbleibenden Fällen ist der Elter P rot.
     if (pParent <= &Parents[0]) // Bedingung_E5
       goto Fall_E5; // Der Elter P ist die Wurzel.

In the following, the parent is not the root, so the grandparent exists. Since it is red, it must be black (as in the following cases E2, E3 and E4). ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {G}}}$ ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {G}}}$

${\displaystyle \scriptstyle n=1,}$

Iteration level ${\displaystyle \scriptstyle n\geqslant 2}$

(→ Explanation of symbols)

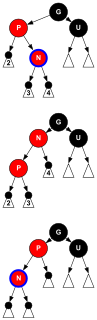
Insert case E2: Both the uncle and the parent of the problem node are red. ${\displaystyle {\mathsf {U}}}$ ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {N}}}$

The color change from and to black and from to red restores the requirement ! RR in the subtree with roots (in both child directions of ). The number of black nodes does not change on any path. Through this Transformation_E2 the “red violation” is shifted up two tree levels (one black level) with a new problem node. ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {U}}}$ ${\displaystyle {\mathsf {G}}}$ ${\displaystyle {\mathsf {G}}}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {G}}}$

     G = *(--pParent);    // Der Großelter G von N existiert.
     d = (P == G->right); // Kindesrichtung von P
     if ((U = G->child[!d]) == NULL || U->color == BLACK)
       goto Test_E3;      // Der Onkel U ist schwarz.
     // Bedingung_E2: N+P+U rot
     // Transformation_E2:
     P->color = BLACK;
     U->color = BLACK;
     G->color = RED;

     // Iteration zwei Ebenen (1 Schwarzebene) höher
    }
   while (--pParent >= &Parents[0])
   // Ende der (do while)-Schleife

Insert case E0: The problem node (here:) is the root. (As noted above, a red root could be colored to black without violating the red-black requirements - which would make the test for Condition_E5 and case E5 superfluous.) ${\displaystyle {\mathsf {G}}}$

After the above Transformation_E2 ! RR (“Not Red Red”) is fulfilled everywhere, and the tree in red-black form.

   // Bedingung_E0: pParent < &Parents[0]
   //               ===> G ist die alte und neue Wurzel des Baums T.
   return; // Einfügung fertiggestellt

${\displaystyle \scriptstyle n=1,}$

Iteration level ${\displaystyle \scriptstyle n\geqslant 2}$

Insert case E3: The problem node has no or one black uncle and has a child direction opposite to that of its red parent d. i.e., is inner grandson. ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {P}},}$ ${\displaystyle {\mathsf {N}}}$

Rotation about interchanges the roles of and namely a left rotate, if left child (d. E. ) , Otherwise a right rotation. (Hereinafter, such a rotation is as -Rotation referred to.) As a result, the paths of the sub-tree are changed so that they by a node of the subtree and the more perform a less. However, since red nodes make the difference in both cases, nothing changes in the number of black nodes, which means that the requirement S # = and the loop invariant remain fulfilled. ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {P}},}$ ${\displaystyle {\mathsf {P}}}$d == LEFTd ${\displaystyle {\mathsf {2}}}$ ${\displaystyle {\mathsf {4}}}$

The result constellation corresponds to the input constellation of case E4 with as the new problem node. ${\displaystyle {\mathsf {P}}}$

 Test_E3:
   if (N != P->child[d]) // Bedingung_E3: N ist innerer Enkel
                         //               && N+P rot && U schwarz
    {
     // Transformation_E3:
     // rotate(P,d); // d-Rotation um P:
     P->child[!d] = N->child[d]; // neuer Elter für Teilbaum 3
     N->child[d] = P;
     G->child[d] = N;
 
     // Neuzuweisung nach der Transformation:
     N = P; // neuer Problemknoten (rot) und äußerer Enkel
     P = G->child[d]; // neuer Elter von N (rot)
    }

${\displaystyle \scriptstyle n=1,}$

Iteration level ${\displaystyle \scriptstyle n\geqslant 2}$

Insert case E4: The problem node has no or one black uncle. His childhood direction is the same as that of d. i.e., is outside grandson. ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {P}},}$ ${\displaystyle {\mathsf {N}}}$

A (non- d) rotation around makes the parent both from and from Because red was, because of the requirement ! RR must be black. If one reverses the colors of and so in the resulting tree is the demand ! RR met again. The requirement S # = is also fulfilled, since all paths that run through one of these three nodes previously ran through and now all run through which - as before the transformation - is now the only black of the three nodes. ${\displaystyle {\mathsf {G}}}$ ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {G}}.}$ ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {G}}}$ ${\displaystyle {\mathsf {G}}}$ ${\displaystyle {\mathsf {P}},}$ ${\displaystyle {\mathsf {G}}}$ ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {G}}}$

   // Bedingung_E4: N ist äußerer Enkel && N+P rot && U schwarz
   // Transformation_E4:
   // rotate(G,!d); // (nicht-d)-Rotation um G:
   G->child[d] = P->child[!d]; // neuer Elter für Teilbaum 3
   P->child[!d] = G;
   if (--pParent >= &Parents[0])
    {
     // Ersetze G bei seinem Elter durch P:
     U = *pParent;
     U->child[G == U->right] = P;
    }
   else // G war die Wurzel
     T->root = P; // P ist die neue Wurzel
 
   P->color = BLACK;
   G->color = RED;
   return; // Einfügung fertiggestellt

Insert case E5: The red parent of the problem node is also the root of the tree. ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {N}}}$

A color change from to black restores the requirement ! RR in the whole tree. On each path, the number of black nodes increases by 1. ${\displaystyle {\mathsf {P}}}$

 Fall_E5:
   // Der Elter P von N ist die Wurzel des Baums.
   // Transformation_E5:
   P->color = BLACK;
   // Da P rot war,
   // erhöht sich die Schwarzhöhe des Baumes um 1.
   return; // Einfügung fertiggestellt
  } // Ende RBinsert1

Delete operation

The deletion of a node, its name is (like English remove ), from a red-black tree is done like a binary search tree . ${\displaystyle {\mathsf {R}}}$

In the event that the root is childless, one takes care of it immediately by replacing it with a null node . If the node has a child or no child at all, it remains the delete node. ${\displaystyle {\mathsf {R}}}$ ${\displaystyle {\mathsf {R}}}$

However, if you have two children, then without ultimately disturbing the sorting order, you take your left or right neighbors in terms of order as the effective delete node (this cannot have a right or a left child!) - of course, after you have previously exchanged the user data. The deletion can therefore be carried out by removing a node with a maximum of one child, a node that is still named. ${\displaystyle {\mathsf {R}}}$ ${\displaystyle {\mathsf {R}}}$

If there is exactly one child, this is denoted by (as in English node ); it must be a red knot. If there is no child, then stand for a zero knot. In both cases, let (like English parent ) be the parent of and (like English direction ) the child direction of (right or left child of ). And in both cases is replaced by as -child of . ${\displaystyle {\mathsf {R}}}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {R}}}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {R}}}$d ${\displaystyle {\mathsf {R}}}$ ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {R}}}$ ${\displaystyle {\mathsf {N}}}$d ${\displaystyle {\mathsf {P}}}$

The following actions check whether the red-black properties in the tree are maintained and restore them if necessary.

Simple cases

If it is red, it has no child. And since all the paths that ran through the red node run less after it has been removed from the tree through a red node, nothing changes in the number of black nodes, which means that the requirement S # = (“black number equals”) remains fulfilled . ${\displaystyle {\mathsf {R}}}$

The case is also easy to solve when is black and has a child. This is then inevitably red. You color it black and turn it into the child's direction in the direction of the child. This removes it from the tree, and the requirement ! RR (“Not Red Red”) remains fulfilled. Furthermore, all paths that ran through the deleted black node now run through its now black child, so that the requirement S # = also remains fulfilled. ${\displaystyle {\mathsf {R}}}$d ${\displaystyle {\mathsf {P}}.}$ ${\displaystyle {\mathsf {R}}}$

Erasing a black sheet

What remains is the case that the knot is black and has no child, i.e. it is a black leaf. After the deletion of the childless root is done above, the root is not. ${\displaystyle {\mathsf {R}}}$ ${\displaystyle {\mathsf {R}}}$

After replacing at by an empty tree, referred to as , the paths leading through the end of the path contain one black node less than before, thus one less than the paths not leading through (if they exist) - in violation of the requirement S # = . ${\displaystyle {\mathsf {R}}}$ ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {N}},}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {N}}}$

The knot was not the root and, since it was black, it had a sibling, the (non- ) child of It is now the sibling of and is called (as in English sibling ). The -child (like English close ) of is the "close" nephew of with the same child direction; the other child (like English distant ) the "distant" nephew. ${\displaystyle {\mathsf {R}}}$d ${\displaystyle {\mathsf {P}}.}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {S}}}$ d ${\displaystyle {\mathsf {C}}}$ ${\displaystyle {\mathsf {S}}}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {D}}}$

The example code below assumes that a previous search function that located the node to be deleted formed the stack from its ancestor and passed its pointer to the delete function. If the root is, then the also passed pointer points in front of this stack ( < ). Otherwise it points in this stack to the pointer to the direct parent of the node to be deleted, and it is ≥ as well as equal to the pointer to the root node. ${\displaystyle {\mathsf {R}}}$ struct node* Parents[] ${\displaystyle {\mathsf {R}}}$struct node** pParentpParent&Parents[0]pParent&Parents[0]Parents[0]

The head of a function RBdelete2for deleting a black node without a child could then look like this: ${\displaystyle {\mathsf {R}}}$

 void RBdelete2(
   RBtree* T,                // -> Rot-Schwarz-Baum
   struct node*   Parents[], // Liste der -> Vorfahren
   struct node** pParent,    // ->-> Elterknoten von R
   struct node* R)           // -> zu löschender Knoten, hier: schwarz
  {
   byte d;                   // Richtung ∈ {LEFT, RIGHT}
   struct node* N = NULL;    // -> Problemknoten (zunächst NULL)
   struct node* P;           // -> Elterknoten von R
   struct node* S;           // -> Geschwisterknoten von N
   struct node* C;           // -> naher  Neffe
   struct node* D;           // -> ferner Neffe

   // R ist nicht die Wurzel, also ist
   //   pParent >= &Parents[0]).
   P = *pParent; // Elter von R
   d = (R == P->right); // Kindesrichtung von R
   // Ersetze R bei seinem Elter P durch NULL:
   P->child[d] = N;
   goto Start_L;        // Sprung in die Schleife

Delete: The loop to check and repair the tree descends from the problem node, i.e. i. first the end of the path , to the root. Its invariant is: ${\displaystyle {\mathsf {N}}}$

• The number of black nodes on paths that do not lead by the offending node is unchanged, and the paths through the problem nodes contain a black node less (so-called "black-injury". English black violation ) - hence the name "problem node" .
• In the first iteration level, the problem node is empty (its pointer value N == NULL). This end of the path with the black violation is symbolized in the representations of the first iteration level by a blue arrow pointing to the left .
  In the higher iteration levels there is a real black node (shown as a problem node with a blue contour). ${\displaystyle {\mathsf {N}}}$
• The requirement ! RR (“Not Red Red”) is met everywhere.

The synopsis brings the diagrams in a form that is pointed towards the color constellation.

condition

Case →

rota tion

Zuwei- solution

Result

→ test

${\displaystyle \Delta s}$

${\displaystyle {\mathsf {P}}}$

${\displaystyle {\mathsf {C}}}$

${\displaystyle {\mathsf {S}}}$

${\displaystyle {\mathsf {D}}}$

${\displaystyle {\mathsf {P}}}$

${\displaystyle {\mathsf {C}}}$

${\displaystyle {\mathsf {S}}}$

${\displaystyle {\mathsf {D}}}$

-

L0

-

✓

L1

${\displaystyle {\mathsf {N}}}$: = ${\displaystyle {\mathsf {P}}}$

?

?

?

?

L0

1

L2

${\displaystyle {\mathsf {P}}}$↶ ${\displaystyle {\mathsf {S}}}$

${\displaystyle {\mathsf {N}}}$: = ${\displaystyle {\mathsf {N}}}$

?

?

L3

0

L3

✓

L4

${\displaystyle {\mathsf {C}}}$↷ ${\displaystyle {\mathsf {S}}}$

${\displaystyle {\mathsf {N}}}$: = ${\displaystyle {\mathsf {N}}}$

L5

0

L5

${\displaystyle {\mathsf {P}}}$↶ ${\displaystyle {\mathsf {S}}}$

✓

Delete: synopsis of the cases

Delete: synopsis of the cases

The possible color constellations can be grouped into six cases, for which there are transformations (including rotation and / or recoloring) that lead to a rebalancing of the tree either on the level under consideration or via further iteration steps on higher levels.

In the adjacent table, a case is represented by a line that contains

• the condition , that is the constellation that defines the case,
• the case number,
• the constellation after transformation and, if applicable, assignment in the Result column group

contains. A constellation (4 columns) consists of the colors of the 4 nodes. A cell is left blank if the information is irrelevant. ${\displaystyle {\mathsf {P}},{\mathsf {C}},{\mathsf {S}},{\mathsf {D}}.}$

The constellations in the Condition group satisfy the loop invariant, and their logical sum uses them 100%. They are sketched again as a subtree in the section labeled “before” in the diagram belonging to the case.

The transformation, the case number of which is linked in the Case → column , transforms the input into a constellation that is shown in the section of the diagram of the case labeled "transformed". If there is a checkmark "✓" in the → Test column , the Result group reflects the final result and the delete operation is completed by the transformation. Otherwise, there is the case number of the condition for which the transformed and newly assigned constellation is to be tested, with the corresponding assignment, given in the Assignment column for the problem node, also clearly defining the nodes . The column group Result and the section of the diagram labeled “after” shows the constellation after the assignment; Question marks are placed next to the nodes whose color is important in the following tests. ${\displaystyle {\mathsf {N}},}$ ${\displaystyle {\mathsf {P}},{\mathsf {C}},{\mathsf {S}},{\mathsf {D}}}$

The entry "L0" only occurs in Transformation_L1 and means a new iteration step on the level 1 higher in the tree (also a black level ), starting with the test for Condition_L0. According to this, the black heights of all subtrees are ≥ 1. The number of levels corresponds to the height , so that at most iterations can occur. Now the effort for an iteration is limited (i.e. in ) and thus the rebalancing effort is even constant on average for the entire delete operation in accordance with §  Average and amortized runtime . ${\displaystyle \Delta s}$ ${\displaystyle h}$ ${\displaystyle h}$ ${\displaystyle {\mathcal {O}}(1)}$ ${\displaystyle {\mathcal {O}}(h)={\mathcal {O}}(\log n).}$

If there is an entry in the Rotation column , a rotation is involved in the transformation. And the table shows that a deletion requires a maximum of three rotations (from case L2 to L4 to L5). Because after a rotation there is no new iteration step - the rotations are finally recursive at the end of the last iteration.

In the following example code, the child direction (variable d) determines both the following rotational directions and the child direction of the nephews and of . ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {C}}}$ ${\displaystyle {\mathsf {D}}}$ ${\displaystyle {\mathsf {N}}}$

   do // Beginn der (do while)-Schleife
    { // Bedingung_L0 trifft NICHT zu: pParent >= &Parents[0]:
     N = P; // neuer Problemknoten (kann die Wurzel sein)
     P = *pParent;
     d = (N == P->right); // Kindesrichtung von N
 Start_L:
     S = P->child[!d]; // Geschwister von N
     if (S->color == RED)
       goto Fall_L2; // Bedingung_L2: S rot ===> P+C+D schwarz
     // S ist schwarz:
     if (((D = S->child[!d]) != NULL) && (D->color == RED))
       goto Fall_L5; // der ferne Neffe D ist rot
     if (((C = S->child[ d]) != NULL) && (C->color == RED))
       goto Fall_L4; // der nahe  Neffe C ist rot
     // Beide Neffen sind == NULL (erste Iteration) oder schwarz (später).
     if (P->color == RED)
       goto Fall_L3; // P rot && C+S+D schwarz <==> Bedingung_L3

The diagrams for the cases only show one child direction, and that is when the problem node is always drawn to the left of during the delete operation . ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {P}}}$

Each case is explained under its case number and described in detail, including the test (for the condition that characterizes it) and transformation using a piece of C code.

${\displaystyle \scriptstyle n=1,}$

Iteration level ${\displaystyle \scriptstyle n\geqslant 2}$

(→ Explanation of symbols)

Clear case L1: The parent of the problem node and the siblings are black, as are the children and from where they exist. ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {S}}}$ ${\displaystyle {\mathsf {C}}}$ ${\displaystyle {\mathsf {D}}}$ ${\displaystyle {\mathsf {S}},}$

The color change of the node from black to red decreases the number of black nodes by 1 in all paths that lead through . This applies to exactly those paths that lead through but not through , which latter paths previously contained exactly black nodes. So there are black nodes in the paths that lead through and in those that do not lead through - if there are still some. Thus, the first condition of the loop invariant is now fulfilled as a problem node. ${\displaystyle {\mathsf {S}}}$ ${\displaystyle {\mathsf {S}}}$ ${\displaystyle s}$ ${\displaystyle s\!\!-\!\!1}$ ${\displaystyle {\mathsf {P}},}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle s\!\!-\!\!1}$ ${\displaystyle s\!\!-\!\!1}$ ${\displaystyle {\mathsf {P}}}$ ${\displaystyle s}$ ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {P}}}$

     // Bedingung_L1: P+C+S+D schwarz
     // Transformation_L1:
     S->color = RED;
     // Fortsetzung der Überprüfung des Baums
     //   eine Ebene höher durch Testen auf die
     // Bedingung_L0:
    } while (--pParent >= &Parents[0])
    // Ende der (do while)-Schleife.

Delete case L0: The problem node (here:) is the root. ${\displaystyle {\mathsf {P}}}$

In this case you are done, since all paths lead through (and thus all paths contain one less black node than before). The black height of the tree is therefore reduced by 1. ${\displaystyle {\mathsf {P}}}$

   // Bedingung_L0: pParent < &Parents[0]
   //               ===> P ist die alte und neue Wurzel des Baums T.
   return; // Löschung fertiggestellt

${\displaystyle \scriptstyle n=1,}$

Iteration level ${\displaystyle \scriptstyle n\geqslant 2}$

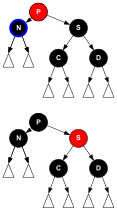
Delete case L2: The sibling of the problem node is red. ${\displaystyle {\mathsf {S}}}$ ${\displaystyle {\mathsf {N}}}$

A rotation around makes the grandparent of and a left rotation if the left child (i.e. ) is, otherwise a right rotation . (In the following, such a rotation is referred to as -rotation .) Then the colors of and are inverted. All paths still have the same number of black nodes, but now has a black sibling and a red parent, which is why we now turn to cases L3, L4 or L5 can continue - with the old and new problem nodes. ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {S}}}$ ${\displaystyle {\mathsf {N}},}$ ${\displaystyle {\mathsf {N}}}$d == LEFTd ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {S}}.}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {C}},}$ ${\displaystyle {\mathsf {P}},}$ ${\displaystyle {\mathsf {N}}}$

 Fall_L2:
   // Bedingung_L2: S rot && P+C+D schwarz
   // Transformation_L2:
   S->color = BLACK;
   P->color = RED;
   C = S->child[d];  // aufbewahren
   // rotate(P,d);   // d-Rotation um Knoten P:
   P->child[!d] = C; // neuer Elter von C
   S->child[d] = P;
   if (--pParent >= &Parents[0])
    {
     // Ersetze P bei seinem Elter durch S:
     R = *pParent;
     R->child[P == R->right] = S;
    }
   else // P war die Wurzel
     T->root = S; // S ist die neue Wurzel
 
   // Neuzuweisung nach der Transformation:
   S = C; // neues Geschwister von N (schwarz)
   if (((D = S->child[!d]) != NULL) && (D->color == RED))
     goto Fall_L5; // der ferne Neffe D ist rot
   if (((C = S->child[ d]) != NULL) && (C->color == RED))
     goto Fall_L4; // der nahe  Neffe C ist rot
   // Beide Neffen sind == NULL (erste Iteration)
   //   oder schwarz (später).
   // Also P rot && C+S+D schwarz <==> Bedingung_L3.
   // Das ist Fall_L3:

${\displaystyle \scriptstyle n=1,}$

Iteration level ${\displaystyle \scriptstyle n\geqslant 2}$

Clear case L3: The parent of is red, but both siblings of the problem node and its children and are black, if they exist. ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {S}}}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {C}}}$ ${\displaystyle {\mathsf {D}}}$

Inverting the colors of and leaves the number of black nodes on the paths that run through unchanged, but adds a black node to all paths and thus compensates for the missing black nodes on these paths. ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {S}}}$ ${\displaystyle {\mathsf {S}}}$ ${\displaystyle {\mathsf {N}}}$

 Fall_L3:
   // Bedingung_L3: P rot && C+S+D schwarz
   // Transformation_L3:
   S->color = RED;
   P->color = BLACK;
   return; // Löschung fertiggestellt

${\displaystyle \scriptstyle n=1,}$

Iteration level ${\displaystyle \scriptstyle n\geqslant 2}$

Delete case L4: The sibling of is black, the near nephew is red, while the distant nephew, if he exists, is black. The node shown in red and black in the diagram keeps its color, red or black. ${\displaystyle {\mathsf {S}}}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {C}}}$ ${\displaystyle {\mathsf {D}},}$ ${\displaystyle {\mathsf {P}}}$

A (non- d) rotation around makes the parent of and at the same time the sibling of Afterwards, the colors of and are inverted . This changes the paths of the subtree so that they lead through one less red node and the paths through the node through one more . However, the number of black nodes on these paths remains the same. Furthermore, there is now a black sibling whose distant child is red, with which one can move on to case L5. Neither nor the black height are influenced by this transformation. ${\displaystyle {\mathsf {S}}}$ ${\displaystyle {\mathsf {C}}}$ ${\displaystyle {\mathsf {S}}}$ ${\displaystyle {\mathsf {N}}.}$ ${\displaystyle {\mathsf {S}}}$ ${\displaystyle {\mathsf {C}}.}$ ${\displaystyle {\mathsf {2}}}$ ${\displaystyle {\mathsf {D}}}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {C}},}$ ${\displaystyle {\mathsf {S}},}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {P}}}$

 Fall_L4:
   // Bedingung_L4: S+D schwarz && C rot
   // Transformation_L4:
   // rotate(S,!d); // (nicht-d)-Rotation um Knoten S:
   S->child[d] = C->child[!d]; // neuer Elter für Teilbaum 3
   C->child[!d] = S;
     // dadurch wird S zum fernen Neffen von N
   P->child[!d] = C;
   C->color = BLACK;
   S->color = RED;
 
   // Neuzuweisung nach der Transformation:
   D = S; // neuer ferner Neffe
   S = C; // naher Neffe wird neues Geschwister von N
   // Weiter zu Fall_L5:

${\displaystyle \scriptstyle n=1,}$

Iteration level ${\displaystyle \scriptstyle n\geqslant 2}$

Delete case L5: The parent can be of any color . The sibling of is black and the distant nephew of is red. ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {S}}}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {D}}}$ ${\displaystyle {\mathsf {N}}}$

A d-Rotation to make the grandparent of now, it is enough , the color of give and and black coloring. still has the same color, which means that the ! RR requirement remains fulfilled. But now has an additional black ancestor: If before the transformation was not black, it is black after the transformation, and if was black, as has now a black grandparent why the paths that lead, now an additional black Knot happen. ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {S}}}$ ${\displaystyle {\mathsf {N}}.}$ ${\displaystyle {\mathsf {S}}}$ ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {D}}}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {S}}}$ ${\displaystyle {\mathsf {N}}}$

There are two options for the paths that change and that do not lead through : ${\displaystyle {\mathsf {N}}}$

1. The path leads through the arbitrarily colored root of the subtree that will become the new sibling of . Then the path must lead through and lead both before and after the transformation . Since the two nodes have only swapped their colors, the number of black nodes on the path does not change. ${\displaystyle {\mathsf {3}}}$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {S}}}$ ${\displaystyle {\mathsf {P}}}$
2. The path leads through the new uncle of whom the (non- ) child of the sibling is. In this case the path previously carried out and . After the transformation, however, it only leads through the one that was colored from red to black (the previous color of ) and the node that has taken the color of . Thus, the number of black nodes in such a path does not change. ${\displaystyle {\mathsf {D}}}$ ${\displaystyle {\mathsf {N}},}$d ${\displaystyle {\mathsf {S}}}$ ${\displaystyle {\mathsf {D}},{\mathsf {S}}}$ ${\displaystyle {\mathsf {P}}}$ ${\displaystyle {\mathsf {D}},}$ ${\displaystyle {\mathsf {S}}}$ ${\displaystyle {\mathsf {S}},}$ ${\displaystyle {\mathsf {P}}}$

Since the number of black nodes in the paths that lead through increases by 1, and in those that do not lead through does not change, the requirement S # = is restored. ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {N}}}$

 Fall_L5:
   // Bedingung_L5: S schwarz && D rot
   // Transformation_L5:
   // rotate(P,d); // d-Rotation um Knoten P:
   P->child[!d] = S->child[d];    // neuer Elter für Teilbaum 3
   S->child[d] = P;
   if (--pParent >= &Parents[0])  // P war nicht die Wurzel
    {
     // Ersetze P bei seinem Elter durch S:
     N = *pParent;
     N->child[P == N->right] = S;
    }
   else
     T->root = S; // S ist die neue Wurzel
 
   S->color = P->color;
   P->color = BLACK;
   S->child[!d]->color = BLACK; // im Diagramm: D
   return; // Löschung fertiggestellt
  } // Ende RBdelete2

Operations with whole red-black trees

The following two operations have whole red-black trees as input and output operands. They are not part of the standard set and are missing in some implementations. However, it should be shown here that they can also be carried out with a logarithmic effort.

Concatenation (join)

Concatenation of 2 red-black trees

The operation concatenates (English: join or concat ) two red-black trees using a single key with logarithmic effort. For the sorting sequence, of course, all keys of the first tree must precede the single key and this must precede all keys of the second . The in-order traversal of the chained tree is equivalent to performing the traversal of the first tree in sequence, followed by that of the single node, followed by that of the second tree. JOIN(TL,k,TR)TLkTR

Sketch of the algorithm:
Without loss of generality, the first tree is not lower than the second, and the second has a black root (node in the figure) of the black height . Furthermore, the first element is already taken from the second tree . It then plays the role of a “link”. One descends on the right flank of the first tree to a black knot of the black height, be his name . The knot is colored red and made to the right child of the parent of . If black, then the linked tree is in red-black form and the link is complete. However, if red, then his left child is black. A repair loop can now be connected, which has the same invariant as the insert operation, ascending towards the root, and is the problem node of the first iteration level. ${\displaystyle {\mathsf {H}}}$ ${\displaystyle s}$ ${\displaystyle {\mathsf {G}}}$
${\displaystyle s}$ ${\displaystyle {\mathsf {F}}}$ ${\displaystyle {\mathsf {G}}}$ ${\displaystyle {\mathsf {E}}}$ ${\displaystyle {\mathsf {F}}}$ ${\displaystyle {\mathsf {E}}}$ ${\displaystyle {\mathsf {E}}}$ ${\displaystyle {\mathsf {G}}}$

Bulk operations

Based on the JOIN operation, further mass and quantity operations can be created, all of which have logarithmic runtimes, e.g. B. the complementary operation of splitting (English: split ) a tree on a path.

The bulk deletion of all keys in a coherent area (interval) can be done by splitting twice and concatenating them once or, if the smallest or largest element is included, splitting once. In a similar way, an interval can be prepared from a red-black tree as a red-black tree with logarithmic effort.

A mass insertion can be carried out by splitting once and concatenating twice, provided the set is prepared as a red-black tree and its keys are in an interval that does not occur in the target tree.

Set operations

In the same article it was shown that the set operations average , union and difference of digitally represented (finite) sets can be implemented very efficiently (in logarithmic time) and in “natural” parallelism (see binary search tree # building efficient mass and set operations on the JOIN operation ). Blelloch et. al. show that these algorithms can be transferred to the 4 balanced search trees (AVL-, Red-Black-, Splay- and BB [α]) in such a way that everything specific takes place in the JOIN algorithm.

Height proof

As already stated in the introduction, the special property of red-black trees is that they can search , delete or insert an element in the tree in logarithmic time - more precisely in with than the number of keys . These operations are dependent on the height of the tree on all binary search trees . The lower the height of the tree, the faster the operations run. If one can now prove that a binary search tree with elements never exceeds a certain height (in the case of the red-black tree ), then it has been proven that the operations mentioned above have logarithmic costs in the worst case, namely the costs of for a tree in which items are stored. ${\displaystyle {\mathcal {O}}(\log n)}$ ${\displaystyle n}$ ${\displaystyle h}$ ${\displaystyle n}$ ${\displaystyle 2\log _{2}(n\!+\!2)\!\!-\!\!2}$ ${\displaystyle 2\log _{2}(n\!+\!2)\!\!-\!\!2}$ ${\displaystyle n}$

Red-black trees with the smallest number of nodes for a given height

Red-black trees RB _h of heights h = 1,2,3,4,5,
each with a minimum number of nodes 1,2,4,6 resp. 10.

Too there is a red-black tree of height with ${\displaystyle h\geq 0}$ ${\displaystyle h}$

${\displaystyle m_{h}=2^{\lfloor (h+1)/2\rfloor }+2^{\lfloor h/2\rfloor }-2}$

Knots, and none with less ( stands for the Gaussian bracket ). ${\displaystyle \lfloor \,\rfloor }$

proof

In order for a red-black tree of a certain height to have a minimum number of nodes , it must contain exactly one longest path, and this has the largest possible number of red nodes in order to achieve the largest possible tree height with the smallest possible black height. Its coloring must therefore begin with red at the bottom of the leaf and then continue up to the root with black and red, strictly alternating. Outside this path that defines the height of the tree, it has only black nodes. Assuming there is a red node there, removing it does not affect the red-black properties, provided that one of its two (black) child nodes moves up in its place and the other, including its subtree, is removed at the same time. All subtrees outside the longest path are therefore complete binary trees with exclusively black nodes. ${\displaystyle h}$

There is exactly one red-black tree of height with a red leaf, which is also the root. So is in accordance with ${\displaystyle h=1}$ ${\displaystyle m_{1}=1}$ ${\displaystyle 2^{\lfloor (1+1)/2\rfloor }\!+\!2^{\lfloor 1/2\rfloor }\!\!-\!\!2=2^{1}\!+\!2^{0}\!\!-\!\!2.}$

For a minimum tree (RB _h in the figure) of height , the two child trees of the root are of different heights: the higher one contains the longest path defining the height and is a minimum tree of height with nodes and black height ; the lower one is a complete binary tree with height = black height so has nodes. So it's recursive ${\displaystyle h>1}$ ${\displaystyle h\!\!-\!\!1}$ ${\displaystyle m_{h-1}}$ ${\displaystyle s:=\lfloor (h\!\!-\!\!1)/2\rfloor }$ ${\displaystyle s,}$ ${\displaystyle 2^{s}\!\!-\!\!1=2^{\lfloor (h-1)/2\rfloor }\!\!-\!\!1}$

	${\displaystyle m_{h}}$	${\displaystyle =}$	${\displaystyle (m_{h-1})}$		${\displaystyle +}$	${\displaystyle (1)}$	${\displaystyle +}$	${\displaystyle (2^{\lfloor (h-1)/2\rfloor }-1)}$
			(large child tree)			(Root)		(small child tree)
what one
	${\displaystyle m_{h}}$	${\displaystyle =}$	${\displaystyle (2^{\lfloor h/2\rfloor }+2^{\lfloor (h-1)/2\rfloor }-2)}$				${\displaystyle +}$	${\displaystyle 2^{\lfloor (h-1)/2\rfloor }}$
		${\displaystyle =}$	${\displaystyle 2^{\lfloor h/2\rfloor }+2^{\lfloor (h+1)/2\rfloor }-2}$

calculates. ■

The graph of the function is convex downwards and piecewise linear with the corners at the points with Further, A027383 ( h -1) for with the sequence A027383 in OEIS . ${\displaystyle m_{h}}$ ${\displaystyle (h=2k\;|\;m_{h}=2^{k+1}\!\!-\!\!2)}$ ${\displaystyle k\in \mathbb {N} .}$ ${\displaystyle m_{h}=}$ ${\displaystyle h\geq 1}$

There are forms of minimal trees for the height , since the position of the longest path corresponds to the position of an external leaf of the complete binary tree of the height and this also determines the position of the nodes outside of this path. (The illustration shows the leftmost position.) ${\displaystyle h}$ ${\displaystyle 2^{h-1}}$ ${\displaystyle h\!\!-\!\!1}$

Reshaping

Because of (a sequence of ) we have the inequality for odd ${\displaystyle 3>2^{\tfrac {3}{2}}}$ ${\displaystyle 9>8}$ ${\displaystyle h}$

${\displaystyle m_{h}=3\cdot 2^{\tfrac {h-1}{2}}-2=3\cdot 2^{-{\tfrac {3}{2}}}\cdot 2^{\tfrac {h+2}{2}}-2>2\cdot 2^{\tfrac {h}{2}}-2,}$

so that for everyone (even and odd) ${\displaystyle h}$

${\displaystyle m_{h}\geq 2\cdot 2^{\tfrac {h}{2}}-2}$

results.

Since the smallest number of nodes for all red-black trees is the height , the following applies: ${\displaystyle m_{h}}$ ${\displaystyle n}$ ${\displaystyle h}$

${\displaystyle 2\cdot 2^{\tfrac {h}{2}}-2\leq m_{h}\leq n.}$

If you now bring the summand –2 to the right-hand side and logarithmically, it follows:

${\displaystyle {\begin{matrix}&2\cdot 2^{\tfrac {h}{2}}-2&\leq &n\\\Longleftrightarrow &2\cdot 2^{\tfrac {h}{2}}&\leq &n+2\\\Longleftrightarrow &1+{\tfrac {h}{2}}&\leq &\log _{2}(n+2)\\\Longleftrightarrow &{\tfrac {h}{2}}&\leq &\log _{2}(n+2)-1\\\Longleftrightarrow &h&\leq &2\log _{2}(n+2)-2\\\end{matrix}}}$

Hence the assertion that a red-black tree has a maximum height of and can therefore search , insert and delete operations in logarithmic time. Expressing this result in the O notation , so results for the cost of the above operations that they all are with than the number of keys. ${\displaystyle h}$ ${\displaystyle 2\log _{2}(n\!+\!2)\!\!-\!\!2}$ ${\displaystyle {\mathcal {O}}(\log n)}$ ${\displaystyle n}$

Average and amortized term

The red-black tree offers amortized constant rebalancing costs and thus constant on average .

Applications of (binary) search trees, which in addition to sequences of insertions and deletions also contain search operations, are asymptotically dominated by the logarithmic runtime of the latter. The amortized constant modification effort is interesting, however, if the search tree is to be kept persistent , i.e. H. all versions should remain accessible (see also  en: Persistent data structure ).

Numbers of red-black trees

The sequence A001131 in OEIS gives the total number of red-black trees depending on the number of nodes , sequence A001137 in OEIS those with black roots and sequence A001138 in OEIS those with red roots. ${\displaystyle (n\!+\!1)}$ ${\displaystyle n}$

The 3 RB trees with 3 keys

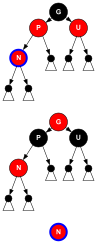
The figure on the right shows the balanced binary tree with 3 keys in 3 different red-black colors that conform to the rules. When searching and traversing , all behavior including runtime is the same because of the identical branches of the 3 trees. However, there are differences in the case of modifications, e.g. in the case of insertions: In the case of the left coloring, all the insertions are of the type Transformation_E2 followed by Transformation_E0, in the case of the right 2 coloring all are of the type Transformation_E1.

In a pure insertion scenario, of the 3 possible trees with 3 nodes (keys), only one tree with a black root and 2 red children (the one on the left in the figure) is formed. However, if deletions are included, then the two other red-black trees (on the right in the figure) are added,

namely the one with the red root above

4 insertions and 1 deletion

and the one with black root over

6 insertions and 3 deletions

and this with the algorithms for insertion and deletion described above - in each case with a suitably selected key sequence, which is indicated by the node with the blue outline.

Relationship to 2-3-4 trees

2 children

3 children

3 children

4 children

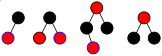
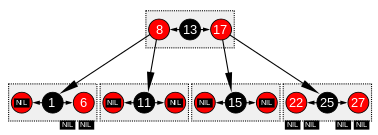
The 4 small graphics on the left and right show how small building blocks of a red-black tree (left halves of the graphics) can be matched with a (thick) knot of a 2-3-4 tree (right halves of the graphics). A 2-3-4 tree is created from a red-black tree by including red children on the left or right as data elements in the black parent node according to their child direction.

The red-black tree of the example represented as a 2-3-4 tree

Conversely, a 2-3-4 tree can easily be converted into a red-black tree: A node with 2 data elements and 3 child pointers (like the node [NIL, 1,6] in the figure) becomes a black node (Data element) with 1 child pointer and a red child node (data element) that still contains 2 child pointers; a node with 3 data elements and 4 child pointers (like nodes [8,13,17] and [22,25,27] in the figure) becomes a black node (data element) with 2 red child nodes (each 1 data element and 2 child pointers ).

Moreover, there are correspondences with the modification operations (insert, delete) between color changes and rotations on the side of red-black trees and the Actions column ( English split ) and fusion ( English fuse ) in the 2-3-4 trees.

In contrast to 2-3-4 trees, with red-black trees you do not have to monitor and manage the " fill level " (memory utilization, English fill factor ) of the nodes, which is why the latter is a very efficient way of implementing the 2-3-4 -Trees apply.

Comparison with AVL tree

The set of AVL trees is a real subset of the set of red-black trees. Because every binary tree that fulfills the AVL criterion can be colored in a way that fulfills the red-black criterion .

Red-black, but not AVL tree

But there are red-black trees that do not meet the AVL criterion. The figure opposite shows, for example, a red-black tree with 6 nodes and the external path length sum 21, while 20 is the largest external path length sum for AVL trees (and at the same time the smallest possible for all binary trees) of this number of nodes. Consequently, the worst-case height of the AVL tree is also smaller than that of the red-black tree, asymptotically by the factor (2 log ₂ Φ ) ⁻¹ ≈ 0.720. In general, AVL trees are viewed as better balanced and their search behavior as more favorable.

The runtimes for all the operations listed differ on average and in the worst case asymptotically only by a constant factor, i.e. they belong to the same complexity class . The red-black tree, however, offers amortized constant insertion and deletion costs (only rebalancing in each case - without navigation). With the AVL tree, only the insertion costs are amortized, the deletion costs remain constant on average .

Realistic application situations with performance data and comparisons - also with other search algorithms and types of data structures - can be found at Ben Pfaff . In 79 measurements, his results show, among other things, the very great similarity of AVL trees ( AVL ) and red-black trees ( RB ) with runtime ratios ^AVL ⁄ _RB between 0.677 and 1.077 with a median of ≈ 0.947 and a geometric mean of ≈ 0.910 .

The storage space requirements are practically identical: 1 bit for the red-black attribute versus 2 bits for the AVL balance factor. While the balance factors of an AVL tree depend directly on its (graph-theoretical) shape, different colors are possible for red-black trees of the same shape - except for the minimum trees of straight height (see §  Numbers of red-black trees ) . The differences in coloration only affect the modification and not the navigation operations. Furthermore, every possible shape of an AVL tree can also be created through specific insertions. In relation to the tree shape, this also applies to red-black trees; There are, however, tree shapes for which coloring that conforms to the rules cannot be effected in a pure insertion scenario.

One consequence of this somewhat greater degree of freedom is that in the red-black tree, the color changes and rotations required for inserting or deleting can already be made during the search process - i.e. when descending. This "top-down strategy" is of interest , for example, for concurrent and persistent programming .

The newly inserted node remains red when you insert it. This means that an associated search function in the descent can prepare the tree along the path concerned (in logarithmic time) in such a way that the final insertion takes place directly in the case of a black parent in the form of a red knot or even (after an inspection of the parent, if necessary) can be omitted. Likewise, when deleting a (different) search function can prepare the tree in the descent so that the node to be deleted is red. In both cases, the tree remains a valid red-black tree, both when the modification is carried out and when it is omitted, a modification that only consists of setting a single pointer when inserted and is only slightly more complicated when deleted. In contrast, there are tree forms in the AVL tree in which the decision regarding the implementation of the modification cannot be kept open with such little implication.

Use of red and black trees

In the Java Development Kit , the classes TreeSetand are implemented TreeMapas red-black trees. They provide ordered sets or ordered dictionaries .

More trees

• 2-3-4 tree
• AVL tree
• B-tree
• Heap (data structure)
• Search tree

literature

• Ben Pfaff: An Introduction to Binary Search Trees and Balanced Trees. Free Software Foundation, Boston 2004, ftp.gnu.org (PDF gzip; 1662 kB; accessed January 13, 2019).
• Ben Pfaff: Performance Analysis of BSTs in System Software. Stanford University, 2004, stanford.edu (PDF; 316 kB).
• Thomas H. Cormen, Charles E. Leiserson , Ronald L. Rivest , Clifford Stein: Introduction to Algorithms . 2nd Edition. MIT Press, Cambridge (Massachusetts) 2001, ISBN 0-262-03293-7 , pp. 273-301 .
• Robert Sedgewick : Algorithms in C ++ . Addison-Wesley, 1992, ISBN 3-89319-462-2 , pp. 260-270 (English).
• Robert Sedgewick , Kevin Wayne: Algorithms Fourth Edition. Pearson Education, 2011, ISBN 978-0-321-57351-3 , pp. 432-447.
• Andrew Binstock, Jon Rex: Practical Algorithms for Programmers. Addison-Wesley Professional, 1995, ISBN 0-201-63208-X .
• Kurt Mehlhorn: data structures and efficient algorithms. Teubner Stuttgart 1988, ISBN 3-519-12255-3 .
• Kurt Mehlhorn , Peter Sanders : Algorithms and Data Structures. The Basic Toolbox . Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-77977-3 , doi : 10.1007 / 978-3-540-77978-0 .
• Roger Whitney (San Diego State University): CS 660: Red – Black tree notes
• Mathworld: Red – Black Tree

Web links

• Java applet for the operation of a red-black tree
• Term paper on the topic of red-black trees

Individual evidence

1. ^ Rudolf Bayer : Symmetric Binary B-Trees. Data Structure and Maintenance Algorithms . In: Acta Informatica . 1, 1972, pp. 290-306. doi : 10.1007 / BF00289509 .
2. ^ Leo J. Guibas, Robert Sedgewick: A Dichromatic Framework for Balanced Trees . In: IEEE Computer Society (Ed.): Proceedings of the 19th Annual Symposium on Foundations of Computer Science . 1978, pp. 8-21.
3. ↑ The text follows Ben Pfaff: An Introduction to Binary Search Trees and Balanced Trees . For other variants of the requirements see the comment NIL node .
4. ↑ at Ben Pfaff non-branching node
5. ↑ For Ben Pfaff , the black level of a node is the uniform number of black nodes on all paths to the path ends in the subtree rooted by him.
6. ↑ Mehlhorn 2008 S. 155 colors the edges red / black and counts as Black Depth ( English black depth ) of a node, the number of black edges from it to the root.
7. ↑ ^{a b} Some authors still demand that the root of the tree should be colored black. But not z. B. Mehlhorn 2008 and Sedgewick . In fact, this requirement has no mathematical meaning and disturbs the recursiveness . Because if the root is red, your children must be black according to demand ! RR , and if they are changed to black none of the other demands are violated. In the algorithms for insertion and deletion, however, it is not possible to make do with a case distinction if one can always assume a parent node for a red node .
8. ^ ^{A b} J. R. Driscoll, N. Sarnak, DD Sleator, RE Tarjan: Making Data Structures Persistent. In: Journal of Computer and System Sciences. Volume 38, No. 1, 1989 ( cs.cmu.edu )
9. ^ Thomas H. Cormen, Charles E. Leiserson , Ronald L. Rivest , Clifford Stein: Introduction to Algorithms . 2nd Edition. MIT Press, Cambridge (Massachusetts) 2001, ISBN 0-262-03293-7 , pp. 273 .
10. ↑ where is       key of <key of . S. a. Binary search tree # Search if duplicates are allowed .d == LEFT       ${\displaystyle \Longleftrightarrow }$ ${\displaystyle {\mathsf {N}}}$ ${\displaystyle {\mathsf {P}}}$
    
11. ↑ ^{a b In} this way (like Ben Pfaff - at least conceptually) , the implementation manages without a parent pointer stored in the node.
    For the size of such a stack see Stack size .
12. ↑ In addition to the variant of the text, Ben Pfaff also brings a variant with a first inserted black node.
13. ↑ The short form with the arrow ->is explained in the article Verbund (data type) .
14. ↑ This division can be found u. a. with Ben Pfaff .
15. ↑ ^{a b} Another possibility is to add the loop body to the do whileloop in two versions, one for the child direction on the left and one for the right (e.g. Ben Pfaff ).
16. ↑ ^{a b} For the advantages of iterative programming in terms of space and time compared to recursive programming, see chap. a. Binary search tree # Iterative programming . In addition, the former forces a closer attention to the knot properties.
17. ↑ This approach was first suggested by T. Hibbard in 1962, quoted from Robert Sedgewick , Kevin Wayne: Algorithms Fourth Edition. Pearson Education, 2011, ISBN 978-0-321-57351-3 , p. 410 (accessed March 25, 2018)
18. ↑ The division corresponds to Roger Whitney .
19. ↑ The University of Science and Technology of China (quoted from stackoverflow.com ) comes up with a different division (of the conditions) of the cases, but also in the result to the total number 6 .
20. ^ Robert Endre Tarjan: 4. Search Trees 5. Linking and Cutting Trees . In: SIAM (=  Data structures and network algorithms ). 1983, ISBN 978-0-89871-187-5 , pp. 45-70 , doi : 10.1137 / 1.9781611970265.ch5 .
21. ^ Donald E. Knuth: The Art of Computer Programming , Volume 3, Sorting and Searching, 2nd Edition, Addison-Wesley, 1998, p. 474
22. ↑ Guy Edward Blelloch, Daniel Ferizovic, Yihan Sun: Just Join for Parallel Ordered Sets . Ed .: ACM (=  Symposium on Parallel Algorithms and Architectures, Proc. Of 28th ACM Symp.Parallel Algorithms and Architectures (SPAA 2016) ). 2016, ISBN 978-1-4503-4210-0 , pp. 253-264 , doi : 10.1145 / 2935764.2935768 , arxiv : 1602.02120 . .
23. ↑ Sedgewick 2011 p. 444 Proof sketch
24. ↑ Mehlhorn and Sanders dedicate the chapter "7.4 Amortized Analysis of Update Operations" with theorem 7.3, p. 158 to this topic in Mehlhorn 2008 :

    " Consider an (a, b) -tree with b ≥ 2a that is initially empty. For any sequence of n insert or remove operations, the total number of split or fuse operations is O (n). "

    Translated into the language of the red-black trees this means:

    For any sequence of insert and delete operations in an initially empty red-black tree, the number of color changes and rotations is in ${\displaystyle n}$ ${\displaystyle {\mathcal {O}}(n).}$

    The effort per operation in such a sequence is therefore constant in an amortized manner. In the proof that is given for (2,4) trees and in which the account method comes into play, only the split and fuse operations are billed - a visit to the affected location in the tree is neither mentioned nor mentioned counted in. The statement therefore relates to the pure repair costs. ${\displaystyle {\mathcal {O}}(1),}$
25. ^ Lightweight Java implementation of Persistent Red-Black Trees
26. ↑ Mehlhorn 1988 p. 193
27. ↑ If the two options (eg. On the first upper) in 3 children in a limiting, one comes to the LLRB (abbreviation for English left-leaning red-black ) trees, which have substantially the same information-theoretic properties, wherein whose implementation, however, according to Sedgewick, can be distinguished from fewer cases (see  Robert Sedgewick. Left-leaning Red – Black Trees and PDF ).
28. ↑ Mehlhorn 1988 p. 187
29. ^ Paul E. Black: Red-black tree. In: Dictionary of Algorithms and Data Structures . National Institute of Standards and Technology , April 13, 2015, accessed July 2, 2016 . 
30. ↑ s. " One should be able to color any AVL tree, without restructuring or rotation, to transform it into a Red-Black tree. “Junghyun Chae in AVL Trees vs. Red-Black Trees? Retrieved October 14, 2015 and proof in AVL tree # ComparisonRB .
31. ↑ Red Black Trees . Retrieved October 14, 2015. (Eternally Confuzzled)
32. ↑ Mehlhorn 1988 pp. 197-198.
33. ↑ s. a. Comparison of Binary Search Trees, accessed October 14, 2015; or Paul Callahan in AVL Trees vs. Red-Black Trees? accessed on October 14, 2015
34. ↑ Java Class TreeSet on docs.oracle.com
35. ↑ Java Class TreeMap on docs.oracle.com

Remarks

1. ↑ This estimate is sharp (see §  Height proof ) and for because of ${\displaystyle n>0}$

   ${\displaystyle {\begin{matrix}&{\tfrac {n}{2}}&<&n\\\Longleftrightarrow &{\tfrac {n+2}{2}}&<&n+1\\\Longleftrightarrow &\log _{2}(n+2)-1&<&\log _{2}(n+1)\\\Longleftrightarrow &2\log _{2}(n+2)-2&<&2\log _{2}(n+1)\end{matrix}}}$

   marginally more accurate than

   ${\displaystyle 2\log _{2}(n+1)}$.

2. ↑ If the NIL nodes are implemented as minimal red-black nodes, they need memory for two child pointers, possibly a parent pointer, the field for the color and a recognition field for the »NIL node« property. In key-bearing nodes you need NIL nodes, bringing the red-black overhead more than doubled. The links between the NIL nodes and the nodes carrying the key (e.g. for the rotations) must also be maintained so that the running time is extended. As a result, this means a considerable effort for recording and maintaining information that is not needed for the subsequent algorithms or that can be derived directly from the other information. ${\displaystyle n}$ ${\displaystyle n\!+\!1}$
3. ↑ ^{a b c} Note the type of evaluation of the specified in the C programming language

   	Disjunction:	(X == NULL)
   		|| (X->color == BLACK)
   or the
   	Conjunction:	(X != NULL)
   		&& (X->color == RED)

   which in the case of X == NULLthe second condition X->color == BLACKrespectively. X->color == RED does not evaluate, but branches immediately to the elsebranch . In the example code, the corresponding lines are highlighted in yellow.
   Additional remark:
   The black level 0 only occurs in the first iteration level of the repair loop; at the higher iteration levels the black level of all visited nodes is positive, thus also (X != NULL)- and this part of the query can be omitted.
   On the other hand, if one knows that the black level of a node is 0, then if it exists it can only be red. If the first iteration is now pulled out of the loop, the query there can be (X != NULL)limited to, whereas with the higher iteration levels only has to be colorqueried.

4. ↑ ^{a b c d} In the first iteration level, the subtree is empty. If the nodes are implemented with a parent pointer, then the parent pointer of this subtree must be adapted at all iteration levels except the first after the rotation. ${\displaystyle {\mathsf {3}}}$
5. ↑ Because of the equations LEFT ≡ 0 and RIGHT ≡ 1reflects the logical negation

   Not-d   ≡   !d   ≡   (1−d)

   the direction . It is the child's sense of . In the context of colors, one speaks of “inversion” when assigning a la and .LEFT ${\displaystyle \longleftrightarrow }$ RIGHTd = (N == P->right)N
RED :≡ !BLACKBLACK :≡ !RED
6. ↑ For the sake of brevity, the example gotocode is used a few times . It is easy to avoid this by duplicating the code.
7. ↑ If the nodes are implemented with a parent pointer, then the parent pointer of the node must be adapted in all iterations, since the black level of is ≥ 1 in the first iteration as well. ${\displaystyle {\mathsf {C}}}$ ${\displaystyle {\mathsf {C}}}$
8. ↑ These minimal trees play a similar role in the red-black trees as the Fibonacci trees in the AVL trees.
9. ↑ As a data structure that is accommodated in the homogeneous working memory (main memory), the size of the red-black tree is limited, including the height of the tree and the lengths of the paths from leaf to root. The programmer will limit the number of nodes to his users rather than the tree height, which for the user is more of a random nature and normally does not interest him.
   The following table returns a height specification for each node number that is not exceeded by a red-black tree with elements. Main memories with 32-bit and 64-bit wide virtual 8-bit byte addresses are common. Since a maximum of bytes can be accommodated in a 32-bit address space and a node requires at least 2 child pointers of 4 bytes each, a tree with a maximum of nodes can be accommodated for user data (key + value) of bytes per node ; when these are As the table shows, in 32-bit address space, the height may be exceeded impossible by a red-black tree. For an address space with 8-byte addresses and byte user data you have so that remains and the use of these can not overflow bytes for the parent stack. ${\displaystyle n}$ ${\displaystyle h}$ ${\displaystyle \leq n}$ ${\displaystyle 2^{32}}$ ${\displaystyle b}$ ${\displaystyle n=2^{32}/(2\cdot 4\!+\!b)}$ ${\displaystyle b=3}$ ${\displaystyle n=390451572.}$ ${\displaystyle h=55}$
   ${\displaystyle b=1}$ ${\displaystyle n\leq 2^{64}/(2\cdot 8\!+\!b)}$ ${\displaystyle =1085102592571150095,}$ ${\displaystyle h\leq 117}$ ${\displaystyle 8h=8\cdot 117=936}$

   Scope of red-black trees

   	Number of nodes ${\displaystyle n\leq }$	Tree height ${\displaystyle h\leq }$	Usable length ${\displaystyle b\leq }$
   32-bit addresses	⋮	⋮	⋮
   	33554429	47	120
   	50331645	48	77
   	67108861	49	56
   	100663293	50	34
   	134217725	51	24
   	201326589	52	13
   	268435453	53	8th
   	402653181	54	2
   	536870909	55	0
   64-bit addresses	⋮	⋮	⋮
   	72057594037927933	109	240
   	108086391056891901	110	154
   	144115188075855869	111	112
   	216172782113783805	112	69
   	288230376151711741	113	48
   	432345564227567613	114	26th
   	576460752303423485	115	16
   	864691128455135229	116	5
   	1152921504606846973	117	0

   With the designations in the text is a requirement that remains as close as possible below the number of nodes of the next largest minimal tree. If the memory requirements are the same for all nodes, the maximum user data per node can be ${\displaystyle n=m_{h+1}-1,}$

   ${\displaystyle b={\begin{cases}\\\\\end{cases}}}$	${\displaystyle 2^{32}/n-2\cdot 4}$		in the 32-bit address space (4 bytes / address)
   	${\displaystyle 2^{64}/n-2\cdot 8}$		in the 64-bit address space (8 bytes / address)

   Bytes include.

   Conclusion

   If the stack memory struct node* Parents[] for the parent pointers in a 32-bit address space is designed for at least entries with a total of bytes, it cannot possibly overflow. The same applies to a 64-bit address space for and a parent stack of bytes in size . Before the parent stack overflows in both cases, the address space has already burst. Ben Pfaff has . ${\displaystyle h=54}$ ${\displaystyle 4h=4\cdot 54=216}$
   ${\displaystyle h=117}$ ${\displaystyle 8h=8\cdot 117=936}$
   
   #define RB_MAX_HEIGHT 128

10. ↑ or only 1 bit (see  AVL implementation )
11. ↑ The locks that serve to maintain the consistency of a tree that is subject to change can be set in the top-down strategy from the roots to the leaves. If all processes working on the tree adhere to such (and possibly other) protocols, a deadlock can be avoided.

This version was added to the list of articles worth reading on November 5, 2005 .