Binary search tree
In computer science , a binary search tree is a combination of the abstract data structures search tree and binary tree . A binary search tree, often abbreviated as BST (from English Binary Search Tree ), is a binary tree in which the nodes have "keys" and the keys of the left subtree of a node are only smaller (or equal) and those of the right subtree only are greater than (or equal to) the key of the node itself.
What the terms “less than or equal to” and “greater than or equal to” mean is entirely up to the user; they only have to establish a total order (more precisely: a total quasi-order see below ). The order relation is realized most flexibly by a 3-way comparison function provided by the user . It is also up to the user whether it is a single key field or a combination of fields; furthermore whether duplicates (different elements, which do not come out as "unequal" in the comparison) should be permitted or not. About search functions for this case see below .
An in-order run through a binary search tree is equivalent to walking through a sorted list (with essentially the same runtime behavior). In other words, a binary search tree has possibly considerably more functionality (for example, run in the opposite direction and / or a "direct access" with potentially logarithmic runtime behavior - achieved by the principle of "divide and rule" , which on the long-range effect of Transitivitätsgesetzes based ) with the same or only slightly higher memory requirements.
motivation
Search trees are solutions to the so-called "dictionary problem". Assume a large number of keys, each with a value. In a German – English dictionary, the German word is the key and English words are the searched value. The situation is similar with a telephone book with name and address as the key and the telephone number as the value you are looking for.
From a mathematical point of view, a dictionary implements a (finite) function with pairs (key, value). During the search, a search term (argument of the function) is matched with one of the keys. If this is successful, the added value is assigned to the search term as a function value.
In both examples the keys are usually sorted. This is very useful because it allows you to open the book in the middle and check whether the search term has been found. If it is not found and if it is, for example, alphabetically before the letter "K", you also know that you do not have to compare with "L", "M" or "Z" further back. The part that remains for investigation is always a coherent segment, which, like the whole book, is halved again at the beginning - and so on until it is found or until it can be determined that the search term does not appear.
This procedure is called "binary search" in computer science. It is simulated in an obvious way by the well-known search method " binary search in the array ". In terms of information theory, their behavior is optimal, namely logarithmic , more precisely: With keys, you only need a maximum of ( rounding function and rounding function ) comparisons.
In contrast to the binary search, with "sequential search" the search term must potentially be compared with all keys. (The input does not need to be sorted for this, however.) The difference between the two methods can be considerable: In a telephone book with entries, comparisons must be carried out on average during sequential searches . A binary search leads to the same result after a maximum of comparisons.
Changes, additions and exits in dictionaries and telephone books can be sporadic, in software systems they usually have to be reflected on immediately . Entrances and exits require data transports in an array, the effort of which is proportional to the length of the array, i.e. linear in . Such an effort completely destroys the efficiency of binary searching.
The procedure for binary searches can also be reproduced with a binary tree. The first key with which the search term is to be compared is placed in the root of the binary tree. The next key to be found when the comparison result is “smaller” is placed in the left child node and the key for “larger” is placed in the right child node accordingly. You continue like this until all keys are in the binary tree. (This turns the binary tree into a binary search tree.)
By removing the individual elements from the array, great flexibility is gained: The effort involved in inserting, allocating storage space and loading the fields with values, and deleting in order to return the storage space, is independent of the number of elements. In the case of the binary tree, however, a measure for the balance is lost that is given in the array by taking the mean value between two indices. In addition, a binary tree that was once excellently balanced can lose its balance due to insertions and deletions and in extreme cases, when each node only has one child node (instead of two), degenerates into a linear list - with the result that a search is equivalent to a sequential search.
The computer scientists have developed various balance criteria for binary trees. For most of them, the effort involved in finding, inserting, and deleting is logarithmic, albeit with different constant factors. Some solution principles for the problem of degeneracy in dynamic binary trees can be found in

root , 13 inner nodes (green and blue) and 14 outer nodes (red); the inner ones with the keys of Fig. 1A
terminology
The terms node and edge , the latter by definition as directed edge (or arc and arrow ), are adopted from the general graphs . If the direction is clear enough from the context, edge is enough .
In the case of directed graphs , a node can be assigned both an output degree and an input degree. Binary trees are usually viewed as out-trees . In such a rooted tree there is exactly one node with the degree of entry 0. It is called the root . All other nodes have entry level 1. The exit level is the number of child nodes and is limited to a maximum of 2 in the binary tree. Its order as an out-tree is therefore ≤ 2.
Nodes with degree of exit ≥ 1 are called internal (inner) nodes , those with degree of degree 0 are called leaves or external (outer) nodes . In the case of binary trees - and only there - the term half-leaf is occasionally used for a node with degree 1 (sometimes English: non-branching node ). Then a leaf is a double half leaf.
Different ways of speaking
Keys in the form of capital letters are assigned to the nodes of the binary tree in FIG. 1A. Since the in-order traversal follows their (alphabetical) sorting order, the tree is a binary search tree.
Fig. 1B shows the identical set of keys in another binary search tree, a search tree that contains explicit “NIL nodes” . Here only the internal nodes carry keys, whereas the external , the NIL nodes (also called external leaves ), act as placeholders for the intervals between the keys (for example in Fig. 3 ), i.e. as insertion points in the binary search tree. (The node with the key is an internal leaf here .) There are no nodes with degree 1. The keyless search tree consists of exactly one node that is both external and root. Since in this view the height of the (totally) empty tree (which is not a search tree) is defined as -1, so the keyless tree is assigned the height 0, the height terms match if in the view of Fig. 1A the empty and at the same time Keyless tree is assigned height 0 and a tree that consists of only one node is assigned height 1.
Node-oriented and sheet-oriented storage
If - as above and in Fig. 1A - the contents of the set are stored in the nodes and the external nodes are empty, the type of storage is called node-oriented . To express that they do not belong to the set, in this case the external nodes are referred to as external leaves for better differentiation . An external sheet represents an insertion point.
In the case of sheet-oriented storage, the contents of the set are stored in the sheets, and the nodes only represent signs for navigation, which may have little to do with the set's keys.
Disambiguation
Please note:
- The term “neighbor” (and “neighborhood” etc.) is used in this article (and with the search trees in general) differently than usual in graph theory , namely exclusively in the sense of the imprinted order relation: “right” neighbor means the next node in ascending order Direction, "left" in descending order.
- If the hierarchy structure of the tree has to be discussed in this article, terms such as “parent” or “ancestor” or “child” or “descendant” are used.
- The hierarchical arrangement of the nodes in the tree structure of the binary search tree is viewed as secondary and more or less random - the correct representation of the sequence is the main focus.
- The question of which node is currently playing the role of the root is similarly secondary, especially if it is a self-balancing tree. In this respect, the address of the root is not suitable for identifying the tree.
- On the other hand, the fixed address of a pointer to the root can be used as the identification of the tree, whose pointer value then has to be maintained by the operations of the tree.
Order relation
In order for binary searching, sorting etc. to work, the order relation must be a total quasi-order , in English "total preorder". The terms for the induced duplicate relation and the induced strict partial order are as there .
The trichotomy of a corresponding 3-way comparison function - only the sign of its result is relevant - results as follows:
| , | if | ( less than ), | ||
| , | if | ( Duplicate of ), | ||
| , | if | ( greater than ). |
After interchanging and and rearranging, you can see that
- .
The induced order relation is a strict weak ordering , in English weak strict ordering . It induces a strict total order on the equivalence classes of this relation, more precisely: the equivalence classes of the duplicate relation .
Obviously, any such order can be mirrored; H. swap with , the result is again a strict weak order. Neighborhood relationships remain, only "bigger" is swapped with "smaller" or "right" with "left".
Remarks:
- A two-way comparison function, which indicates whether two “keys” are the same or not, is basically sufficient for a mere search . With such a comparison function, however, efficient search times, for example logarithmic on average, cannot be achieved.
- For the functioning of the sorting and binary search, it is irrelevant whether the splitting of the unequal path of a 2-way comparison function into a smaller and a greater path is an artifact, such as the arrangement of the letters in an alphabet , or whether a closer / further or logical relationship is involved.
- If the order relation also reflects the neighborhood, this can be used for an efficient "fuzzy search" .
- The node-oriented storage matches the search with the 3-way comparison function exactly.
- As explained in more detail in the “Search” section below, the handling of duplicates is independent of whether the order relation allows duplicates ( total quasi-order or strict weak order ) or not ( total order or strict total order ). On the one hand it can un be desirable, even if it allows duplicates to have this in the tree. On the other hand, it may well be appropriate to include duplicates in the tree even with a total order, for example from the input stream. In practical use, it only depends on whether there should be duplicates in the tree or not. Consequently, total quasi-orders are assumed from the outset.
Search
The search for an entry proceeds in such a way that the search key is first compared with the key of the root . If both are the same, the entry (or a duplicate) has been found.
Otherwise (if “not equal”) a check is made as to whether the search key is smaller (larger) than the key in the node: then the search is continued recursively in the left (right) subtree of the root; if there is no left (right) subtree, the entry you are looking for does not exist in the binary search tree.
The final “not equal” node obtained in this way, together with the last comparison direction, represents the so-called insertion point for the element sought. (In the perspective of Fig. 1B, the external node, which also contains the direction, is sufficient.) It is inserted here , then the in-order matches the sort order. The final “not equal” node has a key that is either the smallest of the larger or the largest of the smaller. The same applies, in reverse, to its neighboring node in the last comparison direction, if there is one. (However, this is not an "insertion point", but an ancestor of the same.)
Search without duplicates (recursive)
The following pseudocode Find illustrates how the algorithm works for a search in which duplicates should never be included in the tree. (This is ultimately independent of whether the order relation allows duplicates or not.)
The function returns a node and a comparison result. Except for the comparison result "Equal", this pair represents an insertion point.
Find(t, s) {
t: binärerSuchbaum
s: Suchschlüssel
return Find0(t, s, t.root, Empty)
// zurück kommt ein Knoten und ein Vergleichsergebnis
}
Find0(t, s, x, d) {
t: Teilbaum
s: Suchschlüssel
x: Knoten
d: Vergleichsergebnis (Equal, LessThan, GreaterThan oder Empty)
if x ≠ null then {
if s = x.key then return (x, Equal) // Suchschlüssel s gefunden
if s < x.key
then return Find0(x, s, x.left, LessThan)
else return Find0(x, s, x.right, GreaterThan)
}
return (t, d) // Suchschlüssel s nicht gefunden
// zurück kommt (Knoten,Vergleichsergebnis) oder (Baum,Empty)
}
In the example chosen in Fig. 2, Find would return the first hit, the upper 'F', as the result for the search key s = 'F'.
Search without duplicates (iterative and with Sentinel)
The following FindWithSentinel function has exactly the same functionality as the Find above . The trick with the guard node or sentinel saves one query per iteration step, namely the query for the absence of the child node, i.e. (= height). It is programmed iteratively here in the C programming language presented.
Note: Since the node is required for the "found" result, but the last parent node is required for the "not found" result, two variables are used alternately in the hot loop.
typedef struct NODE { // Knoten des binären Suchbaums
Node* lChild; // -> linker Kindknoten
Node* rChild; // -> rechter Kindknoten
int key; // Schlüssel
} Node;
typedef struct RESULT { // Ergebnisstruktur mit zwei Feldern
Node* resNod; // -> Ergebnisknoten
int resDir; // Vergleichsergebnis (Equal, LessThan, GreaterThan oder Empty)
} Result;
typedef struct BinarySearchTree { // Der binäre Suchbaum
Node* root; // -> Wurzel des Baums
} Bst;
Bst bst;
Node Sentinel, *sentinel = &Sentinel; // Der Wächterknoten und sein Zeiger
Sentinel.lChild = sentinel; Sentinel.rChild = sentinel;
// Initialisierung des leeren binären Suchbaums:
bst.root = sentinel; // Indikator, dass die Wurzel .root fehlt.
// Dieser Zeiger ist auch von den Einfüge- oder Löschfunktionen
// an den Stellen zu verwenden, wo es einen Kindknoten nicht gibt.
int FindWithSentinel(
Bst* t, // -> binärer Suchbaum
int sKey, // der Suchschlüssel
Result *r) // -> Ergebnisstruktur
{ Node *x, *y;
sentinel->key = sKey; // präpariere den Wächterknoten Sentinel
y = (Node*)t; // »Elter« der Wurzel
// Suchschleife:
for (x = t->root; sKey != x->key; ) {
if (sKey < x->key)
y = x->lChild; // ein echter oder der Wächter-Knoten
else
y = x->rChild; // dito
if (sKey == y->key) { // Schlüsselgleichheit
r->resNod = y; // Ergebnisknoten
goto Epilog;
}
if (sKey < y->key)
x = y->lChild; // dito
else
x = y->rChild; // dito
}
// Abbruch-Bedingung Schlüsselgleichheit: sKey == x->key
r->resNod = x;
x = y; // Elterknoten von r->resNod
Epilog:
if (r->resNod != sentinel) { // Der Ergebnisknoten r->resNod ist echt
// und zeigt auf einen Schlüssel mit Wert sKey.
r->resDir = Equal;
}
else { // Der Ergebnisknoten r->resNod ist unecht.
// x ist der »Elter« von r->resNod
r->resNod = x; // -> Ergebnisknoten (->Node oder ->Bst)
if (x != (Node*)t) { // x ist ein echter Knoten (->Node)
if (sKey < x->key) {
r->resDir = LessThan;
else
r->resDir = GreaterThan;
}
else // x ist der Baum (->Bst)
r->resDir = Empty;
}
return r->resDir;
// *r enthält (->Node,Vergleichsergebnis) oder (->Bst,Empty)
}
Search when duplicates are allowed
If entries of duplicates in the tree are to be permitted, it is advantageous not to abort the search at the first best node found, but to continue searching either on the smaller or on the larger side up to the leaves. This supports the targeted insertion of duplicates and is particularly interesting if the search tree should not only be searched and found, but U. is also traversed . The use of the following search functions in the Binary Tree Sort sorting process makes this process a "stable" one (see Stability (sorting process) with explanatory examples).
With the following pseudocode FindDupGE , the user specifies the direction on the right , on which side of the duplicate a new one should be inserted. In the case of a function FindDupLEwith the mirrored comparison if s ≤ x.key, a new duplicate would be inserted to the left of all existing duplicates.
FindDupGE(t, s, c) {
t: binärerSuchbaum
s: Suchschlüssel // FindDupGE: falls s ein Duplikat ist,
// soll es rechts (GE:≥) eingefügt werden.
c: Cursor { // Dieser Cursor enthält am Ende:
c.d: Richtung // (1) Left, Right oder Empty
c.n: Knoten // (2) Knoten oder Baum (nur bei Empty)
}
c.n = t // Für den leeren Baum
return FindDupGE0(t.root, s, c, Empty)
// zurück kommt ein Einfügepunkt im Cursor c
}
FindDupGE0(x, s, c, d) {
x: Knoten
s: Suchschlüssel
c: Cursor
d: Richtung
if x ≠ null then {
c.n = x
if s ≥ x.key // Suchschlüssel s ≥ Knoten.Schlüssel?
then return FindDupGE0(x.right, s, c, Right) // ≥ (GE)
else return FindDupGE0(x.left, s, c, Left) // <
}
c.d = d // Setzen Einfüge-Richtung
return c
// zurück kommt ein Einfügepunkt im Cursor c
}
The pair ( Knoten, Richtung) of the previous example Findis combined here to form the one object called Cursor. It is a pure output parameter that specifies the insertion point.
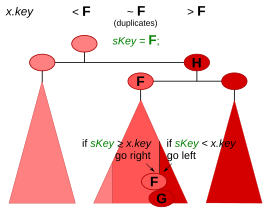
FindDupGEis kept in such a way that an immediate insertion point is always returned in the result cursor . From the result, however, it is not immediately clear whether it is a duplicate, since the insertion point does not have to have the key you are looking for, even if it occurs in the tree. This depends on the more or less random arrangement of the nodes in the tree. If the rightmost duplicate (in the example in Fig. 2 the lower right 'F') is not a half leaf to the right, then in the hierarchy of the binary tree it is an ancestor of its right neighbor (in the example 'G'), who is now a half leaf after is left and together with the direction "left" specifies the same insertion point and thus in this case represents the result of .
FindDupGE
While Findall 3 ways of the comparison function are queried, it is sufficient to FindDupGEquery their 2.
The following pseudocode FindDup combines the capabilities of Findand FindDupGEby providing both a result on the existence of a search key and an insertion point for duplicates. To do this, the user specifies a direction d(left or right) on which side of the duplicate a new one should be inserted. The result is a pair ( Knoten, Cursor), Knotenindicating whether and where the search key was found.
The proposal builds an example of an object that is called a cursor (in analogy to the databases, for example ) . The #Cursor contains the entire path from the result node to the root. It thus fits the subsequent in-order traversal function , a version that does not require a pointer to the parent node. The appropriate data structure for the path is the stack memory . Stack , with the operations and .
Nextpushpop
The somewhat simpler version of the function, which assumes a pointer to the parent in each node and therefore the cursor does not need a stack, does not have to call the pushand clear. However, the memory requirement for the tree increases by one pointer per node.
FindDup(t, s, c, d) {
t: binärerSuchbaum
s: Suchschlüssel
c: Cursor { // Dieser Cursor enthält am Ende:
c.d: Richtung // (1) Left, Right oder Empty
c.n: Knoten // (2) Knoten oder Baum (nur bei Empty)
// Die folgenden 2 nur, wenn die Elterknoten fehlen:
c.t: Baum // (3) Baum (enthält den Zeiger zur Wurzel)
c.p: Pfad // (4) Pfad vom Elter des Knotens zur Wurzel
}
d: Richtung // Falls s ein Duplikat ist, soll es ...
c.d = d // … auf dieser Seite eingefügt werden.
c.t = t // initialisiere den Cursor
clear(c.p) // initialisiere den Stack
c.n = t // für den leeren Baum
return FindDup0(t.root, s, c, Empty)
// zurück kommt ein Knoten und ein Einfügepunkt im Cursor c
}
FindDup0(x, s, c, d) {
x: Knoten
s: Suchschlüssel
c: Cursor
d: Richtung
if x ≠ null then {
push(c.p, c.n) // Elter c.n von x in den Stack
c.n = x // setze neuen Knoten im Cursor
if s = x.key then return FindDup1(x, s, c, c.d)
if s < x.key
then return FindDup0(x.left, s, c, Left)
else return FindDup0(x.right, s, c, Right)
}
c.d = d // Setzen Einfüge-Richtung
return (null, c) // Suchschlüssel s nicht gefunden
// zurück kommt null und ein Einfügepunkt im Cursor c
}
FindDup1(q, s, c, d) {
q: Knoten // letzter Knoten mit Equal
s: Suchschlüssel
c: Cursor
d: Richtung
x: Knoten
x = c.n.child[d]
if x ≠ null then {
push(c.p, c.n) // Elter c.n von x in den Stack
c.n = x // setze neuen Knoten im Cursor
if s = x.key
then return FindDup1(x, s, c, c.d) // x ist neuer Knoten mit Equal
else return FindDup1(q, s, c, 1 - c.d) // bei ≠ weiter in der Gegen-Richtung
}
c.d = d // Setzen Einfüge-Richtung
return (q, c)
// zurück kommt ein Duplikat und ein Einfügepunkt im Cursor c
}
FindDupis kept in such a way that an immediate insertion point is always returned in the result cursor . If the search key was not found, the null pointer is returned in the Node field . If the search key has been found, the leftmost or rightmost duplicate, in the example in Fig. 2 the rightmost duplicate 'F', returns as the found node. The insertion point can coincide with the node found; however, it can also be its immediate neighbor (right in the example in the figure), in which case it has a different key (in the example 'G').
FindDup
In the first part FindDup0,, all 3 ways of the comparison function are queried; in the second part, FindDup1if the existence of the search key has been positively clarified, only the second one.
complexity
Since the search operation runs along a path from the root to a leaf, the time spent depends on the average and in the worst case linearly on the height of the search tree ( complexity ); in the asymptotically negligible best case the running time is constant at , but always at andFindFindDupGEFindDup
In the degenerate case, the height is as great as the number of elements present . When building a tree, which corresponds to a sorting run, in extreme cases each element must be compared with each one - results in comparisons in total .
Weight-balanced search trees can have a constant runtime on average, but behave linearly in the worst case. Height- balanced search trees have a height of and thus enable searches in guaranteed logarithmic runtime . The structure of a tree then comes down to comparisons - this corresponds to the best sorting algorithms.
Logarithmic height even applies on average to randomly generated search trees if the following conditions are met:
- All permutations of the elements to be inserted and deleted are equally likely.
- If the tree is modified, there is no "asymmetrical" delete operation, i. H. the descents in the deletions to the left and those to the right are balanced on average.
Search depths and path length sums
Let be a set of keys from a totally ordered reservoir of keys, let further be or frequencies with which the element is accessed, where for resp. for . (Let and additional non- belonging elements with the usual meaning.) The - tuple
means access distribution for the crowd when everyone is. becomes the access probability distribution if is.
Let us now be a search tree for the set with an access distribution , and let the depth of the (inner) node and the depth of the (external) leaf (see Fig. 3; each #terminology of Fig. 1B). We consider the search for an element . If so , we compare it to elements in the tree. If so , we compare it to elements in the tree. So is
the weighted path length sum of the tree (with the access distribution ) ; is a probability distribution, then is the weighted path length , the weighted search depth, or the mean number of comparisons required. Fig. 3 shows a search tree which , with a value of, is optimal for the access distribution .
If all and all , then using is the sum of the comparisons required when searching for each of the nodes ( for a successful search). It is the so-called internal path length in a Relationship
- .
For all binary search trees is:
- ,
where the upper bound comes from the linear chain and the lower from the fully balanced binary trees . The function is piecewise linear , strictly monotonically increasing and convex downwards ; in formulas: is with , then is .
By the way, the sequence A001855 is in OEIS .
If, on the other hand, all and all , then with is the sum of the necessary comparisons to find all sheets ( for missing ). is also known as the external path length :
- .
It applies to all trees :
- .
- proof
The claim is correct for .
Be a tree with knots. If there is a node at the level , we add a new edge and a new node. increases by and by , so the difference increases by . ■
The fully balanced binary trees are also optimal for access distribution , and the following applies to all binary search trees :
with .
Incidentally, the sequence A003314 is in OEIS , and is the number of external nodes (leaves).
Traversal
Traversing (crossing) refers to the systematic exploration of the nodes of the tree in a certain order.
There are several ways to iterate through the nodes of binary trees . In the binary search tree, however, the so-called in-order or reverse in-order traversals are clearly preferred, as they reflect the imprinted order relation.
In the literature there are almost exclusively (recursive) implementations that only run over the entire tree - examples in binary tree # Recursive implementations . The actions to be carried out at the individual nodes are then to be programmed in a so-called callback function (there:) callback.
A single traversal, as suggested in the following section, can be used much more flexibly in practice.
Traversal (single step)
The following pseudocode Next, starting from a node, returns the next element in descending or ascending order - an iterative implementation. The proposal does not require a pointer to the parent node. For this, the input object , here called #Cursor , must contain the entire path from the current node to the root, and this must also be maintained accordingly by the Nextfunction if it is used Nextin a loop. The appropriate data structure for the path is the stack memory . Stack , with the operations pushand pop.
The somewhat simpler version of the function, in which a pointer to the parent is assumed in each node and therefore the cursor does not need a stack, is listed in the binary tree . However, the memory requirement for the tree increases by a fixed percentage.
During a longer traversal (multiple calls to Next), half leaves and higher-ranking ancestors alternate.
Next(c) {
c: Cursor { // Dieser Cursor enthält:
c.d: Richtung // (1) EndOfTree oder Left, Right
c.n: Knoten // (2) Baum (nur bei EndOfTree) oder Knoten
c.t: Baum // (3) Baum (enthält den Zeiger zur Wurzel)
c.p: Pfad // (4) Pfad vom Elter des Knotens zur Wurzel
}
x,y: Knoten
x = c.n // Ausgangsknoten dieses Einzelschritts
d = c.d // gewünschte Richtung der Traversierung
y = x.child[d]
if y ≠ null then { // 1 Schritt in die gegebene Richtung
push(c.p, x) // Elter x von y in den Stack
d = 1 - d // spiegele Left <-> Right
// Abstieg in Richtung Blätter über Kinder in der gespiegelten Richtung
x = y.child[d]
while x ≠ null do {
push(c.p, y) // Elter y von x in den Stack
y = x
x = y.child[d]
}
c.n = y // Ergebnis: das nächste Halbblatt in Richtung c.d
return c // (Es ist Halbblatt auf seiner (1-c.d)-Seite.)
}
// Am Anschlag, deshalb Aufstieg zur Wurzel über die Vorfahren in der ...
do { // … c.d-„Linie“ (nur linke oder nur rechte)
y = x
x = pop(c.p) // Elter von y aus dem Stack
if x = c.t then { // y ist die Wurzel.
// Somit gibt es kein Element mehr in dieser Richtung.
c.n = c.t // Ergebnis: der Baum als Elter der Wurzel
c.d = EndOfTree // signalisiere das Ende der Traversierung
return c
}
} until y ≠ x.child[d]
// Es gab beim Aufsteigen einen Richtungswechsel:
c.n = x // Ergebnis: der erste Vorfahr in der gespiegelten Richtung
return c
}
The traversal over the whole tree includes one descent and one ascent per edge ; so the effort at knots is . Therefore the effort for a single traversal is constant on average and amortized and in the worst case in O (h) with h as the height of the tree.
It makes no difference whether the query for the presence of the child node occurs as (x ≠ null)or with a guard node (see section #Search without duplicates (iterative and with Sentinel) ) - neither functionally nor in terms of runtime. Since the traversal always compares with the address of x a node, no advantage is to be expected from the preparation of a guard node with a value .
Proximity Search
Each search function can be combined with the single-step traversal shown above to form an “ approximate match ” search . This is a search in the vicinity of a certain key, for example on "greater than or equal to" (or "less than or equal to").
The above search functions Find, FindDupGEand FindDupprovide an insertion point in the “not equal” case . If the tree is not empty, this contains an element that is either the smallest among the larger ones or the largest among the smaller ones. In the first case, the “greater than or equal” wish can be satisfied directly. In the latter case, you go to the next element in ascending order, if there is still one, and return it because it has to be a larger one. The logic for the mirrored version is obvious.
The Index Sequential Access Method has similar functionality .
An important application is the mapping of several linearly sorted keys to a single linear order with the help of a space-filling curve , e.g. the Hilbert index . Here, the poorer accuracy of the key formed in this way may have to be compensated for by good neighborhood properties.
Insert
It is assumed that the navigation to the insertion point is already done. Insertion point means a node and a direction (right or left). An immediate insertion point in a binary tree is always a right (or left) half leaf (i.e. a node without a right (or left) child node ) together with this direction. (In the perspective of Fig. 1B, this corresponds exactly to an external node, whose addresses must then all be different and which, for example, may not be implemented as a Sentinel .) An indirect one is the immediate neighbor in the specified direction and specifies together with the opposite direction is the same place in the binary tree - for real insertion, however, the insert function must descend to the half-sheet that represents the immediate insertion point. The above functions Find, FindDupGEand FindDupdeliver an (immediate) insertion point as a result ( Findnot for "Equal").
To insert, let the immediate insertion point (the child in the appropriate direction) point to the new element, so that it is inserted correctly according to the total quasi-order. The complexity of the insert operation (without searching) is therefore constant. If a search operation is added (as is very often the case in the literature), this dominates the complexity.
Once inserted, the new element is a leaf in the search tree.
Repeated insertion of keys sorted in ascending (or descending) order can lead to the tree degenerating into a linear list.
Clear
As explained in the Deletion section of the Binary Tree article, there are various ways of removing a node from a binary tree while maintaining the previous in-order order. Since this coincides with the search order for the search trees, the following procedure proposed by T. Hibbard in 1962 is recommended, which ensures particularly small changes to the heights of the subtrees.
The node to be deleted is denoted by.
- Has two children, go to step 4. Otherwise, it is a leaf or has only one child. This is indicated with .
- Was the root, then becomes the new root. Finished!
- Otherwise set parent and make on s site and child toward the child . Is a knot, becomes the new parent of . Finished!
- Has two children, navigate in the right child tree from to the leftmost node . He is the in-order successor of and cannot have a left child.
- Set parent and child direction , which is left, if , otherwise right.
- Copy keys and data from into the node .
- Set right child . It can be missing. Make (in place of) a child . If there is a knot, it becomes the new parent of .
- Conclusion
- In a binary search tree, where only the (in-order) order is important in the tree, you can swap the target node with one (of a maximum of two) in-order neighboring nodes when deleting and what the tree structure with its pointers etc. concerns removing this instead of that from the tree. One of the two, the target node or the neighboring node, has at most one child.
The height of -child decreases by from to when the height is from .
Repeated deletion can lead to the tree degenerating into a linear list.
Because of the inevitable descents to the half-leaves, the complexity of the delete operation is at its worst , where the height of the tree is.
If duplicates are allowed in the tree, Mehlhorn suggests clearing elements with the same key in the Last In - First Out discipline.
implementation
The figure shows an obvious type of storage. It roughly corresponds to the C structures:
struct node { // 1 Objekt = 1 Knoten
char key;
struct node * Kind_links;
struct node * Kind_rechts;
} object;
struct node * Kopf; // Zeiger auf die Wurzel
To distinguish between the objects are these beziehentlich with the keys , , and provided. These keys are also used as reference targets for simplicity (instead of real memory addresses ). As usual, a pointer value 0 should express that no object is referenced, i.e. that there is no child at this point.
head
Since the root is subject to a deletion or a rotation and thus can not represent the tree , this role has to be taken over by another data structure, which is called head in the literature . It contains the pointer to the root and acts as a kind of parent of the root.
Iterative programming
In the literature, the operations are often presented in recursive programming . However, the user has several advantages if the implementer has replaced the recursions, which are elegant in terms of writing, with simple iterations, since this saves (height) procedure calls and returns and the memory requirement for the program stack is kept constant. But it's not just about conserving resources. In the traversal operation, for example, this simplifies the programming of the application . To keep the way back to the root and head, which is needed when traversing, but also often when making modifications to maintain the tree variants (AVL or red-black criterion) and which is in the program stack among other things during recursive programming, then another, explicit construct can be selected, which can be subsumed in the cursor (see below) .
This enables the modifying operations to be separated from the navigation.
It makes sense to separate insert and delete operations from the search operation if you want to navigate to the insertion point or node in a way other than the standard search operation, for example using a cross step or using a second search structure for the same element as in the # application with multiple access paths .
This modularization of the navigation operations from the modifying operations releases a possibly sub-logarithmic (read: constant) effort of the latter, because an ascent to the root is only necessary in exceptional cases , for example with the AVL tree and the red-black tree . In applications with a strong sequential component, this can have a positive effect on the runtime.
cursor
When searching, a pair ( node , direction ) is created which is suitable for specifying the insertion point when inserting . When deleting, the node to be deleted is designated by the node component , and the direction component can indicate where the cursor should proceed after the deletion. When traversing, the node indicates the starting point and the direction the desired direction of the navigation in order to arrive at such a pair again as a result. In this way, all important operations generate and / or consume a construct which is called a cursor (by analogy with databases, for example ) .
The size of the cursor depends largely on whether the nodes contain a pointer to the parent or not.
-
Parent pointer present: A pair ( node , direction ) represents a full-fledged cursor.
A cursor becomes invalid after an operation if and only if it involves a deletion and the node of the cursor is the target of the deletion.
With the percentage surcharge on the storage requirement for the data structure, you definitely buy a percentage saving in runtime, since the way back to the root and head is always secured. - Pointer to parent node not available ("cursor with stack"): In addition to the pair ( node , direction ), the path from the node to the root and head must be kept in the cursor. The length of the cursor thus corresponds to the maximum height of the tree. This is either sufficiently limited on its own (precalculated example AVL tree ), or the stack overflow triggers a reorganization of the tree or an abnormal end.
For all operations, access to the parent node via the stack in the cursor is slightly more expensive than via the parent pointer. If the path in the cursor is to be kept valid even after a modifying operation (e.g. for sequential insertions or deletions), there is an additional percentage surcharge. However, this can only be done for one cursor, the input cursor.
If an application requires multiple cursors for the same search tree and across changes to it, maintaining the consistency of the cursors with stacks (e.g. by searching again) can become so laborious that it is more economical to give the tree parent pointers.
Application with multiple access paths
A classic memory management is given as an example of an application with 2 access paths. Elements of the data structure are the free memory blocks with the attributes (fields) location and size . There is a search structure for each of the two fields, with location without duplicates. However, since duplicates are unavoidable for size , a lexicographically composed key ( size , location ) is recommended . When acquiring , a block of minimum size is searched for, removed and the remainder, if any, entered again. When the memory is returned, the location is searched for, there is a check to ensure that there are no conflicts with the neighboring blocks (also an example of the usefulness of the cross steps ) and the block to be returned is merged with these if necessary. All changes must be carried out on both search structures. If parent pointers are available, shuffling from one search structure to the other saves a search process.
Applications
As Ben Pfaff shows, the dynamic search tree structures AVL tree , red-black tree and splay tree cover the same essential functions. He found major differences in the runtime behavior, with the AVL tree performing best in median and mean.
In computer science, the dynamic search tree structures have a large area of application as basic tools for:
- Duplicate suppression, deduplication , duplicate detection
- Elementary set operations such as averaging and union
- Standard Template Library (STL)
At Ben Pfaff there are system-related applications (all under × 86-based Linux):
- Management of virtual memory areas (VMAs) including range queries to determine the overlap of existing VMAs (p. 4)
- Unique identification of IP packets (p. 7)
Further:
- List of the variables in a program that an interpreter has to maintain: the interpreter must be able to decide at any time whether a value is currently assigned to a program variable and, if so, which one. The same applies to a compiler .
- Binary Tree Sort (sort by insert)
- Classic storage management in # application with multiple access paths .
Selection criteria
The binary search in the array can be seen as a kind of forerunner of the binary search trees. Since it behaves linearly with insertions and deletions and the memory management of its array has to be carefully considered, in practice it is almost only used for static, pre-sorted tables. So if insertions or deletions are important for the application, the binary trees are more suitable. With regard to search time and memory, binary searches in the array and height-balanced binary search trees behave asymptotically the same.
Although purely random binary search trees behave logarithmically on average, a binary search tree without any precautionary measures to counteract degeneracy does not guarantee a sub-linear running time. Degeneracy can occur systematically, for example when a programmer assigns a large number of closely adjacent jump label names.
However, there are a great many concepts that have been developed to ensure a sufficient balance. Here there are always expenses and income in opposition. For example, the effort to keep a binary search tree completely balanced at all times is so high that it should only be worthwhile for applications whose runtime is extremely dominated by the search.
An important criterion for the selection is whether the binary tree is static, and thus a one-time optimal structure is sufficient, or whether changing operations such as insert and delete are important. For the former, weighted search trees can be considered, including the Bellman algorithm . For the latter, height-balanced search trees such as the AVL tree and the red-black tree , but also splay trees, are of interest.
A comparison of the complexities of different search algorithms can be found in the article Search tree ; Runtime measurements based on realistic examples can be found at Pfaff 2004b .
In these considerations, it was generally assumed that the entire tree is accommodated in the working memory (main memory). If access to external media plays a role, completely different criteria apply. Even the B-tree , which takes into account such aspects, is a search tree, but no longer binary.
Historical
The well-known search structure binary search in the array mentioned in the section Motivation is considered to be the forerunner of the dynamic search tree structures. As an obvious implementation of looking up in a (sorted) dictionary, it should have been developed and implemented several times and without knowledge of other implementations. In the dynamic application, however, it cannot keep up with the more recent developments, although in the static case it is an excellent solution. There are macros which cause a compiler to generate source code for an iterating or loopless binary search for a given (sorted) table of (key, value) pairs .
In 1962, a dynamic search tree structure in the form of the AVL tree appeared for the first time . Its inventors are the aforementioned Soviet mathematicians Georgi Adelson-Welski and Evgeni Landis. Her contribution to the journal Doklady Akademii Nauk SSSR was translated into English that same year. The translation (like the original) bears the very ambitious title “An algorithm for the organization of information”. The designation AVL tree does not appear in this translation.
In 1970 Rudolf Bayer published his first work on the B-tree . It is not a binary tree, supports heterogeneous storage, e.g. main storage and background storage, and is used in database systems.
This was followed in 1972 by Rudolf Bayer's red-black tree under the name “symmetric binary B-tree” . The balance rule of the AVL tree was too strict for him. A renaming took place in 1978 by Leonidas Guibas and Robert Sedgewick in the now common "red-black tree", later also "RB tree".
Splay trees were introduced in 1985 by Daniel Sleator and Robert Tarjan under the name "Self-Adjusting Binary Search Trees". They are even more dynamic than the above in that they also change during search operations.
A rough comparison of dynamic search trees can be found in
See also
literature
- Donald E. Knuth : The Art of Computer Programming . Volume 3: Sorting and Searching . 3. Edition. Addison-Wesley, 1997, ISBN 0-201-89683-4 .
- Kurt Mehlhorn : data structures and efficient algorithms. Teubner, Stuttgart 1988, ISBN 3-519-12255-3 .
- Kurt Mehlhorn , Peter Sanders : Algorithms and Data Structures. The Basic Toolbox . Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-77977-3 , doi : 10.1007 / 978-3-540-77978-0 .
Web links
- Ben Pfaff: An Introduction to Binary Search Trees and Balanced Trees . (PDF, gzip; 1675 kB) 2004 (English).
- Ben Pfaff: Performance Analysis of BSTs in System Software . (PDF; 316 kB) Stanford University , 2004 (English).
References and comments
- ↑ If there are no values, but only keys, the underlying model is that of the finite set , and the question is reduced to whether a given key is present in the set or not. So the indicator function of the quantity has to be realized.
- ↑ The perspective of Fig. 1B can be found, for example, in #Knuth and in the article Rot-Schwarz-Baum . An explicit comparison of the two perspectives is provided by #Pfaff 2004a , p. 30 "4.1.1 Aside: Differing Definitions". There, the perspective of Fig. 1A is referred to as that of the implementer.
- ↑ # Mehlhorn 1988 p. 296
- ↑ whose compliance with the relations laws the software cannot verify
- ↑ #Pfaff a § 23
- ↑ #Mehlhorn 2008
-
↑ as
locateLocallyin #Mehlhorn 2008 p. 150 - ↑ after # Mehlhorn 1988 p. 147
- ↑ internal path length at #Knuth pp. 399-400
- ↑ external path length at #Knuth pp. 399-400
- ↑ at #Knuth .
- ↑ a b quoted from: Robert Sedgewick , Kevin Wayne: Algorithms Fourth Edition. (PDF) ( Page no longer available , search in web archives ) Info: The link was automatically marked as defective. Please check the link according to the instructions and then remove this notice. Pearson Education, 2011, ISBN 978-0-321-57351-3 , p. 410 (English), accessed March 25, 2018
- ↑ You can just as easily navigate in the left child tree from to the rightmost node, which is the in-order predecessor of and cannot have a right child.
- ↑ The chosen way of speaking serves only to make it easier to understand. Of course, a generic software package must remain independent of user data and proceed vice versa, namely leave the user data of the node that is not necessarily known to it untouched and equip it with all the connections of the node belonging to the binary search tree , as well as allow all pointing pointers to point. This includes that if the root was, the node becomes the new root.
-
^ So in Exercise 7.10. in #Mehlhorn 2008 p. 155. The above functions
FindDupGEandFindDupLEsupport this if the same is used for inserting and deleting. If the other function is used, e.g. when insertingFindDupGEand deletingFindDupLE, then a first in - first out discipline is implemented. - ^ "Header node" and "HEAD" in Donald E. Knuth: The Art of Computer Programming , Volume 3, Sorting and Searching, 2nd edition, Addison-Wesley, 1998, p. 462; totum pro parte "tree data structure" from Ben Pfaff: An Introduction to Binary Search Trees and Balanced Trees. Free Software Foundation, Inc. Boston 2004.
- ↑ See also Traversierung (with code examples) and Ben Pfaff: An Introduction to Binary Search Trees and Balanced Trees. Free Software Foundation, Inc. Boston 2004, p. 47 "4.9.2 Traversal by Iteration".
- ↑ Ben Pfaff gives an object with very similar functionality the name "traverser" and offers a standard and a traverser variant for searching, inserting and deleting. ( #Pfaff 2004a , p. 15 "2.10 Traversers")
- ↑ "auxiliary stack" at #Knuth (p. 461), which solves the insertion in the AVL tree in another way.
- ↑ a b Ben Pfaff: Performance Analysis of BSTs in System Software. Stanford University 2004.
- ^ Rudolf Bayer , Edward M. McCreight: Organization and Maintenance of Large Ordered Indices . Mathematical and Information Sciences Report No. 20. Boeing Scientific Research Laboratories, 1970.
- ^ Rudolf Bayer: Symmetric binary B-Trees: Data structure and maintenance algorithms . In: Acta Informatica . 1, No. 4, 1972, pp. 290-306. doi : 10.1007 / BF00289509 .
- ↑ Leonidas J. Guibas, Robert Sedgewick : A Dichromatic Framework for Balanced Trees . In: Proceedings of the 19th Annual Symposium on Foundations of Computer Science ., Pp. 8-21. doi : 10.1109 / SFCS.1978.3
- ^ Daniel D. Sleator, Robert Tarjan : Self-Adjusting Binary Search Trees . In: Journal of the ACM ( Association for Computing Machinery ) . tape 32 , no. 3 , 1985, pp. 652–686 , doi : 10.1145 / 3828.3835 ( cs.cmu.edu [PDF; 6.1 MB ]).