Binary search
The binary search is an algorithm that finds a searched element very efficiently in a field (ie mostly “in a list”) or provides reliable information about the absence of this element. The prerequisite is that the elements in the field are arranged (“sorted”) according to a total order relation . The algorithm is based on a simple form of the divide- and- conquer scheme , at the same time it is also a greedy algorithm . Order and later search must refer to the same key .
algorithm
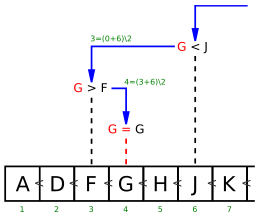
First the middle element of the field is checked. It can be smaller, larger or equal to the element you are looking for. If it is smaller than the element you are looking for, the element you are looking for must be in the back half, if it is there at all. If, on the other hand, it is larger, you only have to search in the front half. The other half no longer needs to be considered. If it is the same as the element searched for, the search is over.
The same procedure is followed in the half to be examined (and again in the following halves): The middle element again provides the decision as to whether and where to continue searching. The length of the search area is halved from step to step. The search is ended at the latest when the search area has shrunk to a single element. This one element is either the element searched for or the element searched for does not occur.
The binary search algorithm is implemented as either iteration or recursion . In order to be able to use it, the data must already be sorted and present in a data structure in which the nth element can be accessed “directly”. Efficiency would be lost on a simple linked list (but see skip list ).
complexity
A maximum of comparison steps are required to determine the presence or absence of a key in a field with entries . Thus, when expressed in Landau notation , binary search has the time complexity . This makes it significantly faster than the linear search , which however has the advantage that it also works in unsorted fields. In special cases the interpolation search can be faster than the binary search.
Similar procedures and variants
Interval nesting
The binary search method described here can be viewed as a (finite) version of the interval nesting from mathematical analysis.
Binary search tree
The search algorithm also corresponds to the search in a binary search tree if the array is interpreted as such: the middle element is the root, the middle of the halves that are created are the roots of the corresponding subtrees and so on. The binary tree resulting from this interpretation is even a so-called fully balanced binary tree , i.e. a binary tree in which the lengths of the paths from the leaves to the root differ by at most 1. This also applies regardless of the direction of rounding when calculating the mean value of the indices. The resulting binary tree is (like the binary search) optimal among all binary trees with elements with respect to
- the maximum path length (= height of the tree),
- the path length sum that results in, and
- the mean path length.
The latter corresponds to the mean number of comparisons if all elements are equally likely.
If you don't split in the middle, the result is still a binary search tree, but it may be. U. not balanced and not optimal.
The great superiority of the binary search tree compared to the binary search in the array is firstly in the better behavior in the case of insertions and deletions, which on average incur a linear effort. In the case of trees, there are also implementations with a guaranteed logarithmic runtime in these cases. Memory management is also easier there, since changes do not affect the entire array, but can be directly linked to the emergence or disappearance of an element. Second, trees can be adjusted for frequencies better than the array . But if the array is already sorted and then no longer changes and access probabilities are irrelevant, the array is a good method.
Binary search and total quasi-order
Since the array can be viewed as the finite domain of a function, which of course does not necessarily have to be injective , the occurrence of duplicates can easily be controlled via the function values. And if the order relation is not a total order from the outset , but only a total quasi-order , it may be more economical to create the equivalence classes before the comparison than to keep all possible duplicates in the array.
example
A collection of keywords should be case-sensitive, but the keywords should not differ in their meaning.
Interpolation search
During the interpolation search, the array is not divided in the middle, but the position of the element searched for is estimated using linear interpolation. If the keys are distributed approximately equidistantly, the element you are looking for can be found in almost constant time. In an unfavorable case, however, the term will be linear. Apart from that, the domain must be suitable for linear interpolation.
Square binary search
In the quadratic binary search, one tries to combine the advantages of the interpolation search with those of the normal binary search and to reduce the search space to an interval of length by means of interpolation in each iteration .
Different implementations
This algorithm is available in the class libraries of numerous programming languages. In Java, for example java.util.Arrays.binarySearch, there is the package in Python bisect, in C ++ / STL there is std::binary_searchin the "algorithms" library.
The field position at which the entry was found is returned as the return value. If the entry could not be found, the position is usually returned where it should be. B. negative - as an indication of "was not found". However, subsequent implementations only return "0" or "-1" in this case ("was not found").
In the case of large fields, the calculation of the center position
Variable: Mitte = (Links + Rechts) DIV 2
lead to an overflow when added, which is why often instead
Variable: Mitte = Links + ((Rechts - Links) DIV 2)
is implemented. It should also be noted that the value for the center position can reach 0 and thus the next value for the right edge becomes negative. If you were to use an unsigned data type here, an underflow would take place and the condition of the loop would remain fulfilled.
C.
Example in C (iterative):
/**
* Binäre Suche auf dem Array M nach dem Eintrag suchwert
*
* @param M : zu durchsuchendes Feld
* @param eintraege : Anzahl der Feldelemente
* @param suchwert : gesuchter Eintrag
* @return >= 0: Index des gesuchten Eintrags
* < 0: nichts gefunden
*/
int binary_search(const int M[], const int eintraege, const int suchwert)
{
const int NICHT_GEFUNDEN = -1 ;
int links = 0; /* man beginne beim kleinsten Index */
int rechts = eintraege - 1; /* Arrays-Index beginnt bei 0 */
/* Solange die zu durchsuchende Menge nicht leer ist */
while (links <= rechts)
{
int mitte = links + ((rechts - links) / 2); /* Bereich halbieren */
if (M[mitte] == suchwert) /* Element suchwert gefunden? */
return mitte;
else
if (M[mitte] > suchwert)
rechts = mitte - 1; /* im linken Abschnitt weitersuchen */
else /* (M[mitte] < suchwert) */
links = mitte + 1; /* im rechten Abschnitt weitersuchen */
/* end if */
/* end if */
}
return NICHT_GEFUNDEN;
// alternativ: return -links; // (-Returnwert) zeigt auf kleinstes Element >= suchwert: Platz für Einfügen
}
python
Recursive procedure in Python :
def binaersuche_rekursiv(werte, gesucht, start, ende):
if ende < start:
return 'nicht gefunden'
# alternativ: return -start # bei (-Returnwert) waere die richtige Einfuege-Position
# end if
mitte = (start + ende) // 2
if werte[mitte] == gesucht:
return mitte
elif werte[mitte] < gesucht:
return binaersuche_rekursiv(werte, gesucht, mitte + 1, ende)
else:
return binaersuche_rekursiv(werte, gesucht, start, mitte - 1)
# end if
# end function
def binaersuche(werte, gesucht):
return binaersuche_rekursiv(werte, gesucht, 0, len(werte) - 1)
# end function
Haskell
Example in the functional programming language Haskell (recursive)
data SearchResult = NotFound Integer | Found Integer deriving (Eq, Ord, Show)
bsearch :: Ord a => a -- hiernach wird gesucht
-> (Integer -> a) -- zu durchsuchende Folge, monoton
-> Integer -- Indexuntergrenze (einschließlich)
-> Integer -- Indexobergrenze (ausschließlich)
-> SearchResult
bsearch dest s lo hi
| s lo > dest = NotFound lo
| hi <= lo = NotFound lo
| otherwise = go lo hi
where
-- Invarianten: lo < hi, lo ist immer klein genug, hi ist immer zu groß.
-- Wir suchen den *größten* Index, der klein genug ist.
go lo hi
| lo + 1 == hi = if s lo == dest then Found lo else NotFound hi
| dest < s mid = go lo mid
| otherwise = go mid hi
where mid = (lo+hi)`div`2
Remarks
- ↑ If the field is filled with entries (this corresponds to a complete binary tree of the height ), all halves have a remainder of 0.