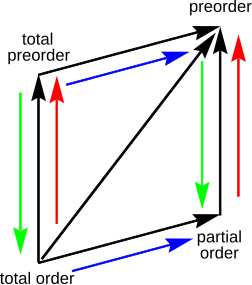
Quasi order
A quasi-order , also pre-order , (English preorder ) is a weakened variant of a partial order , in which it is possible that different elements are comparable in both directions. The antisymmetry does not have to be fulfilled.
Any two-digit relation can be expanded to a quasi-order by forming its reflexive-transitive envelope .
In particular, the total quasi-orders occur in practical applications when arranging objects in sorting processes , spreadsheet programs or databases .
Definitions
Quasi order
A two-digit relation on a set is called a quasi-order (English preorder ) if it is reflexive and transitive . So must apply to everyone
(Reflexivity) (Transitivity)
One then calls a quasi-ordered set or, for short, a quasi-order.
Total quasi-order
A quasi-order is called total , also preference order , (English total preorder ), if two elements are always comparable. The following must therefore apply to all :
(Totality)
One then calls a totally quasi-ordered set or, in short, a total quasi-order.
Partial quasi-order
Reflexivity is no longer required for all elements, but only for those that occur somewhere in the relation.
A two-digit relation on a set is called partial quasi-order (English partial preorder ) if it is reflexive and transitive where it is defined. So must apply to everyone
(partial reflexivity) (Transitivity)
One then calls a partially quasi-ordered set or, for short, a partial quasi-order.
properties
- A partial order (English partial order ) is a quasi-ordering.
- A total ordering (English total order ) is a total quasi-ordering (and also a partial order).
- Every equivalence relation is a quasi-order.
- If there is a quasi-order, then applies to everyone . This property is even characteristic of quasi-orders: every relation with this property is a quasi-order.
- If there is a quasi-order, then exactly then applies if applies to all .
- When comparing two quasi-ordered elements and there are a maximum of four options:
is (really) smaller than . is equivalent to (for the antisymmetric quasi-orders : equal) . is (really) greater than . and are not comparable.
- The fourth result does not occur in the total quasi-orders - there are a maximum of three options, and one speaks of a trichotomy of the order .
- With a partial quasi-order, the mutual inclusion is a partial equivalence relation , i.e. symmetrical and transitive.
Examples and counterexamples
- If you compare complex numbers based on their amount , you get a total quasi-order. So the definition is: . This is not a partial order, since, for example, the numbers and are mutually comparable, so and applies.
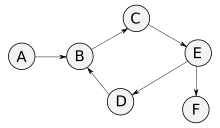
- On the set of nodes of a directed graph , a quasi-order is obtained by specifying that there is a directed path from to ( can therefore be reached from). This quasi-order is a partial order if the graph is cycle-free ( acyclic ), i.e. contains no or only trivial cycles . In fact, every finite quasi-order can be obtained from a suitable graph in this way.
- The divisibility relation | is a quasi-order on the set of integers . It is not a partial order because, for example, 3 | −3, but also −3 | 3 applies. If one considers the divisibility on the set of natural numbers , the antisymmetry is added, so that there is a partial order.
- If the comparison of ( real or rational ) numbers is subject to a fluctuation range ( measurement deviation , inaccuracy), then it is not a quasi-order, since the associated duplicate relation is not an equivalence relation .
- In contrast, comparing after cutting off decimal or binary digits, or more generally after rounding , is a total quasi-order.
- The norms for alphabetical sorting in German are examples of total quasi-orders, which are not total orders, in the case of upper and lower case letters and the treatment of umlauts.
- The IEEE floating point numbers common on computers are
<=a partial quasi-order with the order . It is not fully reflexive because every comparison is wrong for NaN values. Hence there is==only a partial equivalence relation. It is also not a partial order , because+0.0 == −0.0, therefore,+0.0 <= −0.0and+0.0 >= −0.0applies, but the two are not identical: The calculation1.0/(+0.0)gives positive infinity and1.0/(−0.0)negative infinity ; which of course are different.
Induced equivalence relation and strict order
A quasi-ordering on a set produces an equivalence relation - the "canonical" that is to be associated, excellent equivalence relation - on by setting
- .
So two elements are equivalent if they are mutually comparable. For the sake of brevity, this equivalence relation is referred to as the duplicate relation of the quasi-order. If there is already an equivalence relation, this construction creates again .
The minor class of is quantity
- .
Furthermore, one receives the canonical strict order on fortune
- .
Is total, then there is a strict weak order . In general, the complement of a total quasi-order is a strict weak order, and vice versa.
The following relationship exists between the original relation and the 2 induced relations:
- ,
where the two conditions on the right are mutually exclusive.
Examples:
- If you compare complex numbers based on their amount (see above), then two numbers are equivalent if and only if their amount is equal. The equivalence classes are therefore the circles around the zero point in the complex plane . A number is “smaller” than a second if it lies on the circle with a smaller radius (radius 0 is permitted).
- With the quasi-order given by a directed graph (see above), two nodes are equivalent if and only if they are the same or lie on a common cycle. It also applies if there is a directed path from to , but no directed path from to . The three equivalence classes in the graph opposite are also the following applies to the induced strict partial order:
- The divisibility relation is also a quasi-order on every integrity ring . Two elements are equivalent (in the sense of the quasi-order) if and only if they are associated , i.e. if they emerge from one another through multiplication with a unit .
Quotient set
On the quotient set or factor set ( i.e. the set of equivalence classes ) the canonical partial order is obtained through the well-defined definition
(the class of with is designated).
If the given quasi-order is total, then the result is a total order .
Examples:
- When comparing complex numbers on the basis of their absolute value (see above), the partial order on the quotient set is isomorphic to the usual (total) order on the non-negative real numbers .
- With the divisibility relation on the whole numbers (see above) the partial order on the quotient set is isomorphic to the divisibility relation on the set of natural numbers (including 0).
reflection
A quasi-order can be mirrored :
- (see also inverse relation ).
Usually you then use the notation:
- .
If the given quasi-order is total, then the result is also total.
If it is a partial order, so is the result.
The reflection of the reflection is the original.
Composition (composition, cascading)
Composition by component
On two quasi-ordered sets and the composition component-wise-less than-or-equal to the set of pairs can be defined as follows:
The composition is again a quasi-order.
Asymmetry is retained. Totality is lost, however, that is, with two total quasi-orders only one quasi-order remains, with two total orders only one partial order remains. (Example: (1,0) is not comparable to (0,1).)
There is a kind of communitativity because is isomorphic to .
Lexicographical composition
For two quasi-ordered sets and the lexicographical composition on the set of pairs is defined as follows:
The composition is again a quasi-order.
If the given quasi-orders are all total (on their respective component sets) and only then does a total quasi-order arise again. If they are all partial orders, a partial order arises again; if they are total orders, a total order arises again.
The following quasi-orders for symbol sequences ( words ) of variable length can be derived according to the lexicographical principle. To do this, be quasi-ordered and let and be the lengths of two words
- ( Kleenesche shell of )
and be .
- Then through is quasi-ordered, whereby for the sake of simplicity the order of the words of the same length is written for and for . M. a. .W .: If the smallest index is with then the following also applies to the empty word as all non-empty words. The order put together in this way is again called lexicographical. It corresponds to the composition of just the same components .
- Another composition with very similar order-theoretical properties is the quasi-lexicographical one with analogous signs for the order of words of equal length.
Associativity
The compositions are associative , that is, and .
Remarks:
- In the spreadsheet programs , a "column" corresponds to a set of components . The sorting function often offered in these programs corresponds to a lexicographical composition with a precedence of the columns to be specified, whereby there is usually a "standard" order for each column, which is a total (required for sorting!) Quasi-order. The "ascending" or "descending" sort order can be selected.
- If the individual columns are sorted in a stable manner, then the overall sorting can be broken down into individual sortings in the reverse order.
Archetype of an order relation
Let be a non-empty set, a quasi-ordered set and an arbitrary map. Then can fortune
the set can be quasi-ordered.
It is totally quasi-ordered, and that's how it is .
If is a partial order, then a partial order is if and only if is injective .
Comment:
- The international Unicode standard has existed for the digital coding of alphabets since 1991, and it seems to be gaining increasing acceptance. This does not say too much about the arrangement of the characters, since in addition to special problems such as umlauts, for example, attention / disregard of upper / lower case and special characters can make the image non- injective.
extension
If there is a quasi-order and any non-empty set, the set can be expanded as follows :
- .
How is also a quasi-order.
If total, the result is again a total quasi-order.
Antisymmetry is generally lost, that is, if the given quasi-order is a partial order (or total order), the result is only again a partial order (or total order) if it consists of exactly one element. If there are several elements, the result is only a quasi-order (or total quasi-order).
is the quasi-order (with the trivial order on ). It can be thought of as a comparison function that operates on its key fields in . The order of results can therefore be referred to again with without any loss of accuracy .
Composition on the base quantity
If you have several quasi-orders on a set , you can form the lexicographical compositions according to similar to the above
- .
They form a (non-commutative) semigroup with the (both sides) neutral element .
is a refinement of . This also means that a quasi-order that follows a ( completely total) total order does not change anything.
Example:
- Let the set of natural numbers, with the (non-injective) Euler's function and the usual smaller relation, then order the total order
the payment 2, 3, 4, 5, 6, 7, 8th, 9, 10, 11, 12 around to 2, 3, 4, 6, 5, 8th, 10, 12, 7, 9, 11 because of 1, 2, 2, 2, 4, 4, 4, 4, 6, 6, 10 for the values.
Restriction of a quasi-order
In an obvious way, the restriction to a subset is formed by a quasi-order .
Comment:
- The domains of definition are usually conceptually infinite sets. In this respect, statements about the properties of the order relationships (especially about transitivity) can only come from mathematical considerations. The assignments in the IT applications are of course always finite.
Intervals
Similar to numbers, a concept of interval can be introduced more generally for quasi-ordered sets - in a notation that is familiar from school:
Then the duplicate class of is .
For improper intervals there are the notations:
Footnotes
- ↑ in English quasi-lexicographic , radix , length-plus-lexicographic or shortlex order






































![[x] \ leq [y]: \ Longleftrightarrow x \ lesssim y](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a64b1545ba3a91986b09fbe028c625251cd49c2)

![[x] \](https://wikimedia.org/api/rest_v1/media/math/render/svg/086d16124d9131b037289469080580d905cd6e80)





























































![[from]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)



![{(} a, b {]}: = \, {]} a, b {]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b977d2fc54e47c7b77c0e74e0123b1304276d1e5)

![(a, b): = \, {]} a, b {[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa5c24babc0e38cf235f954e8222156ccdfbdbe3)

![{\ bar a} = [a, a] =: [a]](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ac1f5d2e7f50b3dd44d2e1ebaab92027e9ffd65)


![(a, \;) \,: = \, {]} a, \; {[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71451f782de539e8bdc331a61971aea46632e110)

![{(} \ ;, a {]} \;: = \, {]} \ ;, a {]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c32b4dd20a9e9a10fe21a943dbd7a817d6dd04c9)

![(\ ;, a) \,: = \, {]} \ ;, a {[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/426f0f39c27e3256bba1d4e0e3b8df8a3cef9141)
