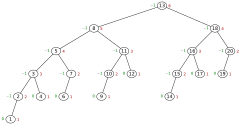
Fibonacci tree

The Fibonacci tree is the subject of graph theory , but above all a data structure in computer science . It represents a special case of the AVL tree , namely the AVL tree with the smallest number of nodes for a given height . The name suggests that Fibonacci trees, similar to Fibonacci numbers , can be defined recursively .

If you remove any node of a Fibonacci tree, from the third level onwards a tree is created that is no longer a Fibonacci tree. In the example below, it is no longer an AVL tree, if z. B. a 1 that is not the left one is removed.

As with the Fibonacci numbers, the number of   the golden section is a kind of "base of the logarithm"   . The ideal basis for a binary tree would of course be to maintain more stringent balance criteria, e.g. B. the height balance in a fully balanced binary tree , but is so complex after modifications to the tree that on average the total costs of such trees are higher, unless the application is extremely dominated by searching. The AVL criterion appears to be an attractive compromise. ${\displaystyle \Phi :={\tfrac {1+{\sqrt {5}}}{2}}\approx 1{,}618034}$ ${\displaystyle 2}$

Level 6 Fibonacci tree with balance factors (green) and height information (red)

Fibonacci trees are used as extreme cases and objects of comparison when considering the efficiency of height-balanced trees , especially AVL trees.

Recursive definition

The recursive definition is done like this:

• The level 0 Fibonacci tree is the empty tree . ${\displaystyle F_{0}}$
• The level 1 Fibonacci tree is a tree that consists of only one node . ${\displaystyle F_{1}}$
• A Fibonacci tree of level (with ) consists of a root whose left child is a Fibonacci tree of level and whose right child is a Fibonacci tree of level . ${\displaystyle F_{h}}$ ${\displaystyle h}$ ${\displaystyle h\geq 2}$ ${\displaystyle h-1}$ ${\displaystyle h-2}$

properties

• All internal nodes (nodes that are not leaves) have a balance factor of –1.
• The Fibonacci tree of level (with ) has the height . ${\displaystyle F_{h}}$ ${\displaystyle h}$ ${\displaystyle h\geq 0}$ ${\displaystyle h}$

• If the number of nodes in the Fibonacci tree is the level , then ${\displaystyle n_{h}}$ ${\displaystyle h}$

  ${\displaystyle n_{0}=0}$

  ${\displaystyle n_{1}=1}$

  ${\displaystyle n_{h}=1+n_{h-1}+n_{h-2}}$ For ${\displaystyle h\geq 2}$

• If the number of leaf nodes of the Fibonacci tree is the level , then applies ${\displaystyle b_{h}}$ ${\displaystyle h}$

  ${\displaystyle b_{0}=0}$

  ${\displaystyle b_{1}=1}$

  ${\displaystyle b_{h}=b_{h-1}+b_{h-2}}$ For ${\displaystyle h\geq 2}$

• If the number of insertion points ( half leaves ; 1 leaf = 2 half leaves) of the Fibonacci tree is the level , then applies ${\displaystyle e_{h}}$ ${\displaystyle h}$

  ${\displaystyle e_{0}=1}$

  ${\displaystyle e_{1}=2}$

  ${\displaystyle e_{h}=e_{h-1}+e_{h-2}}$ For ${\displaystyle h\geq 2}$

• With the help of the designation for the -th Fibonacci number , these quantities can also be expressed as follows: ${\displaystyle f_{h}}$ ${\displaystyle h}$

  ${\displaystyle n_{h}=f_{h+2}-1}$

  ${\displaystyle b_{h}=f_{h}}$

  ${\displaystyle e_{h}=f_{h+2}=n_{h}+1}$

(For every directed binary tree .) ${\displaystyle e=n+1}$

• At a given height, a Fibonacci tree corresponds to an AVL tree with the minimum number of nodes, so it is the worst balanced.

• According to Moivre-Binet's formula is the number of nodes

${\displaystyle n_{h}}$	${\displaystyle =f_{h+2}}$			${\displaystyle -1}$
	${\displaystyle ={\tfrac {1}{\sqrt {5}}}{\biggl [}{\biggr .}}$	${\displaystyle \left({\tfrac {1+{\sqrt {5}}}{2}}\right)^{h+2}}$	${\displaystyle -{\biggl .}\left({\tfrac {1-{\sqrt {5}}}{2}}\right)^{h+2}{\biggr ]}}$	${\displaystyle -1}$
	${\displaystyle \geqq }$	${\displaystyle {\tfrac {\Phi ^{h+2}}{\sqrt {5}}}}$	${\displaystyle -{\tfrac {(-\Phi ^{-1})^{4}}{\sqrt {5}}}}$	${\displaystyle -1}$   for and ${\displaystyle h\geq 1}$
	${\displaystyle \geqq }$	${\displaystyle {\tfrac {\Phi ^{h+2}}{\sqrt {5}}}}$		${\displaystyle -2}$   for . ${\displaystyle h\geq 0}$

• This allows the height to be estimated depending on the number of nodes ${\displaystyle h}$ ${\displaystyle n\geq 1}$

${\displaystyle h}$	${\displaystyle \leqq c\log _{2}(n+d)+b}$
	${\displaystyle \leqq c\log _{2}(n+2)+b}$

with    ,     and   . ${\displaystyle c:={\tfrac {1}{\log _{2}\Phi }}\approx 1{,}440420}$ ${\displaystyle b:={\tfrac {c}{2}}\log _{2}5-2\approx -0{,}327724}$ ${\displaystyle d:={\tfrac {1}{\Phi ^{4}{\sqrt {5}}}}+1\approx 1{,}065248}$

Other thinnest AVL trees

If you swap the left child with the right child at a node, a thinnest AVL tree is created again. This gives the number of thinnest AVL trees the height ${\displaystyle a_{h}}$ ${\displaystyle h}$

a 0 =	1
a 1 =	1
a h =	( a h –1 • a h –2 )	• 2		(for h ≥ 2)
	( h –1 left & h –2 right)	+ vice versa

That is in closed form , which is great for function ${\displaystyle a_{h}=2^{f_{h+1}-1}}$ ${\displaystyle h\to \infty }$

${\displaystyle 2^{\Phi ^{h+f}-1}}$

with approximates. ${\displaystyle f:=1-{\tfrac {\log _{\Phi }5}{2}}\approx -0{,}672276}$

The number of all AVL trees of the height can be calculated as follows: ${\displaystyle A_{h}}$ ${\displaystyle h}$

A 0 =	1
A 1 =	1
A h =	( A h –1 • A h –2 )	• 2	+ ( A h –1 • A h –1 )	(for h ≥ 2)
	( h –1 left & h –2 right)	+ vice versa	+ ( h -1 left & h -1 right)

It is the sequence A029758 in OEIS , which is for the function ${\displaystyle h\to \infty }$

${\displaystyle k^{2^{h}}=2^{2^{h+K}}}$

with or approximates. ${\displaystyle k:=k_{\mathsf {A029758}}\approx 1{,}436873}$ ${\displaystyle K:=\log _{2}{\log _{2}{k}}\approx -0{,}935305}$

Both sequences are double exponential, but with different exponents - with the result that the thinnest trees with increasing tree height are proportionally rapidly (double exponential) rare.

It follows that the number of nodes for the left and right subtree can be very different. For example, an AVL tree of height 32-4 = 28 can in the extreme case have a branch with 2 ²⁷ -1 = 134217727 ( complete binary tree of height 27) on the left and one with (Fibonacci tree of height 26) node on the right, which is a node ratio from 134217727/514227 ≈ 261 results. At a height of 64-5 = 59, we arrive with 2 ⁵⁸ -1 = 288230376151711743 and n ₅₇ = 1548008755918 to a ratio of about 186,194th ${\displaystyle n_{26}=514227}$

Search depth

The search depth of a node is the number of edges from the root to the node. For an external node in a binary search tree , it corresponds to the number of comparisons required; for internal nodes, the latter is 1 higher.

Maximum and minimum search depth of an external node

The maximum search depth of an external node in a Fibonacci tree is with as the height. ${\displaystyle h}$ ${\displaystyle h}$

2 Fibonacci trees of black depth 3

The minimum search depth of an external node in a Fibonacci tree is . Proof: The two external leaves of a tree of height 1 have search depth 1. The right external leaf of a Fibonacci tree of height 2 has search depth 1. In the recursive composition of a Fibonacci tree of height from one of height and one of height is found the minimum search depth in the subtree of the height . Hence the claim follows. ■ ${\displaystyle \lceil {\tfrac {h}{2}}\rceil }$



${\displaystyle h}$ ${\displaystyle h-1}$ ${\displaystyle h-2}$ ${\displaystyle h-2}$

Since the relationship between the maximum and minimum search depth is in red-black trees , the Fibonacci trees can be colored with the colors red and black according to the rules of the red-black tree. ${\displaystyle <2}$

Path length sum and mean search depth

The sum of the search depths over all internal nodes of the Fibonacci tree of the level , in the notation of the section Search depths and path length sums , can be recursively calculated as follows: ${\displaystyle s_{h}:=\sum _{x\in F_{h}}a(x)}$ ${\displaystyle a(x)}$ ${\displaystyle x}$ ${\displaystyle F_{h}}$ ${\displaystyle h}$ ${\displaystyle S_{\mathfrak {e}}^{F_{h}}}$

${\displaystyle s_{0}}$	${\displaystyle =}$	${\displaystyle 0}$
		(empty search tree)
${\displaystyle s_{1}}$	${\displaystyle =}$	${\displaystyle 1}$
		(only root)
${\displaystyle s_{h}}$	${\displaystyle =}$	${\displaystyle 1}$	${\displaystyle +}$	${\displaystyle s_{h-1}+n_{h-1}}$	${\displaystyle +}$	${\displaystyle s_{h-2}+n_{h-2}}$
		(new root)		(left child)		(right child)
	${\displaystyle =}$	${\displaystyle n_{h}+s_{h-1}+s_{h-2}}$
	${\displaystyle =}$	${\displaystyle f_{h+2}-1+s_{h-1}+s_{h-2}}$				for h ≥ 2.

This is satisfied by

${\displaystyle {\begin{aligned}s_{h}&=\left[h\left(3f_{h+2}+f_{h+1}\right)-2f_{h+2}-3f_{h+1}+5\right]/5\\&=\left[\left(4h-5\right)f_{h+1}+\left(3h-2\right)f_{h}+5\right]/5\end{aligned}}}$.

Proof:

${\displaystyle f_{h+2}-1+s_{h-1}+s_{h-2}}$

${\displaystyle \quad =f_{h+2}-1+\left[(h-1)\left(3f_{h+1}+f_{h}\right)-2f_{h+1}-3f_{h}+5+(h-2)\left(3f_{h}+f_{h-1}\right)-2f_{h}-3f_{h-1}+5\right]/5}$

${\displaystyle \quad =\left[5f_{h+2}+h\left(3f_{h+1}+f_{h}\right)-3f_{h+1}-f_{h}-2f_{h+1}-5f_{h}+h\left(3f_{h}+f_{h-1}\right)-6f_{h}-2f_{h-1}-3f_{h-1}+5\right]/5}$

${\displaystyle \quad =\left[h\left(3f_{h+1}+4f_{h}+f_{h-1}\right)+5f_{h+2}-5f_{h+1}-12f_{h}-5f_{h-1}+5\right]/5}$

${\displaystyle \quad =\left[h\left(3f_{h+1}+4f_{h}+f_{h+1}-f_{h}\right)+5f_{h+2}-5f_{h+1}-12f_{h}-5f_{h+1}+5f_{h}+5\right]/5}$

${\displaystyle \quad =\left[h\left(4f_{h+1}+3f_{h}\right)+5f_{h+2}-10f_{h+1}-7f_{h}+5\right]/5}$

${\displaystyle \quad =\left[h\left(4f_{h+1}+3f_{h+2}-3f_{h+1}\right)+5f_{h+2}-10f_{h+1}-7f_{h+2}+7f_{h+1}+5\right]/5}$

${\displaystyle \quad =\left[h\left(3f_{h+2}+f_{h+1}\right)-2f_{h+2}-3f_{h+1}+5\right]/5}$. ■

The external path length , i.e. i. the sum of the search depths over all external nodes with the Fibonacci tree of the level is then ${\displaystyle \textstyle S_{\mathfrak {f}}^{F_{h}}:=\sum _{x\in F_{h}}b(x)}$ ${\displaystyle b(x)}$ ${\displaystyle x=(x_{j},x_{j+1})}$ ${\displaystyle 0\leqq j\leqq n}$ ${\displaystyle F_{h}}$ ${\displaystyle h}$

${\displaystyle {\begin{aligned}S_{\mathfrak {f}}^{F_{h}}&=s_{h}+n_{h}\\&=\left[h\left(3f_{h+2}+f_{h+1}\right)-2f_{h+2}-3f_{h+1}+5\right]/5+f_{h+2}-1\\&=\left[4hf_{h+1}+\left(3h+3\right)f_{h}\right]/5.\end{aligned}}}$

Thus, the sequence A067331 in OEIS . ${\displaystyle S_{\mathfrak {f}}^{F_{h}}}$

Using Moivre-Binet's formula, we can derive from this for Fibonacci trees via the mean search depth of the limit of efficiency to find existing keys for : ${\displaystyle s_{h}/n_{h}\;=\;S_{\mathfrak {e}}^{F_{h}}/n_{h}}$ ${\displaystyle v_{\mathfrak {e}}:=S_{\mathfrak {e}}^{F_{h}}/n_{h}/\log _{2}{n_{h}}}$ ${\displaystyle h\to \infty }$

${\displaystyle {\begin{aligned}v_{\mathfrak {e}}&\to h(3\Phi ^{h+2}+\Phi ^{h+1})/5/\Phi ^{h+2}/\log _{2}{n_{h}}\\&\to h(3+\Phi ^{-1})/5/\log _{2}{f_{h+2}}\\&\to h(3+\Phi -1)/5/(h+2)/\log _{2}{\Phi }\\&\to (2+\Phi )/5/\log _{2}{\Phi }\\&=(5/2+{\sqrt {5}}/2)/5/\log _{2}{\Phi }\\&=\Phi /{\sqrt {5}}/\log _{2}{\Phi }\\&\approx 1{,}042298.\end{aligned}}}$

The same value results for the limit of efficiency to determine the absence of keys. ${\displaystyle v_{\mathfrak {f}}:=S_{\mathfrak {f}}^{F_{h}}/(n_{h}+1)/\log _{2}(n_{h}+1)}$

Proportion of unbalanced nodes in AVL trees

A somewhat more differentiated recursion allows insight into the inner asymmetries of the AVL trees. Let U _{h , u , g be} the number of AVL trees of height h with u unbalanced (right or left- heavy ) and g balanced nodes (with children of the same height). Then after considerations is analogous to above

${\displaystyle U_{0,0,0}=1}$	has empty tree	h = 0, u = 0, g = 0
${\displaystyle U_{1,0,1}=1}$	has only root	h = 1, u = 0, g = 1
${\displaystyle U_{h,u,g}=\sum _{\upsilon ,\gamma }(U_{h-2,\upsilon ,\gamma }\cdot U_{h-1,u-1-\upsilon ,g-\gamma }\cdot 2+U_{h-1,\upsilon ,\gamma }\cdot U_{h-1,u-\upsilon ,g-1-\gamma })}$,

because with children of different heights there is a u-knot and with children of the same height a g-knot. The proportion of unbalanced nodes at all nodes is , and this has the multiplicity , so that the proportion averaged over all AVL trees of height h ${\displaystyle u/(u+g)}$ ${\displaystyle U_{h,u,g}}$

${\displaystyle u_{h}:=\left(\sum _{u,g}U_{h,u,g}\cdot u/(u+g)\right)/A_{h}}$

results. Because the number of all AVL trees of the height is the same as above . ${\displaystyle h}$ ${\displaystyle \textstyle A_{h}:=\sum _{u,g}U_{h,u,g}}$ ${\displaystyle A_{h}}$

Table 2 shows numerical values ​​for small . ${\displaystyle h}$

Average search depth for AVL trees

Estimation using recursion over the height

Average search depths can be calculated using the same scheme. For the sake of comparability, we choose the search depth of the external nodes (leaves), i. i. the external path length . Let the number of AVL trees be the height with external leaves and the external path length . Then ${\displaystyle P_{h,n,p}}$ ${\displaystyle h}$ ${\displaystyle n}$ ${\displaystyle p}$

${\displaystyle P_{0,1,0}=1}$		the empty tree of height 0 with 1 external leaf and external path length 0
${\displaystyle P_{1,2,2}=1}$		the tree of height 1 (root only) with 2 external leaves and external path length 2
${\displaystyle P_{h,n,p}=\sum _{\nu ,\pi }(P_{h-2,\nu ,\pi }\cdot P_{h-1,n-\nu ,p-n-\pi }\cdot 2+P_{h-1,\nu ,\pi }\cdot P_{h-1,n-\nu ,p-n-\pi })}$,

because with the recursive composition of two AVL trees, the number of external leaves increases from

n l

and

n r

on

n l + n r

=: n

and the external path length of

p l

and

p r

on

p l + p r + n

=: p ,

since the path to the root is increased by 1 for each leaf. The number of all AVL trees of the height is ${\displaystyle h}$

${\displaystyle A_{h}:=\sum _{n,p}P_{h,n,p}}$.

It's the same as above . ${\displaystyle A_{h}}$

height	Number of trees	Share bad design weighed		Number of external sheets			external path length			average lengthened delay
${\displaystyle h}$	${\displaystyle A_{h}}$	node	root	${\displaystyle {\underline {n}}_{h}}$	n h	${\displaystyle {\overline {n}}_{h}}$	${\displaystyle {\underline {p}}_{h}}$	p h	${\displaystyle {\overline {p}}_{h}}$	v h
1	1	0.000	0.00000	2	2.0000	2	2	2.0000	2	1.0000
2	3	0.333	0.66667	3	3.3333	4th	5	6.0000	8th	1.0344
3	15th	0.311	0.40000	5	6.1333	8th	12	16,533	24	1.0263
4th	315	0.303	0.28571	8th	11.467	16	25th	41,524	64	1.0260
5	108675	0.285	0.08696	13	22,470	32	50	103.34	160	1.0228
6th	11878720875	0.274	5.76e-3	21st	44.876	64	96	251.21	384	1.0194
7th	141106591 466142946875	0.269	1.83e-5	34	89.751	128	180	592.16	896	1.0167
8th	19911 070158545297 149037891328 865229296875	0.267	1,7e-10	55	179.50	256	331	1363.8	2048	1.0146
Table 2: Unbalanced Nodes and External Path Length by Height

The column Proportion of unbalanced nodes contains that of the section #Part of unbalanced nodes in AVL trees , while the column Proportion of unbalanced roots means the percentage of trees with unbalanced roots within the total of AVL trees of height . ${\displaystyle u_{h}}$ ${\displaystyle h}$

In the column v _h , the external path length is compared with the ideal (minimum) external path length , which depends on the number of nodes (see Table 3), and the height is then averaged over all AVL trees . ${\displaystyle {\underline {p}}_{n}}$ ${\displaystyle n}$ ${\displaystyle h}$

Exact calculation

The assumption of equal probabilities for all AVL tree forms is a simplification. It is true that every possible form of a binary tree can be built up through specific insertions, but there are preferred forms of the AVL trees that arise more frequently than others after rotations. If all sequences (permutations) of the insertion are considered to be equally probable, then z. For example, for the 17 AVL trees with node number 7 (see Table 3) for the balanced tree (a complete binary tree of height 3) a frequency of 2160 and for the remaining 16 (which are all Fibonacci trees of height 4) for one half had a frequency of 144 and for the other half a frequency of 216.

Bone surfactant- paid	average height	Number of trees	Share bad design -weighed		frequency		external path length			average lengthened delay
${\displaystyle n}$	h n	${\displaystyle A_{n}}$	node	root	${\displaystyle {\underline {f}}_{n}}$	${\displaystyle {\overline {f}}_{n}}$	${\displaystyle {\underline {p}}_{n}}$	p n	${\displaystyle {\overline {p}}_{n}}$	v n
1	1.00	1	0.000	0.000	1	1	2	2.00	2	1.0000
2	2.00	2	0.500	1,000	1	1	5	5.00	5	1.0000
3	2.00	1	0.000	0.000	6th	6th	8th	8.00	8th	1.0000
4th	3.00	4th	0.500	1,000	6th	6th	12	12.00	12	1.0000
5	3.00	6th	0.280	0.600	12	36	16	16.00	16	1.0000
6th	3.00	4th	0.167	0.000	144	216	20th	20.00	20th	1.0000
7th	3.57	17th	0.327	0.571	144	2160	24	24.57	25th	1.0238
8th	4.00	32	0.393	1,000	288	3240	29	29.36	30th	1.0123
9	4.00	44	0.333	0.714	3456	25920	34	34.24	35	1.0070
10	4.00	60	0.286	0.429	25056	194400	39	39.07	40	1.0018
11	4.00	70	0.249	0.117	114048	2332800	44	44.00	44	1.0000
12	4.19	184	0.267	0.193	466560	17418240	49	49.19	50	1.0039
13	4.51	476	0.311	0.509	933120	242611200	54	54.58	56	1.0108
14th	4.79	872	0.342	0.790	8823168	2774865600	59	60.10	62	1.0187
15th	4.96	1553	0.351	0.888	116173440	54979430400	64	65.72	68	1.0268
16	5.00	2720	0.340	0.776	519747840	149860238400	70	71.41	73	1.0201
17th	5.00	4288	0.324	0.609	2769500160	1978587648000	76	77.13	79	1.0149
18th	5.00	6312	0.309	0.453	60134731776	22812754464000	82	82.88	85	1.0107
19th	5.00	9004	0.296	0.295	904805406720	398794586112000	88	88.66	91	1.0075
20th	5.02	16088	0.287	0.179	5394695644800	3968960489625600	94	94.52	97	1.0056
21st	5.10	36900	0.287	0.159	10789391289600	74716118765568000	100	100.49	103	1.0049
22nd	5.22	82984	0.293	0.237	97480461657600	1134885141276480000	106	106.55	110	1.0052
23	5.38	174374	0.304	0.380	1362760719022080	28970685819518976000	112	112.71	117	1.0064
24	5.54	346048	0.315	0.543	7172727971696640	337716405039775104000	118	118.95	123	1.0080
25th	5.70	653096	0.325	0.691	70893673900600320	7478785384139059200000	124	125.26	130	1.0101
26th	5.82	1199384	0.331	0.795	990569400644966400	134732114837823140352000	130	131.63	137	1.0125
Table 3: Unbalanced nodes and external path length by insertion order

When drawing up Table 3, all sequences of insertion according to the AVL insertion algorithm were given the same weight for each node number . (Therefore the frequencies add up to n ! ). The big difference between minimum and maximum frequency resp. shows that the tree shapes that arise are very different in frequency, with the most common also having minimal external path lengths . The latter is also the reference point for the mean extension of the external path length v _n . Fibonacci trees are quite rare, but they do not necessarily have maximum external path lengths . ${\displaystyle n}$ ${\displaystyle f_{n}}$ ${\displaystyle {\underline {f}}_{n}}$ ${\displaystyle {\overline {f}}_{n}}$ ${\displaystyle {\underline {p}}_{n}}$ ${\displaystyle {\underline {p}}_{n}}$ ${\displaystyle {\overline {p}}_{n}}$

These frequencies are much more difficult to calculate than the above numbers of trees and extensions of the path length v _h , for which the AVL trees of a fixed height are assumed to be equally likely. For small trees, however, v _n and v _h differ only slightly. R. W. Floyd estimates the mean effort to determine the absence of a -th among keys , which asymptotically corresponds to a value of for v _n . ${\displaystyle P_{h,n,p}}$ ${\displaystyle h}$ ${\displaystyle n}$ ${\displaystyle (n\!+\!1\!)}$ ${\displaystyle 1{,}01\log _{2}{n}+0{,}01}$ ${\displaystyle 1{,}01}$

The columns , and are the sequences A006265, A001855, respectively. A228155 in OEIS . ${\displaystyle A_{n}}$ ${\displaystyle {\underline {p}}_{n}}$ ${\displaystyle {\overline {p}}_{n}}$

Flank depth

The left and right flank depth is the length of the path from the root to the minimum, respectively. designated to the maximum. Since an AVL tree of the same height is obtained by mirroring an AVL tree left-right, the left and right flank depths have the same set of values. For an AVL tree of height it is at most and at least ${\displaystyle h}$ ${\displaystyle {\overline {d}}_{h}=h-1}$

${\displaystyle {\underline {d}}_{h}=\lceil {\tfrac {h}{2}}\rceil -1}$,

in accordance with the considerations for the minimum search depth of Fibonacci trees.

In a similar way as above, the left and right flank depth can be averaged over all AVL trees of the height . Let the number of AVL trees be the height with left flank depth and right flank depth . Then ${\displaystyle h}$ ${\displaystyle d_{h,l,r}}$ ${\displaystyle h}$ ${\displaystyle l}$ ${\displaystyle r}$

${\displaystyle d_{1,0,0}=1}$

${\displaystyle d_{2,1,0}=d_{2,0,1}=d_{2,1,1}=1}$

${\displaystyle d_{h,l,r}=\sum _{\lambda ,\rho }(d_{h-1,l-1,\rho }\cdot d_{h-2,\lambda ,r-1}\,+\,d_{h-2,l-1,\rho }\cdot d_{h-1,\lambda ,r-1}\,+\,d_{h-1,l-1,\rho }\cdot d_{h-1,\lambda ,r-1})}$

because with the recursive composition of two AVL trees the flank depth increases by 1 on both sides and in each of the groups “left higher”, “right higher” and “equal high” all options on the left can be combined with all options on the right and these numbers are totaled up. The following applies as a control: The number of all AVL trees of the height is ${\displaystyle h}$

${\displaystyle A_{h}:=\sum _{l,r}d_{h,l,r}}$.

It's the same as above . ${\displaystyle A_{h}}$

The mean left and right flank depth for an AVL tree of the height is then ${\displaystyle h}$

d _h  . ${\displaystyle :=\left(\sum _{l,r}l\cdot d_{h,l,r}\right)/A_{h}}$

Numerical values ​​for small are in Table 1. ${\displaystyle h}$

Average depth of descent when deleting

Similarly, an average depth of descent can be calculated which, when deleting a node, has to be descended from its height to the (half) leaves on its left or right in order to find a node that can take the place of the node to be deleted. For a single node at the height , its mean corresponds to the d _h just calculated . ${\displaystyle h}$

The mean value over all nodes of an AVL tree is, however, much lower, since most of the nodes are at a low height. Let the number of AVL trees be the height with nodes, left flank depth and flank depth sum and right flank depth and flank depth sum . Let the flank depth sum be the sum of all left resp. right flank depths of a given tree. Then ${\displaystyle D_{h,n,L,l,R,r}}$ ${\displaystyle h}$ ${\displaystyle n}$ ${\displaystyle l}$ ${\displaystyle L}$ ${\displaystyle r}$ ${\displaystyle R}$

${\displaystyle D_{1,1,0,0,0,0}=1}$		${\displaystyle \cdot }$	AVL tree with 1 node
${\displaystyle D_{2,2,1,1,0,0}=1}$		${\displaystyle /}$	AVL tree with 2 nodes on the left
${\displaystyle D_{2,2,0,0,1,1}=1}$		${\displaystyle \backslash }$	AVL tree with 2 nodes to the right
${\displaystyle D_{2,3,1,1,1,1}=1}$		${\displaystyle \wedge }$	AVL tree with 3 nodes

${\displaystyle D_{h,n,L,l,R,r}=\sum _{\lambda ,\rho ,\;\;n=n_{l}+1+n_{r}, \atop L=L_{l}+l+L_{r},\;R=R_{l}+r+R_{r}}}$	${\displaystyle (\,D_{h-1,n_{l},L_{l},l-1,R_{l},\rho }\cdot D_{h-2,n_{r},L_{r},\lambda ,R_{r},r-1}}$
	${\displaystyle +D_{h-2,n_{l},L_{l},l-1,R_{l},\rho }\cdot D_{h-1,n_{r},L_{r},\lambda ,R_{r},r-1}}$
	${\displaystyle +D_{h-1,n_{l},L_{l},l-1,R_{l},\rho }\cdot D_{h-1,n_{r},L_{r},\lambda ,R_{r},r-1\,}\,)}$

because with the recursive composition of two AVL trees, the addition of the new root increases the flank depths on both sides by 1, with the left and right flank depth sum, the related flank depth is added to the contribution of the 2 trees and in each of the groups " higher left ”,“ higher right ”and“ equal ”all options on the left are combined with all options on the right and these numbers are totaled.

The number of AVL trees of the height with nodes and the sum of the left flank depth is ${\displaystyle h}$ ${\displaystyle n}$ ${\displaystyle L}$

${\displaystyle B_{h,n,L}:=\sum _{R,l,r}D_{h,n,L,l,R,r}}$.

These trees therefore have the mean left flank depth per node . The edge depth averaged over all AVL trees of height is therefore ${\displaystyle {\frac {L}{n}}}$ ${\displaystyle h}$

${\displaystyle \Delta _{h}:=\left(\sum _{n,L}B_{h,n,L}\cdot L/n\right)/A_{h}}$.

Because we have with the same as above . ${\displaystyle \textstyle A_{h}=\sum _{n,L}B_{h,n,L}}$ ${\displaystyle A_{h}}$

Since for reasons of symmetry, the length of a path from the root to a node at a certain height in unit access probabilities does not depend on changes of direction, which is average depth of descent averaged over all the AVL trees of height likewise . ${\displaystyle h}$ ${\displaystyle \Delta _{h}}$

Some numerical values:

${\displaystyle h}$	${\displaystyle {\underline {d}}_{h}}$	d h	${\displaystyle {\overline {d}}_{h}}$	${\displaystyle \Delta _{h}}$
1	0	0	0	0
2	0	0.6667	1	0.27778
3	1	1.5333	2	0.49921
4th	1	2.4095	3	0.66886
5	2	3.3714	4th	0.79391
6th	2	4.3687	5	0.87686
7th	3	5.3686	6th	0.92801
8th	3	6.3686	7th	0.95865
9	4th	7.3686	8th	0.97660
10	4th	8.3686	9	0.98693
Table 1

The very simple consideration from the Delete section provides

${\displaystyle \lim _{h\to \infty }\Delta _{h}=1}$.

See also

• Fibonacci sequence
• Fibonacci heap

literature

• Donald E. Knuth : The Art of Computer Programming : Volume 3 Sorting and Searching . 2nd Edition. Addison-Wesley, Reading MA 1997, ISBN 0-201-89685-0 , 6.2.3 Balanced Trees.

• Kurt Mehlhorn data structures and efficient algorithms Teubner Stuttgart 1988, ISBN 3-519-12255-3 .

Individual evidence

1. ↑ The height as the maximum number of node levels or numerically the same, if there are (keyless) external leaves as with #Knuth , as the maximum number of edges from the external leaf to the root.
2. ↑ according to Knuth Theorem A, the formulation of Adelson-Velsky / Landis
3. ↑ #Knuth a. a. Cit., P. 467.
4. ^ AV Aho and NJA Sloane : Some Doubly Exponential Sequences . In: Fib. Quart., 11, Bell Laboratories Murray Hill, New Jersey . 1970, pp. 429-437.
5. ↑ external path length at #Knuth a. a. O. pp. 399-400
6. ↑ E.g. the Fibonacci tree has the external path length . The AVL tree with and has the full binary tree with 15 nodes on one side and a Fibonacci tree with 4 nodes on the other. ${\displaystyle n=20}$ ${\displaystyle p=96}$ ${\displaystyle n=20}$ ${\displaystyle p=97}$
7. ↑ With the proportions of trees with unbalanced roots, however, the different weighting becomes visible in an extreme form.
8. ↑ quoted from #Knuth a. a. Cit., P. 468
9. ↑ http://oeis.org/A006265
10. ↑ http://oeis.org/A001855
11. ↑ http://oeis.org/A228155