Fibonacci heap

In computer science , a is Fibonacci heap ( English heap , stockpile ') has a data structure similar to a binomial heap that a priority queue realized. This means that elements with a specified priority can be efficiently stored in the heap in any order and an element with the highest priority can always be removed. The priority of the elements is imprinted on them by keys . There must therefore be a total order over the set of keys , such as the less- or -equal relation (≤) over the whole numbers . Fibonacci heaps were first described in 1984 by Michael L. Fredman and Robert E. Tarjan . Its name comes from the analysis of the data structure, in which Fibonacci numbers play a major role.

Operations

Fibonacci heaps efficiently support the operations :

insert - to insert an element,
remove or delete - to remove an element,
getMin - to find the element with the minimum key,
extractMin - for returning and removing an element with a minimum key, i.e. highest priority,
decreaseKey - to decrease the key of an element and
merge or union - to merge two heaps.

Terms

All operations can be implemented with a logarithmic worst-case runtime , i.e., where n is the number of elements currently in the heap. Only the operations remove , extractMin and decreaseKey need in the worst-case linear runtime so . However, the amortized costs for almost all other operations are constant, that is . ${\ displaystyle {\ mathcal {O}} (\ log n)}$ ${\ displaystyle {\ mathcal {O}} (n)}$ ${\ displaystyle {\ mathcal {O}} (1)}$

Consequently - with amortized runtime analysis - Fibonacci heaps are superior to binary heaps or binomial heaps when executing the insert and merge operations . However, because of the poor worst-case runtime of remove , extractMin and decreaseKey, they are less suitable for online algorithms in which each individual operation must be carried out efficiently.

Comparison times :

surgery	Linear list	Sorted list	(Min) heap	Unbalanced binary tree	Fibonacci heap
insert	${\ displaystyle {\ mathcal {O}} (1)}$	${\ displaystyle {\ mathcal {O}} (n)}$	${\ displaystyle {\ mathcal {O}} (\ log n)}$	${\ displaystyle {\ mathcal {O}} (\ log n)}$ *	${\ displaystyle {\ mathcal {O}} (1)}$
getMin	${\ displaystyle {\ mathcal {O}} (n)}$	${\ displaystyle {\ mathcal {O}} (1)}$	${\ displaystyle {\ mathcal {O}} (1)}$	${\ displaystyle {\ mathcal {O}} (1)}$	${\ displaystyle {\ mathcal {O}} (1)}$
extractMin	${\ displaystyle {\ mathcal {O}} (n)}$	${\ displaystyle {\ mathcal {O}} (1)}$	${\ displaystyle {\ mathcal {O}} (\ log n)}$	${\ displaystyle {\ mathcal {O}} (1)}$	${\ displaystyle {\ mathcal {O}} (\ log n)}$ *
decreaseKey	${\ displaystyle {\ mathcal {O}} (1)}$	${\ displaystyle {\ mathcal {O}} (n)}$	${\ displaystyle {\ mathcal {O}} (\ log n)}$	${\ displaystyle {\ mathcal {O}} (\ log n)}$ *	${\ displaystyle {\ mathcal {O}} (1)}$ *
remove	${\ displaystyle {\ mathcal {O}} (n)}$	${\ displaystyle {\ mathcal {O}} (n)}$	${\ displaystyle {\ mathcal {O}} (\ log n)}$	${\ displaystyle {\ mathcal {O}} (1)}$ **	${\ displaystyle {\ mathcal {O}} (\ log n)}$ *
merge	${\ displaystyle {\ mathcal {O}} (1)}$	${\ displaystyle {\ mathcal {O}} (n + m)}$	${\ displaystyle {\ mathcal {O}} (m \ cdot \ log (n + m))}$	${\ displaystyle {\ mathcal {O}} (n + m)}$	${\ displaystyle {\ mathcal {O}} (1)}$

(*) Amortized costs
(**) If the position is known, otherwise * ${\ displaystyle {\ mathcal {O}} (\ log n)}$

Data structure

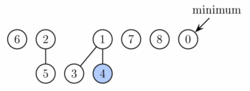
This Fibonacci heap has three trees with degrees 0, 1 and 3. Three nodes are marked. Therefore the potential of the heap is 9 (3 trees + 2 × 3 marked nodes).

A Fibonacci heap consists of a list of trees with ordered descendants, the nodes of which contain keys and possibly a marker. The priority of each node imposed by the key is at least as great as the priority of its children. This is known as the heap condition . In the min heaps shown here , the greater priority is represented by a smaller key.

Cyclic doubly linked lists are used both for the list of trees and for the lists of the child nodes in the nodes of the trees .

In addition, a pointer to the element with the highest priority, i.e. the smallest key, is managed.

A Fibonacci heap is said to be normalized when all trees have different degrees of root , i.e. H. if the roots of the trees in the list all have different numbers of child nodes.

A Fibonacci heap is a collection of trees that meet the minimum heap property, ie a child's key is always greater than or equal to the father's key. This means that the smallest key is always at the root of one of the trees. Compared to binomial heaps , the structure of a Fibonacci heap is more flexible. The trees do not have a prescribed shape, and in the extreme case the heap can have each element in a separate tree. This flexibility allows some operations to be delayed, which means that work is postponed for later operations. For example, merging heaps is done simply by concatenating the two lists of trees, and the decreaseKey operation sometimes cuts a node from its parent and creates a new tree.

At some point, however, an order must be introduced into the heap in order to achieve the desired runtime . In particular, the degree of the nodes (here degree means the number of children) is kept quite low: each node has at most the degree and the size of a subtree rooted in a node of degree k is at least F _{k + 2} , where F _{k is} the k th Fibonacci number . This is achieved by the rule that we can cut at most one child from each non-root node. When a second child is cut off, the node itself must be cut off from its parent and becomes the root of a new tree. The number of trees is reduced in the extractMin operation , in which trees are linked together. ${\ displaystyle {\ mathcal {O}} (\ log n)}$

Due to a relaxed structure, some operations can take a long time while others can run very quickly. For the amortized runtime analysis, we use the potential method by pretending that very fast processes take a little longer than they actually are. This extra time is then later combined and subtracted from the actual running time of slow operations. The time saved for later use is measured at each point in time by a potential function. The potential of a Fibonacci heap is given by potential = t + 2m .

Here t is the number of trees in the Fibonacci heap and m the number of marked nodes . A node is marked when at least one of its child nodes has been cut off because that node has been made a child of another node. All roots are not marked. The amortized running time for an operation results from the sum of the actual time and c times the potential difference, where c is a constant.

Thus, the root of each tree has a unit of time stored in a heap. This time unit can later be used to link this tree to another tree at amortized time 0. In addition, two time units are stored in each marked node . One can cut the node from its parent node. In this case the node becomes a root and the second unit of time remains stored in it as in any other root.

implementation

Operation insert

When inserting an element by means of insert is this simply as a separate tree in the list inserted of the trees and, optionally, the pointer updated to the minimum element when the key of the inserted element is smaller than that of the former minimum element. The running time is therefore constant: ${\ displaystyle {\ mathcal {O}} (1)}$

Operation merge

Merging two heaps using merge is just as easy . Here, the lists of the trees to be merged are simply linked and the pointer to the minimum element is converted, if necessary, if the key of the minimum element of the added heap is smaller than that of the previous minimum element. The running time is constant again: ${\ displaystyle {\ mathcal {O}} (1)}$

Operation decreaseKey

Fibonacci heap after reducing the key from node 9 to 0. This node and its two marked ancestors are cut out of the tree with root 1 and placed as new roots.

The decreaseKey operation is also carried out rather lazily in a Fibonacci heap: The key of the element to be updated is first set to the new value. Now it is possible that the heap property, ie all children are larger than the father, is no longer fulfilled. To restore this, you delete the updated element from the child list of its parent node and add it as a separate tree to the list of trees.

In order to avoid that the heap grows too large as a result of such operations , because extractMin would then take a long time, the condition is now set that only one child node may be removed from each node , otherwise the node itself must be from the child list its parent node can be removed ( Cut procedure ), etc. In order to realize this, the above-mentioned marking of a node appears: a node is marked precisely when it is not a node in the root list and a child has been removed from its child list. If a child whose father was marked is now removed, the Cut procedure is called recursively on the father. After careful mathematical analysis it turns out that the number of nodes in a tree of the degree , ie the root of the tree has children, is then limited downwards by the -th Fibonacci number , where is the golden ratio . This is of enormous importance for the extractMin function . ${\ displaystyle k}$ ${\ displaystyle k}$ ${\ displaystyle (k + 2)}$ ${\ displaystyle F_ {k + 2} \ geq \ varphi ^ {k}}$ ${\ displaystyle \ varphi}$ ${\ displaystyle {\ frac {1 + {\ sqrt {5}}} {2}}}$

Operation extractMin and cleanup

The node with the minimum key of 1 has been deleted and its children have been added as separate trees .

Fibonacci heap after completion of the extractMin operation . First, nodes 3 and 6 are connected to one another. Then the result is linked to the tree with root 2.

Now to the central function : extractMin . The beginning of this function is quite simple: the minimal element to which a pointer points is output, all its children are added to the root list as individual trees , and the element itself is removed from the heap . Now a new minimum has to be determined. But since none of the previous functions let the heap grow in depth, this would take a linear time. Therefore, the heap is "cleaned up" beforehand with the cleanup procedure . Then all elements of the root list are run through to find a new minimum.

The cleanup procedure : For this an array from to is initialized first. In this, after the cleanup , there should be a pointer to a tree in place if an element with a degree exists in the root list . So all elements of the root list are arranged in this array. If there is an overlap when two elements have the same degree, the element with the smaller key is made the father of the other, its degree is increased and it is sorted into the array. The above mathematical analysis ensures that there are at most elements in the array. Finally, the new root list must be built. To do this, all elements of the array are examined and merged into a list. So the running time is . ${\ displaystyle A}$ ${\ displaystyle 0}$ ${\ displaystyle 2 \ cdot \ log n}$ ${\ displaystyle d}$ ${\ displaystyle d}$ ${\ displaystyle 2 \ cdot \ log n}$ ${\ displaystyle A}$ ${\ displaystyle {\ mathcal {O}} (\ log n)}$

Operation remove

An element is removed from the heap using remove by first setting the key of the element to be removed to a value less than that of the previous minimum using decreaseKey . This will make this element the new minimal element. It can then be removed with extractMin . The term of decreaseKey is constant, by extractMin is , therefore, arises for the operation remove a maturity of likewise . ${\ displaystyle {\ mathcal {O}} (\ log n)}$ ${\ displaystyle {\ mathcal {O}} (\ log n)}$

Remarks

The operations remove and decreaseKey require that you know the position of the corresponding elements in the heap . In general, it is not possible to find an element in the heap efficiently. The insert operation must therefore return a pointer to the container for the inserted element, which the calling program remembers in a suitable place if necessary.

Applications

The Dijkstra's algorithm to find a shortest path or the Prim's algorithm for finding a minimum spanning tree in a graph with n nodes and m edges can be with Fibonacci heaps with the running time of implement. With a binary or binomial heap , only runtimes of . ${\ displaystyle {\ mathcal {O}} (n \ cdot \ log (n) + m)}$ ${\ displaystyle {\ mathcal {O}} ((n + m) \ cdot \ log (n))}$

literature

Michael L. Fredman, Robert E. Tarjan: Fibonacci heaps and their uses in improved network optimization algorithms . In: Journal of the ACM . 34, No. 3, 1987, pp. 596-615. doi : 10.1145 / 28869.28874 .

Web links

Gnarley Trees (includes animation as Java applet , also for other data structures)