Algorithm of Prim

The Prim's algorithm is used for the calculation of a minimum spanning tree in a contiguous , non-directional , edge-weighted graph .

The algorithm was developed in 1930 by the Czech mathematician Vojtěch Jarník . In 1957 it was rediscovered first by Robert C. Prim and then in 1959 by Edsger W. Dijkstra . This is why the algorithm is sometimes referred to under other names in the literature, such as the Prim-Dijkstra algorithm or algorithm by Jarnik, Prim and Dijkstra , in English-speaking countries also Jarnik's algorithm or DJP algorithm .

description

The algorithm starts with a trivial graph consisting of any node of the given graph. In each step, an edge with minimal weight is sought that connects another node . This and the corresponding node are added to. The whole thing is repeated until all nodes in are present; then a minimal spanning tree is: ${\displaystyle T}$ ${\displaystyle T}$ ${\displaystyle T}$ ${\displaystyle T}$ ${\displaystyle T}$

• Choose any node as the start graph . ${\displaystyle T}$
• As long as it does not contain all nodes: ${\displaystyle T}$
  • Select an edge of minimum weight, which is not an in nodes included with links. ${\displaystyle e}$ ${\displaystyle T}$ ${\displaystyle v}$ ${\displaystyle T}$
  • Add and to the graph . ${\displaystyle e}$ ${\displaystyle v}$ ${\displaystyle T}$

The outlined algorithm is described by the following pseudocode :

G: Graph
VG: Knotenmenge von G
w: Gewichtsfunktion für Kantenlänge
r: Startknoten (r ∈ VG)
Q: Prioritätswarteschlange
π[u]: Elternknoten von Knoten u im Spannbaum
Adj[u]: Adjazenzliste von u (alle Nachbarknoten)
wert[u]: Abstand von u zum entstehenden Spannbaum

algorithmus_von_prim(G,w,r)
01  Q  ${\displaystyle \leftarrow }$ VG   //Initialisierung
02  für alle u ∈ Q
03      wert[u]  ${\displaystyle \leftarrow }$ ∞
04      π[u]  ${\displaystyle \leftarrow }$ 0
05  wert[r]  ${\displaystyle \leftarrow }$ 0
06  solange Q ≠  ${\displaystyle \varnothing }$
07      u  ${\displaystyle \leftarrow }$ extract_min(Q)
08      für alle v ∈ Adj[u]
09          wenn v ∈ Q und w(u,v) < wert[v]
10              dann π[v]  ${\displaystyle \leftarrow }$ u
11                  wert[v]  ${\displaystyle \leftarrow }$ w(u,v)

After the algorithm ends, the minimum spanning tree is as follows:

${\displaystyle T=\left(V_{G},\lbrace \left(u,\pi [u]\right)|u\in V_{G}\backslash \lbrace r\rbrace \rbrace \right)}$

A priority queue can be used to find the lightest cut edge . The algorithm executes extractMin operations and decreaseKey operations. With a Fibonacci heap (extractMin in amortized and decreaseKey in amortized ) as the data structure results in a total run time of . ${\displaystyle |V|}$ ${\displaystyle |E|}$ ${\displaystyle O(log|V|)}$ ${\displaystyle O(1)}$ ${\displaystyle O(|E|+|V|\cdot \log |V|)}$

The loop is inherently sequential since the lightest edge in cross-section of and with the addition of a new node to may change. However, it is important for correctness that the currently lightest edge is always selected. ${\displaystyle S}$ ${\displaystyle V\setminus S}$ ${\displaystyle S}$

On a parallel random access machine with a total of processors , access to the priority queue can be accelerated at a constant time, so that the total runtime is in . Overall, the Kruskal algorithm and the Borůvka algorithm offer better parallelization approaches . ${\displaystyle O(|V|)}$ ${\displaystyle O(|E|+|V|)}$

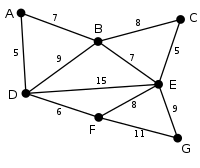
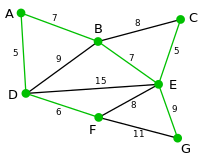
example

In this example, the sequence of Prim's algorithm is shown on a simple graph . The current tree is highlighted in green. All nodes that can be connected to the graph via a single edge in the respective step are highlighted in blue along with the respective edge with the lowest weight. The node and edge that will be added are highlighted in light blue. ${\displaystyle T}$

	This is the graph for which Prim's algorithm calculates a minimal spanning tree. The numbers at the individual edges indicate the respective edge weight.
	As the start node for the graph , the node is selected. (It could also be any other node be selected.) The start node, the node , , and in each case directly by the edges , , and are connected. Among these edges is the one with the least weight and is therefore added to the graph along with the node . ${\displaystyle T}$ ${\displaystyle D}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle E}$ ${\displaystyle F}$ ${\displaystyle DA}$ ${\displaystyle DB}$ ${\displaystyle DE}$ ${\displaystyle DF}$ ${\displaystyle DA}$ ${\displaystyle A}$ ${\displaystyle T}$
	With the existing graph , the node can be connected by the edges or , the node by the edge and the node by the edge . Among these four edges is the one with the least weight and is therefore added to the graph along with the node . ${\displaystyle T}$ ${\displaystyle B}$ ${\displaystyle AB}$ ${\displaystyle DB}$ ${\displaystyle E}$ ${\displaystyle DE}$ ${\displaystyle F}$ ${\displaystyle DF}$ ${\displaystyle DF}$ ${\displaystyle F}$ ${\displaystyle T}$
	With the existing graph , the node can be connected by the edges or , the node by the edges or and the node by the edge . Among these edges is the one with the least weight and is therefore added to the graph along with the node . ${\displaystyle T}$ ${\displaystyle B}$ ${\displaystyle AB}$ ${\displaystyle DB}$ ${\displaystyle E}$ ${\displaystyle DE}$ ${\displaystyle FE}$ ${\displaystyle G}$ ${\displaystyle FG}$ ${\displaystyle AB}$ ${\displaystyle B}$ ${\displaystyle T}$
	With the existing graph , the node can be connected by the edge , the node by the edges , or and the node by the edge . Among these edges is the one with the least weight and is therefore added to the graph along with the node . ${\displaystyle T}$ ${\displaystyle C}$ ${\displaystyle BC}$ ${\displaystyle E}$ ${\displaystyle BE}$ ${\displaystyle DE}$ ${\displaystyle FE}$ ${\displaystyle G}$ ${\displaystyle FG}$ ${\displaystyle BE}$ ${\displaystyle E}$ ${\displaystyle T}$
	With the existing graph , the node can be connected by the edges or and the node by the edges or . Among these edges is the one with the least weight and is therefore added to the graph along with the node . ${\displaystyle T}$ ${\displaystyle C}$ ${\displaystyle BC}$ ${\displaystyle EC}$ ${\displaystyle G}$ ${\displaystyle EG}$ ${\displaystyle FG}$ ${\displaystyle EC}$ ${\displaystyle C}$ ${\displaystyle T}$
	The remaining node can be connected by the edges or with the graph . Since it has the lesser weight of the two, it is added to the graph along with the node . ${\displaystyle G}$ ${\displaystyle EG}$ ${\displaystyle FG}$ ${\displaystyle T}$ ${\displaystyle EG}$ ${\displaystyle G}$ ${\displaystyle T}$
	The graph now contains all nodes of the output graph and is a minimal spanning tree of this output graph . ${\displaystyle T}$

Efficiency and running time

For an efficient implementation of Prim's algorithm, one has to find an edge that can be added to the resulting tree as easily as possible . So you need a priority queue in which all nodes are stored that do not yet belong. All nodes have a value that corresponds to the lightest edge through which the node can be connected to. If there is no such edge, the value is assigned to the node . The queue now always returns a node with the lowest value. ${\displaystyle T}$ ${\displaystyle T}$ ${\displaystyle T}$ ${\displaystyle \infty }$

The efficiency of the algorithm therefore depends on the implementation of the queue . Using a Fibonacci heap results in an optimal running time of . ${\displaystyle {\mathcal {O}}(|E|+|V|\log |V|)}$

Proof of correctness

Let be a connected , edge-weighted graph . With each iteration of the algorithm , an edge has to be found that connects a node in a subgraph with a node outside the subgraph. Because is connected, there is always a path to every node. The resulting graph of the algorithm is a tree because the edge added to the tree and the node are connected. ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle T}$

Let be a minimal spanning tree of the graph . If is equal , then is a minimal spanning tree. ${\displaystyle T_{1}}$ ${\displaystyle G}$ ${\displaystyle T_{1}}$ ${\displaystyle T}$ ${\displaystyle T}$

Otherwise, let the first edge that is added during construction of the tree that is not in the tree and be the set of nodes that were connected by the edges that were added before the edge . Then there is one node of the edge to the set of already connected nodes and the other is not. Because the tree is a spanning tree of the graph , there is a path in the tree that connects the two end nodes. When driving along the path, one must come across an edge that connects a node of the set with an edge that is not in the set . In the iteration where the edge was added to tree , the edge could now also have been added and it would be added in place of the edge if its weight were less than the weight of , and because the edge was not added we infer from that that their weight is at least as great as the weight of . ${\displaystyle e}$ ${\displaystyle T}$ ${\displaystyle T_{1}}$ ${\displaystyle V}$ ${\displaystyle e}$ ${\displaystyle e}$ ${\displaystyle V}$ ${\displaystyle T_{1}}$ ${\displaystyle G}$ ${\displaystyle T_{1}}$ ${\displaystyle f}$ ${\displaystyle V}$ ${\displaystyle V}$ ${\displaystyle e}$ ${\displaystyle T}$ ${\displaystyle f}$ ${\displaystyle e}$ ${\displaystyle e}$ ${\displaystyle f}$ ${\displaystyle e}$

Let the tree be the graph obtained by removing the edge from and adding the edge to the tree . It is easy to show that the tree is connected, has the same number of edges as the tree , and the total weight of its edges is no greater than that of Baum , therefore there is also a minimal spanning tree of the graph and it contains the edge and all edges added to the crowd during construction . If you repeat the previous steps, you finally get a minimal spanning tree of the graph that is identical to the tree . This shows that there is a minimal spanning tree. ${\displaystyle T_{2}}$ ${\displaystyle f}$ ${\displaystyle e}$ ${\displaystyle T_{1}}$ ${\displaystyle T_{2}}$ ${\displaystyle T_{1}}$ ${\displaystyle T_{1}}$ ${\displaystyle T_{2}}$ ${\displaystyle G}$ ${\displaystyle e}$ ${\displaystyle V}$ ${\displaystyle G}$ ${\displaystyle T}$ ${\displaystyle T}$

Comparison with Kruskal's algorithm

As well as the Kruskal's algorithm , which also constructs a minimum spanning tree algorithm prim is a greedy algorithm . Both algorithms start with a graph with no edges and add an edge with minimal weight in each step. They differ mainly in how the formation of a circle is avoided.

While Kruskal's algorithm looks for possible edges globally with is looking for the smallest weight and when these edges are included in the solution graph, the circle formation is active vavoids, the algorithm of Prim only considers edges that run from the nodes of the previously constructed sub-node set to nodes of the complementary set. Since an edge is selected from this set of edges, the algorithm avoids the occurrence of circles by construction.

A comparison of the runtime of the two algorithms is difficult because in Prim's algorithm the nodes determine the central complexity limit, while Kruskal's algorithm works on the basis of a sorted list of edges and its runtime is therefore dominated by the number of edges .

Parallel implementation

Graphic representation of the division of an adjacency matrix for the parallelization of Prim's algorithm. In each iteration of the algorithm, each processor updates its part of the cost vector. For this purpose, the row of the newly selected node is considered in the associated columns of the processor and then the locally optimal node be ${\displaystyle C}$Right. The results of all processors are then collected to determine the next node in the spanning tree

Prim's algorithm is fundamentally sequential in nature, as the outer loop cannot be parallelized due to data dependencies between the iterations . However, it is possible to parallelize the extract_min operation. For example, a parallel implementation of a priority queue can be used for this. On a parallel random access machine with a total of processors , access to the priority queue can be accelerated at a constant time, so that the total runtime is in . Alternatively, the nodes can be split between multiple processors so that each processor manages the incoming edges to its part of the nodes. This is shown in the following pseudocode . ${\displaystyle O(|V|)}$ ${\displaystyle O(|E|+|V|)}$

1. Assign a part of the nodes to each processor , as well as the associated (incoming) edges. When using an adjacency matrix , this corresponds to just part of the columns. ${\displaystyle P_{i}}$ ${\displaystyle V_{i}}$
2. Create a vector on each processor that contains the current costs for each node in . Initialize this vector with ${\displaystyle C}$ ${\displaystyle V_{i}}$ ${\displaystyle \infty }$
3. Repeat the following steps as long as not all nodes are included in the spanning tree:
   1. On each processor: determine the node and associated edge which has the minimum value in (local solution). ${\displaystyle v_{i}}$ ${\displaystyle e_{i}}$ ${\displaystyle C}$
   2. From the local solutions, determine the node whose connection to the current spanning tree has the lowest costs. This is possible with the help of a minimum reduction across all processors.
   3. Broadcast the selected nodes to each processor .
   4. Add the new node and the associated edge (unless it is the first node) to the spanning tree
   5. On each processor: update by looking at the edges of the newly inserted node to its own node set. ${\displaystyle C}$

This variation of Prim's algorithm can be implemented on distributed systems , on shared memory systems and on graphics processors . The running time is because entries have to be considered in each of the iterations of the algorithm . In addition, it is assumed that both the minimum reduction and the broadcast can be carried out in time. ${\displaystyle O({\tfrac {|V|^{2}}{|P|}})+O(|V|\log |P|)}$ ${\displaystyle |V|}$ ${\displaystyle {\tfrac {|V|}{|P|}}}$ ${\displaystyle O(\log |P|)}$

As a further alternative for a parallel implementation of Prim's algorithm, a variant was presented in which the sequential algorithm is executed in parallel from different start nodes. In general, other MST algorithms, such as Borůvka's algorithm , are better suited for parallelization.

literature

• Robert C. Prim : Shortest connection networks and some generalizations . In: Bell System Technical Journal , 36, 1957, pp. 1389-1401
• David Cheriton, Robert Tarjan : Finding minimum spanning trees . In: SIAM Journal on Computing , December 5, 1976, pp. 724-741
• Ellis Horowitz, Sartaj Sahni : Fundamentals of Computer Algorithms . In: Computer Science Press , 1978, pp. 174-183

Web links

Commons : Algorithm of Prim  - collection of pictures, videos and audio files

Wikibooks: Algorithm of Prim  implementations in the algorithm collection

• Interactive applet for learning, trying out and demonstrating the algorithm
• Clear presentation of the algorithm in the context of the Computer Science Year 2006
• Java applet for step-by-step visualization (English)

Individual evidence

1. ↑ Brodal, Jesper Larsson Träff, Christos D. Zaroliagis: A parallel priority queue with Constant Time Operations . In: Journal of Parallel and Distributed Computing . 49, No. 1, 1998, pp. 4-21.
2. ↑ cf. on this, for example, Ellis Horowitz, Sartaj Sahni: Fundamentals of Computer Algorithms. (see literature)
3. ↑ Brodal, Jesper Larsson Träff, Christos D. Zaroliagis: A parallel priority queue with Constant Time Operations . In: Journal of Parallel and Distributed Computing . 49, No. 1, 1998, pp. 4-21.
4. ↑ ^{a b c} Ananth Grama, Anshul Gupta, George Karypis, Vipin Kumar: Introduction to Parallel Computing 2003, ISBN 978-0-201-64865-2 , pp. 444-446.
5. ↑ Michael J. Quinn, Narsingh Deo: Parallel graph algorithms . In: ACM Computing Surveys (CSUR) 16.3 . 1984, pp. 319-348.
6. ^ Wei Wang, Yongzhong Huang, Shaozhong Guo: Design and Implementation of GPU-Based Prim's Algorithm . In: International Journal of Modern Education and Computer Science 3.4 . 2011.
7. ^ Rohit Setia: A new parallel algorithm for minimum spanning tree problem . In: Proc. International Conference on High Performance Computing (HiPC) . 2009.