Kruskal's algorithm

The Kruskal's algorithm is a greedy algorithm of graph theory for computing minimum spanning trees of undirected graphs . In addition , the graph must be connected , edge-weighted and finite.

The algorithm comes from Joseph Kruskal , who published it in 1956 in the journal "Proceedings of the American Mathematical Society ". He described him there as follows:

Carry out the following step as often as possible: Choose the shortest edge from the not yet selected edges of (the graph) that does not form a circle with the edges already selected. ${\displaystyle G}$

The shortest edge denotes the edge with the smallest edge weight. After completing the algorithm, the selected edges form a minimal spanning tree of the graph.

If the algorithm is applied to disconnected graphs, it calculates a minimal spanning tree for each connected component of the graph. These trees form a minimal spanning forest .

idea

The Kruskal's algorithm uses the county property minimum spanning trees ( English m inimum s panning t ree , MST). To do this, the edges are sorted in ascending order according to their weight in the first phase. In the second phase, iterates over the sorted edges. If an edge connects two nodes that are not yet connected by a path of previous edges, that edge is added to the MST.

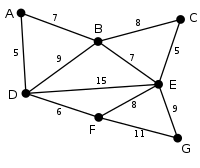
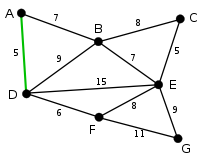
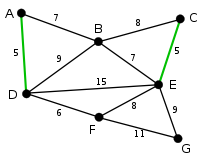
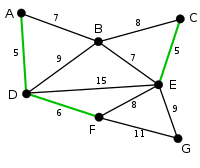
example

	This is the graph for which Kruskal's algorithm will compute a minimal spanning tree. The numbers at the individual edges indicate the respective edge weight. No edge is selected at the beginning.
	The edges AD and CE are the shortest (not yet selected) edges of the graph. Both can be selected. Here AD is selected at random. (It goes without saying that this does not form a circle in the first step.)
	Now CE is the shortest edge that has not yet been selected. Since it does not form a circle with AD, it is now selected.
	The next edge is DF with length 6. It does not form a circle with the edges already selected and is therefore selected.
	Now the edges AB and BE, each with length 7, could be selected. AB is chosen at random. The edge BD is marked in red because it would form a circle with the edges selected so far and therefore no longer needs to be taken into account in the further course of the algorithm.
	BE is now the shortest of the not yet selected edges with length 7 and since it does not form a circle with the previously selected ones, it is selected. Analogous to the edge BD in the last step, the edges BC, DE and FE are now marked in red.
	The last to be selected is the edge EG with length 9, since all shorter or equally long edges are either already selected or would form a circle. The edge FG is marked in red. Since all unselected edges would now form a circle (they are marked in red) the algorithm has reached the end and the green graph is a minimal spanning tree of the underlying graph.

Formalized algorithm

The basic idea is to traverse the edges in order of increasing edge weights and add any edge to the solution that does not form a circle with all of the previously chosen edges . So-called components are successively connected to the minimal spanning tree .

Input

A connected, edge-weighted graph is used as input . denotes the set of nodes (vertices) , the set of edges (edges) . The weight function assigns an edge weight to each edge. ${\displaystyle G=(V,\,E,\,w)}$ ${\displaystyle V}$ ${\displaystyle E}$ ${\displaystyle w\colon E\rightarrow \mathbb {R} }$

output

The algorithm provides a minimum spanning tree with . ${\displaystyle M=(V,\,E')}$ ${\displaystyle E'\subseteq E}$

algorithm

Kruskal's algorithm works non-deterministically; In other words, it may produce different results when executed repeatedly. All of these results are minimal spanning trees . ${\displaystyle G}$

An example of Kruskal's algorithm based on the Euclidean distance .

G = (V,E,w): ein zusammenhängender, ungerichteter, kantengewichteter Graph
kruskal(G)
1   ${\displaystyle E'\leftarrow \emptyset }$
2   ${\displaystyle L\leftarrow E}$
3  Sortiere die Kanten in L aufsteigend nach ihrem Kantengewicht.
4  solange  ${\displaystyle L\neq \emptyset }$
5      wähle eine Kante  ${\displaystyle e\in L}$ mit kleinstem Kantengewicht
6      entferne die Kante  ${\displaystyle e}$ aus  ${\displaystyle L}$
7      wenn der Graph  ${\displaystyle (V,E'\cup \lbrace e\rbrace )}$ keinen Kreis enthält
8          dann  ${\displaystyle E'\leftarrow E'\cup \lbrace e\rbrace }$
9  M = (V,E') ist ein minimaler Spannbaum von G.

The same algorithm can be used analogously for a maximum spanning tree. Let be a connected edge-weighted graph. Then you enter with , and in Kruskal's algorithm. Finally, the output is a minimum spanning tree of and thus a maximum of . ${\displaystyle G=(V,E,w)}$ ${\displaystyle G'=(V,E,w')}$ ${\displaystyle w'(e)=s-w(e)}$ ${\displaystyle s\in \mathbb {N} }$ ${\displaystyle \forall e\in E\,:s>w(e)}$ ${\displaystyle G'}$ ${\displaystyle G}$

A union find structure can be used to test whether nodes and are in different subtrees . Then the runtime is . Here is the time required to sort the edge weights and the inverse of the Ackermann function . For realistic entries is always less than or equal ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle O(T_{sort}(|E|)+|E|\cdot \alpha (|V|))}$ ${\displaystyle T_{sort}}$ ${\displaystyle \alpha (\cdot ))}$ ${\displaystyle \alpha (|V|)}$ ${\displaystyle 5}$

Variant 1: Parallel sorting

The sorting of the first phase can be parallelized. In the second phase, however, it is important for correctness that the edges are processed one after the other. With processors can be sorted in parallel in linear time. This reduces the total runtime . ${\displaystyle O(log|V|)}$ ${\displaystyle O(|E|\cdot \alpha (|V|))}$

Variant 2: Filter-Kruskal

A variant of Kruskal's algorithm called Filter-Kruskal was developed by Osipov et al. and is better suited for parallelization. The basic idea is to partition the edges in a similar way to Quicksort and then to sort out edges that connect nodes in the same subtree in order to reduce the costs for further sorting. Filter-Kruskal is better suited for parallelization because sorting, partitioning and filtering can easily be done in parallel by dividing the edges between the processors. The algorithm is shown in the following pseudocode.

 filterKruskal( ${\displaystyle G}$):
   falls  ${\displaystyle |E|<}$ KruskalSchwellwert:
     return kruskal( ${\displaystyle G}$)
   pivot = zufällige Kante aus  ${\displaystyle E}$
    ${\displaystyle (E_{\leq }}$,  ${\displaystyle E_{>})\gets }$partition( ${\displaystyle E}$, pivot)
    ${\displaystyle A\gets }$ filterKruskal( ${\displaystyle E_{\leq }}$)
    ${\displaystyle E_{>}\gets }$ filter( ${\displaystyle E_{>}}$)
    ${\displaystyle A\gets A}$  ${\displaystyle \cup }$ filterKruskal( ${\displaystyle E_{>}}$)
   return  ${\displaystyle A}$

 partition( ${\displaystyle E}$, pivot):
    ${\displaystyle E_{\leq }\gets \emptyset }$
    ${\displaystyle E_{>}\gets \emptyset }$
   für alle  ${\displaystyle (u,v)\in E}$:
     falls gewicht( ${\displaystyle u,v}$)  ${\displaystyle \leq }$ gewicht(pivot):
        ${\displaystyle E_{\leq }\gets E_{\leq }\cup {(u,v)}}$
     sonst
        ${\displaystyle E_{>}\gets E_{>}\cup {(u,v)}}$
   return ( ${\displaystyle E_{\leq }}$,  ${\displaystyle E_{>}}$)

 filter( ${\displaystyle E}$):
    ${\displaystyle E_{filtered}\gets \emptyset }$
   für alle  ${\displaystyle (u,v)\in E}$:
     falls find-set(u)  ${\displaystyle \neq }$ find-set(v):
        ${\displaystyle E_{filtered}\gets E_{filtered}\cup {(u,v)}}$
   return  ${\displaystyle E_{filtered}}$

Proof of correctness

Let be a connected edge-weighted graph and the output of Kruskal's algorithm. In order to prove the correctness of the algorithm, the following has to be shown: ${\displaystyle G=(V,E,w)}$ ${\displaystyle M=(V,E')}$

1. the algorithm terminates (it does not contain an infinite loop).
2. ${\displaystyle M}$is a minimal spanning tree of , so: ${\displaystyle G}$
   1. ${\displaystyle M}$is an exciting subgraph of . ${\displaystyle G}$
   2. ${\displaystyle M}$ does not contain a circle.
   3. ${\displaystyle M}$ is contiguous.
   4. ${\displaystyle M}$is minimal in terms of . ${\displaystyle G}$

The following are some ideas that demonstrate the validity of each statement:

Termination

Line 6 removes exactly one element from in each loop pass . In addition, no further operation will change it. Due to line 4, elements are only removed until . Since it was set in the algorithm at the beginning and is only finite by definition, the loop is also only run through finitely often. It follows that Kruskal's algorithm terminates. ${\displaystyle L}$ ${\displaystyle L}$ ${\displaystyle L}$ ${\displaystyle L=\emptyset }$ ${\displaystyle L=E}$ ${\displaystyle E}$

M is the spanning subgraph of G

Since the set of nodes is equal to and according to the definition of the algorithm and obviously applies because of line 8 , is the spanning subgraph of . ${\displaystyle M}$ ${\displaystyle G}$ ${\displaystyle E'\subseteq E}$ ${\displaystyle M}$ ${\displaystyle G}$

M does not contain a circle

Line 7 makes it trivial that no circle can contain. ${\displaystyle M}$

M is contiguous

In the following it is shown indirectly that is connected. Be thus not contiguous. Then there are two nodes and that are not connected by a path. But since and in are connected by a path, there is an edge in which does not exist in . The algorithm looks guaranteed in line 7 of each edge and with it . The graph in line 7 must be a circle because there is no path between and in . Line 8 is then inserted into. However, this contradicts the fact that it is not included in. Thus our assumption is invalid and yet coherent. ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle G}$ ${\displaystyle k}$ ${\displaystyle G}$ ${\displaystyle M}$ ${\displaystyle G}$ ${\displaystyle k}$ ${\displaystyle (V,E'\cup \lbrace k\rbrace )}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle M=(V,E')}$ ${\displaystyle k}$ ${\displaystyle M}$ ${\displaystyle k}$ ${\displaystyle M}$ ${\displaystyle M}$

M is minimal with respect to G.

We show by induction that the following statement is true: ${\displaystyle k=0,...,n}$

If is the set of edges that was generated in the -th step of the algorithm, then there is a minimal spanning tree that contains. The assertion is true, i.e. H. (i.e. no edge is planned yet). Every minimal spanning tree fulfills the claim and a minimal spanning tree exists, since a weighted, connected graph always has a minimal spanning tree. Now we assume that the claim for is satisfied and is the set of edges generated by the algorithm after step . Let it be the minimal spanning tree that contains. We are now looking at the case . For this, assume the last edge inserted by the algorithm. ${\displaystyle F}$ ${\displaystyle k}$ ${\displaystyle F}$ ${\displaystyle k=0}$ ${\displaystyle F=\emptyset }$ ${\displaystyle 0\leq k<n}$ ${\displaystyle F}$ ${\displaystyle k}$ ${\displaystyle M}$ ${\displaystyle F}$ ${\displaystyle k+1}$ ${\displaystyle e}$

If ${\displaystyle e\in M}$

Then the assertion is also fulfilled for, since the minimal spanning tree is extended by an edge from the minimal spanning tree . ${\displaystyle F+e}$ ${\displaystyle F}$ ${\displaystyle M}$

If ${\displaystyle e\notin M}$

Then contains a circle and there is an edge that is in the circle but not in . (If there weren't any such edge , then could n't have been added because that would have created a circle.) So that's a tree. Furthermore, the weight of cannot be less than the weight of , otherwise the algorithm would have added instead of . It follows that . But since there is a minimal spanning tree, it also applies and it follows . Thus there is a minimal spanning tree that contains and the claim is satisfied. ${\displaystyle M+e}$ ${\displaystyle f}$ ${\displaystyle F}$ ${\displaystyle f}$ ${\displaystyle e}$ ${\displaystyle F}$ ${\displaystyle M-f+e}$ ${\displaystyle f}$ ${\displaystyle e}$ ${\displaystyle f}$ ${\displaystyle e}$ ${\displaystyle w(e)\leq w(f)}$ ${\displaystyle w(M-f+e)\leq w(M)}$ ${\displaystyle M}$ ${\displaystyle w(M)\leq w(M-f+e)}$ ${\displaystyle w(M-f+e)=w(M)}$ ${\displaystyle M-f+e}$ ${\displaystyle F+e}$

This means that the Kruskal algorithm generates a set according to steps that can be expanded to a minimal spanning tree. But since the result after steps of the algorithm is already a tree (as shown above), this must be minimal. ${\displaystyle k=n}$ ${\displaystyle n}$ ${\displaystyle F}$ ${\displaystyle n}$

Time complexity

The following is the number of edges and the number of nodes. The runtime of the algorithm is made up of the necessary sorting of the edges according to their weight and checking whether the graph is circular. Sorting takes a runtime of . With a suitable implementation, checking for freedom from circles is possible more quickly, so that sorting determines the total runtime. In this respect, Prim's algorithm is more efficient, especially for graphs with many edges . ${\displaystyle \left|E\right|}$ ${\displaystyle \left|V\right|}$ ${\displaystyle {\mathcal {O}}{\bigl (}\left|E\right|\cdot \log(\left|E\right|){\bigr )}}$

If the edges are already presorted, Kruskal's algorithm works faster. Now consider how quickly it is possible to check for freedom from a circle. In order to achieve the best possible runtime, all nodes are stored in a union find structure . This contains information about which nodes are related. At the beginning, no edge is entered in the spanning tree, so each node is in a separate partition . If an edge is to be added, it is checked whether and are in different partitions. The Find (x) operation is used for this : It supplies a representative of the partition in which the node x is located. If Find ( ) and Find ( ) give different results, then the edge can be added and the partitions of the two nodes are united ( union ). Otherwise, adding the edge would create a circle, so the edge is discarded. Overall, the Find operation (for each edge) and the Union operation are called times. When using the heuristics Union-By-Size and Path Compression , an amortized runtime analysis for the algorithm results in a complexity of . Where is defined as ${\displaystyle (v_{1},v_{2})}$ ${\displaystyle v_{1}}$ ${\displaystyle v_{2}}$ ${\displaystyle v_{1}}$ ${\displaystyle v_{2}}$ ${\displaystyle 2\cdot \left|E\right|}$ ${\displaystyle \left|V\right|-1}$ ${\displaystyle {\mathcal {O}}(\left|E\right|\cdot \log ^{*}\left|V\right|)}$ ${\displaystyle \log ^{*}(n)}$

${\displaystyle \min {\Bigl \{}s\in \mathbb {N} \mid \underbrace {\log {\bigl (}\log(\ldots \log(n)\ldots ){\bigr )}} _{s{\text{-mal}}}\leq 1{\Bigr \}}}$

and practically constant. Theoretically, however, this function grows infinitely, which is why it cannot be omitted in the O notation.

Parallel implementation

Due to data dependencies between the iterations, the Kruskal algorithm is fundamentally difficult to parallelize. However, it is possible to sort the edges in parallel at the beginning or alternatively to use a parallel implementation of a binary heap in order to find the edge with the lowest weight in each iteration. By sorting in parallel, which is possible on processors in time, the runtime of the algorithm can be reduced to even with previously unsorted edges . ${\displaystyle O(n\cdot \log n)}$ ${\displaystyle O(n)}$ ${\displaystyle O(|E|\cdot \log ^{*}|V|)}$

A variant of Kruskal's algorithm called Filter-Kruskal was developed by Osipov et al. and is better suited for parallelization. The basic idea is to partition the edges in a similar way as with Quicksort and then to sort out edges that connect nodes in the same subtree in order to reduce the costs for the sorting. The algorithm is shown in the following pseudocode .

FILTER-KRUSKAL(G):
1 if |G.E| < KruskalThreshhold:
2    return KRUSKAL(G)
3 pivot = CHOOSE-RANDOM(G.E)
4  ${\displaystyle E_{<=}}$,  ${\displaystyle E_{>}}$ = PARTITION(G.E, pivot)
5 A = FILTER-KRUSKAL( ${\displaystyle E_{<=}}$)
6  ${\displaystyle E_{>}}$ = FILTER( ${\displaystyle E_{>}}$)
7 A = A ∪ FILTER-KRUSKAL( ${\displaystyle E_{>}}$)
8 return A

PARTITION(E, pivot):
1  ${\displaystyle E_{<=}}$ = ∅,  ${\displaystyle E_{>}}$ = ∅
2 foreach (u, v) in E:
3    if weight(u, v) <= pivot:
4        ${\displaystyle E_{<=}}$ =  ${\displaystyle E_{<=}}$ ∪ {(u, v)}
5    else
6        ${\displaystyle E_{>}}$ =  ${\displaystyle E_{>}}$ ∪ {(u, v)}
5 return  ${\displaystyle E_{<=}}$,  ${\displaystyle E_{>}}$

FILTER(E):
1  ${\displaystyle E_{filtered}}$ = ∅
2 foreach (u, v) in E:
3    if FIND-SET(u) ≠ FIND-SET(v):
4        ${\displaystyle E_{filtered}}$ =  ${\displaystyle E_{filtered}}$ ∪ {(u, v)}
5 return  ${\displaystyle E_{filtered}}$

Filter-Kruskal is better suited for parallelization, since sorting and partitioning, as well as filtering can simply be carried out in parallel by dividing the edges between the processors.

Further variants for a parallelization of Kruskal's algorithm are also possible. For example, there is the option of executing the sequential algorithm on several subgraphs in parallel in order to then merge them until finally only the final minimal spanning tree remains. A simpler form of the filter kruscal, in which helper threads are used to remove edges in the background that are clearly not part of the minimal spanning tree, can also be used.

Others

The algorithm was originally used by Kruskal as an aid to a simplified proof that a graph with pairwise different edge weights has a unique minimal spanning tree.

Web links

Wikibooks: Kruskal's Algorithm  - Implementations in the Algorithm Collection

• Interactive applet for learning, trying out and demonstrating the algorithm
• Ronny Harbich: Complete proof of the correctness of Kruskal's algorithm. 2006
• Clear presentation of the algorithm in the context of the computer science year 2006

Individual evidence

1. ^ Joseph Kruskal : On the shortest spanning subtree and the traveling salesman problem. In: Proceedings of the American Mathematical Society , 7, 1956, pp. 48-50
2. ↑ Vitaly Osipov, Peter Sanders, Johannes Singler: The filter-kruskal minimum spanning tree algorithm . In: Proceedings of the Eleventh Workshop on Algorithm Engineering and Experiments (ALENEX). Society for Industrial and Applied Mathematics . 2009, pp. 52-61.
3. ↑ Michael J. Quinn, Narsingh Deo: Parallel graph algorithms . In: ACM Computing Surveys (CSUR) 16.3 . 1984, pp. 319-348.
4. Jump up ↑ Ananth Grama, Anshul Gupta, George Karypis, Vipin Kumar: Introduction to Parallel Computing 2003, ISBN 978-0-201-64865-2 , pp. 412-413.
5. ↑ ^{a b} Vitaly Osipov, Peter Sanders, Johannes Singler: The filter-kruskal minimum spanning tree algorithm . In: Proceedings of the Eleventh Workshop on Algorithm Engineering and Experiments (ALENEX). Society for Industrial and Applied Mathematics . 2009, pp. 52-61.
6. ↑ Vladimir Lončar, Srdjan Škrbić, Antun Balaž: Parallelization of Minimum Spanning Tree Algorithms Using Distributed Memory Architectures . In: Transactions on Engineering Technologies. . 2014, pp. 543-554.
7. ↑ Anastasios Katsigiannis, Nikos Anastopoulos, Nikas Konstantinos, Nectarios Koziris: An approach to parallelize kruskal's algorithm using helper threads . In: Parallel and Distributed Processing Symposium Workshops & PhD Forum (IPDPSW), 2012 IEEE 26th International . 2012, pp. 1601-1610.