Statistical design of experiments
The statistical planning of experiments , in short SVP ( English design of experiments , DoE) comprises all statistical procedures that should be applied before the start of the experiment. This includes:
- the determination of the minimum test scope required to comply with the accuracy specifications
- the optimal allocation (especially in the regression analysis model I) for which the smallest scope results (D, A, G optimal test plans )
- Construction of test systems to eliminate disturbance variables ( block systems , Latin squares, etc.)
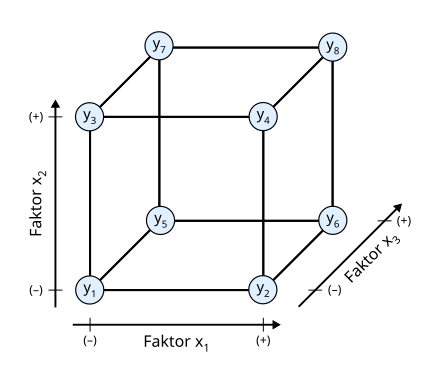
- factorial plans, especially fractional factorial plans
- sequential test planning and evaluation (sequential analysis); here data acquisition and evaluation alternate until a specified accuracy is achieved
Since experiments require resources (personnel, time, equipment, etc.), the person responsible for the experiment sees himself in a conflict between, on the one hand, the accuracy and reliability of his expected results and, on the other hand, the effort involved. In addition to material experiments, the term “experiment” also includes computer simulations . With the statistical test planning, the interrelationship between influencing factors (= independent variables) and target values (= dependent variable) is determined as precisely as possible with as few tests as possible (individual experiments) . An important part of the statistical test planning is the determination of the test scope depending on the accuracy specifications such as the risks of statistical tests and the minimally interesting minimum difference from the null hypothesis value.
history
The cornerstone of today's statistical design of experiments was laid in the 1920s by Ronald Aylmer Fisher and his team at what is now the United Kingdom's agricultural research institute Rothamsted Research . Fisher introduced basic approaches to experimentation such as repetition, random ordering, blocking, and blending. To evaluate the test results, he developed the analysis of variance . In 1935 he published his first book, The design of experiments, on the subject of experimental design , which accelerated development. In the period up to 1950, statistical test planning was primarily used in agriculture.
In 1951, the previous simple test plans by George E. P. Box and K. B. Wilson were supplemented by solution approaches for optimization tasks. There were, however, attempts to optimally plan attempts beforehand, so Kristine Smith introduced the criterion of G-optimality in her dissertation in 1918. By introducing optimization approaches, the area of application could be extended to process optimization in the chemical industry. Up to this point in time, the development of the statistical test planning was based on practical requirements and problems. In 1959, J. Kiefer was the first to present a comprehensive theoretical presentation for the construction and comparison of test plans.
Objective and benefit
The intuitive approaches in attempts like changing one factor at a time (one factor at a time) or on the principle of trial and error (trial and error), bring forth an optimal test result by chance. The individual effects and interactions of influencing factors are not recognized.
In contrast to this, statistical test planning is a methodology for the systematic planning and statistical evaluation of tests. With little effort, the functional relationship between influencing parameters and the results is determined and described mathematically. The resources required for this, such as personnel, time and costs, are known and quantifiable before the tests are carried out.
Experimental plans
| 2 4 -Experimental design | ||||
| 2 3 -Experimental design | ||||
| 2 2 -Experimental design | ||||
| Trial no. | x 1 | x 2 | x 3 | x 4 |
| 1 | - | - | - | - |
| 2 | + | - | - | - |
| 3 | - | + | - | - |
| 4th | + | + | - | - |
| 5 | - | - | + | - |
| 6th | + | - | + | - |
| 7th | - | + | + | - |
| 8th | + | + | + | - |
| 9 | - | - | - | + |
| 10 | + | - | - | + |
| 11 | - | + | - | + |
| 12 | + | + | - | + |
| 13 | - | - | + | + |
| 14th | + | - | + | + |
| 15th | - | + | + | + |
| 16 | + | + | + | + |
The test plans include systems for eliminating disturbance variables such as block systems and Latin squares, sequential test plans and factorial systems.
In contrast to the "traditional" approach, in which only one factor is varied in a test series, several factors are changed at the same time in factorial systems. So-called test plans are created that take the following into account:
- Number of factors to be examined (at least 2)
- Type of factors to be examined ( nominal (= qualitative) or quantitative )
- Existing information
- Desired accuracy / reliability of the statements
Classic plans in test planning are complete test plans , partial factor plans and test plans for effective surfaces. With screening plans, the influence of many factors can be examined simultaneously with relatively few experiments in order to identify which of the factors are statistically significant, i.e. change the output variables. With impact area plans, the connection between the few important factors and the target values can be examined in detail in order to determine the optimal settings of the factors.
Statistical experiment planning software
For the non-commercial statistics package R , a number of additional packages (the most extensive is OPDOE ) are available for planning experiments. There is special software that makes it easier for the statistically less experienced user to carry out the planning and analysis, but this is done at the expense of flexibility. Suitable programs are, for example, Design-Expert , Fusion QbD , GlobalOptimize , Modde and STAVEX; broader tools with special DoE modules are Cornerstone, JMP , Minitab , STATISTICA or Visual-XSel.
In addition, different types of simulation packages often contain specially tailored programs or modules for statistical test planning.
Examples
literature
Standard works in English
- George EP Box, J. Stuart Hunter, William G. Hunter: Statistics for Experimenters. Design, innovation, and discovery . 2nd Edition. John Wiley & Sons, Hoboken NJ 2005, ISBN 0-471-71813-0 (Wiley Series in Probability and Statistics).
- Gertrude M. Cox , William G. Cochran : Experimental Designs . 2nd Edition. Wiley, New York NY 1992, ISBN 0-471-16203-5 ( Wiley Publications in Statistics ).
- Rasch D. , Pilz, J., Gebhardt, A. and Verdooren, RL, Optimal Experimental Design with R, Boca Raton, Chapman and Hall, 2011, ISBN 978-1-4398-1697-4 (Hardback)
- Angela Dean, Daniel Voss: Design and Analysis of Experiments . Springer New York, 1999, ISBN 978-0-387-98561-9 ( Springer Texts in Statistics ).
- Douglas C. Montgomery: Design and Analysis of Experiments. International student version . 7th edition. John Wiley & Sons, Hoboken NJ 2009, ISBN 978-0-470-39882-1 .
- Raymond H. Myers, Douglas C. Montgomery, Christine M. Anderson-Cook: Response Surface Methodology. Process and Product Optimization Using Designed Experiments . 3. Edition. John Wiley & Sons, Hoboken NJ 2009, ISBN 978-0-470-17446-3 ( Wiley Series in Probability and Statistics ).
German language works
- Hans Bandemer , Andreas Bellmann: Statistical experimental planning . 4th revised edition. Teubner Verlag, Stuttgart 1994, ISBN 3-8154-2079-2 ( mathematics for engineers and natural scientists ).
- Hans Bandemer (Hrsg.): Theory and application of optimal test planning . tape 1 . Akademie-Verlag, Berlin 1977 ( Mathematical textbooks and monographs. 2nd section: Mathematical monographs 47).
- Hans Bandemer, Wolfgang Näther: Theory and application of optimal test planning . tape 2 . Akademie-Verlag, Berlin 1980 ( Mathematical textbooks and monographs. 2nd section: Mathematical monographs 48).
- Klaus Hartmann (Ed.): Statistical test planning and evaluation in the materials economy . VEB German publishing house for basic industry, Leipzig 1974.
- Dieter Rasch , G. Herrendörfer, J. Bock, N. Victor, V. Guiard: Process library for experimental planning and evaluation , 2nd improved edition in one volume with CD, R. Oldenbourg Verlag Munich Vienna 2008, ISBN 978-3-486- 58330-4
- Bernd Klein: Design of experiments - DoE. Introduction to the Taguchi / Shainin method . 2nd corrected and enlarged edition. Oldenbourg, Munich 2007, ISBN 978-3-486-58352-6 .
- Wilhelm Kleppmann: test planning . Optimize products and processes . 8th revised edition. Carl Hanser Verlag, Munich 2013, ISBN 978-3-446-43752-4 ( practical series quality knowledge ).
- Volker Nollau : Statistical Analysis. Mathematical methods of planning and evaluating experiments (= textbooks and handbooks in engineering . Volume 37 ). 2nd Edition. Birkhäuser Verlag, Basel 1979, ISBN 3-7643-1019-7 .
- Harro Petersen: Basics of statistics and statistical test planning - Part 2: Basics of statistical test planning . tape 2 . Landsberg / Lech 1991, ISBN 3-609-65340-X .
- Dieter Rasch, G. Herrendörfer, J. Bock, K. Busch: Process Library . Test planning and evaluation . tape 1-3 (1978-1981) . Deutscher Landwirtschaftsverlag, Berlin.
- Dieter Rasch, Volker Guiard, Gerd Nürnberg: Statistical experimental planning. Introduction to the methods and application of the CADEMO dialog system . G. Fischer Verlag, Stuttgart 1992, ISBN 3-437-40247-1 .
- Dieter Rasch and Dieter Schott: Mathematical Statistics, Chap. 12 test facilities. Wiley-VCH, Weinheim 2016, ISBN 978-3-527-33884-9 .
- Holger Wilker: System optimization in practice - Part 2: Guidelines for statistical test evaluation . tape 1 . Books on Demand , Norderstedt 2006, ISBN 3-8334-6306-6 .
Individual evidence
- ^ A b Eberhard Scheffler: Introduction to the practice of statistical test planning . 2nd Edition. VEB German publishing house for basic industry, Leipzig 1986, ISBN 3-342-00099-6 , p. 11 .
- ↑ Hans Bandemer , Andreas Bellmann, Wolfhart Jung, Klaus Richter: Optimal experimental planning (= mathematics and physics . Volume 131 ). Akademie-Verlag, Berlin 1973, p. 3 .
- ↑ Ulrike Groemping: CRAN Task View: Design of Experiments (DoE) & Analysis of Experimental Data. Retrieved June 9, 2015 .