Algebraic topology

from Wikipedia, the free encyclopedia

The algebraic topology is a part area of mathematics , the topological spaces (or positional relationships in the room such as in the knot theory ) by means of algebraic structures studied. It is a sub-discipline of topology .

The basic idea is to assign certain topological spaces, for example subsets of the visual space such as spheres, tori or their surfaces , certain algebraic structures such as groups or vector spaces , and this in such a way that complicated relationships on the part of the topological spaces are simplified Find the pages of the algebraic structures and thus become accessible for treatment.

Task

Simplicial complexes are made up of simple components.

A major goal of topology is to classify all topological spaces except for homeomorphism . This goal cannot be achieved in this comprehensive form. Nevertheless, effective and reliable methods are being sought with whose help certain spaces can be analyzed or even certain classes of topological spaces can be classified .

Typically, simplicial complexes , cell complexes , manifolds with and without borders are examined, i.e. spaces that are composed of topologically simple components. The images between them can be continuous , piecewise linear or differentiable images. The aim is to classify the observed spaces and the mappings between them as far as possible by means of assigned algebraic structures such as groups , rings , vector spaces and the homomorphisms (structures) between them and the quantities derived from them, down to homeomorphism or at least down to the coarser one Homotopy equivalence . For this purpose, no set-topological properties such as separation axioms or metrisability are used, but rather global properties such as “windings” or “holes” in spaces, terms that must first be specified in the context of algebraic topology.

methodology

Some results of the algebraic topology are negative in nature, such as impossibility statements. So it can be shown that there is no continuous, surjective mapping of the sphere onto the spherical surface, which leaves the spherical surface fixed in the following sense: every point of the spherical surface is mapped onto itself. Such a mapping would somehow have to create the hole that is enclosed by the spherical surface and that does not seem to be possible with a continuous mapping. A specification of these ideas leads to the homology theory . Such impossibility statements can definitely have positive consequences. For example, Brouwer's Fixed Point Theorem , according to which every continuous mapping of the sphere has a fixed point , is a simple consequence, because it can be shown that a mapping of the type just excluded could be constructed with a fixed point-free mapping of the sphere in itself.

Another typical procedure in algebraic topology is the establishment of invariants for the classification of certain topological structures. For example, if you want to classify closed continuous curves in the plane up to constant deformation (which still needs to be specified), you will find that there is only one such class, because you can clearly pull apart any such closed curve into a circle and then this then deform to the unit circle (with radius 1 around the origin of coordinates). Every closed curve is deformation-equal to the unit circle. Note that the curves are allowed to penetrate themselves; there are no nodes in the plane ( three dimensions are needed for nodes , which are also treated in algebraic topology).

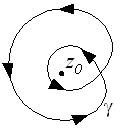
The curve circles the zero point twice.

The situation just indicated changes if the plane is replaced by the plane without the zero point. The pulling apart to form a circle no longer works because the curve can no longer pass over the zero point in the course of the deformation process. A specification of these ideas leads to the fundamental group and, more generally, to the theory of homotopy . One can consider that two closed curves belong to the same class if and only if the number of revolutions around the zero point (e.g. counterclockwise) is out of proportion. Each curve is therefore assigned a number from , namely its rotation number , and this number classifies the curves. If you limit yourself to curves that start at a fixed point and end there again because of the closed nature of the curves, you can run through two curves in a row by first going through the first curve, and then after you have arrived at the fixed starting point again is the second. The numbers in circulation add up. The addition of whole numbers on the algebraic side corresponds to the sequence of the curves on the topological side. This means that an algebraic structure, the group , is assigned to the topological space level without a zero point , and the closed curves therein are classified by an element of this group.

These considerations suggest the role of category theory in algebraic topology. The general idea is a topological situation, ie topological spaces and continuous maps between them, an algebraic situation, that is, groups, rings, or vector spaces and morphisms between them in an invariant and functorial assign manner and to draw conclusions. In this case, invariant means that isomorphic algebraic structures are assigned to homeomorphic or homotopy-equivalent spaces .

Historical development

The ancient Greek mathematicians were already concerned with deformations of three-dimensional bodies ( shearings , elongations ) and were also interested in the complexity of nodes, but the first precise concept formation that could be assigned to algebraic topology is the Euler characteristic introduced by Leonhard Euler .

In the 19th century Gauss discovered the number of links between two curves, which does not change with constant deformation without mutual penetration. The physicist Kelvin began to be interested in knots , Betti examined holes and handles in manifolds and came up with the Betti numbers named after him . Towards the end of the 19th century Poincaré classified two-dimensional manifolds (see Classification Theorem for 2-Manifolds ) and in this context introduced the fundamental concept of the fundamental group .

The first outstanding results in the algebraic topology of the 20th century were the proof of the invariance of the topological dimension by Brouwer in 1913 and the invariance of the homology , i.e. the Betti numbers, by Alexander in the 1920s. By Vietoris , Alexandrow and Čech the homology theory was extended to general spaces. Following the ideas of Poincaré and Riemann , Cartan introduced differential forms and a homology theory based on them, whose equivalence to the usual homology theory was proven by his student de Rham in the 1930s. Hurewicz generalized the concept of the fundamental group to the homotopy group . After it was established that the n-spheres have non-trivial higher homotopy groups, their determination became a central task.

At the end of the 1930s Whitney , Stiefel , Pontryagin and Chern discovered various topological invariants named after them, so-called characteristic classes , which appear as obstacles: certain things can only function or be present if these classes meet certain conditions, otherwise they pose the obstacle for it.

In the 1940s, the Morse theory became established and Eilenberg succeeded in rigorously proving the homotopy invariance of the singular homology . A further algebraization of the Poincaré duality finally led to the cohomology theory . Eilenberg and Mac Lane abstracted further to the so-called homological algebra and are considered to be the founders of category theory in this context . These considerations resulted in the Eilenberg-Steenrod uniqueness theorem .

A breakthrough in the classification of manifolds already begun by Poincaré was the surgical theory of Browder , Nowikow , Sullivan and Wall , with which a classification except for diffeomorphism of the simply connected manifolds of the dimension that are homotopy-equivalent to a given manifold succeeded.

Another important advance in the algebraic methods of topology and homology theory were Grothendieck's work on the Riemann-Roch theorem , which established the K-theory . The Bott periodicity and the Atiyah-Singer index rate in the 1960s are significant results here.

The algebraic topology is the subject of current research to this day, whereby a generally understandable representation of the results is becoming increasingly difficult. For further information, please refer to the article by Novikow given below .

In the attempt to classify three-dimensional manifolds, already undertaken by Poincaré, the problem arose of showing that every simply connected compact, unbounded 3-dimensional manifold is homeomorphic to the 3-sphere . This problem, known as the Poincaré conjecture , was only solved by Perelman in 2002 .

Applications

There are also many applications of algebraic topology outside of topology. The rotation number mentioned above is an important variable for integration paths , in function theory one speaks of zero homologous cycles as a matter of course . Methods of cohomology theory play an important role in the investigation of Riemann surfaces .

If one identifies a compact space with the algebra of continuous, complex-valued functions on what one is allowed to do according to Gelfand-Neumark's theorem , then the above concepts translate into ring theory or C * theory , at least for commutative rings or C * -Algebras, because is commutative. If the commutativity is now dropped, this leads to the so-called non-commutative topology, for example to the KK theory that goes back to Kasparov . This provides important impulses for algebra and functional analysis .

In physics , algebraic topology plays an important role in the topological quantum field theory TQFT.

literature