Morse theory
The Morse theory in the field of differential topology is a very direct access to the analysis of the topology of a manifold on the study of differentiable functions on this manifold. The American mathematician Marston Morse owes the essential insight into this .
The theory allows CW structures (or CW complexes by J. H. C. Whitehead ) and Henkel partitions (handle-decomposition) to find the variety and so information about their homology to obtain.
Before that, Arthur Cayley and James Clerk Maxwell had already gained some of these concepts by looking at topographic maps in the 19th century ( mountaineering formula ). Morse originally applied his theory to geodetic curves (critical points of the energy functional on paths). Morse code techniques were used in Raoul Bott's famous proof of his periodicity theorem for the stable homotopy groups of the unitary, orthogonal and symplectic groups.
Basic concepts
Consider a mountainous landscape for illustrative purposes M . If the height function (later called Morse function) is that assigns its height to each point, then the reverse image of a point in (the level set ) is simply a contour line . Every connected part of a contour line is either a point, a simple closed curve or a closed curve with a colon (node). Contour lines can also have higher order points (triple points, etc.), but these are unstable and can be removed by slightly deforming M. Colons in contour lines occur at saddle points (or passes ). There the surrounding contour lines run upwards and downwards in the other direction.
Now imagine if the landscape were flooded with water. If this reaches a height , the area covered by the water (the points with height ) is the same . How does the topology of the region change when the water rises? It only changes intuitively if the height of a critical point happens. This is a point where the derivative (gradient) of f disappears. In other words, the topology only changes if the water begins (1) to fill a basin (minimum), (2) to cover a saddle (mountain pass), or (3) to flood a peak (maximum).
Each of these three types of critical points - minima, maxima, saddle points - is assigned a number, the index (Morse index). Roughly speaking, this is the number of independent directions around the point at which the function f decreases. This is for minima 0, saddle points 1, maxima 2.
be defined as. A similar study of how the topology of changes as it increases can be made for a torus arranged as in the image with the projection on the vertical axis.
There are 4 critical points here and . The points and are the south and north poles of the torus, and are the south and north poles of the hole in the torus. If is less than zero, is empty. After the height of (a critical point with index 0) has passed with , is a disk, which is therefore homotopy equivalent to a point. There a 0 cell is "appended" to the empty set. If the height of (a critical point of index 1) passes with , a cylinder is homotopy equivalent to a disk with attached 1-cell (see picture on the left). If the height of (critical point with index 1) passes with , a torus from which a disk has been removed is homotopy-equivalent to a cylinder with an attached 1-cell (right picture). When it finally passes the height of (a critical point of index 2), a torus is equivalent to pinning a 2-cell.
The following rule emerges: the topology of only changes when the height of a critical point passes. If the height of a critical point with index γ passes , a γ cell is appended. If several critical points are on the same level, the situation can be resolved by considering a small disturbance of .
As it is formulated here, however, the rule is wrong. For proof, be equal to and . Then 0 is a critical point of , but the topology of does not change when zero happens. In fact, the index is poorly defined here, since the second derivatives also vanish in 0. One speaks of a degenerate critical point. When the coordinate system is rotated, the critical point is unstable - it either disappears or disintegrates into two non-degenerate critical points.
Formal development
For a real-valued smooth function on a differentiable manifold , the points on which the derivative of vanishes are called critical points of , and their images below are called critical values. If at a critical point the matrix of the second partial derivatives ( Hessian matrix ) is not singular ( i.e. it is invertible), a non- degenerate critical point is called (if the Hessian matrix is singular, degenerate analogously )
Example: For the functions
from to has a critical point at the origin for which is for non- degenerate ( is of form ) and for is degenerate ( is of form ). A less trivial example is the monkey saddle .
The index of a non-degenerate critical point of is the dimension of the largest subspace of the tangent space to at on which the Hessian matrix is negative definite. This corresponds to the intuitive definition above as the number of directions in which decreases.
The Morse Elemma
Be a non-degenerate critical point of . Then there is a map in a neighborhood of so that for everyone and
in whole . Here, α is equal to the index of at . As a corollary of the Morse elemma, it follows that the non-degenerate critical points are isolated.
Morse functions
A smooth real-valued function on a manifold is a Morse function if it has no degenerate critical points. A basic result of the Morse theory is that almost all functions are Morse functions. To put it precisely, they form a dense, open subset in the space of all smooth functions in the topology. This fact can also be described as a typical function is a Morse function or a generic function is a Morse function .
Sub-level quantities
As I said, one is interested in the question of how the topology of changes when it varies. This is partially answered by the following sentence:
- sentence
- Let it be a smooth real-valued function , let it be and be compact. If there are no critical values between and , then it is diffeomorphic to , and a deformation retract is up .
We are also interested in how the topology of changes when a critical value occurs. The following sentence applies to this:
- sentence
- Let it be a smooth real-valued function and be a non-degenerate critical point of with index . Further is and is compact and does not contain any critical points except . Then, for sufficiently small ones, the amount is homotopy-equivalent to with an appended -cell.
These results generalize and specify the (incorrect in the form there) rule from the previous section.
With the two previous results and the fact that there is a Morse function on every differentiable manifold, one can show that every differentiable manifold is a CW-complex , with a cell for each critical point with an index . To do this, you have to show that you can arrange the critical points in such a way that there is only one critical point at each critical height.
The Morse Inequalities
Morse code can be used to prove the homology of a manifold with highly restrictive propositions. The number of critical points with the index of is equal to the number of cells in the CW structure of , which are obtained by “climbing” from . Since the alternating sum of the ranks of the homology groups of a topological space is equal to the alternating sum of the ranks of the chain complex groups with which the homology is calculated, one sees that the Euler characteristic is equal to the sum
where is the number of critical points with index . It is also known from homology theory that the rank of the -th homology group of a CW complex is less than or equal to the number of cells in . The rank of the tenth homology group is therefore less than or equal to the number of critical points from the index of a Morse function . This can be specified in the Morse inequalities :
Morse code
Morse homology is defined by a generic choice of the Morse function and the Riemannian metric . The basic result is that this homology is independent of this choice, that is, an invariant of the manifold, and is isomorphic to the singular homology . It follows that the Morse numbers and (singular) Betti numbers match, which results in an immediate proof of the Morse inequalities. An infinite-dimensional version of Morse homology is as Floerhomologie known.
Edward Witten developed a further approach to Morse code theory with harmonic functions and supersymmetry in 1982.
Morse-Bott theory
The concept of the Morse function can be extended to functions with degenerate critical manifolds, that is, the core of the Hessian matrix at the critical point is equal to the tangent space of the critical submanifold. If these are points, the classic case of the Morse function results again. The index is most natural as a pair
where the dimension of the unstable manifold at a given point is the critical manifold, and is equal to plus the dimension of the critical manifold. If the Morse-Bott function is slightly disturbed, the indices of the new function lie between and on the undisturbed critical manifold.
Morse-Bott functions are useful because typical (generic) Morse functions are difficult to work with. The visualizable and easily calculable functions typically have symmetries and often lead to critical manifolds of positive dimensions. Raoul Bott used Morse code in the original proof of his periodicity theorem.
Morse code homology can also be defined for Morse-Bott functions. The differential in this homology is calculated by a spectral sequence . Frederic Bourgeois developed such an approach as part of his Morse-Bott version of symplectic field theory , which, however, was not published due to analytical problems.
literature
- Raoul Bott : Morse Theory indomitable. In: Publications Mathématiques de l'IHES. 68, 1988, p. 99, online at [1] .
- Raoul Bott: Lectures on Morse theory, old and new. In: Bulletin of the American Mathematical Society. 7, 1982, p. 331, online .
- Arthur Cayley : On Contour and Slope Line. In: The Philosophical Magazine. 18, 1859, pp. 264-268, online ( MS Word ; 38 kB).
- Yukio Matsumoto: An Introduction to Morse Theory. American Mathematical Society, Providence RI 2002, ISBN 0-8218-1022-7 ( Translations of Mathematical Monographs. 208 = Iwanami Series in modern Mathematics ).
- James Clerk Maxwell : On Hills and Dales. In: The Philosophical Magazine. 40, 1870, p. 269, online at: On Hills and Dales (PDF; 803 kB).
- J. Milnor : Morse theory. Based on Lecture Notes by M. Spivak and R. Wells. Princeton University Press, Princeton NJ 1963 ( Annals of Mathematics Studies 51, ISSN 0066-2313 ).
- John Milnor: Lectures on the h-Cobordism theorem. Princeton University Press, Princeton NJ 1965 ( Mathematical Notes 1).
- Marston Morse: The Calculus of Variations in the Large. American Mathematical Society, New York NY 1934 ( American Mathematical Society. Colloquium Publications. 18, ISSN 0065-9258 ).
- Matthias Schwarz: Morse Homology. Birkhäuser, Basel et al. 1993, ISBN 3-7643-2904-1 ( Progress in Mathematics 111).
- H. Seifert , W. Threlfall : calculus of variations in the large. (Theory of Marston Morse). = Morse theory. Teubner, Leipzig et al. 1938 ( Hamburger Mathematische Einzelschriften 24, ZDB -ID 503145-x ).





![f ^ {- 1} \ left (- \ infty, a \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6642f367a0180be349e5ddaa4743846acd14475)





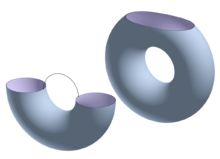

























![M ^ a = f ^ {- 1} (- \ infty, a]](https://wikimedia.org/api/rest_v1/media/math/render/svg/53abddf77935b16d17f7279fc5b8f445fc3857a2)

![f ^ {- 1} [a, b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0271b4e02a328dca4b40a34113c5dbcc74a2616f)



![f ^ {- 1} [q- \ epsilon, q + \ epsilon]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fb7ce0737e2bb5b0a2678f81195d24cd009b817)






![C ^ \ gamma -C ^ {\ gamma -1} + - \ cdots \ pm C ^ 0 \ ge {\ rm {Rank}} [H_ \ gamma (M)] - {\ rm {Rank}} [H_ { \ gamma -1} (M)] + - \ cdots \ pm {\ rm {Rank}} [H_0 (M)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/700506f209fa79ca56d4990e671d8f277b46eff8)


