Differential form

The term differential form (often also called alternating differential form) goes back to the mathematician Élie Joseph Cartan . Differential shapes are a fundamental concept of differential geometry . They allow a coordinate-independent integration on general oriented differentiable manifolds .

context

Be it ${\displaystyle U}$

• an open subset of the ${\displaystyle \mathbb {R} ^{n}}$
• or a differentiable submanifold of the ${\displaystyle \mathbb {R} ^{n}}$
• or a differentiable manifold .

In each of these cases there is

• the concept of differentiable function on the space of infinitely differentiable functions on going with designated; ${\displaystyle U;}$ ${\displaystyle U}$ ${\displaystyle C^{\infty }(U)}$
• the concept of the tangent space an at a point ${\displaystyle \mathrm {T} _{p}U}$ ${\displaystyle U}$ ${\displaystyle p\in U;}$
• the concept of the directional derivative for a tangential vector and a differentiable function ${\displaystyle {\tfrac {\partial f}{\partial X}}}$ ${\displaystyle X\in \mathrm {T} _{p}U}$ ${\displaystyle f;}$
• the concept of the differentiable vector field in the space of the vector fields is denoted by. ${\displaystyle U;}$ ${\displaystyle U}$ ${\displaystyle \Gamma (\mathrm {T} U)}$

The dual space of the tangent space is called the cotangent space . ${\displaystyle \mathrm {T} _{p}U}$ ${\displaystyle \mathrm {T} _{p}^{*}U}$

definition

Differential form

A differential form of degree on ${\displaystyle k}$ ${\displaystyle U}$ or short form is a smooth cut in th outer power of Kotangentialbündels of . In symbolic notation this means , whereby the cotangent bundle of , the th outer power of and thus the amount of the smooth sections of designated. ${\displaystyle k}$ ${\displaystyle \omega }$ ${\displaystyle k}$ ${\displaystyle U}$ ${\displaystyle \omega \in \Gamma (\Lambda ^{k}(T^{*}U))}$ ${\displaystyle T^{*}U}$ ${\displaystyle U}$ ${\displaystyle \Lambda ^{k}(T^{*}U)}$ ${\displaystyle k}$ ${\displaystyle T^{*}U}$ ${\displaystyle \Gamma (\Lambda ^{k}(T^{*}U))}$ ${\displaystyle \Lambda ^{k}(T^{*}U)}$

This means that an alternating multilinear form on the tangent space is assigned to each point ; in such a way that for smooth vector fields the function ${\displaystyle p\in U}$ ${\displaystyle \omega _{p}}$ ${\displaystyle T_{p}U}$ ${\displaystyle k}$ ${\displaystyle X_{1},\ldots ,X_{k}}$

${\displaystyle p\mapsto \omega _{p}((X_{1})_{p},\ldots ,(X_{k})_{p})\in \mathbb {R} }$

smooth , i.e. differentiable as often as desired.

Alternatively, a -form can be viewed as an alternating , smooth, multilinear map . That means: assigns a function to vector fields so that ${\displaystyle k}$ ${\displaystyle \omega }$ ${\displaystyle \omega \colon (\Gamma TU)^{k}\to C^{\infty }(U)}$ ${\displaystyle \omega }$ ${\displaystyle k}$ ${\displaystyle X_{1},\ldots ,X_{k}}$ ${\displaystyle \omega (X_{1},\ldots ,X_{k})}$

• ${\displaystyle \omega (X_{1},\ldots ,X'_{i}+X''_{i},\ldots ,X_{k})=\omega (X_{1},\ldots ,X'_{i},\ldots ,X_{k})+\omega (X_{1},\ldots ,X''_{i},\ldots ,X_{k})}$
• ${\displaystyle \omega (X_{1},\ldots ,f\cdot X_{i},\ldots ,X_{k})=f\cdot \omega (X_{1},\ldots ,X_{i},\ldots ,X_{k})}$ For ${\displaystyle f\in C^{\infty }(U),1\leq i\leq k}$

and

• ${\displaystyle \omega (X_{1},\ldots ,X_{i},\ldots ,X_{j},\ldots ,X_{k})=-\omega (X_{1},\ldots ,X_{j},\ldots ,X_{i},\ldots ,X_{k})}$

applies.

Alternative with recourse to tensor fields : A form is an alternating, covariant tensor field of the level ${\displaystyle k}$ ${\displaystyle k.}$

Space of differential forms

The set of forms forms a vector space and is denoted by. You continue to bet ${\displaystyle k}$ ${\displaystyle U}$ ${\displaystyle \Omega ^{k}(U)}$

${\displaystyle \Omega (U)=\bigoplus _{k=1}^{\infty }\Omega ^{k}(U).}$

For finite-dimensional manifolds this sum is finite, since the vector space is the zero vector space . The set is an algebra with the outer product as multiplication and thus again a vector space. From a topological point of view, this space is also a sheaf . ${\displaystyle k>\dim U}$ ${\displaystyle \Omega ^{k}(U)}$ ${\displaystyle \Omega (U)}$

One can understand it as an element of external power ; hence the outer product (i.e., the product in outer algebra ) defines maps ${\displaystyle \omega _{p}}$ ${\displaystyle \Lambda ^{k}(T_{p}^{*}U)}$ ${\displaystyle \wedge }$

${\displaystyle \Omega ^{k}(U)\times \Omega ^{\ell }(U)\to \Omega ^{k+\ell }(U),\quad (\omega ,\eta )\mapsto \omega \wedge \eta ,}$

being through ${\displaystyle \omega \wedge \eta }$

${\displaystyle (\omega \wedge \eta )_{p}=\omega _{p}\wedge \eta _{p}}$

is defined point by point.

This product is graduated-commutative , it applies

${\displaystyle \omega \wedge \eta =(-1)^{\deg \omega \cdot \deg \eta }\cdot \eta \wedge \omega ;}$

where denotes the degree of d. H. is a form, so is . Accordingly, the product of two forms of odd degree is anti-commutative and commutative in all other combinations. ${\displaystyle \deg }$  ${\displaystyle \omega }$ ${\displaystyle \omega ,}$ ${\displaystyle \omega }$ ${\displaystyle k}$ ${\displaystyle \deg }$  ${\displaystyle \omega =k}$

Examples

• Smooth functions are 0-forms.
• Pfaff's forms are 1-forms.

Coordinate representation

Let it be a -dimensional differentiable manifold. Let us also assume a local coordinate system (a map) . So is ${\displaystyle M}$ ${\displaystyle n}$ ${\displaystyle (U,x)}$

${\displaystyle B=\{\mathrm {d} x_{i_{1}}|_{p}\wedge \ldots \wedge \mathrm {d} x_{i_{k}}|_{p}\mid i_{1}<\ldots <i_{k}\}}$

a basis of where is the total differential of the -th coordinate function . That is, the linear form is on which maps the -th basis vector of the basis to 1 and all others to 0. ${\displaystyle \Lambda ^{k}(T_{p}^{*}M).}$ ${\displaystyle \mathrm {d} x_{i}}$ ${\displaystyle i}$ ${\displaystyle x_{i}}$ ${\displaystyle \mathrm {d} x_{i}|_{p}}$ ${\displaystyle T_{p}(M)}$ ${\displaystyle i}$ ${\displaystyle \textstyle {\frac {\partial }{\partial x_{1}}}|_{p},\ldots ,{\frac {\partial }{\partial x_{n}}}|_{p}}$

Every differential form has a unique representation on every map ${\displaystyle \omega \in \Omega ^{k}(M)}$ ${\displaystyle (U,x)}$

${\displaystyle \omega |_{U}=\sum _{1\leq i_{1}<\ldots <i_{k}\leq n}a_{i_{1},\ldots ,i_{k}}\,\mathrm {d} x_{i_{1}}\wedge \ldots \wedge \mathrm {d} x_{i_{k}}}$

with suitable differentiable functions ${\displaystyle a_{i_{1},\ldots ,i_{k}}.}$

The coordinate representation shows that the only differential form is for the zero form . ${\displaystyle k>n}$ ${\displaystyle \omega =0}$

External derivative

→ Main article : Outer derivative

The outer derivative is an operator that assigns a differential form to a differential form. If we consider it on the set of differential forms, i.e. on the set of smooth functions, the outer derivative corresponds to the usual derivative for functions. ${\displaystyle k}$ ${\displaystyle k+1}$ ${\displaystyle 0}$

definition

The outer derivative of a -form becomes inductive using the Lie derivative and the Cartan's formula ${\displaystyle \mathrm {d} \omega }$ ${\displaystyle k}$ ${\displaystyle \omega }$

${\displaystyle {\mathcal {L}}_{X}=i_{X}\circ \mathrm {d} +\mathrm {d} \circ i_{X}}$

Are defined; there is a vector field, the Lie derivative and the substitution of ${\displaystyle X}$ ${\displaystyle {\mathcal {L}}_{X}}$ ${\displaystyle i_{X}}$ ${\displaystyle X.}$

For example, if is a 1-form, then is ${\displaystyle \omega }$

${\displaystyle ({\mathcal {L}}_{X}\omega )(Y)={\mathcal {L}}_{X}(\omega (Y))-\omega ({\mathcal {L}}_{X}(Y))=X\omega (Y)-\omega ([X,Y])}$

and

${\displaystyle ((\mathrm {d} \circ i_{X})\omega )(Y)=(\mathrm {d} (\omega (X)))(Y)=Y\omega (X),}$

so

${\displaystyle \,\mathrm {d} \omega (X,Y)=X\omega (Y)-Y\omega (X)-\omega ([X,Y])}$

for vector fields ; the Lie bracket denotes . ${\displaystyle X,Y}$ ${\displaystyle [X,Y]}$

The general formula is

${\displaystyle {\begin{array}{rcl}\mathrm {d} \omega (X_{0},\ldots ,X_{k})&=&\sum _{i=0}^{k}(-1)^{i}X_{i}\omega (X_{0},\ldots ,{\hat {X}}_{i},\ldots ,X_{k})+\\[0.5em]&&+\sum _{0\leq i<j\leq k}(-1)^{i+j}\omega ([X_{i},X_{j}],X_{0},\ldots ,{\hat {X}}_{i},\ldots ,{\hat {X}}_{j},\ldots ,X_{k})\,;\end{array}}}$

the roof in the symbol means that the corresponding argument must be omitted. ${\displaystyle {\hat {}}}$ ${\displaystyle {\hat {X}}_{i}}$

properties

The outer derivative has the following properties:

• The external derivative is an anti-derivation . That is, is -linear, and Leibniz's rule applies to ${\displaystyle \mathrm {d} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \alpha \in \Omega ^{k}(U),\beta \in \Omega ^{l}(U)}$

${\displaystyle \mathrm {d} (\alpha \wedge \beta )=\mathrm {d} \alpha \wedge \beta +(-1)^{k}\alpha \wedge \mathrm {d} \beta .}$

• Let then the outer derivative agree with the total differential . ${\displaystyle f\in C^{\infty }(U),}$
• ${\displaystyle \mathrm {d} ^{2}=\mathrm {d} \circ \mathrm {d} =0}$
• The outer derivative respects restrictions. So let it be open and then we call the outer derivative a local operator. ${\displaystyle U\subset V\subset M}$ ${\displaystyle \alpha \in \Omega ^{k}(V).}$ ${\displaystyle \mathrm {d} (\alpha |_{U})=(\mathrm {d} \alpha )|_{U}.}$

These four properties fully characterize the external derivative. This means that the above empirical formula can be derived from these properties. If you calculate with the outer derivative, you prefer to calculate with the properties of the derivative and avoid the above formula.

Coordinate representation of the outer derivative

The outer derivative of a differential form

${\displaystyle \omega =\sum _{1\leq i_{1}<\ldots <i_{k}\leq n}a_{i_{1},\ldots ,i_{k}}(x)\cdot \mathrm {d} x_{i_{1}}\wedge \ldots \wedge \mathrm {d} x_{i_{k}}}$

in coordinate representation is

${\displaystyle \mathrm {d} \omega =\sum _{1\leq i_{1}<\ldots <i_{k}\leq n}\mathrm {d} a_{i_{1},\ldots ,i_{k}}\wedge \mathrm {d} x_{i_{1}}\wedge \ldots \wedge \mathrm {d} x_{i_{k}}.}$

with the total differentials of the coefficient functions

${\displaystyle \mathrm {d} a_{i_{1},\ldots ,i_{k}}=\sum _{j=1}^{n}{\frac {\partial a_{i_{1},\ldots ,i_{k}}}{\partial x_{j}}}\mathrm {d} x_{j}}$.

To express the resulting expressions again through the standard basis, are the identities

${\displaystyle \mathrm {d} x_{i}\wedge \mathrm {d} x_{j}=-\mathrm {d} x_{j}\wedge \mathrm {d} x_{i}}$

and

${\displaystyle \mathrm {d} x_{i}\wedge \mathrm {d} x_{i}=0}$

important.

example

for true ${\displaystyle n=2,k=1}$

${\displaystyle {\begin{aligned}\mathrm {d} (a_{1}\cdot \mathrm {d} x_{1}+a_{2}\cdot \mathrm {d} x_{2})&=\mathrm {d} a_{1}\wedge \mathrm {d} x_{1}+\mathrm {d} a_{2}\wedge \mathrm {d} x_{2}\\[0.5em]&=\left({\frac {\partial a_{1}}{\partial x_{1}}}\mathrm {d} x_{1}+{\frac {\partial a_{1}}{\partial x_{2}}}\mathrm {d} x_{2}\right)\wedge \mathrm {d} x_{1}+\left({\frac {\partial a_{2}}{\partial x_{1}}}\mathrm {d} x_{1}+{\frac {\partial a_{2}}{\partial x_{2}}}\mathrm {d} x_{2}\right)\wedge \mathrm {d} x_{2}\\[0.5em]&={\frac {\partial a_{1}}{\partial x_{1}}}\cdot \mathrm {d} x_{1}\wedge \mathrm {d} x_{1}+{\frac {\partial a_{1}}{\partial x_{2}}}\cdot \mathrm {d} x_{2}\wedge \mathrm {d} x_{1}+{\frac {\partial a_{2}}{\partial x_{1}}}\cdot \mathrm {d} x_{1}\wedge \mathrm {d} x_{2}+{\frac {\partial a_{2}}{\partial x_{2}}}\cdot \mathrm {d} x_{2}\wedge \mathrm {d} x_{2}\\[0.5em]&=\left({\frac {\partial a_{2}}{\partial x_{1}}}-{\frac {\partial a_{1}}{\partial x_{2}}}\right)\cdot \mathrm {d} x_{1}\wedge \mathrm {d} x_{2}.\end{aligned}}}$

In general, the outer derivative of a 1-form applies

${\displaystyle \mathrm {d} \left(\sum _{i=1}^{n}a_{i}\cdot \mathrm {d} x_{i}\right)=\sum _{1\leq i<j\leq n}\left({\frac {\partial a_{j}}{\partial x_{i}}}-{\frac {\partial a_{i}}{\partial x_{j}}}\right)\cdot \mathrm {d} x_{i}\wedge \mathrm {d} x_{j}}$

For , therefore, the coefficients of the outer derivative of a 1-form form the rotation of the vector formed from the coefficients of the 1-form. ${\displaystyle n=3}$

Further operations on differential forms

Inner product

Let be a smooth vector field. The inner product is a linear map ${\displaystyle X\in T(M)}$

${\displaystyle i_{X}\colon \Omega ^{k}(M)\to \Omega ^{k-1}(M),}$

by

${\displaystyle \omega \mapsto \omega (X,\cdot ,\ldots ,\cdot )}$

given is. This means that the inner product maps a shape to a shape by evaluating the shape on a fixed vector field . This mapping is an analog of the tensor taper in the space of differential forms. This is why this operation is sometimes called contraction in English. ${\displaystyle k}$ ${\displaystyle \omega }$ ${\displaystyle (k-1)}$ ${\displaystyle X}$

The inner product is an anti-derivation . That is, for and the Leibniz rule applies ${\displaystyle i_{X}}$ ${\displaystyle \omega \in \Omega ^{k}(M)}$ ${\displaystyle \nu \in \Omega ^{l}(M)}$

${\displaystyle i_{X}(\omega \wedge \nu )=(i_{X}\omega )\wedge \nu +(-1)^{k}\omega \wedge (i_{X}\nu ).}$

Also applies to the inner product ${\displaystyle i_{X}\circ i_{X}=0.}$

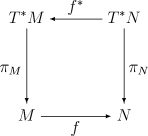
Back transport (pullback) of differential forms

→ Main article : return transport

Scheme of a pull-back, is the cotangent bundle of the manifold and corresponding for ${\displaystyle T^{*}M}$ ${\displaystyle M}$ ${\displaystyle N}$

If there is a smooth mapping between differentiable manifolds , then for the form retrieved using is defined as follows: ${\displaystyle f\colon M\to N}$ ${\displaystyle \omega \in \Omega ^{k}(N)}$ ${\displaystyle f}$  ${\displaystyle (f^{*}\omega )\in \Omega ^{k}(M)}$

${\displaystyle (f^{*}\omega )(X_{1},\ldots ,X_{k}):=\omega (\mathrm {d} f(X_{1}),\ldots ,\mathrm {d} f(X_{k}))\,.}$

It is caused by induced map of the derivatives , known as "push-forward" called. Withdrawal is compatible with the external drain and external product: ${\displaystyle df\colon TM\to TN}$ ${\displaystyle f}$

• ${\displaystyle f^{*}(\mathrm {d} \omega )=\mathrm {d} (f^{*}\omega )}$

(written in more detail: on the left , against it on the right ) and ${\displaystyle \mathrm {d} =\mathrm {d} ^{(N)}}$ ${\displaystyle \mathrm {d} =\mathrm {d} ^{(M)}}$

• ${\displaystyle f^{*}(\omega \wedge \eta )=(f^{*}\omega )\wedge (f^{*}\eta )}$

for all ${\displaystyle \omega ,\eta \in \Omega ^{pback}(N)}$

In particular, mapping between the De Rham cohomology groups (see below) ${\displaystyle f}$

${\displaystyle f^{pback}\colon \mathrm {H} _{\mathrm {dR} }^{k}(N)\longrightarrow \mathrm {H} _{\mathrm {dR} }^{k}(M),}$

Pay attention to the reversal of the arrow direction opposite (“pull-back”, “cohomology” instead of “homology”). ${\displaystyle f\colon M\to N}$

Dual form and star operator

→ Main article : Hodge star operator

Outer forms are considered in a -dimensional space in which an inner product (metric) is defined, so that an orthonormal basis of the space can be formed. The form dual to an external form of degree in this -dimensional space is a -form ${\displaystyle n}$ ${\displaystyle e_{i}}$ ${\displaystyle k}$ ${\displaystyle n}$ ${\displaystyle (n-k)}$

${\displaystyle *(e_{1}\wedge e_{2}\wedge \ldots \wedge e_{k})=e_{k+1}\wedge e_{k+2}\wedge \ldots \wedge e_{n}.}$

Both sides are written in an oriented form. Formally, the dual form is designated by using the (Hodge) operator. Especially for differential forms in three-dimensional Euclidean space we get: ${\displaystyle *}$

${\displaystyle *\mathrm {d} x=\mathrm {d} y\wedge \mathrm {d} z}$

${\displaystyle *\mathrm {d} y=\mathrm {d} z\wedge \mathrm {d} x}$

${\displaystyle *\mathrm {d} z=\mathrm {d} x\wedge \mathrm {d} y}$

with the 1 forms . It was taken into account that the oriented order is here and (cyclical interchanges in ). ${\displaystyle dx,dy,dz}$ ${\displaystyle (y,z),(x,y)}$ ${\displaystyle (z,x)}$ ${\displaystyle (x,y,z)}$

The symbol is intended to underline the fact that there is an inner product in the space of forms on an underlying space , because it is possible to write for two forms and as a volume form and the integral ${\displaystyle *}$ ${\displaystyle M}$ ${\displaystyle \alpha \wedge *\beta }$ ${\displaystyle k}$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$

${\displaystyle (\alpha ,\beta )=\int _{M}\alpha \wedge *\beta }$

returns a real number. The addition dual indicates that the double application to a -form results in the -form again - except for the sign , which must be considered separately. More precisely, for a -form in a -dimensional space, the metric of which has the signature ( in Euclidean space, in Minkowski space): ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle n}$ ${\displaystyle s}$ ${\displaystyle s=+1}$ ${\displaystyle s=-1}$

${\displaystyle **\alpha =(-1)^{k(n-k)}s\;\alpha }$

Above it was shown how in 3-dimensional Euclidean space the 2-form results with the external derivation of a 1-form with the components of the rotation vector of the vector analysis as coefficients. These two form you can use the -operator now formally directly as one form ( red vector) write: . Similarly, the operator is used to “translate” the Stokes theorem formulated above into vector analysis form. ${\displaystyle \alpha }$ ${\displaystyle d\wedge \alpha }$ ${\displaystyle *}$ ${\displaystyle *(d\wedge \alpha )}$ ${\displaystyle *}$

De Rham cohomology

→ Main article : De Rham cohomology

A coquette complex can be constructed from graduated algebra together with the outer derivative . For this is then compared with the usual methods of homological algebra one cohomology defined. Georges de Rham was able to show that this cohomology theory named after him agrees with the singular cohomology . In order to define the De Rham cohomology, the terms of the exact and the closed differential form are defined first: ${\displaystyle \Omega (U)}$

Exact and closed forms

A -form is called closed if holds; it is called exact if there is a -form such that holds. Because of the formula , every exact shape is closed. Note that closeness, in contrast to exactness, is a local property: If there is an open cover of then a -form is closed if and only if the restriction of on is closed for each . ${\displaystyle k}$ ${\displaystyle \omega }$ ${\displaystyle \mathrm {d} \omega =0}$ ${\displaystyle (k-1)}$ ${\displaystyle \eta }$ ${\displaystyle \omega =\mathrm {d} \eta }$ ${\displaystyle \mathrm {d} \mathrm {d} \eta =0}$ ${\displaystyle \{V_{\alpha }\}}$ ${\displaystyle U,}$ ${\displaystyle k}$ ${\displaystyle \omega }$ ${\displaystyle \omega }$ ${\displaystyle V_{\alpha }}$ ${\displaystyle \alpha }$

The De Rham cohomology groups

The factor space

{closed forms on } {exact forms on } ${\displaystyle k}$ ${\displaystyle U}$ ${\displaystyle {\big /}}$ ${\displaystyle k}$ ${\displaystyle U}$

is called -th De Rham cohomology group It contains information about the global topological structure of ${\displaystyle k}$ ${\displaystyle \mathrm {H} _{\mathrm {dR} }^{k}(U).}$ ${\displaystyle U.}$

Poincaré's lemma

→ Main article : Poincaré lemma

The Poincaré lemma says that for and star regions . More generally, the statement of this lemma applies to contractible open subsets of The proof is constructive, i. H. explicit examples are constructed, which is very important for applications. Note that consists of the locally constant functions , since by definition there are no exact 0-forms. So it's for everyone ${\displaystyle \mathrm {H} _{\mathrm {dR} }^{k}(U)=0}$ ${\displaystyle k>0}$ ${\displaystyle U}$ ${\displaystyle U}$ ${\displaystyle \mathbb {R} ^{n}.}$ ${\displaystyle \mathrm {H} _{\mathrm {dR} }^{0}(U)}$ ${\displaystyle \mathrm {H} _{\mathrm {dR} }^{0}(U)\not =0}$ ${\displaystyle U\not =\varnothing .}$

If it is closed and exact, it follows ${\displaystyle \omega }$ ${\displaystyle \eta =\mathrm {d} \eta '}$

${\displaystyle \omega \wedge \eta =\omega \wedge \mathrm {d} \eta '=(-1)^{\deg \omega }\mathrm {d} (\omega \wedge \eta ')\,.}$

The same applies if is exact and closed. So there are induced mappings ${\displaystyle \omega }$ ${\displaystyle \eta }$

${\displaystyle \mathrm {H} _{\mathrm {dR} }^{k}(U)\times H_{\mathrm {dR} }^{m}(U)\longrightarrow \mathrm {H} _{\mathrm {dR} }^{k+m}(U).}$

An example from electrodynamics

In electrodynamics which implies Lemma of Poincaré that to each pair of electromagnetic fields, to a two-step alternating differential form in a four-dimensional Minkowski space can be summarized, a single-stage vector potential form with exists, a so-called "four-potential", see also four-vector . Current and charge densities can also be combined into a four-vector or a corresponding 3-form . ${\displaystyle {\vec {E}},{\vec {B}}}$ ${\displaystyle \mathbf {F} }$ ${\displaystyle \mathbf {A} }$ ${\displaystyle \mathbf {F} =\mathrm {d} \mathbf {A} }$ ${\displaystyle \mathbf {j} }$

The relativistic Maxwell equations of electrodynamics on a four-dimensional space-time manifold (with metric and determinant of the metric , whereby here of course the signature of a Minkowski space is present, for example for according to the definition of the line element ) are, for example, using this symbolism: ${\displaystyle M}$ ${\displaystyle g_{\alpha ,\beta }}$ ${\displaystyle g}$ ${\displaystyle \mathrm {diag} (+1,-1,-1,-1)}$ ${\displaystyle \alpha =0,1,2,3,}$ ${\displaystyle \mathrm {ds} }$

${\displaystyle \mathrm {d} \mathbf {F} =2(\partial _{\gamma }F_{\alpha \beta }+\partial _{\beta }F_{\gamma \alpha }+\partial _{\alpha }F_{\beta \gamma })\mathrm {d} \,x^{\alpha }\wedge \mathrm {d} \,x^{\beta }\wedge \mathrm {d} \,x^{\gamma }=0}$

(the so-called Bianchi identity ) and

${\displaystyle \mathrm {d} (*\mathbf {F} )={F^{\alpha \beta }}_{;\alpha }{\sqrt {-g}}\,\epsilon _{\beta \gamma \delta \eta }\mathrm {d} \,x^{\gamma }\wedge \mathrm {d} \,x^{\delta }\wedge \mathrm {d} \,x^{\eta }=\mathbf {j} }$

with the electromagnetic field tensor expressed as a 2-form

${\displaystyle \mathbf {F} =F_{\alpha \beta }\,\mathrm {d} \,x^{\alpha }\wedge \mathrm {d} \,x^{\beta }\,,}$

z. B. with the z-component of the vector of magnetic induction and with the current (written as 3-form) ${\displaystyle F_{1,2}=B_{z}}$

${\displaystyle \mathbf {j} =j^{\alpha }{\sqrt {-g}}\,\epsilon _{\alpha \beta \gamma \delta }\mathrm {d} \,x^{\beta }\wedge \mathrm {d} \,x^{\gamma }\wedge \mathrm {d} \,x^{\delta }.}$

Here is the anti-symmetrization symbol ( Levi-Civita symbol ), and the semicolon stands for the covariant derivative . As usual, double occurring indices are added ( Einstein's sum convention ) and natural units are used (speed of light replaced by ). Using the -operator, the second set of the four Maxwell equations can alternatively be written with a 1-form for the current. From the Maxwell equations one can see that and in electrodynamics obey very different equations, so the duality is not a symmetry of this theory. This is because the duality interchanges electrical and magnetic fields, but in electrodynamics no magnetic monopoles are known. In contrast , the free Maxwell equations that result for have dual symmetry. ${\displaystyle \epsilon _{\alpha \beta \gamma \delta }}$ ${\displaystyle c}$ ${\displaystyle 1}$ ${\displaystyle *}$ ${\displaystyle \mathbf {F} }$ ${\displaystyle *\mathbf {F} }$ ${\displaystyle \mathbf {j} \equiv 0}$

The potential form is only unambiguous except for one additive addition : and result in the same with a calibration form that is fulfilled but otherwise arbitrary. You can use this additional so-called calibration freedom to meet additional constraints point by point. In electrodynamics, for example, it is required that the additional so-called Lorenz condition ( Lorenz calibration ) should apply everywhere ; in the four components this condition is simple . This "calibration fixation" finally results in the so-called "retarded potential" as a unique solution of all four Maxwell equations: ${\displaystyle \mathbf {A} }$ ${\displaystyle \mathrm {d} \chi }$ ${\displaystyle \mathbf {A} }$ ${\displaystyle \mathbf {A} +\mathrm {d} \chi }$ ${\displaystyle \mathbf {F} ,}$ ${\displaystyle \chi }$ ${\displaystyle \mathrm {d} (\mathrm {d} \chi )\equiv 0}$ ${\displaystyle \mathbf {A} }$ ${\displaystyle \mathrm {d} (*\mathbf {A} )=0}$ ${\displaystyle \partial _{\nu }A^{\nu }=0}$

${\displaystyle A^{\nu }(\mathbf {r} ,t)=\int \,{\frac {j^{\nu }(\mathbf {r'} ,t-{\frac {|\mathbf {r} -\mathbf {r'} |}{c}})}{4\pi |\mathbf {r} -\mathbf {r'} |}}\,\mathrm {d} ^{3}r'\,}$

When making the transition to the dual, it should be noted that you are not dealing with the one but with the one who has a different metric, namely the Minkowski metric . The line element invariant in Lorentz transformations is where the differential is the proper time and the sum convention was used. Co- and contravariant four-vector components now differ. Although but ${\displaystyle \mathbb {R} ^{4},}$ ${\displaystyle \mathbb {M} ^{4}}$ ${\displaystyle \mathrm {d} s^{2}=-c^{2}\mathrm {d} \tau ^{2}=dx^{2}+dy^{2}+dz^{2}-c^{2}dt^{2}=-\mathrm {d} x_{\nu }\mathrm {d} x^{\nu },}$ ${\displaystyle \mathrm {d} \tau }$ ${\displaystyle +\mathrm {d} x_{0}\equiv +\mathrm {d} x^{0}=c\,dt,}$ ${\displaystyle -\mathrm {d} x_{1}\equiv +\mathrm {d} x^{1}=dx,\,\,-\mathrm {d} x_{2}\equiv +\mathrm {d} x^{2}=dy,\,\,-\mathrm {d} x_{3}\equiv +\mathrm {d} x^{3}=dz.}$

Integration theory

orientation

→ Main article : Orientation (mathematics)

If this is the name of a -form on which no point disappears, an orientation on together with such a form is called oriented. An orientation defines orientations of the tangential and cotangent spaces: A base of the cotangent space at a point is positively oriented if ${\displaystyle n=\dim U,}$ ${\displaystyle n}$ ${\displaystyle U,}$ ${\displaystyle U.}$ ${\displaystyle U}$ ${\displaystyle \alpha }$ ${\displaystyle \eta _{1},\ldots ,\eta _{n}}$ ${\displaystyle p}$

${\displaystyle \alpha _{p}=a\cdot \eta _{1}\wedge \ldots \wedge \eta _{n}}$

with a positive number applies; a base of the tangent space at a point is positively oriented if ${\displaystyle a}$ ${\displaystyle X_{1},\ldots ,X_{n}}$ ${\displaystyle p}$

${\displaystyle \alpha (X_{1},\ldots ,X_{n})>0}$

applies.

Two orientations are said to be equivalent if they differ only by an universally positive factor; this condition is equivalent to defining the same orientation on every tangent or cotangent space.

If connected , there are either no or exactly two equivalence classes. ${\displaystyle U}$

${\displaystyle U}$means orientable if an orientation of exists. ${\displaystyle U}$

Integration of differential forms

Let it be again and we assume that an orientation has been chosen. Then there is a canonical integral ${\displaystyle n=\dim U,}$ ${\displaystyle U}$

${\displaystyle \int _{U}\omega }$

for -forms is an open subset of and the standard coordinate functions im and is ${\displaystyle n}$ ${\displaystyle \omega .}$ ${\displaystyle U}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle x_{1},\ldots ,x_{n}}$ ${\displaystyle \mathbb {R} ^{n}}$

${\displaystyle \omega =f\,\,\mathrm {d} x_{1}\wedge \ldots \wedge \mathrm {d} x_{n},}$

so applies

${\displaystyle \int _{U}\omega =\int _{U}f(x_{1},\dots ,x_{n})\,\,\mathrm {d} x_{1}\ldots \mathrm {d} x_{n};}$

the integral on the right is the ordinary Lebesgue integral im ${\displaystyle \mathbb {R} ^{n}.}$

If a -dimensional oriented manifold is open and a map, then one defines ${\displaystyle M}$ ${\displaystyle n}$ ${\displaystyle U\subset M}$ ${\displaystyle \phi \colon U\to \mathbb {R} ^{n}}$

${\displaystyle \int _{U}\omega =\int _{\phi (U)}(\phi ^{-1})^{*}\omega }$

as an integral of the -form over a map area . The differential form is therefore brought back to the open subset with the parameterization of and then integrated according to the above definition. From the transformation theorem it follows that this definition is invariant to coordinate changes. ${\displaystyle n}$ ${\displaystyle \omega }$ ${\displaystyle U}$ ${\displaystyle \omega }$ ${\displaystyle \phi ^{-1}\colon \phi (U)\to U}$ ${\displaystyle U}$ ${\displaystyle \phi (U)\subset \mathbb {R} ^{n}}$

If, more generally, is a measurable subset of , then one defines ${\displaystyle B}$ ${\displaystyle U}$

${\displaystyle \int _{B}\omega =\int _{U}\chi _{B}\omega }$

with the characteristic function , d. H. is set outside of zero. ${\displaystyle \chi _{B}}$ ${\displaystyle \omega }$ ${\displaystyle B}$

A decomposition can be used to define the integral over the whole ${\displaystyle M}$

${\displaystyle M=\bigcup _{j=1}^{\infty }M_{j}}$

can be selected in a countable number of pairwise disjoint measurable subsets , so that each is completely contained in one map area. So you bet ${\displaystyle M_{j}}$ ${\displaystyle M_{j}}$ ${\displaystyle U_{j}}$

${\displaystyle \int _{M}\omega =\sum _{j=1}^{\infty }\int _{M_{j}}\omega }$.

The following transformation theorem applies to integrals of differential forms: If is an orientation- preserving diffeomorphism , then applies to ${\displaystyle f\colon M\to N}$ ${\displaystyle \omega \in \Omega ^{n}(N)}$

${\displaystyle \int _{N}\omega =\int _{M}f^{*}\omega }$

with the on retrieved form . ${\displaystyle M}$ ${\displaystyle f^{*}\omega }$

Stokes' theorem

→ Main article : Stokes theorem

If a compact, oriented -dimensional differentiable manifold is bordered and provided with the induced orientation, then holds for every -form ${\displaystyle M}$ ${\displaystyle n}$ ${\displaystyle \partial M}$ ${\displaystyle \partial M}$ ${\displaystyle (n-1)}$ ${\displaystyle \omega }$

${\displaystyle \int _{M}\mathrm {d} \omega =\int _{\partial M}\omega .}$

This theorem is a far-reaching generalization of the main theorem of differential and integral calculus . It contains the Gaussian integral theorem and the classical integral theorem by Stokes as special cases .

Is closed , that is, for every exact -Fform d follows . H. for the relationship: ${\displaystyle M}$ ${\displaystyle \partial M=\emptyset ,}$ ${\displaystyle n}$ ${\displaystyle \omega ^{\text{exakt}},}$ ${\displaystyle \omega \equiv \omega ^{\text{exakt}}=\mathrm {d} \varphi ,}$

${\displaystyle \int _{M}\omega ^{\text{exakt}}=\int _{M}\mathrm {d} \varphi =\int _{\partial M=\emptyset }\varphi =0\,}$

To clarify the mentioned property of one often uses the formulation with a circle integral: ${\displaystyle M}$

${\displaystyle \oint _{M}\omega ^{\text{exakt}}=0}$

The integral provides a map

${\displaystyle \mathrm {H} _{\mathrm {dR} }^{n}(M)\to \mathbb {R} .}$

If connected , this mapping is an isomorphism . This brings you back to the De Rham cohomology (see above). ${\displaystyle M}$

Sample calculations

On the Cartesian coordinates are the 1-form ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle (x,y,z)}$

${\displaystyle \omega =z^{2}\,\mathrm {d} x+2y\,\mathrm {d} y+xz\,\mathrm {d} z}$

and the 2-form

${\displaystyle \nu =z\,\mathrm {d} z\wedge \mathrm {d} x}$

given.

The following applies to the outer product

${\displaystyle \omega \wedge \nu =z^{3}\,\underbrace {\mathrm {d} x\wedge \mathrm {d} z\wedge \mathrm {d} x} _{=\,0}+2yz\,\underbrace {\mathrm {d} y\wedge \mathrm {d} z\wedge \mathrm {d} x} _{=\,\mathrm {d} x\wedge \mathrm {d} y\wedge \mathrm {d} z}+xz^{2}\,\underbrace {\mathrm {d} z\wedge \mathrm {d} z\wedge \mathrm {d} x} _{=\,0}=2yz\,\mathrm {d} x\wedge \mathrm {d} y\wedge \mathrm {d} z}$.

The outer derivative of gives ${\displaystyle \omega }$

${\displaystyle \mathrm {d} \omega =2z\,\mathrm {d} z\wedge \mathrm {d} x+2\,\mathrm {d} y\wedge \mathrm {d} y+(z\,\mathrm {d} x+x\,\mathrm {d} z)\wedge \mathrm {d} z=2z\,\mathrm {d} z\wedge \mathrm {d} x-z\,\mathrm {d} z\wedge \mathrm {d} x=z\,\mathrm {d} z\wedge \mathrm {d} x}$,

so . In particular, it is exact and therefore closed, i.e. H. . This can be verified by direct calculation: . ${\displaystyle \mathrm {d} \omega =\nu }$ ${\displaystyle \nu }$ ${\displaystyle \mathrm {d} \nu =0}$ ${\displaystyle \mathrm {d} \nu =\mathrm {d} z\wedge \mathrm {d} z\wedge \mathrm {d} x=0}$

Is further given by , followed by , , and , , for on retrieved form: ${\displaystyle c\colon [0,1]\to \mathbb {R} ^{3}}$ ${\displaystyle c(t)=(t^{2},2t,1)}$ ${\displaystyle x=t^{2}}$ ${\displaystyle y=2t}$ ${\displaystyle z=1}$ ${\displaystyle \mathrm {d} x=2t\,\mathrm {d} t}$ ${\displaystyle \mathrm {d} y=2\,\mathrm {d} t}$ ${\displaystyle \mathrm {d} z=0}$ ${\displaystyle [0,1]}$

${\displaystyle c^{*}\omega =2t\,\mathrm {d} t+8t\,\mathrm {d} t=10t\,\mathrm {d} t}$.

For the integral of over the curve im given by thus results ${\displaystyle \omega }$ ${\displaystyle c}$ ${\displaystyle \Gamma =c([0,1])}$ ${\displaystyle \mathbb {R} ^{3}}$

${\displaystyle \int _{\Gamma }\omega =\int _{[0,1]}c^{*}\omega =\int _{0}^{1}10t\,\mathrm {d} t=5}$.

If the unit sphere is in , then the edge of the unit sphere is , therefore . According to Stokes' theorem, because of ${\displaystyle S^{2}=\{\mathbf {x} \in \mathbb {R} ^{3}:\|\mathbf {x} \|_{2}=1\}}$ ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle S^{2}}$ ${\displaystyle B^{3}=\{\mathbf {x} \in \mathbb {R} ^{3}:\|\mathbf {x} \|_{2}<1\}}$ ${\displaystyle S^{2}=\partial B^{3}}$ ${\displaystyle \mathrm {d} \nu =0}$

${\displaystyle \int _{S^{2}}\nu =\int _{B^{3}}\mathrm {d} \nu =0}$.

The 3-shape can be integrated, for example, via the unit cube . Its integral agrees with the Lebesgue integral of the coefficient function : ${\displaystyle \omega \wedge \nu }$ ${\displaystyle W=[0,1]^{3}}$ ${\displaystyle (x,y,z)\mapsto 2yz}$

${\displaystyle \int _{W}\omega \wedge \nu =\int _{W}2yz\,\mathrm {d} x\wedge \mathrm {d} y\wedge \mathrm {d} z=\int _{0}^{1}\int _{0}^{1}\int _{0}^{1}2yz\,\mathrm {d} x\,\mathrm {d} y\,\mathrm {d} z=2\cdot \int _{0}^{1}y\,\mathrm {d} y\cdot \int _{0}^{1}z\,\mathrm {d} z={\frac {1}{2}}}$.

Complex differential forms

→ Main article : Complex differential form

In the theory of complex differential forms, the calculus introduced here is applied to complex manifolds . This works largely in the same way as the definition of the forms described here. However, analogous to the complex numbers, the spaces of the complex differential forms are converted into two spaces of (real) differential forms

${\displaystyle {\mathcal {E}}^{r}(M)\cong \Omega ^{r,r}(M)=\Omega ^{r}(M)\oplus i\Omega ^{r}(M)}$

disassembled. The space is then called the space of forms. Analogous to the outer derivative, two new derivatives can be defined on these spaces. These are Dolbeault - called and Dolbeault cross operator, and similar to the De Rham cohomology can be a means of Dolbeault cross-operator again cohomology form. This is called Dolbeault cohomology . ${\displaystyle \Omega ^{p,q}}$ ${\displaystyle (p,q)}$

literature

• Herbert Amann, Joachim Escher : Analysis III. 2nd Edition. Birkhäuser, Basel 2008, ISBN 978-3-7643-8883-6 , Chapters XI and XII.
• Henri Cartan : Differential Forms. Bibliographisches Institut, Mannheim 1974, ISBN 3-411-01443-1
• Klaus Jänich : Vector analysis. 5th edition. Springer, Berlin / Heidelberg 2005, ISBN 978-3-540-27338-7 .
• Shigeyuki Morita: Geometry of differential forms. American Mathematical Society 2001, ISBN 0821810456 .
• Harley Flanders : Differential forms with applications to the physical sciences. Academic Press 1963.
• Harold Edwards : Advanced Calculus - a differential forms approach. Birkhäuser 1994 (first 1969).
• Steven H. Weintraub : Differential Forms a complement to vector calculus. Academic Press 1997.

Web links

• Gunnar Floystad, Exterior Algebra and central notions in mathematics, Notices AMS, Volume 62, 2015, No. 4, pdf
• Differential form in nLab