Apollonian problem

Figure 1: A solution (pink) to the Apollonios problem. The given circles are shown in black.

Figure 2: Example of three circles (black) and the associated eight solution circles

The Apollonian problem ( problem of Apollonios ) is one of the most famous problems of ancient geometry . It is a matter of constructing the circles with a compass and ruler that touch any three given circles. Apollonios von Perge (* approx. 265 BC; † approx. 190 BC) dedicates a book that has not survived to this problem ( On Touching ).

Since one can also assume an infinitely small radius and an infinitely large radius for the starting circles, not only three circles, but also points and straight lines ( tangents ) can be assumed. There are a total of ten possible combinations for the given pieces, which are listed below.

Since the complete solution of the problems solves all design cases touching (tangent) of circles, dots and lines, of course, the Berührkreise are at the triangle containing ( Ankreis , inscribed circle , radius ).

history

A rich repertoire of geometrical and algebraic methods has been developed to solve the Apollonian problem, which has been called "the most famous of all geometrical problems". The original approach of Apollonios has been lost, but François Viète and others have developed reconstructions based on indications in the description by Pappos . The first new solution method was published in 1596 by Adriaan van Roomen , who found the centers of the solution circles as the intersection of two hyperbolas . Van Roomen's method was refined in 1687 by Isaac Newton in his Principia and by John Casey in 1881.

Despite the successful solution to the Apollonius problem, van Roomen's method has a disadvantage. A valued property in classical Euclidean geometry is the ability to solve problems exclusively with compasses and ruler . Many constructions are impossible when limited to these aids, for example the angle trisection . However, many of these "impossible" problems can be solved by intersecting curves such as hyperbolas, ellipses, and parabolas ( conic sections ). For example, cube doubling (the problem of constructing a cube with twice the volume of a given cube) cannot be solved with a compass and ruler, but Menaichmus showed that the solution can be found by intersecting two parabolas. Therefore, based on the solution by van Roomen - which was based on the intersection of two hyperbolas - it was not possible to decide whether a construction with compass and ruler is possible.

Van Roomen's friend François Viète , who originally got van Roomen to deal with the Apollonian problem, developed a method that used only compasses and ruler. Before Viète's solution appeared, Regiomontanus had doubts about the possibility of a construction with compass and ruler. Viète first solved some simple special cases of the Apollonios problem, such as the determination of a circle through three given points, which only has one solution if the points are different. Building on this, he solved more complicated special cases, in some cases by reducing or enlarging the given circles. According to the fourth-century account of Pappos of Alexandria , the original work by Apollonios on the problem - entitled Ἐπαφαί ( Epaphaí , "touches"; Latin: De tactionibus , De contactibus ) - followed a similar progressive approach. Viète's solution is therefore regarded as a plausible reconstruction of Apollonios' solution, even if further reconstructions were published independently by three different authors.

Various other geometric solutions to the Apollonios problem were developed in the 19th century. The most notable solutions are those of Jean-Victor Poncelet (1811) and Joseph Diaz Gergonne (1814). While Poncelet's proof is based on similarity centers of circles and the power of a point , Gergonne's method uses the conjugate relation between straight lines and their poles in a circle. Methods using circular mirroring were introduced by Julius Peter Christian Petersen in 1879; one example is the ring solution method from HSM Coxeter . The Lie geometry from Sophus Lie provides a further approach .

Algebraic solutions to the Apollonian problem were found in the 17th century by René Descartes and Princess Elisabeth of Bohemia , but they are quite complicated. Practical algebraic methods were developed in the late 18th and 19th centuries by various mathematicians, including Leonhard Euler , Nikolaus Fuss , Carl Friedrich Gauß , Lazare Carnot , and Augustin Louis Cauchy .

If one continues the construction to smaller, touching circles, one is led to Apollonian circle packings, which attracted research interest in the 2000s through connections to homogeneous dynamics and number theory (inter alia Jeffrey Lagarias , Allan Wilks , Peter Sarnak , Alex Kontorovich , Hee Oh ). They are also examples of fractals .

Solution methods

Section of hyperbolas

Figure 3: Two given circles (black) and one circle that touches both (pink). The center-to-center distances, d ₁ and d ₂ , are r ₁ + r _s and r ₂ + r _s , respectively ; therefore their difference is independent of r _s .

Adriaan van Roomen's solution (1596) is based on the intersection of two hyperbolas . The given circles are denoted by C ₁ , C ₂ and C ₃ . Van Roomen solved the general problem by reducing it to a simpler problem, namely, finding circles that touch two given circles, say C ₁ and C ₂ . He found that the center of a circle touching the two given circles must lie on a hyperbola whose focal points are the centers of the given circles. To understand this, the radii of the solution circle and the two given circles should be denoted by r _s , r ₁ and r ₂ , respectively (Figure 3). The distance d ₁ between the centers of the solution circle and from C ₁ is either r _s + r ₁ or r _s - r ₁ - depending on whether these circles are touched in an exclusive or inclusive manner. Correspondingly, the distance d ₂ between the centers of the solution circle and from C _{2 is} either equal to r _s + r ₂ or r _s - r ₂ - again depending on the type of contact. Therefore the difference d ₁ - d _{2 of} these distances is always a constant that is independent of r _s . This property of a fixed difference in the distances between two focal points characterizes hyperbolas; consequently the center of the solution circle must lie on a hyperbola. A second hyperbola can be drawn for the two given circles C ₂ and C ₃ , whereby the type of contact between the solution circle and C ₂ should be consistent with the first hyperbola. The intersection of the two hyperbolas (if not empty) provides the center of the solution circle with the given contact properties. The whole set of solutions to the Apollonian problem can be found by considering all possible combinations of including or excluding touching the three given circles.

Isaac Newton (1687) improved van Roomen's solution by determining the centers of the solution circles by intersecting a straight line and a circle. Newton formulated the Apollonios problem as a problem of trilateration : the determination of a point Z from three given points A , B and C so that the differences in the distances between Z and the three given points have certain values. These four points correspond to the center of the solution circle ( Z ) and the centers of the three given circles ( A , B and C ).

Figure 4: The set of points with a constant ratio of the distances d ₁ / d ₂ to two fixed points is a circle.

Instead of the two hyperbolas, Newton constructs her guidelines . For each hyperbola, the ratio of the distances between a point Z and a focal point A and the guideline is a constant called eccentricity . The two guidelines intersect at a point T , and Newton uses the two known distance ratios to construct a straight line through T on which Z must lie. However, the distance ratio TZ / TA is also known; therefore Z lies on a known circle, since according to Apollonios a circle can be defined as the set of all points whose distances to two given fixed points have a certain ratio ( circle of Apollonios ). (Incidentally, this definition is the basis of the bipolar coordinates .) The problem of Apollonios can therefore be traced back to the intersection of the straight line and the circle.

Viètes reconstruction

As described below, the Apollonian problem has ten special cases that differ in the type of the three given objects, namely circles ( K ), straight lines ( G ) or points ( P ). Usually these ten cases are referred to with abbreviations such as KKP . Viète solved all these cases by constructing with compasses and ruler; he used the solutions of the simpler cases to handle the more complicated cases.

Figure 5: The touch of circles remains when their radii are changed by the same amount. A solution circle (pink) must become larger or smaller with an enclosing touching circle (black circle on the right), while with an exclusionary touch (two black circles on the left) the circles behave in opposite directions

Viète began by solving the PPP case (three points), following Euclid's method as described in the Elements . Building on this, he derived a lemma that corresponds to the theorem about the power of a point , and with its help solved the case of GPP (one line, two points). Also according to Euclid, Viète solved the GGG case (three straight lines) by using bisectors . He then derived a lemma to construct the perpendicular to bisect the angle through a given point, which settled the case of GGP (two straight lines, one point). This solved the first four cases of the Apollonios problem in which no circles were given.

To solve the remaining problems, Viète took advantage of the fact that the given circles and a solution circle can change their size without changing anything about the touch (Figure 5). If the radius of the solution circle is changed by an amount , the radius of the given circles must also change by with an inclusive touch , but with an exclusive touch by . So if the circle of solution swells, the given circles must swell in the same way with inclusive contact and behave in the opposite way with exclusive contact if the touch property is to be retained. ${\ displaystyle \ Delta r}$ ${\ displaystyle \ Delta r}$ ${\ displaystyle - \ Delta r}$

Viète used this approach to shrink one of the given circles to a point; in this way the more complicated cases could be reduced to the simpler, already solved cases. He first solved the KGG case (one circle, two straight lines) by reducing the size of the circle to a point, corresponding to the GGP case . Then he solved the case of KGP (a circle, a straight line, a point) using three lemmas. Again by shrinking a circle to a point, Viète transformed the KKG case into the KGP case . Then he solved the cases KPP (one circle, two points) and KKP (two circles, one point), the second of them with two lemmas. Finally, Viète solved the general case KKK (three circles) by reducing a circle to a point, whereby this sub-problem was reduced to the KKP case .

Algebraic solution

One denotes the centers of the three given circles with

{\ displaystyle M_ {1} = (x_ {1}, y_ {1})}

, and ,

{\ displaystyle M_ {2} = (x_ {2}, y_ {2})}

{\ displaystyle M_ {3} = (x_ {3}, y_ {3})}

whose radii with , and as well as the center and radius of the desired circle with and , then the conditions for the distances of the desired circle center from the given centers lead to an equation system of the following type for the three unknowns , and : ${\ displaystyle r_ {1}}$ ${\ displaystyle r_ {2}}$ ${\ displaystyle r_ {3}}$ ${\ displaystyle M_ {s} = (x_ {s}, y_ {s})}$ ${\ displaystyle r_ {s}}$ ${\ displaystyle x_ {s}}$ ${\ displaystyle y_ {s}}$ ${\ displaystyle r_ {s}}$

{\ displaystyle \ left (x_ {s} -x_ {1} \ right) ^ {2} + \ left (y_ {s} -y_ {1} \ right) ^ {2} = \ left (r_ {s} \ pm r_ {1} \ right) ^ {2}}

{\ displaystyle \ left (x_ {s} -x_ {2} \ right) ^ {2} + \ left (y_ {s} -y_ {2} \ right) ^ {2} = \ left (r_ {s} \ pm r_ {2} \ right) ^ {2}}

{\ displaystyle \ left (x_ {s} -x_ {3} \ right) ^ {2} + \ left (y_ {s} -y_ {3} \ right) ^ {2} = \ left (r_ {s} \ pm r_ {3} \ right) ^ {2}}

The plus sign of applies to the exclusive touch, the minus sign to the inclusive touch. For example, if one subtracts the second equation from the first and the third from the second, one can express and through by solving a linear system of equations with two unknowns. ${\ displaystyle \ pm}$ ${\ displaystyle x_ {s}}$ ${\ displaystyle y_ {s}}$ ${\ displaystyle r_ {s}}$

{\ displaystyle x_ {s} = M + Nr_ {s}}

{\ displaystyle y_ {s} = P + Qr_ {s}}

The coefficients , , and depend on the given circles and the type of contact (one or exclusively) from. ${\ displaystyle M}$ ${\ displaystyle N}$ ${\ displaystyle P}$ ${\ displaystyle Q}$

Plugging these results into one of the given equations gives a quadratic equation that can be used to determine; the coordinates and can then be calculated from this. ${\ displaystyle r_ {s}}$ ${\ displaystyle x_ {s}}$ ${\ displaystyle y_ {s}}$

The procedure described here initially relates to the case of three circles ( KKK ), but can be easily transferred to points if these are understood as circles with a radius of 0. In the case of straight lines, one can set up linear equations for , and from the condition that the center of a solution circle must have the distance ; the rest of the solution is the same as for circles. ${\ displaystyle (x_ {s}, y_ {s})}$ ${\ displaystyle r_ {s}}$ ${\ displaystyle x_ {s}}$ ${\ displaystyle y_ {s}}$ ${\ displaystyle r_ {s}}$

Inversive methods

Figure 6: Inversion on a circle. The point P 'is the mirror point of the point P with respect to the circle.

Inversive geometry forms a natural framework for the problem of Apollonios . The basic strategy of inversive methods is to transform a given Apollonios problem into another Apollonios problem that is easier to solve; the solutions of the original problem are obtained from the solutions of the transformed problem by reversing the transformation. Transformations that transform one Apollonios problem into another come into question; they must therefore transform the given points, circles and straight lines into other points, circles or straight lines, but not into any other forms. The mirroring of a circle has this property and allows you to choose any center and radius of the inversion circle . At first one might think that congruence maps are also possible; however, these would not simplify the problem, but would only result in shifts , rotations and reflections of the original problem.

The inversion on a circle (circular mirroring) with center O and radius R consists of the following operation (Figure 6): each point P is mapped to a new point P ′ , so that O , P and P ′ are collinear and the product of The distances from P and P ′ to the center O are equal to the square of the radius R :

{\ displaystyle {\ overline {\ mathbf {OP}}} \ cdot {\ overline {\ mathbf {OP ^ {\ prime}}}} = R ^ {2}.}

If P lies outside the circle, then P ′ lies inside, and vice versa. If P agrees with O , then one says that the inversion maps P into infinity. (In complex analysis "infinite" is defined on the Riemann sphere .) The inversion has the useful property that lines and circles are always transformed into straight lines or circles, and points always into points. Circles generally merge into circles on inversion; however, if a circle goes through the center of the inversion circle, it is transformed into a straight line, and vice versa. What is significant is the fact that a circle that intersects the inversion circle at right angles is not changed by the inversion, but is mapped onto itself.

The circular reflections correspond to a subset of the Möbius transformations on the Riemann sphere. The plane Apollonios problem can be transferred to the sphere by stereographic projection ; therefore the solutions of the plane problem also apply to the corresponding problem on the sphere. Other inversive solutions to the plane problem are also possible.

Solution pairs regarding inversion

Figure 7: A conjugated pair of solution circles of the Apollonian problem (pink); the given circles are shown in black.

Solutions to the Apollonios problem usually appear in pairs; for every circle of solutions there is a conjugate circle of solutions (Figure 7). One solution circle excludes the given circles that the other solution circle includes, and vice versa. In the example shown, a solution circle (pink, top left) includes two given circles (black), but excludes the third given circle; however, the conjugate solution circle (also pink, bottom right) includes the third given circle, but excludes the other two. The two conjugate solution circles are symmetrical to one another with respect to a mirroring of a circle, as will be explained below.

In general, for any three circles there is a definite radical circle which intersects all three given circles at right angles; the center of this circle is called the radical center . For illustration, the orange drawn circle in Figure 7 intersects the given circles shown in black at right angles. The circle reflection on the radical circle leaves the given circles unchanged, but maps the conjugate solution circles (pink) onto one another. The same mirroring of a circle shows the corresponding contact points of the two solution circles on one another; for clarification, the two blue marked points on each of the green lines are transformed into one another. Therefore, the connecting lines of such conjugate contact points are invariant with respect to the inversion; consequently they must go through the center of the inversion, i.e. through the radical center (green lines that intersect in the orange point of the sketch).

Inversion into a circular ring

If two of the three given circles do not intersect, a center of inversion can be found such that these two circles merge into concentric circles. When using this inversion, the solution circles are mapped to circles within the annulus between the two concentric circles. Therefore they belong to one of two families with one parameter each. In the first family (Figure 8) the solutions do not include the inner of the concentric circles, but lie in the circular ring like the balls of a ball bearing. The second family (Figure 9) includes the interior of the concentric circles. In general, there are four solutions per family, for a total of eight solutions, which is consistent with the algebraic solution .

Figure 8: A solution circle (pink) of the first family lies between two given concentric circles (black). The doubled radius r _{s of} a solution circle corresponds to the difference r _outer - r _inner of the outer and inner radius, while the doubled center-to-center distance d _{s is} equal to the sum of these radii.

Figure 9: A solution circle (pink) of the second family encloses the inner one of the given circles (black). The doubled radius r _{s of} a solution circle corresponds to the sum r _outer + r _inner of the outer and inner radius, while the doubled center-to-center distance d _{s is} equal to the difference between these radii.

If two of the given circles are concentric, the Apollonian problem can easily be solved with a method suggested by Gauss . The radii of the three given circles are known, as is the distance d _non between the center of the concentric circles and the center of the non-concentric circle (Figure 8). A solution circle can be determined from its radius r _s , the angle and the distances d _s and d _T between its center point and the common center point of the concentric circles or the center point of the non-concentric circle. The radius and the distance d _s are known (Figure 8), and for the distance d _T applies d _T = r _s ± r _non - depending on whether the non-concentric circle is touched including or excluding. From the cosine law it now follows ${\ displaystyle \ theta}$

{\ displaystyle \ cos \ theta = {\ frac {d _ {\ mathrm {s}} ^ {2} + d _ {\ mathrm {non}} ^ {2} -d _ {\ mathrm {T}} ^ {2} } {2d _ {\ mathrm {s}} d _ {\ mathrm {non}}}} \ equiv C _ {\ pm}.}

A new constant C was defined here as an abbreviation , the index of which indicates whether the solution circle should be exclusive or inclusive. A simple trigonometric transformation leads to the four solutions

{\ displaystyle \ theta = \ pm 2 \ \ mathrm {atan} \ left ({\ sqrt {\ frac {1-C} {1 + C}}} \ right).}

This formula expresses four solutions because there are two possibilities for and C each. The remaining four solutions are obtained with the same method, using the substitutions for r _s and d _s from Figure 9. All eight solutions to the general Apollonios problem can be found with this method. ${\ displaystyle \ pm}$

Any two disjoint circles can be mapped onto concentric circles as follows. First one constructs the power line of the two given circles; If one chooses any two points P and Q on this straight line, one can construct two circles with the centers P and Q respectively , which intersect the two given circles at right angles. The last two circles constructed intersect at two points. Inversion at one of the two intersection points ( F ) maps the constructed circles onto straight lines that go through F ; the two given circles merge into concentric circles, the third given circle (in general) into a new circle. This follows from the fact that the system of circles is equivalent to a set of Apollonian circles that form a bipolar coordinate system.

Resizing and inversion

The usefulness of the circular mirroring can be increased significantly by changing the size. As already explained in Viète's reconstruction , the radii of the given circles and the solution circle can be changed at the same time, so that the contact property is retained. In this way, the original Apollonios problem can be transformed into another problem that may be easier to solve. For example, four circles can be resized so that one of these circles shrinks to a point; also it is often possible to change two given circles so that they touch each other. Third, circles that intersect can be resized so that they do not intersect; thereafter the inversion into a circular ring can be used. In all of these cases, the solution to the original Apollonios problem is obtained by taking the solution of the transformed problem and reversing the resizing and inversion.

Shrinking a given circle to a point

In the first procedure, the given circles are enlarged or reduced (according to the specifications for touch) until one of these circles shrinks to a point P. In this case the general Apollonios problem ( KKK ) becomes the problem KKP (see case distinction ), i.e. the task of finding a circle that touches the two remaining given circles and goes through the point P. Inversion on a circle with center P transforms the two given circles into new circles and the solution circle into a straight line. Hence the transformed solution corresponds to a straight line that touches the two transformed given circles. There are four such solution lines that can be constructed using the outer and inner similarity centers of the two circles. Another inversion with respect to P and undoing the size changes transform such a straight line into the desired solution circle of the original Apollonios problem. All eight general solutions can be found by zooming in and out according to the specifications for including or excluding touch; however, different given circles may shrink to one point for different solutions.

Resizing two given circles to touch

The second approach changes the radii of the given circles by an amount so that two of the circles touch. The common point of contact serves as the center of the reflection on a circle that intersects each of the two touching circles at two points. Due to the mirroring of the circles, the touching circles are mapped onto two parallel straight lines: because their only common point extends to infinity, the straight lines in the image cannot intersect. The same inversion maps the third circle onto another circle. The solution to the inverted problem must therefore be either (1) a straight line that is parallel to the given parallel straight lines and touches the circle created from the third given circle, or (2) a circle of constant radius that is parallel to the given parallel straight lines and touches the transformed given circle. Another inversion and change of all circle radii around provides a solution circle that touches the three originally given circles. ${\ displaystyle \ Delta r}$ ${\ displaystyle \ Delta r}$

Gergonne's solution

Figure 10: The two tangents (straight lines) in the two contact points of a given circle intersect on the power line R (red) of the two solution circles (pink). The three points of intersection on R are the poles of the straight lines that connect the blue drawn contact points on any given circle (black).

Gergonne's method is based on the fact that pairs of solution circles are considered. Let two solution circles be designated with C _A and C _B (pink circles in Figure 10); the points of contact with the three given circles are A ₁ , A ₂ , A ₃ and B ₁ , B ₂ , B _3, respectively . Gergonne's solution method aims to locate these six points and thus to find the two solution circles.

Gergonne realized that if a line L ₁ can be constructed so that A ₁ and B ₁ must lie on it, then these two points can be determined by intersecting L ₁ with the given circle C ₁ (Figure 10). The other four points of contact can be determined accordingly by finding straight lines L ₂ and L ₃ that go through A ₂ and B ₂ or through A ₃ and B ₃ . In order to construct such a straight line as L ₁ , two points must be identified which lie on this straight line; but these points do not have to be points of contact. Gergonne managed to find two other points for each of these lines. One of these two points has already been mentioned, namely the radical center G , which lies on all three straight lines (Figure 11).

To a respective second point on the straight lines L ₁ , L ₂ and L ₃ to locate Gergonne used a relationship between this straight line and the radical axis R of the solution circles C _A and C _B . To understand this relationship, the two tangents to circle C ₁ at the points of contact with the solution circles ( A ₁ and B ₁ ) should be considered; the intersection of these tangents is the pole of L ₁ with respect to the circle C ₁ . Since the distances between this pole and the contact points A ₁ and B _{1 are the} same, this pole must, by definition, also lie on the power line R of the solution circles (Figure 10). The relationship between pole points and their pole lines is mutual; if the pole of L _{1 is} on R with respect to C ₁ , conversely the pole of R with respect to C _{1 must be} on L ₁ . Hence by constructing R we can find its pole P ₁ with respect to C ₁ ; in this way the required second determination point of L _{1 is obtained} (Figure 11).

Figure 11: The poles (red points) of the power line R in relation to the three given circles (black) lie on the green lines connecting the contact points. These straight lines can be determined from the poles and the radical center (orange).

Gergonne found the power line R of the unknown solution circles as follows. Any pair of circles has two similarity centers; these two points result as the points of intersection of the common tangents of both circles. Hence, for the three given circles there are six similarity centers, two for each pair of circles. Remarkably, these six points lie on four lines, three points on each of the lines; in addition, each of the lines corresponds to the power line of a potential pair of solution circles. To show this, Gergonne considered straight lines through corresponding points of contact on two of the given circles, e.g. B. the connecting straight lines A ₁A ₂ and B ₁B ₂ . Now let X _{3 be} a similarity center for the two circles C ₁ and C ₂ ; then A ₁ , A ₂ and B ₁ , B _{2 are} pairs of antihomologous points, and their connecting lines intersect in X ₃ . It follows that the products of the distances are equal:

{\ displaystyle {\ overline {X_ {3} A_ {1}}} \ cdot {\ overline {X_ {3} A_ {2}}} = {\ overline {X_ {3} B_ {1}}} \ cdot {\ overline {X_ {3} B_ {2}}}}

This shows that X ₃ lies on the power line of the two solution circles. A corresponding argument can be applied to the other two pairs of circles, so that the three similarity centers for the three given circles must lie on the power lines of the pairs of solution circles.

In summary, the straight line L ₁ sought is defined by two points: the radical center G of the three given circles and the pole of one of the four straight lines connecting the similarity centers with respect to C ₁ . Determining the corresponding poles with respect to C ₂ and C ₃ results in the straight lines L ₂ and L ₃ ; in this way all six points can be located, from which a pair of solution circles can be determined. If you repeat this procedure for the other three straight lines connecting similarity centers, you get a further six solution circles, a total of eight solutions. However, if a straight line L _{k has} no intersection with the circle C _k (for the same k ), there is no pair of solution circles for this straight line connecting similarity centers.

Special cases

Case distinction

Table: The ten types of the Apollonios problem
number	Abbreviation	Given	Number of solutions (in general)	Remarks
1	PPP	three points	1	The solution circle is generally the perimeter of the triangle defined by the points. If the 3 points are on a straight line, this straight line is the (improper) solution, or in this case there is no circle as a solution.
2	GPP	a straight line, two points	2	If the straight line that goes through the two points is parallel to the given straight line, then there is only 1 solution.
3	GGP	two straight lines, one point	2	The connecting line from the given point and the intersection of the two straight lines lies in one case inside the solution circle (see picture), in the other case outside (the solution circle is then usually significantly larger).
4th	GGG	three straight lines	4th	the inscribed circle and the 3 circles of the triangle formed from the 3 straight lines
5	KPP	one circle, two points	2	One solution circle lies outside the given circle (see picture), the other surrounds it.
6th	KGP	a circle, a straight line, a point	4th
7th	KKP	two circles, one point	4th	The solution circles either enclose none (see picture), the first, the second or both circles
8th	KGG	one circle, two straight lines	8th
9	KKG	two circles, one straight line	8th
10	KKK	three circles (the classic problem)	8th

The problem can be solved in all cases with the classic means (compass and ruler). If two of the circles have at least one point M in common, the problem can be simplified by reducing it to the case where two of the circles degenerate into straight lines by means of a reflection at a circle with center M.

For the four cases without given circles, solutions for the circle radii can be given with relatively simple possibilities:

Three points

There is generally a solution for three points

There is a solution for three points. If at least two points are on top of each other, there are infinitely many solutions.

The three points form a triangle with sides a , b , c . The circle you are looking for is the circumference of this triangle:

{\ displaystyle r = {\ frac {abc} {4A}} = {\ frac {ab} {2h_ {c}}} = {\ frac {a} {2 \ sin \ alpha}}}

For the determination of the area of A can again Heron's Formula may be used.

One line, two points

There are generally two solutions for a straight line and two points

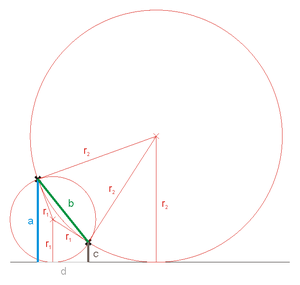
There are two solutions for two points and a straight line, only one for the special cases mentioned below, and no solution for two points on the straight line.

Let the given points be labeled with and , the given straight line with . Next, let the intersection of the straight line with and the angle of intersection . Then, the contact points of the two circles are after have Sekantentangentensatz the distance of . The center points can then be determined as points of intersection of the center perpendiculars from with the perpendiculars to in the contact points. ${\ displaystyle P_ {1}}$ ${\ displaystyle P_ {2}}$ ${\ displaystyle g}$ ${\ displaystyle S}$ ${\ displaystyle (P_ {1} P_ {2})}$ ${\ displaystyle g}$ ${\ displaystyle \ alpha <90 ^ {\ circ}}$ ${\ displaystyle t = {\ sqrt {{\ overline {SP_ {1}}} \ cdot {\ overline {SP_ {2}}}}}}$ ${\ displaystyle S}$ ${\ displaystyle P_ {1} P_ {2}}$ ${\ displaystyle g}$

Two straight lines, one point

There are generally two solutions for two intersecting lines and a point

Construction of the solution for the general case that is close to the straight line intersection

There are different cases:

The straight lines are parallel: If the point lies outside the area bounded by the straight lines, there are no solutions. If it is on one of the straight lines, there is a solution. If it is in between, two solutions; the circle diameter is always equal to the distance between the straight lines.

The straight lines are not parallel:
- If the point does not lie on any of the straight lines, there are two solutions; this is the generic case. Let the image of under the reflection on the associated bisector and the intersection of the perpendicular to through and with the straight . The representation is now symmetrical to the bisector. The distance between the points of contact (of the two circles with ) is obtained with the help of the relationship of the secant-tangent theorem , used with as the center of the straight line . Applied on both sides , the contact points result first . The center points of the circles result from the respective intersection points of the perpendicular to through with the bisector . ${\ displaystyle P '}$ ${\ displaystyle P}$ ${\ displaystyle w}$ ${\ displaystyle S}$ ${\ displaystyle w}$ ${\ displaystyle P}$ ${\ displaystyle P '}$ ${\ displaystyle g}$ ${\ displaystyle B}$ ${\ displaystyle g}$ ${\ displaystyle S}$ ${\ displaystyle S}$ ${\ displaystyle {\ overline {BS}} = {\ sqrt {{\ overline {SP}} \ cdot {\ overline {SP '}}}}}$ ${\ displaystyle g}$ ${\ displaystyle B}$ ${\ displaystyle M}$ ${\ displaystyle g}$ ${\ displaystyle B}$ ${\ displaystyle w}$

Three straight lines

There are four solutions for three intersecting lines

There are four solutions for three intersecting lines (not parallel or on top of each other). If two of the lines are parallel, there are only two solutions, for three parallels there is no solution and for parallel lines with a distance of 0 there are infinitely many solutions.

The three straight lines with their intersection points form a triangle with the sides . Therefore, the rules for the inscribed circle and the approach circles apply here: ${\ displaystyle a, b, c}$

{\ displaystyle r = {\ frac {2A} {a + b + c}} = {\ frac {A} {s}} = {\ frac {a} {\ cot {\ frac {\ beta} {2} } + \ cot {\ frac {\ gamma} {2}}}}}

with the interior angles , the area and half the circumference : ${\ displaystyle \ alpha, \ beta, \ gamma}$ ${\ displaystyle A}$ ${\ displaystyle s}$

{\ displaystyle s = {\ frac {a + b + c} {2}}}

To get an expression that uses only the lengths of the sides, Heron's theorem can be used:

{\ displaystyle A = {\ sqrt {s (sa) (sb) (sc)}}}

The corresponding formulas for the approaches are as follows

{\ displaystyle r_ {a} = {\ frac {2A} {b + ca}} = {\ frac {A} {sa}} = {\ frac {a} {\ tan {\ frac {\ beta} {2 }} + \ tan {\ frac {\ gamma} {2}}}}}

or for the other arrivals accordingly.

Number of solutions

Figure 12: An Apollonios problem without solutions. A solution circle (pink) would have to intersect the dashed circle (black) to touch the other two given circles (also black).

The problem of finding the number of solutions for the various types of Apollonios' problem belongs to the field of enumerative geometry . The general number of solutions to the ten problem variants is given in the table above. However, it happens that special arrangements of the given elements change the number of solutions. For example, the Apollonian problem has no solution if one of the circles separates the other two (Figure 12); to touch the two solid circles, a solution circle would have to intersect the circle shown in broken lines; but that is impossible if the dashed circle is to be touched. Conversely, if the three given circles touch at the same point, then every circle through the common point is a solution; such Apollonios problems have an infinite number of solutions. Also in the case of identical given circles there are in general an infinite number of solutions. If only two circles are identical, there are only two different given circles; the centers of the solution circles form a hyperbola , as shown in the section Intersecting Hyperbolas .

A comprehensive enumeration of the solutions for all possible configurations of three given circles, points or straight lines was first attempted by Muirhead in 1896, although there was earlier work on this by Stoll and Study. Muirhead's investigation, however, was incomplete; it was expanded in 1974. A final count of 33 different cases was published in 1983. Although the solutions to the Apollonian problem usually occur in pairs (see the section on pairs of solutions regarding inversion ), in some cases an odd number of solutions are possible, such as the uniquely determined solution of the problem PPP , or when one of the given circles or all three solutions themselves are. (An example of this are the circles in Descartes' theorem ). However, there is no Apollonios problem with exactly seven solutions.

literature

HSM Coxeter : The problem of Apollonius , American Mathematical Monthly, Volume 75, 1968, pp. 5-15
Frauke Böttcher: The "Apollonian Touch Problem" - A Historical Reconstruction for Teaching Geometric Methods (PDF; 7.2 MB) , University of Cologne, Faculty of Mathematics and Natural Sciences, Seminar for Mathematics and its Didactics ( pdf ).
Dana Mackenzie A tisket, a tasket, an Apollonian basket , American Scientist, Volume 98, 2010, pp. 10-14 (received the 2015 Chauvenet Prize ).

Web links

Commons : Apollonian problem - collection of images, videos and audio files

Individual evidence

↑ ^a ^b ^c ^d ^e A. Bruen, JC Fisher, JB Wilker: Apollonius by inversion . In: Mathematics Magazine . 56, 1983, pp. 97-103
↑ ^a ^b ^c ^d H. Dörrie: The Tangency Problem of Apollonius . In: 100 Great Problems of Elementary Mathematics: Their History and Solutions . 1965, pp. 154-160.
^ ^A ^b Harold Scott MacDonald Coxeter: The Problem of Apollonius . In: The American Mathematical Monthly . Vol. 75, 1968, pp. 5-15.

[Bruen_1983-1] A. Bruen, JC Fisher, JB Wilker: Apollonius by inversion . In: Mathematics Magazine . 56, 1983, pp. 97-103

[Dörrie_1965-2] H. Dörrie: The Tangency Problem of Apollonius . In: 100 Great Problems of Elementary Mathematics: Their History and Solutions . 1965, pp. 154-160.

[Coxeter_1968-3] A ^b Harold Scott MacDonald Coxeter: The Problem of Apollonius . In: The American Mathematical Monthly . Vol. 75, 1968, pp. 5-15.