Tripartite the angle

Under the problem of the trisection of the angle (also: Trisection of the angle ) is understood in the geometry of the question whether an arbitrary angle with the aid of ruler and compass (with the Euclidean tools can be divided) into three equal angle. The tripartite division of the angle is one of the three classic problems of ancient mathematics and can only be carried out for certain angles. Although the problem of the division of angles goes back to antiquity, it was not until the 19th century that algebrabe shown that it can generally not be solved with a compass and ruler. The first proof of this negative statement comes from Pierre Wantzel from the year 1837. In him the problem is reduced to an algebraic equation of the third degree and argues that its solutions are not numbers that can be constructed in a finite number of steps. Since it only needs to be shown that the construction does not generally work, it is sufficient to give a single counterexample. For example, the 20 ° angle cannot be constructed with a compass and ruler, which is why the 60 ° angle cannot be divided into three with these tools.

Although a classic construction is not possible, the trisection of an angle can be carried out precisely with the aid of auxiliary materials such as a marked ruler. Some of these techniques were already known in ancient times. In a striking contrast to the problem of dividing the angle into three parts, there is the very easy way to bisect the angle with a compass and ruler using the bisector .

Classic problem

Examples of angles that can be divided into three:
For the angles 9 ° and 3 °, only the construction of the angle 30 ° and that of the regular pentagon is required .

According to the classic rule, a solution only counts if any given angle is divided into three equal parts with the help of a compass and a non-scaled ruler.

In the case of special angles, it is possible to divide the angle into three, for example with every integer multiple of 3 °.

Even the ancient Greeks tried in vain to find a general solution for any angle. Around 1830, the French mathematician Évariste Galois laid the foundations for later evidence that this is not generally possible. For example, it is not possible to divide the constructible angle 60 ° into thirds, since 20 ° cannot be constructed.

Why this is impossible is explained in the Proof of Impossibility section .

A general three-way division is therefore ultimately only possible if additional aids are used in addition to compasses and rulers - such as a trisectrix - or if markings are made on the ruler. On the other hand, any good approximation solution can be represented with a compass and ruler - as the examples below show.

story

Antiquity

It was the Greeks who in the 5th century BC BC recognized the problem of dividing an arbitrary angle into three equal angles. Presumably this problem came to the fore of mathematical interest when they tried to set up a chordal chart for astronomical purposes . They strove for a solution that could be mastered with compasses and an unmarked ruler - a limitation going back to Oinopides of Chios (~ 440 BC) - but they did not find any that met this requirement. For example, with the tendon table of Ptolemy one encounters the elementary geometrically no longer manageable task of gaining from the tendon for the tendon for . For many centuries until Nicolaus Copernicus (1473–1543) , the trigonometry required for the geometry of the tendons was only understood as a component of astronomy and accordingly dealt with in astronomical works. Regiomontanus wrote the first independent textbook on trigonometry around 1464, but it was only published posthumously, almost 70 years later, in 1533. ${\displaystyle 3^{\circ }}$ ${\displaystyle 1^{\circ }}$

Hippias of Elis (around 460 to 400 BC) was the first to find it around 422 BC. A solution with the help of a so-called additional aid. It was an auxiliary curve, it came to be known as the Trisektrix des Hippias or Quadratrix des Hippias . This is even designed for dividing an angle into equal parts. The name quadratrix comes from the fact that it also answers the problem of circular quadrature . From this it can be concluded that it is a transcendent curve . Nevertheless, it is easy to write on because it is created by two simple movements. ${\displaystyle n}$

Archimedes of Syracuse (287-212 BC) found a pragmatic solution. Although the assignment to Archimedes has not been established, there is a construction of the regular heptagon that has only survived in Arabic. While the regular triangles, squares, pentagons and hexagons can be described in a given circle with a compass and ruler, this is no longer possible with the heptagon. Algebraically, dividing the circle into seven equal parts leads to a cubic equation and therefore belongs to the same problem class as doubling the cube and dividing the angles into three. The construction allegedly found by Archimedes only works with these two devices, but uses the ruler in a way that is not permitted in Euclidean geometry: It is rotated around a fixed point until two triangles, one of which grows as the rotation increases , while the other is decreasing, are equal in area. This is a special type of slide-in construction or so-called Neusis. Although the method used is of theoretical interest, it cannot be used in practice. Today it is called the Neusis construction . Archimedes later created a special curve, called it spiral ( Archimedean spiral ) and used it to study the angular division and the squaring of the circle.

In the 2nd century BC BC Nicomedes invented an instrument that made it possible to mechanically meet the demands of the Neusis construction handed down by Pappos. The curves that can be constructed with this were given the name conchoid , in German shell curves, because of their shape . The instrument consists of two T-shaped rulers firmly connected to one another, on which a third one can move in a certain way. It thus served as an additional aid for dividing the angle into three.

Pappos of Alexandria (4th century AD) belonged to the circle of the Alexandrian Neoplatonists . His collections are a compilation of eight books; except for the first and the beginning of the second, they have all been preserved. In the early modern period, European mathematicians took many suggestions from the Collectiones , as they contain important excerpts from the writings of Euclid , Apollonios , Archimedes and other mathematicians. Pappos expanded these excerpts with critical comments and some of his own additions. He showed, inter alia. two different variants for solving the angular trisection with aids - a pragmatic one with a marked ruler as an additional aid, i.e. a Neusis construction (see the section The Pappos method ) and a second in which he used the hyperbola as a trisectrix .

Early to late Middle Ages

Ahmad ibn Mūsā lived in Baghdad in the middle of the 9th century and was one of the three brothers who called themselves Banū Mūsā . He was an astronomer and a mathematician. His solution shows two predetermined asymptotes of a hyperbola passing through a given point. A marked ruler and thus a Neusis construction is required to divide the angle into thirds. His solution was very similar to that of Pappos' paper strip construction (see the section The Pappos Method ).

Thabit ibn Qurra (826–901) from Baghdad was initially a money changer, took an interest in science, was trained in mathematics and also studied philosophy and astronomy. He also used the hyperbola for his Neusis construction. However, in contrast to that of Ahmad ibn Mûsâ, its construction was described more precisely and explained in more detail. His solution was also very similar to Pappo's paper strip construction.

Muslim astronomy and trigonometry reached their peak in the 15th century at the Ulug Beg observatory in Samarkand . There was al-Kashi active, which a skilled iteration availed to with great accuracy from the angle tripartite equation of the sine calculate. In principle, he proceeded as follows. Since it could be determined as precisely as required (e.g. it could be constructed from the difference between the pentagon and the hexagon with a pair of compasses and ruler), he used the equation of three-division angles ${\displaystyle 1^{\circ }}$ ${\displaystyle \sin(3^{\circ })}$ ${\displaystyle 36^{\circ }}$ ${\displaystyle 30^{\circ }}$

${\displaystyle \sin(3\alpha )=3\sin(\alpha )-4\sin(\alpha )^{3}}$.

It was first found in this trigonometric notation at the end of the 16th century in Vieta . She is the type (in the former classification were coefficients - here , - assumed to be positive). Al-Kashi computed the first approximation from to . The second approximation then follows analogously from etc., whereby a special feature is that a further sexagesimal point can be exactly determined with each step . The result of al-Kashi, converted into decimal notation, provides 18 digits: ${\displaystyle x^{3}+q=px}$ ${\displaystyle p={\tfrac {3}{4}}}$ ${\displaystyle q={\tfrac {1}{4}}\sin(3^{\circ })}$ ${\displaystyle x={\tfrac {q+x^{3}}{p}}\approx {\tfrac {q}{p}}}$ ${\displaystyle x_{1}={\tfrac {q}{p}}}$ ${\displaystyle x_{2}={\tfrac {q+x_{1}^{3}}{p}}}$

${\displaystyle \sin(1^{\circ })=0{,}\,017\,452\,406\,437\,283\,571\,\dots }$

A large number of Arabic manuscripts are still unseen in oriental libraries, so that research has not yet been able to work out a complete picture of the development and the knowledge achieved.

Renaissance to modern times

As a mathematician, Albrecht Dürer also contributed to the theory of the three-dimensional division of angles. In addition to good approximation constructions for the regular 7-, 9-, 11- and 13-gon, the second book of his Underweysung also contains the approximate three-way division. In 1931 it was compared with several other approximate solutions for the same problem and it was shown that it nowhere deviates from the exact value by more than about 20 arc seconds and thus surpasses all other suggested solutions. Dürer's design idea can also be iterated easily and, after a few steps, delivers a very high level of accuracy. In everything, Dürer is always aware of the fundamental difference between exact, he calls them demonstrative , and approximate solutions, he calls them mechanice , and thus stands out even from most of the professional mathematicians of his time.

The first person to prove that the problem was unsolvable - using only a pair of compasses and ruler - was Pierre-Laurent Wantzel in 1837. However, historians doubt that Wantzel was the first to know of proof , as the young Carl did Friedrich Gauss very likely had one. A large part of his work Disquisitiones arithmeticae , published in 1801, is devoted to the question of which conditions a polynomial equation must meet in order to be solvable by quadratic radicals. There you will also find the sentences named after Gauss, with the help of which the unsolvability of most classical tasks can be demonstrated with a compass and ruler. With the techniques he developed, Gauss proved, for example, that the 17-sided can be constructed with a compass and ruler. The math historians Christoph Scriba and Peter Schreiber attribute the fact that, despite this, Wantzel is named and quoted by many authors as the originator of the sentences to the “communication difficulties” of 19th century science .

Proof of impossibility

History of evidence

It is generally not possible to divide the angle into three parts with a compass and ruler alone

Pierre Wantzel published a proof in 1837 that it is generally impossible to divide a square into three equal parts with a compass and ruler. His proof uses, if one puts it in modern terminology, field extensions as treated in abstract algebra and in particular in Galois theory . Wantzel published these results earlier than Galois (whose work came out in 1846) and did not need the connection between body extensions and groups that Galois theory deals with. His proof was based on the following algebraic considerations:

1. In the first part of the proof, he argues that if a design problem can be solved with a ruler and compass, “the unknown of the problem can be obtained by solving a series of quadratic equations whose coefficients are rational functions of the parameters of the problem and the The roots of the previous equations are ”. ${\displaystyle p,q,r,\dots }$

The "unknown of the problem" means, for example, the route you are looking for . ${\displaystyle x=\cos(\alpha )}$

2. He then showed that every algebraic number is the solution of the last equation of a system ${\displaystyle x_{n}^{0}}$ ${\displaystyle x_{n}^{2}+A_{n-1}x_{n}+B_{n-1}=0}$

${\displaystyle {\begin{aligned}&x_{1}^{2}+Ax_{1}+B=0\\&x_{2}^{2}+A_{1}x_{2}+B_{1}=0\\&\vdots \\&x_{n}^{2}+A_{n-1}x_{n}+B_{n-1}=0\end{aligned}}}$

is, where the coefficients are always in the body by successive adjunction , solves a polynomial equation of degree with coefficients in . Doing so solves the equation and are the given parameters of the problem. ${\displaystyle A_{m},B_{m}}$ ${\displaystyle \mathbb {Q} (p,q,r,\dots ,x_{1}^{0},\dots ,x_{m}^{0})}$ ${\displaystyle 2^{n}}$ ${\displaystyle \mathbb {Q} (p,q,r,\dots )}$ ${\displaystyle x_{j}^{0}}$ ${\displaystyle x_{j}^{2}+A_{j-1}x_{j}+B_{j-1}=0}$ ${\displaystyle p,q,r,\dots }$

3. Wantzel knew that every algebraic number is the zero of a polynomial with a power of two, if this is chosen to be sufficiently large. Hence, its main result was to show that if the number of equations required were reduced to a minimum, the resulting polynomial is irreducible over . ${\displaystyle \mathbb {Q} (p,q,r,\dots )}$

The impossibility of the construction now follows as a corollary from sentences 1 to 3: If, starting with the segments 0, 1 and , it were possible to divide an angle into three with a compass and ruler, then the zero of an irreducible polynomial would have to be above , the degree would have to be a power of two Has. The polynomial is generally irreducible over , but has degree 3. This is a contradiction. ${\displaystyle \cos(3\alpha )}$ ${\displaystyle 3\alpha }$ ${\displaystyle \cos(\alpha )}$ ${\displaystyle \mathbb {Q} (\cos(3\alpha ))}$ ${\displaystyle 4x^{3}-3x-\cos(3\alpha )}$ ${\displaystyle \mathbb {Q} (\cos(3\alpha ))}$

It should be noted that Wantzel's original publication is viewed by the mathematician Jesper Lützen as incomplete and difficult to understand - this applies above all to the “proof” of main proposition 3. Lützen closed the gaps afterwards and the results as described above , formulated in modern technical language. Wantzel's proof of the impossibility of constructing the trisection of the angle and the doubling of the cube with a ruler and compass was forgotten for almost a century after its publication in 1837. According to Lützen, the “lack of notoriety of the author”, the “fact that some of his contemporaries regarded the result as known or even proven”, and that “the result was not regarded as an important mathematical result at the time of its publication” driving reasons.

Algebraic proof

Are known , or , the angle can be constructed. So the question is whether, for example , one can construct the number from the information with a compass and ruler . ${\displaystyle \cos(\theta )}$ ${\displaystyle \sin(\theta )}$ ${\displaystyle e^{i\theta }}$ ${\displaystyle \theta }$ ${\displaystyle e^{3i\theta }}$ ${\displaystyle e^{i\theta }}$

The angle is divided into three by means of the third unit roots in the complex number plane ${\displaystyle 360^{\circ }}$

The problem of constructing an angle of given size is equivalent to constructing two lines whose lengths are related . The solution of one of these two problems with a compass and ruler results in the solution of the other. Using the triple angle cosine formula ${\displaystyle \alpha }$ ${\displaystyle \cos(\alpha )}$

${\displaystyle \cos(3\alpha )=4\cos ^{3}(\alpha )-3\cos(\alpha )}$

an algebraic equation can be set up that connects the values and . It follows that the problem of angular trisection is equivalent to constructing a particular line segment where the ratio of line length to unit length equals a solution to a particular cubic equation . The original geometric problem is thus reduced to a purely algebraic problem. ${\displaystyle \cos(3\alpha )}$ ${\displaystyle \cos(\alpha )}$

The cubic equation can easily be deduced from De Moivre's formula for the complex exponential function . According to Euler's formula, the following applies

${\displaystyle e^{i\alpha }=\cos(\alpha )+i\sin(\alpha )}$

and by raising both sides to the power of 3, the equation can be read off by comparing the real parts and. It denotes the imaginary unit of the complex numbers. ${\displaystyle (e^{i\alpha })^{3}=e^{3i\alpha }}$ ${\displaystyle i}$

The proof of the impossibility of the three-dimensional division of the angles can be carried out in detail using the following ideas from algebra . Let there be a set of points ( complex numbers ) containing at least 0 and 1 and an arbitrary point . For these considerations, it is important that the complex numbers can be understood as a plane - in contrast to this, the real numbers are simply understood as a straight line. Then it applies that the point can be constructed from the points with a compass and ruler if and only if it lies in a body (here is the body of the complex numbers), which is created by the adjunct of a square root from the body ${\displaystyle M}$ ${\displaystyle z}$ ${\displaystyle z}$ ${\displaystyle M}$ ${\displaystyle E\subset \mathbb {C} }$ ${\displaystyle \mathbb {C} }$

${\displaystyle K:=\mathbb {Q} (M\cup {\overline {M}})\subset \mathbb {C} }$

emerges. Roughly speaking, this is the amount that is created by forming all sums, differences, products and quotients from rational numbers . Here is the set of the complex conjugates of all elements of and the symbol stands for the union of two sets. Adjunction of a square root means that there must be a such that . For example, the adjunction of a square root of the rational numbers shows that is a rational number - correspondingly is the set of all sums, differences, products and quotients of rational numbers with the number . When there is a so-called field extension . The problem of dividing the angle into three with a pair of compasses and ruler can be reduced to the question of whether the number lies in a partial field of , which can be obtained from successive adjunction of square roots. However, this means that the expansion degree of from a power of 2 must be. But it is in general ${\displaystyle \mathbb {Q} (M\cup {\overline {M}})}$ ${\displaystyle M\cup {\overline {M}}}$ ${\displaystyle {\overline {M}}=\{{\overline {m}}\mid m\in M\}}$ ${\displaystyle M}$ ${\displaystyle \cup }$ ${\displaystyle w^{2}\in K}$ ${\displaystyle E=K(w)}$ ${\displaystyle \mathbb {Q} ({\sqrt {2}})}$ ${\displaystyle ({\sqrt {2}})^{2}=2}$ ${\displaystyle \mathbb {Q} ({\sqrt {2}})}$ ${\displaystyle {\sqrt {2}}}$ ${\displaystyle E\mid K}$ ${\displaystyle \cos(\alpha )}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {Q} (\cos(3\alpha ))}$ ${\displaystyle E}$ ${\displaystyle \mathbb {Q} }$

${\displaystyle [\mathbb {Q} (\cos(\alpha ),\cos(3\alpha )):\mathbb {Q} (\cos(3\alpha ))]=3\not =2^{n}\qquad {\text{für alle}}\,n\in \mathbb {N} ,}$

which makes it impossible to divide the angle into three with a compass and ruler. That the field extension generally grade 3, it can be seen as follows: If the polynomial for reducible over the rational numbers, it would have a rational root. Due to can be studied equivalently . After the rational root theorem only the values are , , and as rational zeros of this equation in question. All of these values ​​can be excluded by substituting them as zeros. Thus over must be irreducible , and the minimal polynomial of over has degree 3. ${\displaystyle \mathbb {Q} (\cos(\alpha ),\cos(3\alpha ))\mid \mathbb {Q} (\cos(3\alpha ))}$ ${\displaystyle p(x)=4x^{3}-3x-\cos(3\alpha )}$ ${\displaystyle 3\alpha ={\tfrac {\pi }{3}}}$ ${\displaystyle \cos({\tfrac {\pi }{3}})={\tfrac {1}{2}}}$ ${\displaystyle 8x^{3}-6x-1=0}$ ${\displaystyle \pm 1}$ ${\displaystyle \pm {\tfrac {1}{2}}}$ ${\displaystyle \pm {\tfrac {1}{4}}}$ ${\displaystyle \pm {\tfrac {1}{8}}}$ ${\displaystyle p(x)}$ ${\displaystyle \mathbb {Q} (\cos({\tfrac {\pi }{3}}))=\mathbb {Q} ({\tfrac {1}{2}})=\mathbb {Q} }$ ${\displaystyle \cos({\tfrac {\pi }{9}})}$ ${\displaystyle \mathbb {Q} }$

It can be shown that the angle cannot be divided into three with a compass and ruler if is a transcendent number . ${\displaystyle \vartheta }$ ${\displaystyle e^{i\vartheta }}$

generalization

A generalization of the problem is to characterize exactly which angles can be constructed and which cannot. Equivalent problems are, for which natural numbers to a circuit in can be divided pieces of equal size by means of ruler and compass or which regular polygons constructible are. The exact characterization of the constructible corner was achieved in 1837 by Pierre Wantzel (after substantial preparatory work by Carl Friedrich Gauß and Évariste Galois ) and states that this is the case exactly when a product of a power of two and pairwise different Fermat's prime numbers is. An angle can be divided into equal angles if and only if the product of a power of two and pairs of different Fermatian prime numbers that do not divide. In particular, it follows that it can be classically divided into thirds if and only if it is not divisible by 3, since 3 is a Fermat prime number. For example, the angle (that is ) can be divided into thirds, since and 3 does not divide the 8. On the other hand, in the case of the angle (that is ) it cannot be divided into three with a compass and ruler, since the number 15 is divisible by 3. ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle {\tfrac {2\pi }{N}}}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle N}$ ${\displaystyle {\tfrac {2\pi }{N}}}$ ${\displaystyle N}$ ${\displaystyle {\tfrac {\pi }{4}}}$ ${\displaystyle 45^{\circ }}$ ${\displaystyle {\tfrac {\pi }{4}}={\tfrac {2\pi }{8}}}$ ${\displaystyle N=15}$ ${\displaystyle {\tfrac {2\pi }{15}}}$ ${\displaystyle 24^{\circ }}$

The first decisive step beyond the mathematics of antiquity was thanks to the young Gauss with his discovery that the regular seventeen-sided can be constructed.

The only known Fermat prime numbers are 3, 5, 17, 257, and 65537. In general, Fermat numbers are the numbers , themselves being a power of two. It is believed that all Fermat numbers are compound numbers . ${\displaystyle 2^{m}+1}$ ${\displaystyle m=2^{q}}$ ${\displaystyle q>4}$

The advanced theories of Gauss and Galois are not needed for the problem of the three-dimensional division of angles. Here it is sufficient to recognize that a route length which satisfies an irreducible equation of the third degree cannot be constructed; because every constructible route length can be obtained algebraically by solving quadratic equations one after the other, so it is algebraically of a power of two.

Attempts at solutions by amateurs

So although the impossibility of dividing the angle into three parts with compasses and ruler has been known for a long time, amateurs inundated mathematical journals and faculties with attempts to prove it. Underwood Dudley , who analyzed the phenomenon, describes the typical trisector as an older man who heard about the problem in his youth (it is probably the most accessible of the three classic problems to the layman) and tinkered with it in retirement. Dudley, who collected hundreds of her attempts at evidence, found only two women among the three-cornered dividers .

Another characteristic, said Dudley, is that laypeople do not understand the meaning of “impossible” in mathematics and instead see it as a challenge. Typically, they have little knowledge of mathematics, but that doesn't necessarily mean that the errors in their designs are easy to find. Characteristically, their diagrams are very complex, but can often be drastically simplified with geometric knowledge. Furthermore, they are convinced of the importance of their solutions for technical applications, which in turn is not unimportant for many patent and confidentiality issues.

After trying many methods of dealing with stubborn angled three-parters, Dudley recommended praising their work as a contribution to a better approximation of the problem (either for its simplicity or its elegance). In addition, you should send them a computer printout showing the error of the experiment for different angles, as well as examples of “approximate solutions” of other angle three-divisors.

Non-classical procedures

If you do not limit yourself to the classic construction rules for compasses and rulers, but also allow the use of other construction tools and mathematical auxiliary objects, or if you are content with approximate solutions, there are a multitude of possible methods of dividing any angle into three. Some of them are presented as examples in the following sections.

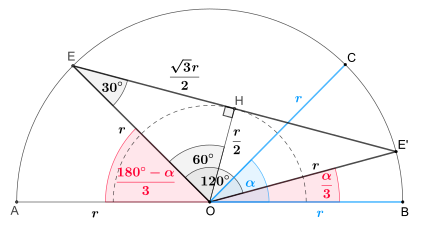
Archimedes' method

Required creation process of the construction

Archimedes was a pragmatist, he gave a solution in his Liber Assumptorum . Let it be the angle to be divided into three as shown in the adjacent drawing. Then proceed as follows: ${\displaystyle \alpha }$

1. Wrap a semicircle with any radius . ${\displaystyle A}$ ${\displaystyle r}$
2. Make two marks on the ruler at a distance . ${\displaystyle r}$
3. Place the ruler so that one of the two markings is on the straight line in the point and the other on the circular line in the point , and draw the line . ${\displaystyle B}$ ${\displaystyle AD}$ ${\displaystyle D}$ ${\displaystyle C}$ ${\displaystyle {\overline {BD}}}$
4. The angle at is the third angle you are looking for. ${\displaystyle \beta }$ ${\displaystyle D}$

Evidence for the three-dimensional division of angles according to Archimedes: ${\displaystyle \alpha =3\beta }$

Laying out the ruler for angle widths is parallel to ${\displaystyle 135^{\circ }<\alpha <270^{\circ },}$
${\displaystyle {\overline {AF}}}$ ${\displaystyle {\overline {DC}}}$

Laying out the ruler for is parallel to ${\displaystyle \alpha >270^{\circ },}$
${\displaystyle {\overline {AF}}}$ ${\displaystyle {\overline {DC}}}$

As a justification, note that because of the special positioning of the ruler, the length of the line is equal to the distance between the markings, i.e. equal to the radius of the circle, which can also be found as and . In particular, the triangle is isosceles, which is why the angle also occurs at. The angle of the triangle at is on the one hand the same (angle sum in the triangle), on the other hand the secondary angle of , is . Since the triangle is also isosceles, the angle also appears at, and the angle of this triangle at is equal . If we consider now, the angle at that to add concerns . ${\displaystyle {\overline {CD}}}$ ${\displaystyle r}$ ${\displaystyle {\overline {AC}}}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle ACD}$ ${\displaystyle \beta }$ ${\displaystyle A}$ ${\displaystyle ACD}$ ${\displaystyle C}$ ${\displaystyle 180^{\circ }-2\beta }$ ${\displaystyle \gamma }$ ${\displaystyle \gamma =2\beta }$ ${\displaystyle ABC}$ ${\displaystyle \gamma }$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle 180^{\circ }-2\gamma }$ ${\displaystyle A}$ ${\displaystyle 180^{\circ }}$ ${\displaystyle \alpha =180^{\circ }-(180^{\circ }-2\gamma )-\beta =2\gamma -\beta =4\beta -\beta =3\beta }$

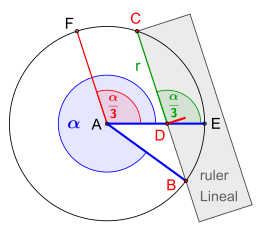
The fact that with this method every angle can be divided into three parts, as has been proven, does not contradict the insolubility of the classic problem, because the above construction was not carried out according to the classically required rules. A mark on the ruler and a clever application of the ruler do not correspond to classic construction methods. A different set of instruments was used and the possible constructions depend on the set of instruments.

The method of the pappos

Method of the Pappos, Neusis construction

The Neusis construction of the Pappos for the trisection of acute angles, described below, dates from late antiquity .

The angle is to be divided , see the illustration on the right: ${\displaystyle \angle {BAD}=3\alpha }$

After drawing the two angled legs and , any length can be determined as the line on the leg . A parallel to ab as well as the perpendicular ab with the base point on follow. Now, the ruler, on which the length is equal to is selected, moved, until the vertex at the parallels is, the length of the track in cuts and thereby the edge of the ruler through the apex extends. The angle found in this way is the angle you are looking for ${\displaystyle {\overline {AB}}}$ ${\displaystyle {\overline {AD}}}$ ${\displaystyle a}$ ${\displaystyle {\overline {AC}}}$ ${\displaystyle {\overline {AD}}}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle E}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle 2a}$ ${\displaystyle G}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle 2a}$ ${\displaystyle {\overline {CE}}}$ ${\displaystyle F}$ ${\displaystyle A}$ ${\displaystyle \angle {BAG}}$ ${\displaystyle \alpha .}$

Because this angle is as alternate angles equal to the peripheral angle of the chord and after the circle angle set is the associated central angle equal Because the triangle is isosceles, also applies This angle but is equal to the difference so true and it follows ${\displaystyle \angle BAG=:\beta }$ ${\displaystyle \angle AGC=\angle FGC,}$ ${\displaystyle {\overline {CF}},}$ ${\displaystyle \angle FMC}$ ${\displaystyle 2\beta .}$ ${\displaystyle \triangle AMC}$ ${\displaystyle \angle FAC=2\beta .}$ ${\displaystyle \angle BAD-\angle BAG=3\alpha -\beta ,}$ ${\displaystyle 2\beta =3\alpha -\beta }$ ${\displaystyle \beta =\alpha .}$

The dashed lines and the center point are not required for the construction, they are only used as evidence. ${\displaystyle M}$

Split with Tomahawk

The tomahawk is a figure which, from a mathematical point of view, consists of two perpendicular lines and a semicircle adjacent to one of the straight lines; the rear end is as long as the radius of the semicircle (see drawing). The name tomahawk comes from the fact that the figure vaguely resembles a tomahawk (an Indian battle ax). To divide an angle into three parts using the tomahawk, you have to position it (see Figure 1) so that its "stem" (handle of the tomahawk) goes through the apex, while the semicircle (the blade of the tomahawk) and the "hook" ( the rear tip of the tomahawk) touch the legs of the angle. In this position, the handle forms an angle with one of the legs which is exactly one third of the starting angle. The connection of the center of the semicircle with the angle tip divides the second and third third of the starting angle. Since the tomahawk is a figure that has to be created, this method does not conform to the classic construction rules (ruler and compass).

If it is not possible to divide an angle directly into three with the help of a tomahawk (see Figure 3) because the given angle is too small to be able to position the tomahawk, the three-way division of the small angle can be constructed from the three-part division of the associated large secondary angle . If you look at an angle with its secondary angle on a semicircle with a radius , you get a constant angle that does not depend on the size of the angle (see drawing). This angle is part of an isosceles triangle, the height of which is. This then results in the construction described in the next paragraph. ${\displaystyle \alpha }$ ${\displaystyle r}$ ${\displaystyle {\tfrac {2}{3}}(180^{\circ }-\alpha )+{\tfrac {2}{3}}\alpha =120^{\circ }}$ ${\displaystyle \alpha }$ ${\displaystyle 120^{\circ }}$ ${\displaystyle {\tfrac {r}{2}}}$

• 

  Figure 1
  Trisection of an angle with a tomahawk. The triangles of the same size are highlighted in red / yellow / green.

• 

  Figure 2
  Template (schematic representation) for three-way division of angles from 90 ° (red) to 180 ° (blue)

• 

  Fig. 3
  Isosceles triangle with height ${\displaystyle \triangle EOE^{\prime }}$ ${\displaystyle |OH|={\tfrac {r}{2}}}$

• 

  Figure 4
  Position of the tomahawk (light blue) for small angles

It begins (see Fig. 4) with drawing in the diameter , halving it in and drawing the semicircle over it . This is followed by entering the given angle with its two angled legs. Now, the Tomahawk is positioned as follows: the "hook" is located on the track of the half-circle touches the upper angle leg and the "stem" passes through the center with the plotting of the two paths , and obtains the three-division of the supplement angle . In order to achieve a three-way division of the angle , the point is now mirrored onto the circular arc . For this purpose, the radius is in half and a semi-circle around from drawn, this results in the point of intersection . Finally, you need a semicircle with a radius , the intersection point and the straight line from through to the arc . The intersection point created in this way is a reflection of the point on the virtual route . Thus the constructed angle is exactly one third of the given angle . ${\displaystyle {\overline {AB}}}$ ${\displaystyle O}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle \angle BOC}$ ${\displaystyle {\overline {AO}},}$ ${\displaystyle O.}$ ${\displaystyle {\overline {DO}}}$ ${\displaystyle {\overline {EO}}}$ ${\displaystyle \angle {COA}}$ ${\displaystyle \angle BOC}$ ${\displaystyle E}$ ${\displaystyle OBC}$ ${\displaystyle {\overline {AO}}}$ ${\displaystyle F}$ ${\displaystyle O}$ ${\displaystyle F}$ ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle {\overline {GO}}}$ ${\displaystyle H}$ ${\displaystyle E}$ ${\displaystyle H}$ ${\displaystyle OBC}$ ${\displaystyle E'}$ ${\displaystyle E}$ ${\displaystyle {\overline {HO}}}$ ${\displaystyle \angle {BOE'}}$ ${\displaystyle \angle {BOC}}$

Division with a right-angled triangular ruler

The angle is divided into three by means of the right-angled hook according to Ludwig Bieberbach, animation, at the end of a 60-second break

In 1932 Ludwig Bieberbach published his work on the teaching of cubic constructions. In it he explains:

“In the following it will be shown that all cubic constructions can be solved if, in addition to the usual use of compasses and rulers, the following use of the right-angled hook is permitted: It is to be placed in such a way that one leg goes through a given point and the other leg touches a given circle, but its vertex lies on a given straight line, where it marks the point to be newly constructed. "

- Ludwig Bieberbach : Journal for pure and applied mathematics , DigiZeitschriften

The angle should be divided into three. If you set ${\displaystyle \delta }$

${\displaystyle \alpha =\cos(\delta )}$  and   ${\displaystyle z=\cos \left({\frac {\delta }{3}}\right),}$

this leads to the equation

${\displaystyle z^{3}-{\frac {3}{4}}z-{\frac {\alpha }{4}}=0.}$

The following description of the animated construction on the left - based on that of von Bieberbach - contains its continuation up to the complete trisection of the angle.

It begins with the first unit circle (basis for Bieberbach's argumentation, in principle a circle with any radius is also expedient) around its center point , the first angle leg and the subsequent second unit circle around . Now the diameter is extended from to the circular line of the second unit circle, which results in the point of intersection . This is followed by the arc around with the radius and the drawing in of the second angle leg of the third angle , which results in the point . ${\displaystyle A}$ ${\displaystyle {\overline {BP}}}$ ${\displaystyle P}$ ${\displaystyle {\overline {BP}}}$ ${\displaystyle P}$ ${\displaystyle O}$ ${\displaystyle P}$ ${\displaystyle {\overline {PB}}}$ ${\displaystyle \delta }$ ${\displaystyle C}$

Now the so-called additional construction means are used, in the example shown it is the set square . This is now placed on the drawing in the following way: The vertex of the angle determines the point on the angle leg , one leg of the triangle runs through the point and the other tangent to the unit circle . After connecting the point with and drawing the tangent from to the unit circle around , the above-mentioned right - angled hook appears . The angle included by the lines and is therefore exact . It continues with the parallels from , besides, the resulting change angle or Z-angle and the point on the circular arc around . Another parallel to ab redefines the point of contact between the tangent and the unit circle . Finally, draw a straight line through until it cuts the arc of the circle in . ${\displaystyle 90^{\circ }}$ ${\displaystyle {\overline {PC}}}$ ${\displaystyle S}$ ${\displaystyle O}$ ${\displaystyle A}$ ${\displaystyle O}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle A}$ ${\displaystyle {\overline {OS}}}$ ${\displaystyle {\overline {PS}}}$ ${\displaystyle {\tfrac {\delta }{3}}}$ ${\displaystyle {\overline {OS}}}$ ${\displaystyle P}$ ${\displaystyle {\tfrac {\delta }{3}}}$ ${\displaystyle D}$ ${\displaystyle P}$ ${\displaystyle {\overline {OS}}}$ ${\displaystyle A}$ ${\displaystyle E}$ ${\displaystyle A}$ ${\displaystyle P}$ ${\displaystyle E}$ ${\displaystyle P}$ ${\displaystyle F}$

So the angle is because of ${\displaystyle \delta }$

${\displaystyle {\overline {PS}}=2\cdot \cos \left({\frac {\delta }{3}}\right)}$

exactly divided into thirds.

Curves

→ Main article : Trisektrix

Three-way division of the angle with the help of the Trisektrix des Hippias, the third section provides the curve section of the Trisektrix (red) ${\displaystyle {\overline {AO}}}$ ${\displaystyle {\overline {TU}}}$

A curve is called TrisTRRIX , which enables the exact third of an angle with a compass and ruler. The existence or constructibility of the curve with other means than compasses and rulers is given here and with the aid of this curve as the only additional aid it is then possible to divide an angle into thirds. In contrast to pure construction with compasses and ruler, points can not only be constructed by intersecting straight lines and circles, but also by intersecting straight lines and circles with the given curve. The entirety of the curve points themselves cannot be constructed with compasses and rulers, which is why the use of such a curve is a violation of the classic rules for angle trisection.

Tripartite different angles with the help of a single hyperbola

Three-way division of the angle with the help of a single hyperbola
hyperbola equation the circular tendon (green) is constant ${\displaystyle y^{2}=3x^{2}-2sx,}$
${\displaystyle {\overline {S_{2}F_{1}}}}$

→ Main article: Hyperbola, Hyperbola as Trisektrix

In 1902 K. Matter published the essay on the trisection of the angle . In it he shows a method that makes it possible to divide different angles into thirds with just one hyperbola.

"A neat and simple geometric solution to our problem of the three-dimensional division of the angle, which differs somewhat from the [...] general method, is the following, in which the construction of a single hyperbola in connection with a circle is necessary."

- K. Matter : ZOBODAT

Selection of the most famous trisectrices

• Trisffektix of Hippias (5th century BC) as well as the
• Archimedes' spirals (3rd century BC) are among the oldest examples of such curves.
• Hyperbola as Trisektrix , this curve was used by Pappos in the 4th century AD to solve this problem.
• Parabola as Trisektrix , described by René Descartes in his work La Geometria from 1637.
• Pascal snail as Trisektrix , found by the French lawyer Étienne Pascal around 1637.
• Cycloid of Ceva , discovered by the Italian Jesuit Tommaso Ceva (1648–1736), also makes it possible to divide any angle into thirds.
• Maclaurin-Trisektrix , was studied by Colin Maclaurinn in 1742.
• Trisektrix von Longchamps , comes from the French mathematician Gohierre de Longchamps (1842–1906).

Dividing the angle into three with origami

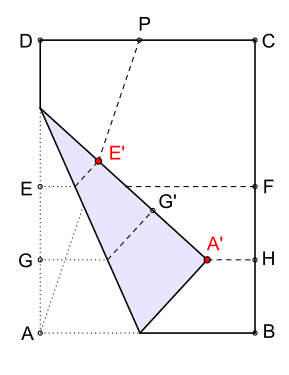
While the three-dimensional division of the angle is not possible with the classical instruments of geometry, the task can be solved with the paper-folding technique origami . A rectangular or square sheet of paper is used for this. It takes six folds of the sheet to divide an angle into three . ${\displaystyle 0^{\circ }<3\alpha <90^{\circ }}$

First the sheet is folded in the middle (see picture 1), this results in the points on the two sheet edges and alternatively, the length of the distance can also be specified with a freely selectable length . The fold follows, it halves the distance point is now determined at will (see image 2) on the distance and then the sheet is folded from to . This results in the angle at the apex ${\displaystyle E}$ ${\displaystyle F.}$ ${\displaystyle {\overline {EF}}}$ ${\displaystyle {\overline {AE}}}$ ${\displaystyle {\overline {GH}},}$ ${\displaystyle {\overline {AE}}.}$ ${\displaystyle P}$ ${\displaystyle {\overline {CD}}}$ ${\displaystyle A}$ ${\displaystyle P}$ ${\displaystyle 3\alpha }$ ${\displaystyle A.}$

Now the decisive fourth fold follows (see image 3) to divide the angle into three , by first placing the corner on the fold and the point on the fold . After marking the point on the sheet, the corner is bent back and the point of intersection is marked - created by the fourth fold with - the sheet has its rectangular shape again. ${\displaystyle 3\alpha }$ ${\displaystyle A}$ ${\displaystyle {\overline {GH}}}$ ${\displaystyle E}$ ${\displaystyle {\overline {AP}}}$ ${\displaystyle A'}$ ${\displaystyle A}$ ${\displaystyle I}$ ${\displaystyle {\overline {GH}}}$

Finally (see picture 4) the fold from through and the one from through . The fold lines and divide the angle into three (exactly) equal parts. ${\displaystyle A}$ ${\displaystyle I}$ ${\displaystyle A}$ ${\displaystyle A'}$ ${\displaystyle {\overline {AG'}}}$ ${\displaystyle {\overline {AA'}}}$ ${\displaystyle 3\alpha }$

• 

  Image 1
  Fold the first two fold lines, it doesn't have to be in the middle of the sheet ${\displaystyle {\overline {EF}}}$

• 

  Image 2
  The third fold provides the angle ${\displaystyle 3\alpha }$

• 

  Image 3
  The crucial fourth fold, corner up and down ${\displaystyle A}$ ${\displaystyle {\overline {GH}}}$ ${\displaystyle E}$ ${\displaystyle {\overline {AP}}}$

• 

  Photo 4
  The fold lines and divide the angle into three equal parts ${\displaystyle {\overline {AG'}}}$ ${\displaystyle {\overline {AA'}}}$ ${\displaystyle 3\alpha }$

Use a flexible ruler to divide the angle into three parts

In this method, a helix is applied to a cylindrical surface , which is intersected by a three-dimensional line at four points. The two inner intersection points divide the angle given by the two outer ones. On closer inspection one sees the similarity of the construction with the method Quadratrix of Hippias . Instead of the Euclidean tools - compasses and ruler - a cylindrical body with a given circle center of the cylinder, a flexible ruler (e.g. tape measure ) and, alternatively, e.g. B. used a stop bracket. ${\displaystyle M}$

method

First of all, the angle leg is drawn in from the center of the circle (see Figure 1) and the angle to be third is determined using the angle leg . The two (red) lines are then drawn in and on the outer surface using the flexible ruler or, alternatively, e.g. B. using a (right-angled) stop bracket. ${\displaystyle M}$ ${\displaystyle {\overline {MA}}}$ ${\displaystyle 3\alpha }$ ${\displaystyle {\overline {MB}}}$ ${\displaystyle {\overline {AC}}}$ ${\displaystyle {\overline {BD}}}$

The next step is to apply the helical line (green) to the cylindrical surface (see Fig. 2). The flexible ruler is placed on the edge of the cylinder and fixed. This is followed by five windings with the same pitch, which corresponds to the width of the ruler. The helix is ​​drawn in step by step, on the free edge of the ruler. Now the intersections with the first winding of the helix and with the fourth winding are marked. ${\displaystyle h,}$ ${\displaystyle E}$ ${\displaystyle F}$

The flexible ruler is now placed on the cylindrical surface (see Figure 3) so that the edge of the ruler (light blue) runs through the points and , while the intersection points and are marked on the helical line. In this case, this line - also a helix with a very large pitch - the shortest distance of the two points and conclusion are using the flexible ruler, or alternatively z. B. using a stop bracket, the routes and as well as and entered. ${\displaystyle E}$ ${\displaystyle F}$ ${\displaystyle G}$ ${\displaystyle I}$ ${\displaystyle E}$ ${\displaystyle F.}$ ${\displaystyle {\overline {IJ}}}$ ${\displaystyle {\overline {JM}}}$ ${\displaystyle {\overline {GH}}}$ ${\displaystyle {\overline {HM}}}$

Because of this , the angle is divided into exactly three parts. ${\displaystyle |AJ|=|JH|=|HB|}$ ${\displaystyle 3\alpha }$

• 

  Figure 1
  Drawing of the angle and of the two (red) routes and using the flexible ruler or alternatively a (rectangular) stop bracket ${\displaystyle 3\alpha }$ ${\displaystyle {\overline {AC}}}$ ${\displaystyle {\overline {BD}}}$

• 

  Fig. 2
  Draw the screw line (green) on the outer surface with the help of the flexible ruler

• 

  Figure 3
  Draw a three-dimensional line with the help of the flexible ruler, project the inner intersection points with the helical line and onto the circular area ${\displaystyle G}$ ${\displaystyle I}$

Approximation method

Albrecht Dürer's approximation of the division into three

Three-way division of the angle, an approximate construction according to Dürer

In 1906, Karl Hunrath published a study of Dürer's approximate solution of the three-dimensional division of angles from 1525 in the journal Heidelberger Texte zur Mathematikgeschichte .

Construction description

In a given sector of a circle with a center point and a center point angle larger , the chord is divided into and thirds. This is followed by the erection of the two perpendiculars in and , which results in the intersection points or with the circular arc . Now a circular arc with the radius ab and a second one with the radius ab is drawn until they cut into or into the chord . After thirds of the way close to the point and the line close to the point , the points of intersection or the projection of the points and to the circular arc which are points supplies and the connecting lines (red) with and and divide the center angle in approximately three equal parts. ${\displaystyle O}$ ${\displaystyle \angle {AOB}}$ ${\displaystyle 90^{\circ }}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle C}$ ${\displaystyle D}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle C}$ ${\displaystyle D}$ ${\displaystyle E}$ ${\displaystyle F}$ ${\displaystyle {\overline {AE}}}$ ${\displaystyle E}$ ${\displaystyle {\overline {BF}}}$ ${\displaystyle F}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle E_{1}}$ ${\displaystyle F_{1}}$ ${\displaystyle {\overline {CE_{1}}}}$ ${\displaystyle E_{1}}$ ${\displaystyle {\overline {DF_{1}}}}$ ${\displaystyle F_{1}}$ ${\displaystyle G_{1}}$ ${\displaystyle H_{1}.}$ ${\displaystyle G_{1}}$ ${\displaystyle H_{1}}$ ${\displaystyle G}$ ${\displaystyle H.}$ ${\displaystyle G}$ ${\displaystyle O}$ ${\displaystyle H}$ ${\displaystyle O}$ ${\displaystyle \angle AOB}$

This result is achieved with two iteration steps . After the first iteration, the angles and result ${\displaystyle \angle {EOA},}$ ${\displaystyle \angle {FOE}}$ ${\displaystyle \angle {BOF}.}$

The points drawn in and the line in the middle are not required for the construction, they only serve the proof discussed in detail by Hunrath. ${\displaystyle K,L,M,N}$ ${\displaystyle Q}$ ${\displaystyle {\overline {OI}}}$

Error consideration

Dürer's approximate solution shows only very small absolute errors for angles ${\displaystyle 0^{\circ }<2\alpha \leq 180^{\circ }}$ ${\displaystyle F_{a}.}$

Trisection of the angle according to Dürer's absolute error of the angle ${\displaystyle 2\alpha }$ ${\displaystyle F_{a}}$ ${\displaystyle \beta =\angle GOA=\angle BOH}$
angle ${\displaystyle 2\alpha }$	angle ${\displaystyle 2\alpha /3}$	angle ${\displaystyle \beta }$	${\displaystyle F_{a}}$
0 ${\displaystyle 30^{\circ }}$	${\displaystyle 10^{\circ }}$	0 ${\displaystyle 9^{\circ }\;59'\;59{,}992''}$	${\displaystyle -0{,}007''}$
0 ${\displaystyle 45^{\circ }}$	${\displaystyle 15^{\circ }}$	${\displaystyle 14^{\circ }\;59'\;59{,}879''}$	${\displaystyle -0{,}12''}$
0 ${\displaystyle 60^{\circ }}$	${\displaystyle 20^{\circ }}$	${\displaystyle 19^{\circ }\;59'\;59{,}093''}$	${\displaystyle -0{,}906''}$
0 ${\displaystyle 90^{\circ }}$	${\displaystyle 30^{\circ }}$	${\displaystyle 29^{\circ }\;59'\;44{,}504''}$	${\displaystyle -15{,}495''}$
${\displaystyle 120^{\circ }}$	${\displaystyle 40^{\circ }}$	${\displaystyle 39^{\circ }\;58'\;4{,}427''}$	${\displaystyle -1'\;55{,}572''}$
${\displaystyle 150^{\circ }}$	${\displaystyle 50^{\circ }}$	${\displaystyle 49^{\circ }\;50'\;56{,}209''}$	${\displaystyle -9'\;3{,}79''}$
${\displaystyle 180^{\circ }}$	${\displaystyle 60^{\circ }}$	${\displaystyle 59^{\circ }\;28'\;22{,}498''}$	${\displaystyle -31'\;37{,}501''}$

Approximation through iterative bisection of the angle

This less efficient but much simpler method uses the geometric series

${\displaystyle {\frac {\alpha }{3}}=\alpha \cdot \left({\frac {1}{2}}-{\frac {1}{4}}+{\frac {1}{8}}-{\frac {1}{16}}+{\frac {1}{32}}-{\frac {1}{64}}+\dots \right)}$

Example angle after nine iterations ${\displaystyle 60^{\circ }}$

${\displaystyle 60^{\circ }\cdot \left({\frac {1}{2}}-{\frac {1}{4}}+{\frac {1}{8}}-{\frac {1}{16}}+{\frac {1}{32}}-{\frac {1}{64}}+{\frac {1}{128}}-{\frac {1}{256}}+{\frac {1}{512}}\right)=60^{\circ }\cdot {\frac {171}{512}}=20{,}0390625^{\circ }}$

It should be noted that the following formula applies:

${\displaystyle \sum _{k=1}^{n}{\frac {(-1)^{k-1}}{2^{k}}}={\frac {1}{3}}-{\frac {(-1)^{n}}{3\cdot 2^{n}}}.}$

There is thus also an indirect connection with the representation in the binary system . ${\displaystyle {\frac {1}{3}}=[0{,}010101\dots ]_{2}=[0{,}{\overline {01}}]_{2}}$

Approximation for angles greater than 0 ° to 90 °

In 2011, Chris Alberts sent an extraordinarily good approximation of an angle trisection to Rouben Rostamian ( University of Maryland, Baltimore County ).

Rostamian reformulated and rearranged Alberts' construction, but the differences from the original, he says, are only cosmetic. At the beginning of the construction description he refers to an explanation ("Explanation here"), in which he also shows the reasons why no pictures of this construction can be seen. Nonetheless, the construction shown below is feasible with the help of Rostamian's description alone.

Approximate construction for angles greater than 0 ° to 90 ° according to Chris Alberts

Animation with step sizes approx. 3 °, for the sake of clarity the points are not labeled

construction

(Translation)

Look at the arc on the circle that is centered in (see picture). Assuming the angle is between and degrees, then do the following to divide: ${\displaystyle AB}$ ${\displaystyle C}$ ${\displaystyle O}$ ${\displaystyle \angle {AOB}}$ ${\displaystyle 0}$ ${\displaystyle 90}$ ${\displaystyle \angle {AOB}}$

1. Draw the circle around with a radius the intersection points with the lines or are or ${\displaystyle {C'}}$ ${\displaystyle O}$ ${\displaystyle {\tfrac {1}{3}}{\overline {OA}};}$ ${\displaystyle {\overline {OA}}}$ ${\displaystyle {\overline {OB}}}$ ${\displaystyle {A'}}$ ${\displaystyle {B'}.}$
2. Draw the circle (shown in green) through the point ${\displaystyle {C''}}$ ${\displaystyle {B'}}$ ${\displaystyle O.}$
3. Let it be the midpoint of the segment Draw a line from parallel to through the circular line from to the circle where the intersection points are or ${\displaystyle E}$ ${\displaystyle {\overline {OB'}}.}$ ${\displaystyle E}$ ${\displaystyle {\overline {OA}}}$ ${\displaystyle {C''}}$ ${\displaystyle {C'};}$ ${\displaystyle P}$ ${\displaystyle R.}$
4. Let it be the midpoint of the line. Draw a line through until it intersects the circle in . ${\displaystyle M}$ ${\displaystyle {\overline {PR}}.}$ ${\displaystyle {B'}}$ ${\displaystyle M,}$ ${\displaystyle {C'}}$ ${\displaystyle N}$
5. Draw a line parallel to and pick the point on it so that is. ${\displaystyle {B'}}$ ${\displaystyle {\overline {OA}}}$ ${\displaystyle F}$ ${\displaystyle {\overline {NB'}}={\overline {NF}}}$
6. Extend the route until the circle in cuts. ${\displaystyle {\overline {NF}},}$ ${\displaystyle C}$ ${\displaystyle G}$
7. Draw the line and extend it until it intersects the circle in . ${\displaystyle {\overline {GO}}}$ ${\displaystyle {C'}}$ ${\displaystyle {H}}$

Note: If you look closely at the drawing, you can see that the lines and do not overlap, i.e. H. are not collinear . ${\displaystyle {\overline {GO}}}$ ${\displaystyle {\overline {GN}}}$

8. Let it be diametrically opposite the point in the circle. Draw a line parallel to and choose the point on it so that the distance is. ${\displaystyle D}$ ${\displaystyle {B'}}$ ${\displaystyle {C'}.}$ ${\displaystyle D}$ ${\displaystyle {\overline {OA}}}$ ${\displaystyle J}$ ${\displaystyle |HD|={\overline {HJ}}}$

Note: The route is not an extension of the route ${\displaystyle {\overline {HJ}}}$ ${\displaystyle {\overline {GH}}.}$

9. Extend the route until the circle in cuts. ${\displaystyle {\overline {HJ}},}$ ${\displaystyle C}$ ${\displaystyle K}$
10. Reflect on the track to get the point . ${\displaystyle K}$ ${\displaystyle {\overline {OA}},}$ ${\displaystyle T}$

The angle is almost equal to one third of the angle ${\displaystyle \angle {AOT}}$ ${\displaystyle \angle {AOB}.}$

Failure analysis

Rostamian carried out an error analysis, among other things with the following results: The above construction steps (1. – 10.) Contain three levels of approximation, i. H. three different error sizes in the range between and : ${\displaystyle 0^{\circ }}$ ${\displaystyle 90^{\circ }}$

• Step 1: After the 5th step, the difference between the angle and an angle that is exactly one third is max. ${\displaystyle \angle {F{B'}N}}$ ${\displaystyle 0{,}7^{\circ }.}$
• Step 2: After the 7th step, the difference between the angle and an angle that is exactly one third is only max. ${\displaystyle \angle {{A'}OH}}$ ${\displaystyle 0{,}00013791^{\circ }.}$
• Step 3: After the 10th step, the angle has the excellent small difference value of max. ${\displaystyle \angle {AOT}}$ ${\displaystyle \left(1{,}33\cdot 10^{-16}\right)^{\circ }.}$

The construction shown was made with the dynamic geometry software (DGS) GeoGebra ; In this case, the degrees are displayed with a significant thirteen decimal places. The very small errors of the angle, in other words, the differences are therefore always displayed by GeoGebra . ${\displaystyle \angle {AOT},}$ ${\displaystyle {\tfrac {\alpha }{3}}-\beta ,}$ ${\displaystyle 0^{\circ }}$

Clarification of the absolute error

The difference value of max. Corresponds to an absolute error of the - not shown - chord which results as follows: ${\displaystyle \left(1{,}33\cdot 10^{-16}\right)^{\circ }}$ ${\displaystyle F}$ ${\displaystyle {\overline {AT}},}$

${\displaystyle F=2\cdot \sin \left({\frac {\left(1{,}33\cdot 10^{-16}\right)^{\circ }}{2}}\right)=0{,}00000000000000000232\ldots =2{,}32\ldots \cdot 10^{-18}\;[\mathrm {LE} ]}$

Clearly: if the length of the angled legs were equal to 1 billion  km (the light would need almost 39 days for this distance), the absolute error of the tendon would be approx. 2.32 mm. ${\displaystyle {\overline {AT}}}$

Applications

A cubic equation with real coefficients can be solved geometrically with a pair of compasses, ruler and an angular three-parter (i.e. their solutions are constructed) if and only if it has three real solutions. The coefficients of the polynomial are taken as given and used in the construction. In particular, the cube root of 2, which is required when doubling the cube , cannot be constructed using these tools, since the equation does not have exclusively real solutions. ${\displaystyle x^{3}-2=0}$

A regular polygon with sides can be constructed with a ruler, pair of compasses and angled three- parter if and only if different Fermat's prime numbers are greater than 3 of the form , cf. also Pierpont prime number . ${\displaystyle n}$ ${\displaystyle n=2^{r}3^{s}p_{1}\cdots p_{k}}$ ${\displaystyle p_{j}}$ ${\displaystyle p_{j}=2^{t}3^{u}+1}$

With the help of the cubic equation of the heptagon , the following example explains how the cosine of the angle can be found, which can be divided into thirds with the help of a so-called additional tool (e.g. tomahawk).

The heptagon has the cubic equation

${\displaystyle (1)\;\;X^{3}+X^{2}-2X-1=0.}$

If one sets results as a solution of ${\displaystyle X={\tfrac {\left(Y-1\right)}{3}},}$ ${\displaystyle 1+6\cdot \cos({\tfrac {2\pi }{7}})}$ ${\displaystyle (=1+3\eta )}$

${\displaystyle (2)\;\;Y^{3}-21Y-7=0.}$

By inserting

${\displaystyle Y={\sqrt {28}}\cdot \cos(\theta )}$

it simplifies to

${\displaystyle 7\cdot {\sqrt {28}}\left(4\cdot \cos ^{3}(\theta )-3\cdot \cos(\theta )\right)=7;}$

finally we get the cosine of the angle, which can be divided into thirds:

${\displaystyle \cos(3\theta )={\frac {1}{\sqrt {28}}}}$.

The following describes how the cubic equation is based on the example of a heptagon

${\displaystyle (1)\;\;X^{3}+X^{2}-2X-1=0}$

is determined. It starts by drawing a regular heptagon.

Construction description

Heptagon according to Andrew M. Gleason, construction sketch for determining the angle that can be divided into three with an additional aid. ${\displaystyle 3\theta ,}$

1. Perimeter of the heptagon with the radius around the zero point of a Cartesian coordinate system . ${\displaystyle r=6}$ ${\displaystyle O}$
2. Mark the points and ${\displaystyle A(6|0),P(-1|0),Q(-3|0)}$ ${\displaystyle R(3|0).}$
3. An arc with a radius cuts into the axis and the line is the side of an equilateral triangle with a radius ${\displaystyle {\overline {RQ}}}$ ${\displaystyle y}$ ${\displaystyle K(0|{\sqrt {27}})}$ ${\displaystyle L(0|-{\sqrt {27}});}$ ${\displaystyle {\overline {KL}}}$ ${\displaystyle {\overline {RQ}}.}$
4. Connection of the points with and with the angle corresponds ${\displaystyle P}$ ${\displaystyle K}$ ${\displaystyle P}$ ${\displaystyle L;}$ ${\displaystyle \angle {APK}}$ ${\displaystyle 3\theta .}$
5. Arc around with radius ${\displaystyle P}$ ${\displaystyle {\overline {PK}}.}$
6. Tripartite the angle using z. B. a tomahawk, gives the point of intersection ${\displaystyle 3\theta ,}$ ${\displaystyle S.}$
7. Parallel to through results in the points of intersection and and are corner points of the regular heptagon (not shown) ${\displaystyle {\overline {KL}}}$ ${\displaystyle S}$ ${\displaystyle B,T}$ ${\displaystyle G;}$ ${\displaystyle B}$ ${\displaystyle G}$ ${\displaystyle ABCDEFG.}$

Proof of construction

Let be the intersection of the line with the axis. The construction shows that ${\displaystyle U}$ ${\displaystyle {\overline {ST}}}$ ${\displaystyle x}$

${\displaystyle {\overline {PK}}={\sqrt {28}},\;\;\cos \left(\angle {APK}\right)={\frac {1}{\sqrt {28}}},\;\;{\overline {PU}}={\sqrt {28}}\cdot \cos \left(\angle {APS}\right)={\sqrt {28}}\cdot \cos \left({\frac {1}{3}}\angle {APK}\right).}$

The construction is correct if

${\displaystyle {\overline {OU}}=6\cdot \cos \left({\frac {2\pi }{7}}\right);}$  or equivalent if   ${\displaystyle {\overline {PU}}=1+6\cdot \cos \left({\frac {2\pi }{7}}\right),}$

where the normalization of the cosine by the factor results from the choice of the radius . So you only have to determine the following identity: ${\displaystyle 6}$ ${\displaystyle r=6}$

${\displaystyle {\sqrt {28}}\cdot \cos \left({\frac {1}{3}}\arccos \left({\frac {1}{\sqrt {28}}}\right)\right)=1+6\cdot \cos \left({\frac {2\pi }{7}}\right).}$

To do this, be

${\displaystyle \xi =\cos \left({\frac {2\pi }{7}}\right)+i\cdot \sin \left({\frac {2\pi }{7}}\right)}$

a primitive seventh root of unity in . Sit down ${\displaystyle \mathbb {C} }$

${\displaystyle \eta =\xi +\xi ^{-1}=2\cdot \cos \left({\frac {2\pi }{7}}\right),}$

then

${\displaystyle \eta ^{3}+\eta ^{2}-2\eta -1=\xi ^{3}+\xi ^{2}+\xi +1+\xi ^{-1}+\xi ^{-2}+\xi ^{-3}=0.}$

Thus is a root of the cubic equation ${\displaystyle \eta }$

${\displaystyle (1)\;\;X^{3}+X^{2}-2X-1=0.}$

As described above, this gives the cosine of the angle : ${\displaystyle 3\theta }$

${\displaystyle \cos(3\theta )={\frac {1}{\sqrt {28}}}.}$

Morley's theorem

Morley's theorem, construction sketch

Even if at first it appears that Morley's theorem is suitable for the trisection of any angle, this is not the case.

In a given triangle , the angles at the vertices and are divided into thirds first. This requires an additional tool, e.g. B. a dynamic geometry software (DGS) . The precisely generated three -part angles (red) provide the corner points , and of the Morley triangle. ${\displaystyle ABC}$ ${\displaystyle A,B}$ ${\displaystyle C}$ ${\displaystyle D}$ ${\displaystyle E}$ ${\displaystyle F}$

Morley's Theorem:

"The three points of intersection of the three adjacent three-cornered angles of any triangle form an equilateral triangle."

- Horst Hischer : The Morley triangle between application and play

literature

• Ernst-Erich Doberkat: The tripartite division of the angle. In: Die Drei (pp. 59–85), Springer Verlag, 2019.
• Underwood Dudley : The Trisectors. Mathematical Association of America, 1996.
• Underwood Dudley: A budget of trisections. Springer Verlag, 1987.
• Christoph Scriba , Peter Schreiber : 5000 years of geometry. Springer Verlag, 2010.

Web links

Wikiversity: Proof of Impossibility for Trisectioning the Angle  - Course Materials

Commons : trisection of the angle  - collection of images

• Eric W. Weisstein : Angle Trisection . In: MathWorld (English).
• Jim Loy: Trisection of an Angle ( Memento from January 1, 2014 in the Internet Archive )
• Matroids Math Planet: Trisection and Haga's Theorem.
• Swiss television: Origami solves unsolvable problems. Einstein , April 9, 2009.
• Sarah Kuchar: The trisection of the angle - a journey through time. January 10, 2016.

Individual evidence

1. ↑ Jürgen Köller: Constructible three-partitions. Tripartite an angle. 2009, accessed April 23, 2021 . 
2. ↑ Hans Walser: 5 Constructibility, 5.1 degrees. Angle measurement. August 22, 2013, accessed April 10, 2021 . 
3. ↑ Johann Cigler : 1. The main clause of the Galois theory. Solids - rings - equations. In: univie.ac.at. University of Vienna, accessed on March 26, 2021 . 
4. ↑ ^{a b c} Christoph Scriba , Peter Schreiber : 5000 years of geometry. Springer, 2010, p. 44.
5. ↑ Markus Asper: 1. The beginnings: from Miletus to Athens. (PDF) Mathematics, milieu, text. Early Greek mathematics and their environment. Sudhoff's archive. Journal for the History of Science, 2003, p. 13 , accessed April 13, 2021 . 
6. ↑ A. Jackter: History of Mathematics. In: The Problem of Angle Trisection in Antiquity. Rutgers University Press, 2000, accessed November 27, 2020 . 
7. ↑ Christoph Scriba, Peter Schreiber: 5000 years of geometry. Springer, 2010, p. 78.
8. ↑ ^{a b} Horst Hischer : 1 connection between quadratrix and trisectrix. (PDF) History of Mathematics as a Didactic Aspect (2). Solution of classic problems. In: horst.hischer.de. 1994, p. 279 , accessed March 31, 2021 . 
9. ↑ Christoph Scriba, Peter Schreiber: 5000 years of geometry. Springer, 2010, p. 70.
10. ↑ K. Matter: On the trisection of the angle → Fig. B. In: Communications from the Thurgau Natural Research Society . tape 25 , 1902, pp. 22nd ff . ([ online on ZOBODAT Online] [PDF; accessed April 1, 2021]).
11. ↑ Christoph Scriba, Peter Schreiber: 5000 years of geometry. Springer, 2010, p. 46.
12. ↑ K. Matter: On the trisection of the angle, → see last paragraph . In: Communications from the Thurgau Natural Research Society . tape 25 , 1902, pp. 22 ([ online on ZOBODAT Online] [PDF; accessed April 1, 2021]).
13. ↑ Christoph Scriba, Peter Schreiber: 5000 years of geometry. Springer, 2010, p. 77.
14. ↑ ^{a b c} Dietmar Herrmann: The ancient mathematics. A history of Greek mathematics, its problems and solutions, Springer-Verlag, 2013, p. 155, point 3. ( limited preview in Google book search), accessed on August 21, 2020.
15. ^ ^{A b} Robert C. Yates: THE TRISECTION PROBLEM, 3. The Hyperbola. In: ERIC. National Council of Teachers of Mathematics, Inc., Washington, DC, 1971, pp. 32-33 , accessed March 31, 2021 . 
16. ↑ Katharina Wieser: 5.2.6. Arab mathematicians with hyperbolic neusis. The three classic mathematical problems of antiquity: cube doubling, angular trisection and circular quadrature. Johannes Kepler University Linz, March 2013, p. 58 , accessed on April 7, 2021 . 
17. ↑ Katharina Wieser: 5.2.6. Arab mathematicians with hyperbolic neusis. The three classic mathematical problems of antiquity: cube doubling, angular trisection and circular quadrature. Johannes Kepler University Linz, March 2013, p. 59 , accessed on April 7, 2021 . 
18. ↑ Christoph Scriba, Peter Schreiber: 5000 years of geometry. Springer, 2010, p. 179.
19. ↑ Christoph Scriba, Peter Schreiber: 5000 years of geometry. Springer, 2010, p. 180.
20. ↑ F. Vogel: About the approximate constructions for the tripartite division of an angle. Magazine f. math. and natural sciences Education, 62nd year, 1931, pp. 145–155.
21. ↑ ^{a b} Karl Hunrath: Dürer approximate trisection a circular arc. Bibliotheca Mathematica. Journal of the History of Mathematical Sciences. University of Heidelberg, 1906, p. 120 , accessed on April 12, 2021 . 
22. ↑ Christoph Scriba, Peter Schreiber: 5000 years of geometry. Springer, 2010, p. 283.
23. ↑ Jesper Lützen: Why was Wantzel overlooked for a century? The changing importance of an impossibility result. Historia Mathematica 36, ​​2009, p. 387.
24. ↑ Christoph J. Scriba, Peter Schreiber: 5000 years of geometry. Springer-Verlag, Third Edition, 2010, p. 405.
25. ^ ^{A b} Pierre Wantzel : Recherches sur les moyens de reconnaître si un Problème de Géométrie peut se résoudre avec la règle et le compas (=  Journal de mathématiques pures et appliquées (Liouville's Journal) . Volume 2 ). 1837, p. 366-372 ( PDF ).
26. ↑ Craig Smorynski: History of Mathematics: A Supplement . Springer, 2007, ISBN 978-0-387-75480-2 , pp. 130 ( Google Books ). For the historical classification of Wantzel's evidence in the earlier work of Ruffini and Abel and for a temporal comparison with Galois.
27. ↑ Jesper Lützen: Why was Wantzel overlooked for a century? The changing importance of an impossibility result. Historia Mathematica 36, ​​2009, pp. 378-379.
28. ↑ Jesper Lützen: Why was Wantzel overlooked for a century? The changing importance of an impossibility result. Historia Mathematica 36, ​​2009, p. 379.
29. ↑ Jesper Lützen: Why was Wantzel overlooked for a century? The changing importance of an impossibility result. Historia Mathematica 36, ​​2009, p. 391.
30. ↑ Hans Humenberger : Elementary mathematical considerations on the Delic problem and on the three-dimensional division . In: Internat. Math. News No. 219, 25-43 . 2012, p. 38–40 ( online [PDF; accessed November 14, 2020]).
31. ↑ ^{a b} Falko Lorenz : Algebra Volume I: Fields and Galois Theory. Springer, p. 52.
32. ↑ K. Robin McLean: Trisecting angles with ruler and compasses. Mathematical Gazette. 92, pp. 320-323.
33. ^ Underwood Dudley : What to do when the trisector comes. Missouri University of Science and Technology, 1983, accessed November 21, 2020 .  See also Mathematical Intelligencer , Volume 5, 1983, No. 1, and in his book on it.
34. ↑ Hans Humenberger: 8 constructions using a marked ruler and paper folds (origami). Elementary mathematical considerations on the Delic problem and the three-dimensional division of angles. University of Vienna, 2012, pp. 41–42 , accessed on April 13, 2021 . 
35. ↑ Bodo v. Pape: 7.4 Tripartite with the Tomahawk. In: Macro Mathematics. Beyond Algebra and Analysis: Algorithms. BoD - Books on Demand, 2016, ISBN 373579419X ( limited preview in Google Book Search)
36. ↑ ^{a b c d} Ludwig Bieberbach : On the teaching of cubic constructions, journal for pure and applied mathematics. H. Hasse and L. Schlesinger, Volume 167, Walter de Gruyter, Berlin 1932, pp. 142–146, DigiZeitschriften , corresponding formulas on p. 143 and 144 image on p. 144 , accessed on June 6, 2018.
37. ↑ K. Matter: To the trisection of the angle . In: Communications from the Thurgau Natural Research Society . tape 25 , 1902, pp. 20 ([ online on ZOBODAT Online] [PDF; accessed on March 27, 2021]).
38. ↑ K. Matter: To the trisection of the angle . In: Communications from the Thurgau Natural Research Society . tape 25 , 1902, pp. 21 ff . ([ online on ZOBODAT Online] [PDF; accessed on March 24, 2021]).
39. ↑ K. Matter: To the trisection of the angle . → Fig.a. Dividing an angle into three with the help of a hyperbola. In: Communications from the Thurgau Natural Research Society . tape 25 , 1902 ([ online on ZOBODAT Online] [PDF; accessed on July 29, 2020]).
40. ↑ Justin Seago: The Maclaurin Trisectrix. CR College of the Redwoods, December 8, 2008, accessed September 1, 2020 . 
41. ↑ Matthias Sebastian Konzett: 3.5.1. Solution using origamics. Impossible possible? University of Vienna, September 3, 2012, p. 46 ff. , Accessed on November 23, 2020 . 
42. ^ ^{A b} Greg Blonder: Trisecting the angle with a straightedge. + plus. magazine, accessed April 9, 2021 . 
43. ↑ Albrecht Dürer: Underweysung the measurement with the zirckel and Richtscheyt, level in lines and whole corpora. Bavarian State Library, Digital Collections, 1525, accessed on April 12, 2021 . 
44. ↑ Karl Hunrath: Albrecht Durer approximate threefold division of an arc. Bibliotheca Mathematica. Journal of the History of Mathematical Sciences. University of Heidelberg, 1906, p. 121 , accessed on April 11, 2021 . 
45. ↑ Karl Hunrath: Albrecht Durer approximate threefold division of an arc. Bibliotheca Mathematica. Journal of the History of Mathematical Sciences. University of Heidelberg, 1906, p. 122 ff. , Accessed on April 11, 2021 . 
46. ↑ Jim Loy: Trisection of an Angle. To analogy: (last paragraph). In: jimloy.com. Archived from the original on February 25, 2012 ; accessed on March 27, 2021 (English). 
47. ↑ ^{a b c} Rouben Rostamian: An angle trisection. University of Maryland, Baltimore County, March 23, 2011, accessed February 3, 2020 . 
48. ↑ Andrew M. Gleason : Angle Trisection, the Heptagon and the Triskaidecadon. The American Mathematical Monthly, Vol. 95, Issue 3, p. 190.
49. ↑ Andrew M. Gleason: Angle Trisection, the Heptagon and the Triskaidecadon. The American Mathematical Monthly, Vol. 95, Issue 3, p. 191.
50. ↑ Andrew M. Gleason: Angle Trisection, the Heptagon, and the Triskaidecagon. (PDF) The American Mathematical Monthly. Florida Atlantic University, March 1988, p. 187 , accessed April 6, 2021 . 
51. ^ ^{A b c} Andrew M. Gleason: Angle Trisection, the Heptagon, and the Triskaidecagon. (PDF) The American Mathematical Monthly. Florida Atlantic University, March 1988, p. 186 , accessed April 6, 2021 . 
52. ↑ Horst Hischer: 1.1.2 The Morley triangle between application and game. Fundamental terms of mathematics: Origin and development: structure - function - number. Springer-Verlag, June 13, 2012, pp. 2-4 , accessed on April 5, 2021 . 

This article was added to the list of excellent articles on April 14, 2021 in this version .