Cube doubling

The doubling the cube , also known as Delos problem , refers to the geometric task of a given cube a second cube with twice the volume to construct . The problem belongs to the three " classical problems of ancient mathematics " and was already in the 5th century BC. . BC in ancient Greece formulated.

An initial cube with the edge length (a so-called unit cube ) has the volume Another cube has the edge length and the volume The new edge length is the cube root of , that is . This can be determined by means of infinitesimal calculus , but cannot be constructed in finitely many steps from the distances 0 and 1 using a compass and ruler . So if one tries to work on the problem of doubling the cube exclusively with the tools that Euclid has in his elements ${\displaystyle a=1}$ ${\displaystyle V=1^{3}=1.}$ ${\displaystyle x}$ ${\displaystyle V=x^{3}=2=2\cdot 1^{3}.}$ ${\displaystyle x}$ ${\displaystyle 2}$ ${\displaystyle {\sqrt[{3}]{2}}=1{,}259921\ldots }$used, namely with a pair of compasses and an unmarked ruler, it cannot be solved. This statement can be translated into the language of algebra , whereby a mathematical proof of the impossibility of the construction can ultimately be given. One such was first carried out by the French mathematician Pierre Wantzel in 1837. However, it is very likely that Carl Friedrich Gauß already knew a proof earlier, but did not write it down.

Identical problems exist when the cube volume is increased to 3, 4, 5, 6 and 7 times the original volume. On the other hand, the task of, for example, an eight-fold increase in volume is not a problem because the cube root of 8 can be calculated without any problems and the resulting doubling of the edge length is easy to do.

If the restriction is weakened and an additional aid is allowed, such as corresponding markings on the ruler or special curves, then the construction of a cube with twice the volume is possible. Corresponding processes were already known in antiquity .

History from antiquity

Ratio of volume to edge length of a cube, the starting cube is the unit cube with edge length ${\displaystyle 1}$

The most important ancient source on the doubling of the cube is the comment by the late ancient author Eutokios on Archimedes ' work "About Sphere and Cylinder" ("Περὶ σφαίρας καὶ κυλίνδρου"), in which various approaches by ancient mathematicians are collected. Among other things, a letter from the scholar Eratosthenes (around 275–194 BC) to a King Ptolemy (probably Ptolemy III or Ptolemy IV ) is literally quoted there, which has now been proven to be an authentic reproduction of the original letter and in which the scientist speaks to the ruler on the question of doubling the dice. As the oldest evidence for this mathematical problem, Eratosthenes quotes there "one of the old tragedy poets" ("τῶν ἀρχαίων τινὰ τραγῳδοποιῶν"), in whose work the mythical King Minos had the tomb of his son Glaucus built and instructed the builder to make it twice as big as that make the first draft, but keep the cube shape. Of the three important Athenian tragedy poets of the 5th century BC Chr., Aeschylus , Sophocles and Euripides , we know that they took up the legend of Minos and Glaucos in one of their works; however, it is possible that the quote comes from a tragedy by a completely different poet.

The alternative designation "Delisches Problem" goes back to an episode that Eratosthenes also cites in his letter, but which is also described by various other ancient authors (including Plutarch and Theon of Smyrna ) and which, from an ancient scholarly point of view, is based on an actual historical event could: The residents of the island of Delos asked an oracle for advice during a serious epidemic on what they could do to improve their situation. The oracle had instructed them to double the size of the cube-shaped altar in the island's temple of Apollo - that is, its volume . The Delian architects, however, were at a loss as to how this could actually be done, and then asked Plato (428 / 427–348 / 347 BC) for advice. He referred them to Archytas of Taranto , Eudoxus of Knidos and Menaichmos , who each opened up different approaches to a solution. According to Plutarch, however, Plato criticized their approaches because, according to him, by using mechanical methods they destroy the “good” and elegance of geometry. Interestingly, in Eutocius' Archimedes commentary, Plato is also attributed his own mechanical solution to the Delic problem (see section Plato's mechanical method ). Unless a different Plato is meant than the famous philosopher, according to the prevailing research opinion it is likely to be a wrong attribution.

Similar problems from the construction of altars (however with the problem of doubling a square instead of a cube) existed in Vedic times in India and they gave rise to mathematical discussions ( Sulbasutras ). With the square, the problem of doubling can be solved by the Pythagorean theorem .

Ancient solutions with additional tools

• Hippocrates of Chios (second half of the 5th century BC) was the first to show the decisive approach for a theoretical solution to the problem. He found: The problem of doubling the cube is equivalent to that of determining two mean proportions of two quantities . This means that for a route we search for two routes and so that ${\displaystyle a}$ ${\displaystyle x}$ ${\displaystyle y}$

${\displaystyle {\frac {a}{x}}={\frac {x}{y}}={\frac {y}{2a}}.}$

This entails . ${\displaystyle x={\sqrt[{3}]{2}}\cdot a}$

• Plato (428 / 427–348 / 347 BC) was named by Eutokios as the first to find a mechanical method for solving the doubling of the cube . As already mentioned above, this solution should not come from him.
• Eudoxus (397 / 390–345 / 338 BC) found a solution - so it is reported - by constructing the two middle proportions with the help of unknown curves and their points of intersection.
• Archytas of Taranto († about 355-350 BC) was the first to implement the above-mentioned theorem of Hippocrates with the help of the curve named after him; described in the section Curve of Archytas .
• Menaichmos (around 380-320 BC) found two solutions: one in which a parabola is intersected by a hyperbola , and a second, described in detail in the section Using Special Curves , as the intersection of two parabolas.
• Eratosthenes (around 278–194 BC) describes in his letter to King Ptolemy following his introduction to the history of the Delian problem his own “mechanical method” using an apparatus that he called “mesolabe”.
• Diodes (to 240-180 v. Chr.) Used a named after him for his solution cisoid .

Proof of unsolvability using compasses and ruler

History of evidence

Basically, the mathematicians of antiquity did not just use compasses and rulers to solve problems. The assumption that there was such a methodological restriction turned out to be a modern myth. Pierre Wantzel proved in 1837 that the task is actually unsolvable using compasses and ruler alone. His proof was based on the following algebraic considerations:

1. In the first part of the proof, he argues that if a design problem can be solved with a ruler and compass, “the unknown of the problem can be obtained by solving a series of quadratic equations whose coefficients are rational functions of the parameters of the problem and the The roots of the previous equations are ”. ${\displaystyle p,q,r,...}$

With the "unknown of the problem" z. B. meant the route you are looking for. ${\displaystyle x={\sqrt[{3}]{2}}}$

2. He then showed that every algebraic number is the solution of the last equation of a system ${\displaystyle x_{n}^{0}}$ ${\displaystyle x_{n}^{2}+A_{n-1}x_{n}+B_{n-1}=0}$

${\displaystyle {\begin{aligned}&x_{1}^{2}+Ax_{1}+B=0\\&x_{2}^{2}+A_{1}x_{2}+B_{1}=0\\&\vdots \\&x_{n}^{2}+A_{n-1}x_{n}+B_{n-1}=0\end{aligned}}}$

is, where the coefficients are always in the body by successive adjunction , is always solved by a polynomial of degree with coefficients in . Doing so solves the equation and are the given parameters of the problem. ${\displaystyle A_{m},B_{m}}$ ${\displaystyle \mathbb {Q} (p,q,r,...,x_{1}^{0},...x_{m-1}^{0})}$ ${\displaystyle 2^{n}}$ ${\displaystyle \mathbb {Q} (p,q,r,...)}$ ${\displaystyle x_{j}^{0}}$ ${\displaystyle x_{j}^{2}+A_{j-1}x_{j}+B_{j-1}=0}$ ${\displaystyle p,q,r,...}$

3. Wantzel knew that every algebraic number is the solution of a polynomial with degree of a power of two, if it is chosen to be sufficiently large. Hence, its main result was to show that if the number of equations required were reduced to a minimum, the resulting polynomial is irreducible over . ${\displaystyle \mathbb {Q} (p,q,r...)}$

The impossibility of the construction now follows as a corollary from sentences 1 to 3: If, starting with the unit cube, the construction of the doubling of the cube with compasses and ruler would be possible, then there would have to be the zero of an irreducible polynomial above , which has a power of two as degree. The polynomial is irreducible over , but has degree 3. This is a contradiction. ${\displaystyle {\sqrt[{3}]{2}}}$ ${\displaystyle \mathbb {Q} (0,1)=\mathbb {Q} }$ ${\displaystyle x^{3}-2}$ ${\displaystyle \mathbb {Q} }$

It should be noted that Wantzel's original publication is viewed by the mathematician Jesper Lützen as incomplete and difficult to understand - this applies above all to the “proof” of main proposition 3. Lützen closed the gaps afterwards and the results as described above , formulated in modern technical language. Wantzel's proof of the impossibility of constructing the doubling of the cube and the tripartite division of the angle with a ruler and compass was forgotten for almost a century after its publication in 1837. According to Lützen, the “lack of notoriety of the author”, the “fact that some of his contemporaries regarded the result as known or even proven”, and that “the result was not regarded as an important mathematical result at the time of its publication” driving reasons.

Carl Friedrich Gauß, 1828

Historians doubt that Wantzel was the first to know about evidence , as the young Carl Friedrich Gauß very likely had one. A large part of his work Disquisitiones arithmeticae , published in 1801, is devoted to the question of which conditions a polynomial equation must meet in order to be solvable by square radicals. There you will also find the sentences named after Gauss, with the help of which the unsolvability of most classic tasks can be demonstrated with a compass and ruler. With the techniques he developed, Gauss proved, for example, that the 17-sided can be constructed with a compass and ruler. The math historians Christoph Scriba and Peter Schreiber attribute the fact that, despite this, Wantzel is named and quoted by many authors as the originator of the sentences to the “communication difficulties” of 19th century science .

In today's technical language, the proof is an application of the comprehensive Galois theory (after Évariste Galois , French mathematician) and essentially boils down to the fact that the irrational number cannot be expressed by whole numbers , not by the four basic arithmetic operations and also not by square roots . ${\displaystyle {\sqrt[{3}]{2}}=1{,}259921\ldots }$

Algebraic proof

A unit cube and a cube with volume 2 - this has the side length. It can be shown that this number cannot be obtained from whole numbers via concatenations of basic arithmetic operations such as plus, times, divided or square roots. The latter, however, are exactly the numbers that can be constructed using compasses and rulers, starting with the lines 0 and 1. ${\displaystyle {\sqrt[{3}]{2}}=1{,}2599210498948732...}$

The proof of the impossibility can be carried out in detail using the following ideas from algebra . Let there be a set of points ( complex numbers ), which contain at least 0 and 1, and an arbitrary point . For these considerations, it is important that the complex numbers can be understood as a plane - in contrast to this, the real numbers are simply understood as a straight line. Then it applies that the point can be constructed from the points with a compass and ruler if and only if it lies in a body (where is the body of the complex numbers), which is created by the adjunct of a square root from the body ${\displaystyle M}$ ${\displaystyle z}$ ${\displaystyle z}$ ${\displaystyle M}$ ${\displaystyle E\subset \mathbb {C} }$ ${\displaystyle \mathbb {C} }$

${\displaystyle K:=\mathbb {Q} (M\cup {\overline {M}})\subset \mathbb {C} }$

emerges. Roughly speaking, this is the amount that arises from the formation of all sums, products and quotients from rational numbers . Here is the set of the complex conjugates of and the symbol represents the union of two sets. Adjunction of a square root means that there must be a such that . For example, the adjunction of a square root of the rational numbers shows that is a rational number - correspondingly is the set of all sums, products and quotients of rational numbers with the number . When there is a so-called field extension . The problem of doubling the cube using a pair of compasses and ruler can be reduced to the question of whether the number lies in a subfield of , which can be obtained from successive adjunction of square roots. However, this means that the expansion degree of from a power of 2 must be. But it is ${\displaystyle \mathbb {Q} (M\cup {\overline {M}})}$ ${\displaystyle M\cup {\overline {M}}}$ ${\displaystyle {\overline {M}}=\{{\overline {m}}\mid m\in M\}}$ ${\displaystyle M}$ ${\displaystyle \cup }$ ${\displaystyle w^{2}\in K}$ ${\displaystyle E=K(w)}$ ${\displaystyle \mathbb {Q} ({\sqrt {2}})}$ ${\displaystyle ({\sqrt {2}})^{2}=2}$ ${\displaystyle \mathbb {Q} ({\sqrt {2}})}$ ${\displaystyle {\sqrt {2}}}$ ${\displaystyle E|K}$ ${\displaystyle {\sqrt[{3}]{2}}}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {Q} }$ ${\displaystyle E}$ ${\displaystyle \mathbb {Q} }$

${\displaystyle [\mathbb {Q} ({\sqrt[{3}]{2}}):\mathbb {Q} ]=3\not =2^{n}\qquad {\text{für alle}}\,n\in \mathbb {N} ,}$

which makes it impossible to double the cube with a compass and ruler. That the body expansion is of degree 3 can be seen as follows: The polynomial is irreducible over the whole numbers and has the highest coefficient 1. According to Gauss's lemma, is then already irreducible over the rational numbers. This already has the minimal polynomial of and this has degree 3. This results in the knowledge that every element of the set , consisting of all rational numbers that have been arbitrarily “mixed” with the cube root of 2 by the basic arithmetic operations, is unambiguously as rational Numbers can be written. For example is ${\displaystyle \mathbb {Q} ({\sqrt[{3}]{2}})|\mathbb {Q} }$ ${\displaystyle p(x)=x^{3}-2}$ ${\displaystyle p(x)}$ ${\displaystyle p(x)}$ ${\displaystyle {\sqrt[{3}]{2}}}$ ${\displaystyle \mathbb {Q} ({\sqrt[{3}]{2}})}$ ${\displaystyle a+b{\sqrt[{3}]{2}}+c{\sqrt[{3}]{4}}}$ ${\displaystyle a,b,c}$

${\displaystyle {\frac {{\sqrt[{3}]{2}}+2}{{\sqrt[{3}]{2}}-1}}=4+3\cdot {\sqrt[{3}]{2}}+3\cdot {\sqrt[{3}]{4}}.}$

This becomes a three- dimensional vector space over . ${\displaystyle \mathbb {Q} ({\sqrt[{3}]{2}})}$ ${\displaystyle \mathbb {Q} }$

The same argument can be used to show that even a cube multiplication by a natural factor that is not a cube number cannot be achieved with a compass and ruler. ${\displaystyle n}$

Geometric constructions with mechanical aids

If you take another mechanical aid in addition to the classic (Euclidean) tools, compasses and unmarked rulers, such as a special mechanical tool or a correspondingly marked ruler, the edge length of the cube required to double the cube can theoretically be represented exactly.

With the help of a marked ruler

Constructions with the help of a so-called insertion , also known as Neusis constructions , use a compass as well as a ruler on which a special marking is applied as an additional aid.

• The following Neusis construction, Heinrich Dörrie calls it paper strip construction , is one of the best known.

Image 1: Neusis construction with marked ruler edge (side) of the starting cube
${\displaystyle k=}$

If you denote - as shown in Figure 1 - the edge (side) of the starting cube with , an equilateral triangle with the corners is first constructed. The line from is doubled , resulting in the intersection point. Now the line from is extended. Then a half line is drawn from through . Now place a ruler marked with the point (distance from corner to point corresponds to ) on the drawing. Rotate and slide the ruler until its corner is on the extension of the line , the point marking is on the extension of the line and the edge of the ruler runs through the point . Finally connect the point with ${\displaystyle k}$ ${\displaystyle ABC}$ ${\displaystyle {\overline {AC}}}$ ${\displaystyle A,}$ ${\displaystyle D.}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle B}$ ${\displaystyle D}$ ${\displaystyle B}$ ${\displaystyle Q}$ ${\displaystyle P}$ ${\displaystyle Q}$ ${\displaystyle k}$ ${\displaystyle P}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle Q}$ ${\displaystyle {\overline {BD}}}$ ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle Q.}$

The segment is the edge length of the cube you are looking for with twice the volume of the starting cube. ${\displaystyle {\overline {CQ}}=k\cdot {\sqrt[{3}]{2}}}$

• A lesser known Neusis construction comes from Isaac Newton (Fig. 2), but it is remarkable for its simplicity.

Image 2: Neusis construction with marked ruler edge (side) of the starting cube
${\displaystyle a=}$
${\displaystyle a:x=b:y=c:a={\sqrt[{3}]{2}}}$

It begins with the establishment of a vertical line on a half-straight line . An angular leg with the angular width at the apex follows. Now place a ruler marked with the point (distance from corner to point corresponds to the edge of the starting cube) on the drawing. Turn and slide the ruler until the corner of the ruler is on the angle leg , the point marking is on the half-straight line and the edge of the ruler runs through the point . Finally, connect the point with The point drawn is only used to make it easier to formulate in the following proof. ${\displaystyle {\overline {AB}}}$ ${\displaystyle B}$ ${\displaystyle 30^{\circ }}$ ${\displaystyle B}$ ${\displaystyle C}$ ${\displaystyle D}$ ${\displaystyle C}$ ${\displaystyle a}$ ${\displaystyle D}$ ${\displaystyle C}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle C.}$ ${\displaystyle E}$

The segment is the edge length of the cube you are looking for with twice the volume of the starting cube. ${\displaystyle {\overline {AC}}=a\cdot {\sqrt[{3}]{2}}}$

Proof of correctness

Figure 2 shows that the right triangles (blue) and (green) are similar to each other because of the vertex angle , ${\displaystyle ABC}$ ${\displaystyle CDE}$

consequently applies according to the 2nd ray law

(1) ${\displaystyle a:x=b:y=c:a,}$

right triangle and tangent ${\displaystyle BDE}$ ${\displaystyle 30^{\circ }}$

(2) ${\displaystyle \tan \left(30^{\circ }\right)={\frac {1}{\sqrt {3}}}={\frac {\overline {DE}}{\overline {BE}}}={\frac {x}{b+y}}={\frac {a^{2}}{b\left(a+c\right)}},}$

Parts of equation (2) squared

(3) ${\displaystyle {\frac {1}{3}}={\frac {a^{4}}{b^{2}\left(a+c\right)^{2}}},}$

transformed results

(4) ${\displaystyle b^{2}\left(a+c\right)^{2}=3a^{4},}$

Right triangle according to Pythagorean theorem ${\displaystyle ABC,}$

(5) ${\displaystyle b^{2}=c^{2}-a^{2}}$

Value of (5) inserted into (4)

(6) ${\displaystyle \left(c^{2}-a^{2}\right)\left(a+c\right)^{2}=3a^{4}}$

${\displaystyle =\left(c^{2}-a^{2}\right)\left(a^{2}+2ac+c^{2}\right)}$

${\displaystyle =\left(c^{2}a^{2}+2ac^{3}+c^{4}-a^{4}-2a^{3}c-a^{2}c^{2}\right)}$

transformed results

(7) ${\displaystyle 2ac^{3}+c^{4}=3a^{4}+a^{4}+2a^{3}c=4a^{4}+2a^{3}c}$

after the simplification

(8th) ${\displaystyle c^{3}\left(2a+c\right)=2a^{3}\left(2a+c\right)}$

it finally follows from this

(9) ${\displaystyle c^{3}=2a^{3}.}$

In words:

The volume of the cube with the edge length is equal to twice the volume of the starting cube with the edge length ${\displaystyle c^{3}}$ ${\displaystyle c}$ ${\displaystyle 2a^{3}}$ ${\displaystyle a.}$

Determination of the two mean proportions with the help of a mechanical tool

The use of the two mechanical tools described below provides the so-called two middle proportions and the Hippocrates of Chios. They are required for doubling the starting cube with the edge length . The mean proportional corresponds to the sought-after edge length of the doubled cube. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle a}$ ${\displaystyle x}$ ${\displaystyle a\cdot {\sqrt[{3}]{2}}}$

• The theorem of Hippocrates of Chios is described in the section Construction on Special Curves .

Plato's mechanical method

Cube doubling according to Plato (schematic diagram), = edge length of the starting cube, and = edge length of the doubled cube, animation at the end of 25 s pause.
${\displaystyle a}$ ${\displaystyle b=2a}$ ${\displaystyle x}$

As mentioned in the introduction, Eutokios names Plato as the first to use the following method to solve the problem of doubling the cube. Modern commentators deny Plato this because of his vehement rejection of mechanical aids, but Lattmann describes in his study Mathematical Modeling in Plato between Thales and Euclid from the year 2019 in detail why the solution can rightly be ascribed to Plato.

“Contrary to the communis opino, it is clear that the anecdote of the Delian problem is neither entirely nor partially fictional, but is in all probability historically correct. On this basis, in a second step, the approach to the Delic problem attributed to Plato in the tradition can be examined as a potentially genuine, albeit indirectly transmitted, Plato testimony. "

- Claas Lattmann : 5 doubling without doubling: Plato and the Delic problem, p. 207 last paragraph

The mechanical tool (without a material specification ) has the appearance of a rectangular frame. The two side frame parts are perpendicular to the longer base element. So that the loose ruler can be moved exactly parallel to its opposite, it is guided accordingly in the two side parts. For greater clarity, the tool is in the supervisory shown. In the adjacent drawing, the original, partly Greek point designations were used.

method

First the two given variables and are drawn perpendicular to each other and with extensions from the point . ${\displaystyle a={\overline {B\Gamma }}}$ ${\displaystyle b=2a={\overline {AB}}}$ ${\displaystyle B}$

The tool is now moved in the following way on the drawing (see animation) until the two middle proportions and are found: ${\displaystyle x}$ ${\displaystyle y}$

The inner edge of the basic element always runs through a point and the point always lies on the extension of the line before the point of the ruler is pushed onto the extension of the line . ${\displaystyle {\overline {H\Theta }}}$ ${\displaystyle \Gamma }$ ${\displaystyle H}$ ${\displaystyle {\overline {AB}},}$ ${\displaystyle K}$ ${\displaystyle {\overline {K\Lambda }}}$ ${\displaystyle {\overline {\Gamma B}}}$

As a result, the mechanical tool delivers

Plato's mechanical method,
proof

${\displaystyle {\overline {\Delta E}}={\sqrt {y^{2}+x^{2}}},\,\,{\overline {AE}}={\sqrt {4a^{2}+y^{2}}},\,\,x=a\cdot {\sqrt[{3}]{2}}\,\,}$ and ${\displaystyle \,\,y={\frac {2a}{\sqrt[{3}]{2}}}.}$

proof

Because of the parallelism and four right angles at the apex , the following triangles have the same angles and are therefore similar to each other: ${\displaystyle {\overline {AE}}\parallel {\overline {\Gamma \Delta }}}$ ${\displaystyle B}$

Euclid , elements , 1, 29:

${\displaystyle \triangle {BAE}\sim \triangle {B\Delta \Gamma }\sim \triangle {B\Delta E}}$

Since the vertex has a right angle, the following angles are the same: ${\displaystyle E}$

Euclid, elements, 1, 32:

${\displaystyle \angle {\Delta EB}=\angle {EAB}=\angle {\;\Gamma \Delta B}}$

Because the vertex has a right angle, the following angles are also the same: ${\displaystyle \Delta }$

${\displaystyle \angle {B\Delta E}=\angle {B\;\Gamma \Delta }=\angle {BEA}}$

According to Euclid, elements 6, 4 the proportions are:

${\displaystyle {\overline {B\Delta }}:{\overline {B\Gamma }}={\overline {AB}}:{\overline {BE}}={\overline {BE}}:{\overline {B\Delta }}={\sqrt[{3}]{2}}}$

Eratosthenes' mechanical method

Eratosthenes of Cyrene devised (based on the theorem of Hippocrates) a mechanical tool which he described in the letter to King Ptolemy as one:

"[...] mechanical device for determination, by means of which we will not only find two mean proportions between two given straight lines, but as many as can be arranged to be found."

The mechanical device can be imagined as a box made of wood, bronze or ivory with three very thin tablets in the form of identical right-angled triangles, which can be moved to the right or left with the help of grooves. In a task in which more than two mean proportions are sought for two variables, the required number of triangles is always one greater than the number of mean proportions sought. Eratosthenes had his solution of doubling the cube carved in stone in the temple of the Ptolemies in Alexandria.

Cube doubling according to Eratosthenes (schematic diagram), = edge length of the starting cube, and = edge length of the doubled cube, animation at the end of 10 s pause.
${\displaystyle a}$ ${\displaystyle b=2a}$ ${\displaystyle x}$

The mechanical device shown in abstract form in the diagram opposite - as Eratosthenes calls it - shows two parallel rays and they symbolize two rulers. There are three right-angled triangles between the rulers, the first is fixed at the point, the other two are slidable. Alternatively, three rectangles with drawn diagonals are also possible. The vertically drawn triangles have the variable as height and a small leg of freely selectable length (in the diagram ). The length of the second variable is plotted as a line on the line that is too vertical , at the point of the third triangle . A beam (not shown) from the point through cuts into the line , creates the path and thus reveals the basic idea of ​​the device, namely the theorem of rays . ${\displaystyle s_{1}}$ ${\displaystyle s_{2};}$ ${\displaystyle E,}$ ${\displaystyle E}$ ${\displaystyle b=2a={\overline {AE}}}$ ${\displaystyle 1{,}5a}$ ${\displaystyle s_{1}}$ ${\displaystyle {\overline {HQ}}}$ ${\displaystyle H}$ ${\displaystyle a}$ ${\displaystyle {\overline {HD}}}$ ${\displaystyle A}$ ${\displaystyle D}$ ${\displaystyle K}$ ${\displaystyle s_{1}}$ ${\displaystyle {\overline {AK}}}$

method

Only a few steps are required, e.g. B move the second triangle (blue) and the third triangle (yellow) between the rulers in the following way until the two middle proportions and are found (see animation): ${\displaystyle x}$ ${\displaystyle y}$

Always move the second triangle (blue) towards the point first so that its hypotenuse , the line (red) and the vertical line intersect at the point . Only in the next step push the third triangle (yellow) in such a way that its hypotenuse , the line (red) and the perpendicular intersect at the point . Repetitions of these steps produce the two middle proportions and ${\displaystyle E}$ ${\displaystyle {\overline {GM'}}}$ ${\displaystyle {\overline {AK}}}$ ${\displaystyle {\overline {FM}}}$ ${\displaystyle B}$ ${\displaystyle {\overline {HN'}}}$ ${\displaystyle {\overline {AK}}}$ ${\displaystyle {\overline {FM}}}$ ${\displaystyle C}$ ${\displaystyle x={\overline {FB}}}$ ${\displaystyle y={\overline {GC}}.}$

proof

If the two beams by , or by in is cut, then ${\displaystyle {\overline {AD}}}$ ${\displaystyle {\overline {EH}}}$ ${\displaystyle K}$

Doubling the cube according to Eratosthenes (schematic diagram), proof

${\displaystyle {\overline {EK}}:{\overline {KF}}={\overline {AK}}:{\overline {KB}}={\overline {FK}}:{\overline {KG}}}$

and

${\displaystyle {\overline {EK}}:{\overline {KF}}={\overline {AE}}:{\overline {BF}}}$,

while

${\displaystyle {\overline {FK}}:{\overline {KG}}={\overline {BF}}:{\overline {CG}};}$

therefore

${\displaystyle {\overline {AE}}:{\overline {BF}}={\overline {BF}}:{\overline {CG}}.}$

Similar

${\displaystyle {\overline {BF}}:{\overline {CG}}={\overline {CG}}:{\overline {DH}}.}$

Thus, and are in continuous proportion as well as and the two middle proportions. ${\displaystyle {\overline {AE}},\;{\overline {BF}},\;{\overline {CG}}}$ ${\displaystyle {\overline {DH}}}$ ${\displaystyle {\overline {BF}}}$ ${\displaystyle {\overline {CG}}}$

Construction using special curves

If a cube having an edge length with respect to its volume with doubled as an edge length of the larger cube, the following applies for the determination of the two middle-proportional and of Hippocrates the set of Chios: ${\displaystyle a}$ ${\displaystyle a^{3}}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle y}$

${\displaystyle a:x=x:y=y:2a}$

If one eliminates , the result is: ${\displaystyle y}$

${\displaystyle x^{3}=2a^{3},}$

it follows:

(1)  ${\displaystyle x=a\cdot {\sqrt[{3}]{2}}.}$

If one eliminates , the result is: ${\displaystyle x}$

${\displaystyle y={\frac {2a^{2}}{a\cdot {\sqrt[{3}]{2}}}},}$

it follows:

(2)  ${\displaystyle y={\frac {2a}{\sqrt[{3}]{2}}}.}$

Due to the special degree of difficulty - three-dimensionality, first half of the 4th century BC BC - the solution to the problem with the help of the curve of Archytas is described in detail below.

Curve of Archytas

Situation: The two middle proportions have been found.
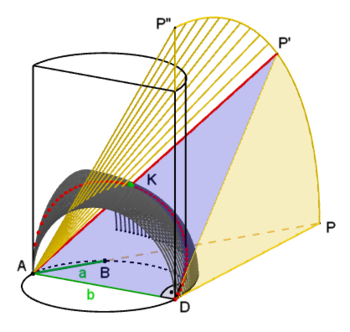
This is characterized by the intersection (green) of the two penetration curves, which are created by the interplay of the three figures: half-cylinder with the curve of Archytas (dotted red), eighth of a rotational torus (anthracite) and conical section (yellow) with a triangular cut surface (blue). diameter ${\displaystyle K}$ ${\displaystyle DPP'A}$ ${\displaystyle b=2a.}$

A few decades earlier than Archytas, Hippocrates of Chios succeeded in doubling the cube by tracing it back to a problem of the construction of proportions. Archytas of Taranto succeeded in their theoretical construction with a special curve named after him. The following three figures are required for their visualization or application (see adjacent diagram):

• Half cylinder , stands on a half circle with radius and diameter The height of the half cylinder is approx. ${\displaystyle ADB}$ ${\displaystyle a}$ ${\displaystyle b.}$ ${\displaystyle 2{,}5a.}$
• Eighth of a so-called rotation torus without a "hole" with a radius ${\displaystyle a.}$
• Section of the cone, taken from the cone with radius and height , with the triangle as its intersection. The cone section reaches its maximum size, namely a quarter of the total cone, when the triangle encloses an angle of with the triangle and thus lies on the rectangular surface of the half-cylinder. ${\displaystyle DPP'A}$ ${\displaystyle r={\overline {DP}}}$ ${\displaystyle h={\overline {DA}}}$ ${\displaystyle DP'A}$ ${\displaystyle DP'A}$ ${\displaystyle DPA}$ ${\displaystyle 90^{\circ }}$

The curve of Archytas is a so-called intersection curve that arises when a half cylinder penetrates one eighth of a rotational torus without a “hole”. As can be seen in the diagram, the quarter of the cone penetrates the two neighboring figures and thus creates a second intersection curve that intersects with the curve of Archytas. ${\displaystyle DPP''A}$

The two middle proportions are found when the hypotenuse of the triangular (blue) section of the cone intersects the curve of Archytas in the (green) point . The point lies on the surface of the half-cylinder (on the curve of Archytas), on the triangular cut surface of the conical section and on the semi-circular cut surface of the rotational torus without a “hole”. ${\displaystyle {\overline {AP'}}}$ ${\displaystyle K}$ ${\displaystyle K}$

Geometric consideration

Geometric considerations regarding the two middle proportions (red) and (blue) ${\displaystyle x}$ ${\displaystyle y}$

The adjacent picture and the similar picture in the following section show the geometric approach that Archytas used to describe the curve he found with the help of two mean proportions . The figure consists of, among other things. of two right-angled , similar triangles and each with a Thales circle . The semicircle standing perpendicular to the base of the semicylinder and rotatable around point - with the two middle proportions and - has the diameter of the diameter of the semicylinder (see picture curve of Archytas) ${\displaystyle AD'K}$ ${\displaystyle AIM}$ ${\displaystyle A}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle {\overline {AD'}},}$ ${\displaystyle {\overline {AD}}.}$

With inserted values ​​from (1) and (2) the following applies according to Hippocrates of Chios:

(3)  ${\displaystyle {\overline {AM}}={\overline {AB}}=a;\;\;{\overline {AD}}={\overline {AD'}}=b}$

(4)  ${\displaystyle {\overline {AI}}=x;\;\;{\overline {AK}}=y}$

The following route conditions apply:

(5)  ${\displaystyle {\overline {AD'}}:{\overline {AM}}=b:a=2:1}$

(6)  ${\displaystyle {\overline {AD'}}:{\overline {AK}}={\overline {AI}}:{\overline {AM}}={\overline {AK}}:{\overline {AI}}=y:x={\sqrt[{3}]{2}}}$

Construction of the edge length of the doubled cube

Cube doubling with part of the curve of Archytas (red);
For the sake of clarity, the torus of rotation is shown in the Curve of Archytas section. Once reached in the animation , this corresponds to the geometric approach of Archytas shown in the small sketch. Animation, between 15 s and at the end 25 s break. See animation of construction ${\displaystyle {\overline {AI}}={\sqrt[{3}]{2}}}$

${\displaystyle \Rightarrow }$

For a graphic representation - as in the adjacent picture - dynamic geometry software (DGS) is required .

It starts with drawing the unit circle with diameter . The subsequent radius to cut the circle in it follow a tangent through and the enlargement both intersect at point A parallel to off cuts the diameter in and the circle in ${\displaystyle {\overline {AD}}=b=2}$ ${\displaystyle a=1}$ ${\displaystyle A}$ ${\displaystyle B.}$ ${\displaystyle D}$ ${\displaystyle {\overline {AB}};}$ ${\displaystyle P.}$ ${\displaystyle {\overline {DP}}}$ ${\displaystyle B}$ ${\displaystyle {\overline {AD}}}$ ${\displaystyle E}$ ${\displaystyle Z.}$

Next, a short circular arc is drawn around with the radius and the point is defined with a freely selectable position. After connecting the point with , this results in the intersection points on and on the semicircle.This is followed by a semicircle above and a vertical line in it results in the intersection point on the semicircle above The next semicircle above and a vertical line in in result in the intersection point on the semicircle via Das This is followed by erecting the half-cylinder (height approx. 2.5) above the semicircle . ${\displaystyle A}$ ${\displaystyle {\overline {AD}}}$ ${\displaystyle D'}$ ${\displaystyle A}$ ${\displaystyle D'}$ ${\displaystyle T}$ ${\displaystyle {\overline {BZ}}}$ ${\displaystyle I}$ ${\displaystyle ADB.}$ ${\displaystyle {\overline {AD'}}}$ ${\displaystyle {\overline {AD'}}}$ ${\displaystyle I,}$ ${\displaystyle K}$ ${\displaystyle {\overline {AD'.}}}$ ${\displaystyle {\overline {BZ}}}$ ${\displaystyle {\overline {BZ}}}$ ${\displaystyle T}$ ${\displaystyle M}$ ${\displaystyle {\overline {BZ}}.}$ ${\displaystyle ADB}$

It continues by drawing an arc around the point with the radius it cuts into the extension of the edge of the half-cylinder that leads to. Now the point is connected with. A line drawn from through the point to the arc results in the intersection point. The connection with creates the triangle that is congruent with the triangle. This is possible because the semicircle above and the quarter circle are parallel to each other. Looking at the context, the two also congruent triangles and and the arc around as the area is a cone with its total amount to be recognized. After connecting the points with and with , the two relevant right-angled triangles and finally result ${\displaystyle D}$ ${\displaystyle {\overline {DP}};}$ ${\displaystyle P''}$ ${\displaystyle D}$ ${\displaystyle P''}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle M}$ ${\displaystyle DPP''}$ ${\displaystyle P'.}$ ${\displaystyle P'}$ ${\displaystyle D}$ ${\displaystyle ADP}$ ${\displaystyle ADP'.}$ ${\displaystyle {\overline {BZ}}}$ ${\displaystyle DPP''}$ ${\displaystyle ADP}$ ${\displaystyle ADP''}$ ${\displaystyle DPP''}$ ${\displaystyle D,}$ ${\displaystyle {\overline {DA}}}$ ${\displaystyle M}$ ${\displaystyle I}$ ${\displaystyle K}$ ${\displaystyle D'}$ ${\displaystyle TIM}$ ${\displaystyle ID'K.}$

The semicircle - the cut surface of a not shown Rotationstorus no "hole" - is to the point now be rotated anti-clockwise until the hypotenuse of also, but clockwise rotated triangle the semicircle in cuts. It should be noted that the lines and are perpendicular to each other. According to Euclid's theorem of heights, this results in ${\displaystyle {\overline {AD'}}}$ ${\displaystyle A}$ ${\displaystyle {\overline {AP'}}}$ ${\displaystyle ADP'}$ ${\displaystyle {\overline {AD'}}}$ ${\displaystyle K}$ ${\displaystyle {\overline {MT}}}$ ${\displaystyle {\overline {BZ}}}$

${\displaystyle {\overline {MT}}^{2}={\overline {ZT}}\cdot {\overline {TB}}={\overline {AT}}\cdot {\overline {TI}}.}$

It follows that the angle is the same in this position . The four triangles , and and are therefore similar to each other. The distance adjusted in this way corresponds to the sought-after edge length of the doubled cube, see above. ${\displaystyle {\overline {MT}}^{2}={\overline {AT}}\cdot {\overline {TI}}}$ ${\displaystyle \angle {AMI}}$ ${\displaystyle 90^{\circ }}$ ${\displaystyle AKD'}$ ${\displaystyle TIM}$ ${\displaystyle ATM}$ ${\displaystyle AIM}$ ${\displaystyle {\overline {AI}}}$ ${\displaystyle x={\sqrt[{3}]{2}}}$

During the rotation of the semicircle, the point in the triangle determines the (red) curve of Archytas on the surface of the semicylinder. ${\displaystyle K}$ ${\displaystyle AD'K}$ ${\displaystyle {\overline {AD'}}}$

• For an exact breakpoint (point meets the hypotenuse of the triangle ) of the animated rotation of the semicircle over the distance is determined with the help of the dynamic geometry software GeoGebra . ${\displaystyle K}$ ${\displaystyle {\overline {AP'}}}$ ${\displaystyle ADP'}$ ${\displaystyle {\overline {AD'}}}$ ${\displaystyle {\overline {AI}}={\sqrt[{3}]{2}}}$

With the help of parabolas

Menaichmos: The point of intersection of the two parabolas provides the two middle proportions and thus also and  and  ${\displaystyle F}$ ${\displaystyle {\overline {FD}}}$ ${\displaystyle {\overline {BD}},}$
${\displaystyle x:a=y:x=b:y={\sqrt[{3}]{2}}}$
${\displaystyle -2p\cdot (-1)=2p=b}$ ${\displaystyle -2q\cdot (-1)=2q=a.}$

Menaichmos solved the problem of constructing the two required mean proportions as the intersection of two conic sections (based on Hippocrates' transformation of the problem).

Johann Christoph Sturm writes about this :

" Dissolution.

  So now there are two straight lines AB and BC, between which two mean
equally behaving olls are found / ſo ſet the two given angles at
right angles to each other / and extend the ſng towards D and E, without measure / beyond; Then describe ſo / as required by
the line BC, umb BE a parabola / (alſo including / that the crossing is a /
line drawn perpendicularly from its perimeter to BE / line (as here the crossing EF) equal to Rechteey the rectangle
from BC and bem part the middle line between B and the previous vertical line (here BE),
add the note below : Again, describe / previous measure / umb BD,
if line AB is required, another parabola / and from point F, in which they
intersect / pull through each other the vertical lines FD and FE, ſo, BE and BD become the coveted
two middle, equally behaving ſeyn . "

- Johann Christoph Sturm : Sturm 1670, p. 119

Iterative approximation construction of the cube root ${\displaystyle {\sqrt[{3}]{2}}}$

For reasons already described above, the result of the cube root cannot be exactly represented with a compass and ruler with finite construction steps. ${\displaystyle 2}$

The Newton method provides a way for very good approximations . In the following it is used to represent the real zero of the function for doubling the cube

${\displaystyle f(x)=x^{3}-2}$

as an approximation to achieve with a few iteration steps.

Can be used as a starting value . The iteration steps of the algorithm are through ${\displaystyle x_{0}=1}$

${\displaystyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}=x_{n}-{\frac {x_{n}^{3}-2}{3\ x_{n}^{2}}}={\frac {2\ x_{n}^{3}+2}{3\ x_{n}^{2}}}}$

Are defined.

Because the expression only contains the basic arithmetic operations , the result of each iteration step can be constructed as a segment with a compass and ruler . ${\displaystyle x_{n+1}}$

Calculation of the iteration steps

In the formula

${\displaystyle x_{n+1}={\frac {2\ x_{n}^{3}+2}{3\ x_{n}^{2}}}}$

the term on the right-hand side of the equation gives the result of the tenth iteration step. An iteration step is made up of six algebraic operations , of which the fifth is always the numerator and the second is the denominator of an improper fraction . ${\displaystyle n-}$

${\displaystyle x_{n}^{2},\ 3\ x_{n}^{2},\ x_{n}^{3},\ 2\ x_{n}^{3},\ 2\ x_{n}^{3}+2\;\Rightarrow \;\;{\frac {2\ x_{n}^{3}+2}{3\ x_{n}^{2}}}=x_{n+1}}$

1st iteration step , five operations have e.g. B. used value for ${\displaystyle x_{1}}$ ${\displaystyle n=0,}$ ${\displaystyle x_{0}^{2},}$ ${\displaystyle x_{n}=x_{0}=1}$

${\displaystyle x_{0}^{2}=1,\ 3\ x_{0}^{2}=3,\ x_{0}^{3}=1,\ 2\ x_{0}^{3}=2,\ 2\ x_{0}^{3}+2=4\;\;\Rightarrow }$

${\displaystyle x_{1}={\frac {2\ x_{0}^{3}+2}{3\ x_{0}^{2}}}={\frac {4}{3}}}$

2nd iteration step , five operations have e.g. B. used value for ${\displaystyle x_{2}}$ ${\displaystyle n=1,}$ ${\displaystyle x_{1}^{2},}$ ${\displaystyle x_{n}=x_{1}={\frac {4}{3}}}$

${\displaystyle x_{1}^{2}={\tfrac {16}{9}},\ 3\ x_{1}^{2}={\tfrac {16}{3}},\ x_{1}^{3}={\tfrac {64}{27}},\ 2\ x_{1}^{3}={\tfrac {128}{27}},\ 2\ x_{1}^{3}+2={\tfrac {182}{27}}\;\;\Rightarrow }$

${\displaystyle x_{2}={\frac {2\ x_{1}^{3}+2}{3\ x_{1}^{2}}}={\tfrac {\tfrac {182}{27}}{\tfrac {16}{3}}}}$

3rd iteration step , five operations have e.g. B. used value for ${\displaystyle x_{3}}$ ${\displaystyle n=2,}$ ${\displaystyle x_{2}^{2},}$ ${\displaystyle x_{n}=x_{2}={\frac {91}{72}}}$

${\displaystyle x_{3}={\frac {2\ x_{2}^{3}+2}{3\ x_{2}^{2}}}={\frac {1126819}{894348}}=1{,}2599334934\ldots }$

This process can be repeated as often as you like. There is a quadratic convergence speed, which makes the method comparatively efficient.

Construction with compass and ruler

After just two iteration steps, the efficiency of the application of the Newton method is clearly recognizable; the approximate value reached up to that point is now followed by a constructive continuation until the third iteration step is reached with the approximate value . ${\displaystyle x_{2}=1{,}263{\overline {8}}.}$ ${\displaystyle x_{3}}$

First, the improper fraction is reformulated into the ( improper ) decimal fraction and then mapped as the exact length on a number line (Fig. 1). This is z. B. the method construction of a decimal number using the 3rd ray theorem . Because of the proportions, it is advantageous to show this in your own picture. ${\displaystyle {\tfrac {91}{72}}}$ ${\displaystyle {\tfrac {9{,}1}{7{,}2}}}$ ${\displaystyle x_{2}}$

In the next step, the length (red) from picture 1 is transferred to picture 2 (green, number 2). This is followed by the determination of the square number (number 3) and the cube number (number 4) of In the fifth step, the cube number of is multiplied by the factor and the number is added. Finally (number 6) the quotient (red) is determined: ${\displaystyle x_{2}}$ ${\displaystyle x_{2}.}$ ${\displaystyle x_{2}}$ ${\displaystyle 2}$ ${\displaystyle 2}$ ${\displaystyle x_{3}}$

${\displaystyle x_{3}={\frac {2\ x_{2}^{3}+2}{3\ x_{2}^{2}}}={\frac {1126819}{894348}}=1{,}259933493\ldots }$

Fig. 1
Construction of the 3rd iteration step, operation 1: break ${\displaystyle x_{2}={\tfrac {9,1}{7,2}}}$

Figure 2
Construction of the 3rd iteration step, operations 2–6 deliver ${\displaystyle x_{3}={\tfrac {1126819}{894348}}}$

Example to illustrate the error

${\displaystyle {\begin{alignedat}{2}{\text{konstruierte Länge }}\qquad x_{3}&=&&1{,}259933\dots \\-{\text{Sollwert }}\qquad -{\sqrt[{3}]{2}}&=-&&1{,}259921\dots \\\hline {\text{absoluter Fehler }}\qquad F&=&&0{,}000012\dots \;[\mathrm {LE} ]\end{alignedat}}}$

In the case of an initial  cube with the edge length m, the edge of the only approximately doubled cube would be approx.  Mm too long. ${\displaystyle 100}$ ${\displaystyle 1{,}2}$

In music theory

In music theory , a natural analog of doubling is the jump of a tone by an octave , i.e. the musical interval that is created by doubling the frequency of the tone. A natural analog of a cube (with volume 2) is the division of the octave into three parts, each with the same interval - this stands for the three equal sides of the cube. In this sense, the problem of doubling the cube is solved by the major third in equal tuning . This is a musical interval that is exactly one third of an octave. It multiplies the frequency of a tone by , i.e. by exactly the length of the side of the doubled cube. ${\displaystyle ({\sqrt[{12}]{2}})^{4}={\sqrt[{3}]{2}}}$

The picture on the side shows the major major third CE. The ratio of the frequencies of the two tones (E: C) corresponds exactly . ${\displaystyle {\sqrt[{3}]{2}}}$

literature

• Arthur Donald Steele: On the role of compasses and ruler in Greek mathematics . In: Sources and studies on the history of mathematics. Department B, Volume 3, 1936, pp. 287-369 ( digitized version ).
• Claas Lattmann: Mathematical modeling in Plato between Thales and Euclid (= Science, Technology, and Medicine in Ancient Cultures. Volume 9). Walter de Gruyter, Berlin / Boston 2019, pp. 177–270 ( limited preview in Google book search).
• Markus Asper: Mathematics. In: Bernhard Zimmermann , Antonios Rengakos (Hrsg.): Handbook of the Greek literature of antiquity. Volume 2: The literature of the classical and Hellenistic period (= Handbook of Classical Studies . Volume 7.2). CHBeck, Munich 2014, pp. 459–481 ( limited preview in Google book search).
• Jesper Lützen: Why was Wantzel overlooked for a century? The changing importance of an impossibility result . In: Historia Mathematica 36, 2009, pp. 374-394 ( online ).

Web links

Wikibooks: Doubling the Cube  - Learning and Teaching Materials

 Wikisource: Delisches Problem  - Article of the 4th edition of Meyers Konversations-Lexikon

• Doubling the cube, McTutor

Individual evidence

1. ↑ See as an English translation with commentary: Reviel Netz : The works of Archimedes. Translated into English, together with Eutocius' commentaries, with commentary, and critical edition of the diagrams . Volume 1: The Two Books On the Sphere and the Cylinder . Cambridge University Press, Cambridge 2004, ISBN 0-521-66160-9 , here pp. 272-306.
2. ↑ On the authenticity of the text of the letter written by Eutokios, WR Knorr: The Ancient Tradition of Geometric Problems. Boston 1986, pp. 17-24. On the question of which king Ptolemy is meant, see, for example, WR Knorr: Textual Studies in Ancient and Medieval Geometry. Boston 1989, pp. 144 f.
3. ↑ ^{a b c} Reviel Netz: The works of Archimedes. Translated into English, together with Eutocius' commentaries, with commentary, and critical edition of the diagrams . Volume 1: The Two Books On the Sphere and the Cylinder . Cambridge University Press, Cambridge 2004, ISBN 0-521-66160-9 , p. 294
4. ^ Richard Kannicht , Bruno Snell : Tragicorum Graecorum Fragmenta . Volume 2, 2nd edition, Vandenhoeck & Ruprecht, Göttingen 2007, p. 62, fragment Adespota F 166; for the treatment of the Glaukos material in the tragedy poets see Georg Weicker : Glaukos 23. In: Paulys Realencyclopädie der classischen Altertumswwissenschaft (RE). Volume VII, 1, Stuttgart 1910, Col. 1415 f.
5. ↑ Claas Lattmann: Mathematical Modeling in Plato between Thales and Euclid (= Science, Technology, and Medicine in Ancient Cultures. Volume 9) provides a detailed analysis of the ancient source material on the Delier anecdote and the possible historical bases . De Gruyter, Berlin / Boston 2019, pp. 187-206; on the three mechanical approaches and Plato's criticism, ibid., pp. 220–241.
6. ^ Reviel Netz: The works of Archimedes. Translated into English, together with Eutocius' commentaries, with commentary, and critical edition of the diagrams . Volume 1: The Two Books On the Sphere and the Cylinder . Cambridge University Press, Cambridge 2004, ISBN 0-521-66160-9 , p. 273, note 17.
7. ↑ For example Joseph: The crest of the peacock. Princeton UP, 2001, p. 330.
8. ↑ ^{a b c d e} Horst Hischer : Moritz Cantor and the crooked line of Archytas of Taranto. (PDF) Saarland University, 2003, p. 74 , accessed on December 2, 2020 . 
9. ↑ ^{a b c} Claas Lattmann: Mathematical modeling in Plato between Thales and Euclid . 5.3 Plato's cube doubling and the mechanical proof (=  Science, Technology, and Medicine in Ancient Cultures . Volume 9 ). Walter de Gruyter GmbH, Berlin / Boston 2019, ISBN 978-3-11-061382-7 , p. 215 ff . ( limited preview in Google Book search).
10. ↑ François Lasserre (ed.): The fragments of Eudoxus by Knidos , Berlin 1966, pp. 20-22, 163-166.
11. ^ Reviel Netz: The works of Archimedes. Translated into English, together with Eutocius' commentaries, with commentary, and critical edition of the diagrams . Volume 1: The Two Books On the Sphere and the Cylinder . Cambridge University Press, Cambridge 2004, ISBN 0-521-66160-9 , p. 295
12. ↑ Hermann Schmdt: Selected higher curves. University of Mainz, March 1949, accessed on December 20, 2020 . 
13. ^ AD Steele: On the role of compasses and ruler in Greek mathematics. In: Sources and studies on the history of mathematics, astronomy and physics. Volume B 3, 1936, pp. 287-369 (also specifically on the problem of cube doubling).
14. ^ Pierre Wantzel: Recherches sur les moyens de reconnaître si un Problème de Géométrie peut se résoudre avec la règle et le compas (=  Journal de mathématiques pures et appliquées (Liouville's Journal) . Volume 2 ). 1837, p. 366-372 .
15. ^ Adhémar Jean Claude Barré de Saint-Venant : Biography Wantzel. Journal des mathématiques pures (Liouville). Nouvelles Annales de Mathématiques, 1848, p. 329 , accessed on December 29, 2020 (French). 
16. ↑ Jesper Lützen: Why was Wantzel overlooked for a century? The changing importance of an impossibility result , Historia Mathematica 36, ​​2009, pp. 378–379.
17. ↑ Jesper Lützen: Why was Wantzel overlooked for a century? The changing importance of an impossibility result , Historia Mathematica 36, ​​2009, p. 379.
18. ↑ Jesper Lützen: Why was Wantzel overlooked for a century? The changing importance of an impossibility result , Historia Mathematica 36, ​​2009, p. 391.
19. ↑ Jesper Lützen: Why was Wantzel overlooked for a century? The changing importance of an impossibility result , Historia Mathematica 36, ​​2009, p. 387.
20. ↑ Christoph J. Scriba, Peter Schreiber: 5000 years of geometry , Springer-Verlag, Third Edition, 2010, p. 405.
21. ↑ Falko Lorenz: Algebra Volume I: Fields and Galois Theory , Springer, pp. 6-13.
22. ^ ^{A b} Claas Lattmann: Mathematical modeling in Plato between Thales and Euclid . 5.3 Plato's cube doubling and the mechanical proof (=  Science, Technology, and Medicine in Ancient Cultures . Volume 9 ). Walter de Gruyter GmbH, Berlin / Boston 2019, ISBN 978-3-11-061382-7 , p. 213 ( limited preview in Google Book search).
23. ↑ Klaus Volkert: History of geometric construction problems I. (PDF) In: Lecture, University of Cologne in the winter semester 06/07; [...] heptagon. University of Wuppertal, 2006, p. 20 , accessed on September 15, 2018 . 
24. ^ Heinrich Dörrie : 35. The Delian Cube-doubling Problem. In: 100 Great Problems of Elementary Mathematics. New York, Dover Publications, Inc., 1965, pp. 170-171 , accessed May 5, 2019 . 
25. ^ Skip Lester: History of Mathematics. (PDF) 7. Isaac Newton (1642-1727) suggested the following construction for duplicating the cube. University of Washington, p. 11 , accessed November 8, 2019 . 
26. ↑ ^{a b c} Horst Hischer: Moritz Cantor and the crooked line of Archytas of Taranto. (PDF) Saarland University, 2003, p. 76 , accessed on October 30, 2020 . 
27. ^ Claas Lattmann: Mathematical modeling in Plato between Thales and Euclid . 5.23 The archaeological and historical perspective (=  Science, Technology, and Medicine in Ancient Cultures . Volume 9 ). Walter de Gruyter GmbH, Berlin / Boston 2019, ISBN 978-3-11-061382-7 , p. 199–212 ( limited preview in Google Book search).
28. ↑ Claas Lattmann: Mathematical Modeling in Plato between Thales and Euclid, 5 Plato and the Delic Problem, 5.2.4 Conclusion , Walter de Gruyter, Berlin / Boston 2019, p. 207 ( limited preview in the Google book search)
29. ^ Rudolf Haller (translator): Euclid: Elements Stoicheia . Book 1, Proposition 29 . Edition Opera-Platonis, Markgröningen 2017.
30. ^ Rudolf Haller (translator): Euclid: Elements Stoicheia . Book 1, Proposition 32 . Edition Opera-Platonis, Markgröningen 2017.
31. ^ Rudolf Haller (translator): Euclid: Elements Stoicheia . Book 6, Proposition 4 . Edition Opera-Platonis, Markgröningen 2017.
32. ^ Translation according to Claas Lattmann: Mathematical modeling in Plato between Thales and Euclid. Walter de Gruyter, Berlin / Boston 2019, p. 182, ISBN 978-3-11-061382-7 , ( limited preview in Google book search).
33. ^ Reviel Netz: The Works of Archimedes . Eutocius' Commentary To On The Sphere And The Cylinder II, As Eratosthenes. Ed .: Cambridge University Press. University Press, New York 2004, ISBN 978-0-521-66160-7 , pp. 294–298 (English, google.de [accessed December 10, 2020]).
34. ↑ Bartel Leendert van der Waerden : Science Awakening. 1956, 230 f. Three rectangles or triangles that could be moved along a ruler, one side of which could be freely rotated.
35. ^ ^{A b} Thomas Heath: A History of Greek Mathematics . The Duplication Of The Cube, (ζ) Eratosthenes. Ed .: Internet Archive. tape 1 . The Clarendon Press, Oxford 1921, pp. 259 (English).
36. ↑ ^{a b} Horst Hischer: Moritz Cantor and the crooked line of Archytas of Taranto. (PDF) Saarland University, 2003, p. 79 ff. , Accessed on November 1, 2020 . 
37. ↑ Rudolf Stopfer: The doubling of the cube, 5th solution according to Archytas. Seminar: Classical Problems of Antiquity. University of Bayreuth, June 8, 1997, accessed October 30, 2020 . 
38. ↑ Horst Hischer: 6.1 Solution: Intersection of two parables according to Menaichmos. (PDF) On the problem of doubling the cube in the illustration by Johann Christoph Sturm 1670. Saarland University, 2015, pp. 9–10 , accessed on May 1, 2019 . 
39. ↑ Johann Christoph Sturm: The second artificial or geometrical way… . In: The Incomparable ARCHJMEDJS Kunſt books. 1670. DTA German Text Archive, p. 118 ff., Accessed on November 2, 2020.
40. ↑ man: Elementary Algebra Aein. Docuri, July 10, 2016, pp. 61–63 , accessed on December 16, 2020 (English). 
41. ^ Paul Bamberg: Differentiability, Newton's method, inverse functions. canvas.harvard, July 7, 2016, p. 31 , accessed December 16, 2020 . 
42. ^ RC Phillips: The equal tempered scale , Musical Opinion and Music Trade Review, 29 (337): 41-42, 1905.

This article was added to the list of excellent articles on December 30, 2020 in this version .