Quadratrix des Hippias

Quadratrix (red); Snapshot for F and E at six tenths of their way

The Quadratrix or Trisektrix des Hippias (also Quadratrix des Dinostratos ) is a kinematically generated curve , the invention of which is attributed to the tradition after the Greek sophist Hippias von Elis (5th century BC). It is one of the oldest examples of a kinematically generated curve and was used to solve two of the three great ancient geometrical problems , the trisection of the angle and the squaring of the circle . Hippias used them around 420 BC. To the three-parting of the angle (hence Trisektrix ) and Dinostratos around 350 BC. To square the circle (hence quadratrix ).

definition

Quadratrix as a flat curve ( a = 1)

Quadratic rix as a function ( a = 1)

In the square ABCD a quarter circle around A is drawn with the side length of the square as the radius. A point E traverses the quarter circle from D to B with constant angular velocity. Also at constant speed, F traverses the route DA , in such a way that E and F start at D at the same time and arrive at B and A at the same time . The quadratrix then results as a locus of the intersection point S of the route AE with the parallels to AB by F .

If you place the above square with a given side length a in a (Cartesian) coordinate system that side AB is on the x -axis and point A is at the origin, then the quadrix is ​​described by a flat curve and the following applies: ${\displaystyle \gamma :(0,{\tfrac {\pi }{2}}]\rightarrow \mathbb {R} ^{2}}$

${\displaystyle \gamma (t)={\begin{pmatrix}x(t)\\y(t)\end{pmatrix}}={\begin{pmatrix}{\frac {2a}{\pi }}t\cot(t)\\{\frac {2a}{\pi }}t\end{pmatrix}}}$

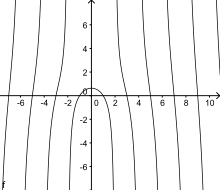
This representation can now also be used to define the quadrix outside of its associated square, although it is not defined at the definition gaps. It can, however, be continuously continued in the formal definition gap at due . This gives a steady curve on the interval . ${\displaystyle \cot(t)}$ ${\displaystyle t=0}$ ${\displaystyle \lim _{t\to 0}t\cot(t)=1}$ ${\displaystyle (-\pi ,\pi )}$

If you want to describe the quadratrix as a (easily representable) function, it is useful to swap the x and y axes, that is, you put AB on the y axis instead of on the x axis. Then the quadratrix is ​​described by the following function f (x) :

${\displaystyle f(x)=x\cdot \cot \left({\frac {\pi }{2a}}\cdot x\right)}$

Angular division

Quadratrix compasses

Tripartite an angle

It is not possible to divide any angle into three with a compass and ruler. However, if you allow the use of a quadratrix as an additional aid, i.e. if you assume that a quadratrix can be drawn over an angle limb, then it is possible to subdivide any angle into n equal angles. This also makes it possible to divide an angle into three ( n  = 3). For a square with a fixed length, a Quadratrix can be drawn with the help of a Quadratrix compass or a Quadratrix template.

Since, according to the definition of the quadratrix, the traversed angle is proportional to the traversed route section on the square side, a division of this route section into n equal parts also provides a division of the associated angle into n equal parts. The division of any route into n parts is possible due to the theorem of rays with a compass and ruler.

At a given angle BAE (≤ 90 °) one first builds a square ABCD over its leg AB and draws the corresponding square rix. The second leg of the angle intersects the quadratrix at a point G , and the straight line through G parallel to the leg AB intersects the side of the square AD in F ; then AF is the route section proportional to the angle BAE . Now it carries on one of A outgoing beam n equidistant points and connects the last point O with F . The straight lines parallel to OF are drawn through the equidistant points; their intersections with the segment AF then provide the division of this segment into n equal parts. The parallels to the side of the square AB through these intersection points intersect the square rix. The points of intersection on the quadratrix then divide the angle BAE into n equal parts.

With compasses and ruler alone you cannot create every point of the quadratrix, but only a dense subset . With this you can approximate a quadratrix as well as you want, but an exact angle division without a device for generating a quadratrix is ​​generally not possible, since the required quadratrix points do not have to be in this subset that can be constructed with the help of compasses and ruler.

Squaring the circle

Quadrature the quarter circle with r = 1

It is impossible to square the circle with a compass and ruler alone. If, however, one allows Hippias's quadratrix as an additional aid, then the Dinostratos theorem enables a square to be constructed with a compass and ruler with the same area as a quarter circle. The double-sided square then has the same area as the full circle.

The theorem of Dinostratos says that the quadratic rix of Hippias divides the side of the corresponding square in proportion . For a given quadrant with radius r one first constructs the corresponding circumscribed square ABCD with side length r . Then the quadratrix of this square intersects the square side AB in J and it applies . Now one sets up a segment JK in J , which is perpendicular to AB and has the length r . Then meets the line AK , the extended side BC in L . According to the ray theorem applies . If the square side AB is extended beyond B by the distance , then BL and BO form the base of a rectangle OBLN , the area of ​​which corresponds to that of the quarter circle. A square of equal area can be constructed for this rectangle with the help of Euclid's theorem of heights and Thales's theorem (see also the quadrature of the rectangle ). To do this, extend the side of the rectangle ON by the line , create a semicircle with NQ as the diameter and extend the line AO so that it intersects the semicircle in R. According to Thales' theorem, the triangle NQR is right-angled, and according to Euclid's theorem of heights, its height OR is the base of a square, which is equal in area to the rectangle OBLN and thus also to a quarter circle. ${\displaystyle {\tfrac {2}{\pi }}}$ ${\displaystyle \left|{\overline {AJ}}\right|={\tfrac {2}{\pi }}r}$ ${\displaystyle \left|{\overline {BL}}\right|={\tfrac {\pi }{2}}r}$ ${\displaystyle \left|{\overline {BO}}\right|={\tfrac {r}{2}}}$ ${\displaystyle \left|{\overline {OQ}}\right|={\tfrac {r}{2}}}$

The point of intersection J of the quadratrix with the side of the square AB is, however, not defined when applying the geometric definition, since the two lines to be cut coincide at this point and there is no clear intersection. This means that point J can not be constructed "exactly" with a compass and ruler or with the help of the above Quadratrix compass.

Historical

In historical sources the Quadratrix is ​​mentioned in Proklos (412–485), Pappos (3rd / 4th century) and Iamblichos (approx. 240–325). Proclus states Hippias as the discoverer of a curve called quadratrix and describes elsewhere how Hippias uses this curve to divide any angle into three. Pappos, on the other hand, describes how a curve called a quadratrix was used by Dinostratos, Nicomedes, and others to square the circle. However, he does not mention Hippias by name, nor does he explicitly name someone who discovered the curve. Iamblichus only states in a short sentence that Nicomedes used a curve known as quadratrix to square the circle.

Although it is conceivable, due to the name of the curve as quadratrix in Proklos, that Hippias also used the curve himself for quadrature, this source situation is usually interpreted by mathematicians to mean that Hippias discovered the curve, but only used it to divide the angle into three and its application to quadrature goes back to later mathematicians, especially Dinostratos and Nicomedes. This reading of the historical sources goes back to Moritz Cantor .

literature

• Hans-Wolfgang Henn: Elementary Geometry and Algebra . Verlag Vieweg + Teubner, 2003, pp. 45–48 Squaring the circle ( excerpt (Google) )
• Felix Klein : Famous Problems of Elementary Geometry . Cosimo 2007 (reprint), ISBN 978-1-60206-417-1 , pp. 57–58 ( excerpt (Google) )
• Audun Holme: Geometry: Our Cultural Heritage . Springer 2010, ISBN 978-3-642-14440-0 , pp. 114–116 ( excerpt (Google) )
• Thomas Little Heath : A History of Greek Mathematics. Volume 1. From Thales to Euclid . Clarendon Press 1921 (reprinted by Elibron Classics 2006), pp. 225–230 ( archive.org )
• Horst Hischer: Classical problems of antiquity - examples of "historical anchoring" . (PDF; 539 kB). In: Jürgen Blankenagel, Wolfgang Spiegel (Ed.): Mathematics didactics out of enthusiasm for mathematics - Festschrift for Harald Scheid . Klett, Stuttgart / Düsseldorf / Leipzig 2000, pp. 97–118.
• Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics . MAA 2010, ISBN 978-0-88385-348-1 , pp. 146-147 ( excerpt (Google) )

Web links

Commons : Quadratrix of Hippias  - Collection of images, videos and audio files

• Quadratrix and the squaring of the circle. University of Lüneburg
• Michael D. Huberty, Ko Hayashi, Chia Vang: Hippias' Quadratrix
• Eric W. Weisstein : Quadratrix of Hippias . In: MathWorld (English).
• John J. O'Connor, Edmund F. Robertson :  Quadratrix of Hippias. In: MacTutor History of Mathematics archive .
• Suzanne Harper, Shannon Driskell: An Investigation of Historical Geometric Constructions . In: Convergence , August 2010

Individual evidence

1. ↑ ^{a b c} Horst Hischer: Classical Problems of Antiquity - Examples of “Historical Anchoring” (PDF; 539 kB). In: Jürgen Blankenagel, Wolfgang Spiegel (Ed.): Mathematics didactics out of enthusiasm for mathematics - Festschrift for Harald Scheid . Klett, Stuttgart / Düsseldorf / Leipzig 2000, pp. 97–118.
2. ^ ^{A b c} Hans-Wolfgang Henn: Elementary geometry and algebra . Verlag Vieweg + Teubner 2003, pp. 45–48 Squaring the circle ( excerpt (Google) )
3. ^ ^{A b} Hans Niels Jahnke: A History of Analysis . American Mathematical Society 2003, ISBN 0-8218-2623-9 , pp. 30–31 ( excerpt (Google) )
4. ↑ Eric W. Weisstein : Quadratrix of Hippias . In: MathWorld (English).
5. ^ ^{A b} Dudley Underwood: The Trisectors . Cambridge University Press 1994, ISBN 0-88385-514-3 , pp. 6–8 ( excerpt (Google) )
6. ^ John J. O'Connor, Edmund F. Robertson :  Quadratrix of Hippias. In: MacTutor History of Mathematics archive .
7. ↑ Audun Holme: Geometry: Our Cultural Heritage . Springer 2010, ISBN 978-3-642-14440-0 , pp. 114–116 ( excerpt (Google) )
8. ^ Jean-Paul Delahaye : Pi - The Story . Springer 1999, ISBN 3-7643-6056-9 , p. 71 ( excerpt (Google) )
9. ^ John J. O'Connor, Edmund F. Robertson :  Dinostratus. In: MacTutor History of Mathematics archive .
10. ↑ Van der Waerden: Science Awakening . Oxford University Press 1961, p. 146
11. ^ ^{A b} James Gow : A Short History of Greek Mathematics . 1884, Reprint: Cambridge University Press 2010, ISBN 978-1-108-00903-4 , pp. 162-164 ( excerpt (Google) )
12. ^ ^{A b} Thomas Little Heath : A History of Greek Mathematics. Volume 1. From Thales to Euclid . Clarendon Press 1921 (reprinted by Elibron Classics 2006), pp. 182, 225-230 ( archive.org ).