Seventeenth corner

Regular seventeenth corner

The seventeen- or Heptadekagon is a geometric figure , to the group of polygons ( polygons belongs). It is defined by seventeen points that are connected by seventeen lines to form a closed line .

In the following, this article deals with the regular seventeen corner , which is convex , has seventeen sides of equal length and whose corners lie on a common perimeter , as well as the regular overturned seventeenth corner .

properties

The special thing about a regular seventeenth-corner is the fact that it can be constructed - it can therefore be drawn using only compasses and rulers (the Euclidean tools ) - but this constructibility has not been proven for thousands of years. The proof only succeeded Carl Friedrich Gauß in the year 1796. He showed that for the cosine of the central angle

${\displaystyle \cos {\frac {360^{\circ }}{17}}={\frac {1}{16}}\left(-1+{\sqrt {17}}+{\sqrt {2\left(17-{\sqrt {17}}\right)}}+2{\sqrt {17+3{\sqrt {17}}-{\sqrt {2\left(17-{\sqrt {17}}\right)}}-2{\sqrt {2\left(17+{\sqrt {17}}\right)}}}}\right)\qquad \approx 0{,}93247222940435580457311589182156}$

applies, from which the constructibility results. It can also be used to calculate various sizes of the seventeenth-corner such as side length, circumference, incircle radius, diagonal over two sides and area.

On June 21, 1801, Gauss presented the above formula to the St. Petersburg Academy in a so-called short version in three steps, which results from the grouping of sums of individual cosine values. Friedrich L. Bauer describes them in detail in 2009 in his book Historical Notes on Computer Science in the chapter Carl Friedrich Gauß, das 17-Eck and MATHEMATIKA , so only the result of the short version is mentioned here.

With the auxiliary variables and ${\displaystyle q}$ ${\displaystyle q'}$

${\displaystyle q=\cos {\frac {2\pi }{17}}+\cos 4\cdot {\frac {2\pi }{17}}}$ and

${\displaystyle q'=\cos 3\cdot {\frac {2\pi }{17}}+\cos 5\cdot {\frac {2\pi }{17}},}$

thus also applies to the cosine of the central angle

${\displaystyle \cos \left({\frac {2\pi }{17}}\right)={\frac {1}{2}}q+{\sqrt {{\frac {1}{4}}q^{2}-{\frac {1}{2}}q'}}}$ such as

${\displaystyle \cos \left({\frac {2\pi }{17}}\right)={\frac {1}{2}}\cdot \left(q+{\sqrt {\left(qq-2q'\right)}}\;\right)}$

Sizes of a regular seventeenth corner with the circumferential radius , the central angle and its cosine ${\displaystyle r_{\rm {u}}}$ ${\displaystyle \textstyle \mu ={\tfrac {360^{\circ }}{17}}}$ ${\displaystyle \textstyle \epsilon =\cos \mu }$

Side length	${\displaystyle s={\sqrt {2\left(1-\epsilon \right)}}\cdot r_{\rm {u}}}$	${\displaystyle \approx 0{,}367499\cdot r_{\rm {u}}}$
scope	${\displaystyle U=17{\sqrt {2\left(1-\epsilon \right)}}\cdot r_{\rm {u}}}$	${\displaystyle \approx 6{,}247484\cdot r_{\rm {u}}}$
Inscribed radius	${\displaystyle r_{\rm {i}}={\sqrt {\frac {1+\epsilon }{2}}}\cdot r_{\rm {u}}}$	${\displaystyle \approx 0{,}982973\cdot r_{\rm {u}}}$
Diagonal across two sides	${\displaystyle d_{2}=2{\sqrt {1-\epsilon ^{2}}}\cdot r_{\rm {u}}}$	${\displaystyle \approx 0{,}722483\cdot r_{\rm {u}}}$
Area	${\displaystyle A={\frac {17}{2}}{\sqrt {1-\epsilon ^{2}}}\cdot r_{\rm {u}}^{2}}$	${\displaystyle \approx 3{,}070554\cdot r_{\rm {u}}^{2}}$
Interior angle	${\displaystyle \phi =180^{\circ }-\mu ={\frac {15}{17}}\cdot 180^{\circ }}$	${\displaystyle \approx 158{,}823529^{\circ }}$

Math background

Announcement of the constructibility in the intelligence sheet of the general literature newspaper (1796)

Gauss's discovery is based on a solution of the equation of division of a circle , the solutions of which - the seventeenth roots of unity  - form a regular seventeenth-octagon with radius 1 in the Gaussian plane of complex numbers . This equation can be solved solely by using nested square roots (see above for the real part of the solution that is counterclockwise closest to solution 1). In 1796, when he was 18 years old, Gauß recognized this possibility "through intense reflection ... in the morning ... (before I got out of bed)" due to general number-theoretic properties of prime numbers, in this case specifically the prime number 17: the modulo of a prime number , from 0 different remainder classes can be represented as powers of a so-called primitive root, in which case one can specifically choose: ${\displaystyle x^{17}-1=0}$ ${\displaystyle \cos(2\pi /17)}$ ${\displaystyle \zeta =e^{2\pi i/17}}$ ${\displaystyle p}$ ${\displaystyle 1,\ldots ,{p-1}}$ ${\displaystyle g^{0}=1,g^{1}=g,g^{2},\dotsc ,g^{p-2}}$ ${\displaystyle g}$ ${\displaystyle p=17}$ ${\displaystyle g=3}$

${\displaystyle {\begin{aligned}&1,\quad 3\cdot 1=3,\quad 3\cdot 3=9,\quad 3\cdot 9\mod 17=10,\quad 3\cdot 10\mod 17=13,\\&5,\;15,\;11,\;16,\;14,\;8,\;7,\;4,\;12,\;2,\;6\end{aligned}}}$

If you now sort the 17th roots of unity that differ from 1, that is, in the order

${\displaystyle \zeta ,\ \zeta ^{3},\ \zeta ^{9},\ \zeta ^{10},\ \zeta ^{13},\ \zeta ^{5},\ \zeta ^{15},\ \zeta ^{11},\ \zeta ^{16},\ \zeta ^{14},\ \zeta ^{8},\ \zeta ^{7},\ \zeta ^{4},\ \zeta ^{12},\ \zeta ^{2},\ \zeta ^{6},}$

Thus, by partial summation of every second, every fourth or every eighth root of unit from this list, one obtains the so-called Gaussian periods : two 8-part periods with 8 summands each, four 4-part periods with 4 summands each and eight 2-part periods with 2 summands each. On the basis of fundamental properties or through explicit calculation, the following can be shown:

• The two 8-term periods are solutions of a quadratic equation with whole coefficients .
• The four 4-part periods are solutions of two quadratic equations, whose coefficients can be calculated from the 8-part periods.
• The eight 2-part periods are solutions of four quadratic equations, the coefficients of which can be calculated from the 4-part periods.

This applies to the two-part period to the “first” root of unity . ${\displaystyle \zeta +\zeta ^{16}=\zeta +\zeta ^{-1}=2\cos(2\pi /17)}$

The approach described can be carried out analogously for every prime number of the form . Five such prime numbers, called “ Fermat's prime numbers ”, are known: 3, 5, 17, 257, 65537. Therefore, the regular 257-corner and the regular 65537-corner belong to the constructable polygons . ${\displaystyle 2^{2^{k}}+1}$

Geometric constructions

Construction using the Gaussian abstract of the formula

On the occasion of the 150th anniversary of the death of Carl Friedrich Gauß on February 23, 2005, the exhibition "How lightning strikes, the riddle has been solved" was held in Göttingen in the old town hall on the market from February 23 to May 15, 2005. Carl Friedrich Gauss in Göttingen. The catalog for this exhibition, edited by Elmar Mittler, contains articles in various categories. In the Mathematics section, you can find article 17 Equal Corners and Edges with Compasses and Ruler by Hans Vollmayr. The construction shown below is basically taken from the chapters The Seventeen: The Calculation and The Seventeen: The Drawing .

The short version of the formula for the cosine of the central angle (see properties ),

${\displaystyle \cos \left({\frac {2\pi }{17}}\right)={\frac {1}{2}}\cdot \left(q+{\sqrt {\left(qq-2q'\right)}}\;\right),}$

facilitates a construction with compass and ruler, which with the help of the auxiliary variables, quasi step by step, supplies the cosine of the central angle. One possible solution is to graphically represent the auxiliary variables separately in three images (1 - 3) with elementary algebraic operations . This makes the construction clear and generally easy to understand.

Construction of the auxiliary quantities p and q as well as the product qq

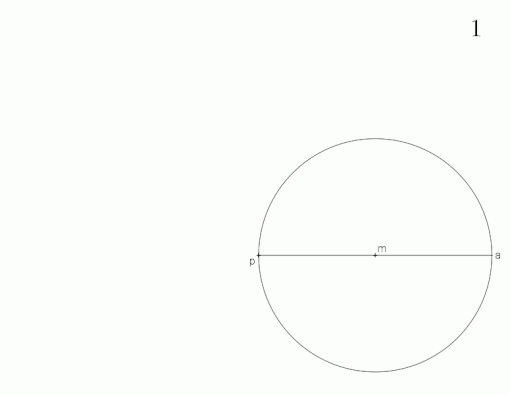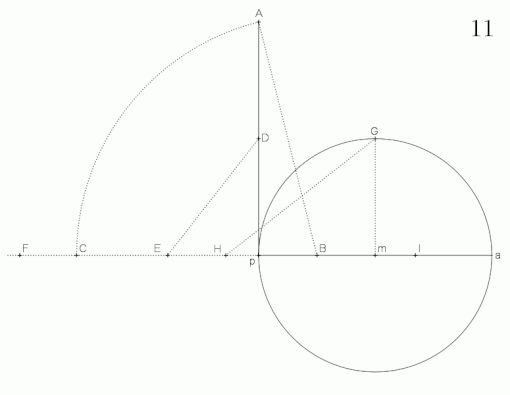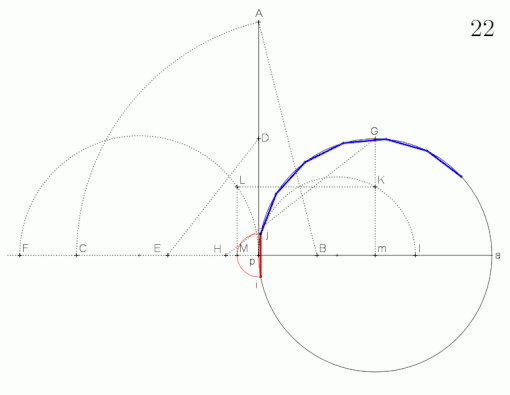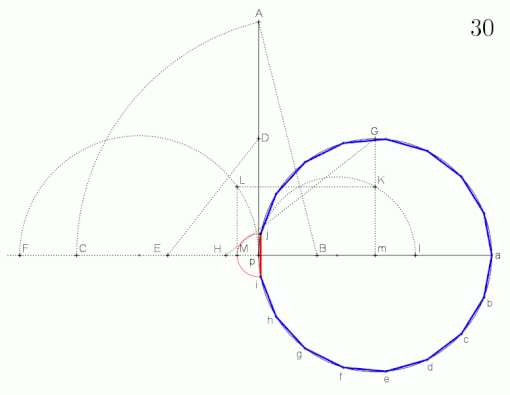
Figure (1): Construction of the auxiliary quantities p and q as well as the product qq

In it applies

${\displaystyle p={\frac {-1+{\sqrt {17}}}{4}}}$

such as

${\displaystyle q={\frac {p+{\sqrt {1+pp}}}{2}}.}$

Image 1)

1. From point one half-line pull out with Lot on track in building and from yields transferred to Lot ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle {\overline {AB}}=1,}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle A}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle A}$ ${\displaystyle C.}$
2. Perpendicular to in with length then results in a half line from through results ${\displaystyle {\overline {AB}}}$ ${\displaystyle B}$ ${\displaystyle ={\frac {1}{4}}\cdot {\overline {AB}}}$ ${\displaystyle D,}$ ${\displaystyle A}$ ${\displaystyle D}$ ${\displaystyle {\overline {AD}}={\frac {1}{4}}\cdot {\sqrt {17}}.}$
3. Circle around through results in a half-line, is an auxiliary variable ${\displaystyle D}$ ${\displaystyle B}$ ${\displaystyle E}$ ${\displaystyle {\overline {AE}}}$ ${\displaystyle p.}$
4. Quarter circle around through results and now with connect, subsequent parallel to ab results and with the product ${\displaystyle A}$ ${\displaystyle E}$ ${\displaystyle F}$ ${\displaystyle G,}$ ${\displaystyle C}$ ${\displaystyle F}$ ${\displaystyle {\overline {CF}}}$ ${\displaystyle G}$ ${\displaystyle H}$ ${\displaystyle {\overline {AH}}}$ ${\displaystyle pp.}$
5. Add the length to twice , results in and then cut in half and draw across a semicircle . ${\displaystyle pp}$ ${\displaystyle =1={\overline {AC}}}$ ${\displaystyle I}$ ${\displaystyle J,}$ ${\displaystyle {\overline {AJ}}}$ ${\displaystyle K}$ ${\displaystyle K}$ ${\displaystyle {\overline {AJ}}}$
6. Plumb up in to semicircle results then add to from auxiliary variable results in ${\displaystyle {\overline {AJ}}}$ ${\displaystyle I}$ ${\displaystyle {\overline {IL}}={\sqrt {\left(pp+1\right)}},}$ ${\displaystyle {\overline {IL}}}$ ${\displaystyle L}$ ${\displaystyle p={\overline {AE}}}$ ${\displaystyle M.}$
7. ${\displaystyle {\overline {IM}}}$cut in half results in an auxiliary size ${\displaystyle N}$ ${\displaystyle {\overline {IN}}=q.}$
8. Quarter circle around from results in quarter circle around from results in ${\displaystyle I}$ ${\displaystyle J}$ ${\displaystyle O,}$ ${\displaystyle I}$ ${\displaystyle N}$ ${\displaystyle P.}$
9. ${\displaystyle O}$connect with , subsequent parallel to ab results and with the product ${\displaystyle P}$ ${\displaystyle {\overline {OP}}}$ ${\displaystyle N}$ ${\displaystyle Q}$ ${\displaystyle {\overline {IQ}}}$ ${\displaystyle qq.}$

Construction of the auxiliary quantities p 'and q'

Figure (2): Construction of the auxiliary quantities p 'and q'

In it applies

${\displaystyle p'={\frac {-1-{\sqrt {17}}}{4}}}$

such as

${\displaystyle q'={\frac {p'+{\sqrt {1+p'p'}}}{2}}.}$

Picture 2)

1. From point a ray pull out with solder on track in building and from yields transferred to Lot ${\displaystyle A'}$ ${\displaystyle B'}$ ${\displaystyle {\overline {A'B'}}=1,}$ ${\displaystyle {\overline {A'B'}}}$ ${\displaystyle A'}$ ${\displaystyle {\overline {A'B'}}}$ ${\displaystyle A'}$ ${\displaystyle C'.}$
2. Perpendicular to in with the length then results in a half-line from through results ${\displaystyle {\overline {A'B'}}}$ ${\displaystyle B'}$ ${\displaystyle ={\frac {1}{4}}\cdot {\overline {A'B'}}}$ ${\displaystyle D',}$ ${\displaystyle A'}$ ${\displaystyle D'}$ ${\displaystyle {\overline {A'D'}}={\frac {1}{4}}\cdot {\sqrt {17}}.}$
3. Circle around through results in a half-line, is an auxiliary variable ${\displaystyle D'}$ ${\displaystyle B'}$ ${\displaystyle E'}$ ${\displaystyle {\overline {A'E'}}}$ ${\displaystyle p'.}$
4. Quarter circle around through results and now with connect, subsequent parallel to ab results and with the product ${\displaystyle A'}$ ${\displaystyle E'}$ ${\displaystyle F'}$ ${\displaystyle G',}$ ${\displaystyle C'}$ ${\displaystyle F'}$ ${\displaystyle {\overline {C'F'}}}$ ${\displaystyle G'}$ ${\displaystyle H'}$ ${\displaystyle {\overline {A'H'}}}$ ${\displaystyle p'p'.}$
5. Add the length to twice , results in and then cut in half and draw across a semicircle. ${\displaystyle p'p'}$ ${\displaystyle =1={\overline {A'C'}}}$ ${\displaystyle I'}$ ${\displaystyle J',}$ ${\displaystyle {\overline {A'J'}}}$ ${\displaystyle K'}$ ${\displaystyle K'}$ ${\displaystyle {\overline {A'J'}}}$
6. Plumb up in to semicircle then subtract from from auxiliary variable results in ${\displaystyle {\overline {A'J'}}}$ ${\displaystyle I'}$ ${\displaystyle {\overline {I'L'}}={\sqrt {\left(p'p'+1\right)}},}$ ${\displaystyle {\overline {I'L'}}}$ ${\displaystyle L'}$ ${\displaystyle p'={\overline {A'E'}}}$ ${\displaystyle M'.}$
7. ${\displaystyle {\overline {I'M'}}}$in halving yields with auxiliary quantity ${\displaystyle N'}$ ${\displaystyle {\overline {I'N'}}}$ ${\displaystyle q'.}$

Construction of the root of qq-2q 'and the cosine of the central angle μ

Image (3): Construction of the root of qq-2q 'and the cosine of the central angle μ

Picture 3)

1. Draw a half line from the point , transfer the product from image (1) to it, then result in the length from image (1) transferred from ${\displaystyle I}$ ${\displaystyle qq}$ ${\displaystyle Q,}$ ${\displaystyle =1={\overline {AC}}}$ ${\displaystyle Q}$ ${\displaystyle R.}$
2. Of the length of image (2) from point subtract results then in half and to over tighten semicircle. ${\displaystyle qq}$ ${\displaystyle 2q'={\overline {I'M'}}}$ ${\displaystyle I}$ ${\displaystyle S,}$ ${\displaystyle {\overline {SR}}}$ ${\displaystyle T}$ ${\displaystyle T}$ ${\displaystyle {\overline {SR}}}$
3. Plumb up in until semicircle results ${\displaystyle {\overline {SR}}}$ ${\displaystyle Q}$ ${\displaystyle {\overline {QU}}={\sqrt {\left(qq-2q'\right)}}.}$
4. Stretch draw and to auxiliary quantity from Image (1) from add results then in half, the distance is the cosine of the central angle of the Siebzehnecks. ${\displaystyle {\overline {Q'U'}}={\sqrt {\left(qq-2q'\right)}}}$ ${\displaystyle q={\overline {IN}}}$ ${\displaystyle U'}$ ${\displaystyle V,}$ ${\displaystyle {\overline {Q'V}}}$ ${\displaystyle W}$ ${\displaystyle {\overline {WV}}}$ ${\displaystyle \cos \left({\frac {2\pi }{17}}\right)={\frac {1}{2}}\cdot \left(q+{\sqrt {\left(qq-2q'\right)}}\;\right)}$ ${\displaystyle \mu }$
5. Draw a circle around the point with the radius (e.g. with a line ), then draw in the radius ${\displaystyle W'}$ ${\displaystyle =1}$ ${\displaystyle {\overline {QR}}}$ ${\displaystyle P_{17}.}$
6. ${\displaystyle {\overline {WV}}=\cos \left({\frac {2\pi }{17}}\right)}$transferred up from , results ${\displaystyle {\overline {W'P_{17}}}}$ ${\displaystyle W'}$ ${\displaystyle V'.}$
7. Plumb line on in to circumference results in the first corner point of the resulting seventeenth corner . ${\displaystyle {\overline {W'V'}}}$ ${\displaystyle V'}$ ${\displaystyle P_{1}}$
8. ${\displaystyle {\overline {P_{1}P_{17}}}}$Remove fifteen times counterclockwise on the circumference and finally connect the neighboring corners. The regular seventeenth corner is thus completed.

${\displaystyle \ldots }$

In principle, it would also be possible to represent the (long) expression that Gauss found first as a constructed segment. However, no such solution is described in the relevant literature.

Construction according to Georg Paucker

One of the first geometrical construction instructions for the regular seventeen-sided comes from Magnus Georg Paucker , who presented it to the Kurländische Gesellschaft für Literatur und Kunst in 1819, where it was published in 1822.

Construction sketch after Magnus Georg Paucker		Animation of the sketch

1. On the diameter pa around the center m, draw the circumference of the 17-gon.
2. Establish the diameter pA = pa perpendicular to p.
3. Halve the radius mp in B.
4. Extend pa from p.
5. Plot the distance AB from B onto the extension, the intersection is C.
6. Halve pA in D.
7. Halve pC in E.
8. Plot the distance ED from E on the extension, the intersection is F.
9. Establish the radius mG perpendicular to m.
10. Halve mC in H.
11. Plot the line HG from H to pa , the intersection is I.
12. Construct the semicircle over pF .
13. Construct the semicircle over pI , the intersection with mG is K.
14. Draw the parallel to mP from K, the intersection with the semicircle over pF is L.
15. Drop the perpendicular from L to mH , the base point is M.
16. Draw the circular arc with radius pM up to the circumference, the point of intersection is i.
17. Plot the segment MF from p on the circumference, the point of intersection is c of the chord pc , the circular arc (pca) is the double circular arc of the 17-gon.
18. Halve the angle cpa, the point of intersection is b of the chord pb , so the distance from is the first side of the 17-gon.
19. Plot the distance from ab c five times clockwise on the circumference, the chords pd , pe , pf , pg and ph result .
20. Plot the distance from i eight times clockwise on the circumference.
21. Connect the points found in this way to form a complete 17-gon.

Construction after Herbert Richmond

In 1825, Johannes Erchinger presented a design to the Göttingen Academy of Sciences , which Gauss then discussed in the Göttingen Scholars advertisements . The following simpler construction is from Herbert William Richmond in 1893.

Construction sketch after Herbert William Richmond		Animation of the sketch

If the circumference around the resulting seventeenth-corner with the center O is given, the seventeenth-corner can be constructed by:

1. Draw the diameter through the center  O; The point of intersection with the circumference is A, later also designated as P17.
2. Establishing the radius perpendicular to AO on O up to the perimeter; The point of intersection with the circumference is B.
3. Construction of the point I by quartering the segment BO ; I is closer to O.
4. Construction of point E by quartering the angle OIA.
5. Construction of the point F using a perpendicular on EI on I; Halving the 90 ° angle; The point of intersection with the diameter is F and the angle FIE is 45 °.
6. Construction of the Thaleskreis via AF ; The intersection with BO is K.
7. Draw the semicircle around the center E with the radius  EK ; Points of intersection with the diameter are N ₃ and N ₅ (N _{3 is} very close to the center of the Thales circle above AF ).
8. Establishing the perpendicular to the central axis from N ₃ ; The point of intersection with the circumference is the corner point  P _{3 of} the seventeenth corner ; the circular arc OAP ₃ is thus 3/17 of the circumference.
9. Establishing the perpendicular to the central axis from N ₅ ; The point of intersection with the circumference is the corner point P _{5 of} the seventeenth corner ; the circular arc OAP ₅ is therefore 5/17 of the circumference.
10. A fourteen-fold removal of the line AP ₃ on the circumference, from the corner point P ₃ counterclockwise, results in the corner points P ₆ , P ₉ , P ₁₂ , P ₁₅ , P ₁ , P ₄ , P ₇ , P ₁₀ , P ₁₃ , P ₁₆ , P ₂ , P ₈ , P ₁₁ and P ₁₄ .
11. Connecting the points P ₁ , P ₂ , ..., P ₁₇ , P _{1 found in this way} completes the 17-gon.

Construction according to Duane DeTemple

Duane W. DeTemple published a construction of the seventeenth- corner in the mathematical journal The American Mathematical Monthly in 1991 . For his solution he used u. a. four so-called Carlyle circles .

Construction sketch after Duane W. DeTemple		Animation of the sketch, at the end 20 s pause

Play media file

Video

1. Draw the x-axis and put the point on it ${\textstyle 0=(0\;;\;0).}$
2. Draw intersections with are and around the unit circle with radius ${\displaystyle O}$ ${\displaystyle c_{1}}$ ${\displaystyle r_{1},}$ ${\displaystyle c_{1}}$ ${\displaystyle P_{0}=(+r_{1}\;;\;0)}$ ${\displaystyle Q=(-r_{1}\;;\;0).}$
3. Construct the y-axis from the periphery of the resulting 17-gon, intersection with is ${\displaystyle c_{1}}$ ${\displaystyle c_{1}}$ ${\displaystyle A=(0\;;\;r).}$
4. Halve the radius in ${\displaystyle {\overline {OQ}}}$ ${\textstyle Q'=\left({\frac {-r}{2}}\;;\;0\right).}$
5. Pull the circular arc having the radius to ${\displaystyle c_{2}}$ ${\displaystyle r_{2}={\overline {Q'P_{0}}}}$ ${\textstyle \left(r_{2}={\frac {3}{2}}\cdot r_{1}\right)}$ ${\displaystyle Q'.}$
6. Create a vertical line on the radius from the intersection with is ${\displaystyle {\overline {OQ}}}$ ${\displaystyle Q',}$ ${\displaystyle c_{2}}$ ${\textstyle M_{0}=\left({\frac {-r_{1}}{2}}\;;\;-1{,}5\;r_{1}\right).}$
7. Pull the Carlyle-circular arc around by (with ) so as to be the x-axis by the radius meets twice, points of intersection are and ${\displaystyle Cc_{1}}$ ${\displaystyle M_{0}}$ ${\displaystyle A}$ ${\textstyle r_{Cc1}={\frac {1}{2}}{\sqrt {26}}\cdot r_{1}}$ ${\displaystyle c_{1}}$ ${\textstyle H_{0,2}=\left({\frac {1}{2}}\left(-1+{\sqrt {17}}\right)\cdot r_{1}\;;\;0\right)}$ ${\textstyle H_{1,2}=\left({\frac {1}{2}}\left(-1-{\sqrt {17}}\right)\cdot r_{1}\;;\;0\right).}$
8. Halve the distance in ${\displaystyle {\overline {OH_{0,2}}}}$ ${\textstyle M_{0,2}=\left({\frac {1}{4}}\left(-1+{\sqrt {17}}\right)\cdot r_{1}\;;\;0\right).}$
9. Halve the distance in ${\displaystyle {\overline {OH_{1,2}}}}$ ${\textstyle M_{1,2}=\left({\frac {1}{4}}\left(-1-{\sqrt {17}}\right)\cdot r_{1}\;;\;0\right).}$
10. Drag the Carlyle arc to starting up on the x-axis intercept is ${\displaystyle Cc_{2}}$ ${\displaystyle M_{1,2}}$ ${\displaystyle A}$ ${\textstyle H_{1,4}=\left({\frac {r_{1}}{4}}\left({\sqrt {34+2{\sqrt {17}}}}-{\sqrt {17}}-1\right)\;;\;0\right).}$
11. Drag the Carlyle arc to starting up on the x-axis intercept is ${\displaystyle Cc_{3}}$ ${\displaystyle M_{0,2}}$ ${\displaystyle A}$ ${\textstyle H_{0,4}=\left({\frac {r_{1}}{4}}\left({\sqrt {34-2{\sqrt {17}}}}+{\sqrt {17}}-1\right)\;;\;0\right).}$
12. Plot from the point on the straight line . You get point ${\displaystyle {\overline {OH_{1,4}}}}$ ${\displaystyle A}$ ${\displaystyle {\overline {OA}}}$ ${\textstyle Y=\left(0\;;\;{\frac {r_{1}}{4}}\left({\sqrt {34+2{\sqrt {17}}}}-{\sqrt {17}}+3\right)\right).}$
13. Connect with ${\displaystyle Y}$ ${\displaystyle H_{0,4}.}$
14. Halve the distance in ${\displaystyle {\overline {H_{0,4}Y}}}$ ${\textstyle M_{0,4}=\left({\frac {r_{1}}{8}}\left({\sqrt {34-2{\sqrt {17}}}}+{\sqrt {17}}-1\right)\;;\;{\frac {r_{1}}{8}}\left({\sqrt {34+2{\sqrt {17}}}}-{\sqrt {17}}+3\right)\right).}$
15. Drag the Carlyle arc to starting up on the x-axis intercept is ${\displaystyle Cc_{4}}$ ${\displaystyle M_{0,4}}$ ${\displaystyle A}$ ${\displaystyle H_{0,8}.}$
16. Draw the arc with the radius around the intersection points with the perimeter are the corner points and thus the line is the first side of the 17-gon you're looking for. ${\displaystyle c_{3}}$ ${\displaystyle {\overline {OP_{0}}}}$ ${\displaystyle H_{0,8},}$ ${\displaystyle c_{1}}$ ${\displaystyle P_{1}}$ ${\displaystyle P_{16},}$ ${\displaystyle {\overline {P_{0}P_{1}}}}$
17. A fourteen-times removal of the route on the circumference from the corner point counterclockwise, results in the corner points up to ${\displaystyle {\overline {P_{0}P_{1}}}}$ ${\displaystyle c_{1},}$ ${\displaystyle P_{1}}$ ${\displaystyle P_{2}}$ ${\displaystyle P_{16}.}$
18. Connect the points found in this way and then the 17-sided is completely drawn. ${\displaystyle P_{1},}$ ${\displaystyle P_{2}\ldots ,}$ ${\displaystyle P_{16}}$ ${\displaystyle P_{0},}$

Occurrence

Rose window, Mädlerpassage in Leipzig

In the Leipziger Mädlerpassage a rose window is embedded in the dome of the rotunda , the outline of which resembles a seventeenth corner. It measures about twelve meters in diameter and is approximately fifteen meters high. The rose window was built by the architect Theodor Kösser as part of his Mädlerpassage project (1912–1914).

Regular overturned seventeen corner

A regular, overturned seventeen corner is obtained when at least one is skipped over each time when connecting the seventeen corner points and the tendons thus created are of equal length. Such regular stars are noted with Schläfli symbols , indicating the number of corner points and connecting every -th point. ${\displaystyle \left\{n/k\right\}}$ ${\displaystyle n}$ ${\displaystyle k}$

The following gallery shows the seven possible regular seventeen-ray stars, also called heptadecagrams.

• Regular seventeen ray stars
• 

  ${\displaystyle \left\{17/2\right\}{,}\ \left\{17/15\right\}}$

• 

  ${\displaystyle \left\{17/3\right\}{,}\ \left\{17/14\right\}}$

• 

  ${\displaystyle \left\{17/4\right\}{,}\ \left\{17/13\right\}}$

• 

  ${\displaystyle \left\{17/5\right\}{,}\ \left\{17/12\right\}}$

• 

  ${\displaystyle \left\{17/6\right\}{,}\ \left\{17/11\right\}}$

• 

  ${\displaystyle \left\{17/7\right\}{,}\ \left\{17/10\right\}}$

• 

  ${\displaystyle \left\{17/8\right\}{,}\ \left\{17/9\right\}}$

See also

• Division of circles
• Seventeenth corner, construction from 1818

literature

• Godfrey Harold Hardy , EM Wright : An Introduction to the Theory of Numbers . Oxford University Press, 2008, ISBN 978-0-19-921986-5 , Chapter 5.8: Construction of the regular polygon of 17 sides , p. 71-77 .
• Harold Scott MacDonald Coxeter : Introduction to Geometry . 2nd Edition. Wiley, 1989, ISBN 0-471-50458-0 , pp. 26-28 .
• Karin Reich : The discovery and early reception of the constructibility of the regular 17-sided and its geometric construction by Johannes Erchinger (1825) . In: Rüdiger Thiele (Ed.): Mathesis, Festschrift for the seventieth birthday of Matthias Schramm . GNT-Verlag, Berlin / Diepholz 2000, p. 101-118 .

Individual evidence

1. ↑ H. Maser: Die Teilung des Kreises ..., Article 365. In: Carl Friedrich Gauss' investigations into higher arithmetic . Published by Julius Springer, Berlin 1889; Göttingen Digitization Center, University of Göttingen, p. 446 ff , accessed on March 15, 2018 . 
2. ^ Friedrich L. Bauer: Historical Notes on Computer Science . Ed .: Springer-Verlag. Berlin, Heidelberg 2009, pp. 413 ( Google Books, Carl Friedrich Gauß, das 17-Eck and MATHEMATIKA, The Method of Grouping [accessed on July 20, 2018]).
3. ↑ Hans Vollmayr: 17 equal corners and edges with compasses and ruler . In: Göttinger Bibliotheksschriften 30 “As lightning strikes, the riddle has been solved” Carl Friedrich Gauß in Göttingen. Ed .: Elmar Mittler. Lower Saxony State and University Library, Göttingen 2005, ISBN 3-930457-72-5 , p. 103 ( The seventeenth corner: the drawing, → "... so that at the end we only have the equation ..." [PDF; accessed on January 23, 2020]).
4. ↑ Quoted from Jörg Bewersdorff : Algebra for beginners: From equation resolution to Galois theory , Springer Spectrum, 6th edition 2019, ISBN 978-3-658-26151-1 , p. 90, doi: 10.1007 / 978-3-658 -26152-8_7 .
5. ↑ For details see Bewersdorff, pp. 92–96.
6. ↑ Hans Vollmayr: 17 equal corners and edges with compasses and ruler . In: Göttinger Bibliotheksschriften 30 “As lightning strikes, the riddle has been solved” Carl Friedrich Gauß in Göttingen. Ed .: Elmar Mittler. Lower Saxony State and University Library, Göttingen 2005, ISBN 3-930457-72-5 , p. 90 ff . ( 17 equal corners and edges with compasses and ruler [PDF; accessed on January 23, 2020]).
7. ↑ Hans Vollmayr: 17 equal corners and edges with compasses and ruler . In: Göttinger Bibliotheksschriften 30 “As lightning strikes, the riddle has been solved” Carl Friedrich Gauß in Göttingen. Ed .: Elmar Mittler. Lower Saxony State and University Library, Göttingen 2005, ISBN 3-930457-72-5 , p. 100–102 ( The seventeenth corner: the bill [PDF; accessed on January 23, 2020]).
8. ↑ Hans Vollmayr: 17 equal corners and edges with compasses and ruler . In: Göttinger Bibliotheksschriften 30 “As lightning strikes, the riddle has been solved” Carl Friedrich Gauß in Göttingen. Ed .: Elmar Mittler. Lower Saxony State and University Library, Göttingen 2005, ISBN 3-930457-72-5 , p. 102-103 . ( The seventeenth corner: the drawing [PDF; accessed January 15, 2019]).
9. ↑ Magnus Georg Paucker: Geometric distortion of the regular seventeen-corner and two hundred and fifty-seven corner in the circle . In: Annual Negotiations of the Courland Society for Literature and Art . tape 2 , 1822, p. 160-219 ( introduction , description, pp. 187-188 and illustration after p. 416 (Fig. 12) ).
10. ↑ Carl Friedrich Gauß: Göttingische learned advertisements . tape 87 , no. 203 , December 19, 1825, p. 2025–2027 ( books.google.de ).
11. ^ Herbert W. Richmond: A Construction for a regular polygon of seventeen sides . In: The Quarterly Journal of Pure and Applied Mathematics . tape 26 , 1893, pp. 206-207 ( description and illustration (Fig. 6)]).
12. ↑ Duane W. Detemple: Carlyle Circles and the Lemoine Simplicity of Polygon Constructions. ( Memento of August 11, 2011 in the Internet Archive ). The American Mathematical Monthly, Vol. 98, No. 2 (Feb., 1991), pp. 101-104 ( JSTOR 2323939 ) accessed April 3, 2017.
13. ↑ Anke beesch: Mädlerpassage in Leipzig. In: Architecture Historical architecture in the middle of Leipzig. Retrieved November 3, 2018 . 

Web links

Wikibooks: Siebzehneck  - learning and teaching materials

Commons : Regular seventeenth-corner  collection of images, videos, and audio files

Wiktionary: Seventeenth corner  - explanations of meanings, word origins, synonyms, translations

Wiktionary: heptadecagram  - explanations of meanings, word origins , synonyms, translations

• Eric W. Weisstein : Heptadecagon . In: MathWorld (English).
• Edmund Weitz : The regular 17-sided. In: YouTube. 2017, accessed August 27, 2020 .