Interior angle

Interior angles α, β, γ of a triangle

The interior angles of a polygon are geometrically the angles which are enclosed by two neighboring polygon sides and which lie inside the polygon. The corners of the polygon form the vertices of the interior angles. Each corner has exactly interior angles. In a polygon that is not overturned , the sum of the interior angles only depends on the number of corners of the polygon. A secondary angle of an interior angle, which is created by extending a polygon side, is called an exterior angle . ${\ displaystyle n}$ ${\ displaystyle n}$

Designations

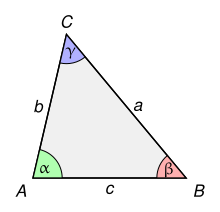
If the corners of a polygon are marked with , the interior angles are usually mentioned . The corner is the vertex of the angle , the corner is the vertex of the angle, and so on. In the case of a triangle , the side opposite the angle is designated with , the side opposite the angle with and so on (see illustration). ${\ displaystyle A, B, C, \ ldots}$ ${\ displaystyle \ alpha, \ beta, \ gamma, \ ldots}$ ${\ displaystyle A}$ ${\ displaystyle \ alpha}$ ${\ displaystyle B}$ ${\ displaystyle \ beta}$ ${\ displaystyle \ alpha}$ ${\ displaystyle a}$ ${\ displaystyle \ beta}$ ${\ displaystyle b}$

Special cases

A non-convex pentagon with an interior angle greater than 180 °

If all interior angles in a triangle are smaller than , it is said to be acute ; measures one of the interior angles precisely , at right angles ; and if one of the interior angles is greater than , obtuse-angled . With an isosceles triangle , two of the three interior angles are the same size. ${\ displaystyle 90 ^ {\ circ}}$ ${\ displaystyle 90 ^ {\ circ}}$ ${\ displaystyle 90 ^ {\ circ}}$

If two opposing interior angles are the same size in a square , a parallelogram is present; two adjacent interior angles are the same size, an isosceles trapezoid . With a chordal quadrilateral, two opposing interior angles complement each other . ${\ displaystyle 180 ^ {\ circ}}$

With an equiangular polygon , all interior angles are the same size. Important examples of equiangular polygons are the regular polygons , for example the equilateral triangle , the square or the regular pentagon , in which all sides are also of the same length.

In a convex polygon , all interior angles measure at most . In the case of a non-convex polygon, there is at least one re-entrant corner with an interior angle greater than . ${\ displaystyle 180 ^ {\ circ}}$ ${\ displaystyle 180 ^ {\ circ}}$

Two polygons are not necessarily similar to each other if all of the corresponding interior angles match. For example, rectangles with different aspect ratios are not similar to each other.

properties

Angle sum

In a triangle, the sum of the interior angles is always α + β + γ = 180 °. The two blue and red angles are step or alternating angles on parallel straight lines and are therefore the same size.

The sum of the interior angles of not over battered -Ecks results in Euclidean geometry always ${\ displaystyle n}$

{\ displaystyle \ alpha + \ beta + \ gamma + \ dotsb = (n-2) \ cdot 180 ^ {\ circ}}

.

In a triangle the sum of the interior angles is therefore always , in a square it is always and in a pentagon it is always . In an equiangular (and therefore especially also in a regular) polygon with corners, all interior angles result to ${\ displaystyle 180 ^ {\ circ}}$ ${\ displaystyle 360 ^ {\ circ}}$ ${\ displaystyle 540 ^ {\ circ}}$ ${\ displaystyle n}$

{\ displaystyle \ alpha = \ beta = \ gamma = \ dotsb = {\ frac {n-2} {n}} \ cdot 180 ^ {\ circ}}

.

Therefore all interior angles measure in an equilateral triangle , in a square and in a regular pentagon . However, these statements no longer apply in non-Euclidean geometries . In an elliptical geometry , for example on a spherical surface , the internal angle sum is always greater than in Euclidean geometry, in a hyperbolic geometry , for example on a saddle surface , it is always smaller. ${\ displaystyle 60 ^ {\ circ}}$ ${\ displaystyle 90 ^ {\ circ}}$ ${\ displaystyle 108 ^ {\ circ}}$

Bisector

Triangle with inside angle bisector (red), outside angle bisector (green), inscribed circle (blue) and circles (orange)

The bisectors of the interior angles of a tangent polygon , for example a triangle or a diamond , meet in the inscribed center of the polygon.

In a triangle, each interior bisector divides the opposite side in relation to the two adjacent sides. It also cuts the bisector of the two non-adjacent outer angles in the center of the circle on the opposite side.

Mathematical sentences

Relationships between the interior angles and the sides of a triangle are established, among other things, by the law of sines , the law of cosines , the law of tangents , the half-angle theorems and Mollweid's formulas .

According to the law of external angles , every external angle of a triangle is equal to the sum of the two non-adjacent internal angles. According to Morley's theorem, the Morley triangle , which is created by dividing the three interior angles of a triangle into thirds, is always equilateral.

In equiangular polygons, Viviani's theorem applies , according to which the sum of the distances from any point inside the polygon to the sides of the polygon is independent of the position of the point.

literature

Arnfried Kemnitz: Mathematics at the beginning of the course . Springer, 2014, ISBN 978-3-658-02081-1 .
Ilka Agricola , Thomas Friedrich : Elementary Geometry . Springer, 2010, ISBN 978-3-8348-9826-5 .

Individual evidence

^ Arnfried Kemnitz: Mathematics at the beginning of the course . Springer, 2014, p. 131-132 .

Web links

Wiktionary: Innenwinkel - explanations of meanings, word origins, synonyms, translations

[1] Arnfried Kemnitz: Mathematics at the beginning of the course . Springer, 2014, p. 131-132 .