Hyperbolic geometry

The hyperbolic geometry (also called Lobachevskian geometry or Lobachevsky geometry ) is an example of a non-Euclidean geometry that is obtained if one adds the contradicting hyperbolic axiom to the axioms of absolute geometry instead of the axiom of parallels that characterizes the Euclidean geometries . This means that for a straight line g and a point P (which does not lie on g ) there is not just one, as in Euclidean geometry, but at least two straight lines ( h and i ) that go through P and are parallel to g . The fact that two straight lines are "parallel" to one another only means that they lie in the same plane and have no points in common, not that they have the same distance everywhere ( h and i only have one point P in common ).
It can be shown that for any straight line g through any point outside of g there are infinitely many non- intersecting lines (“parallels”) that lie in the plane defined by the point and the line. Two of them are in a borderline position and are called border- parallel (also: horoparallel) to the straight line, while the remaining straight lines are called superparallel (also: hyperparallel).
Representations of the real hyperbolic plane
There are several ways in which the real hyperbolic plane can be represented in the real Euclidean plane. Most of these can be generalized to higher dimensions.
In each of these ways, the same abstract hyperbolic geometry is represented: the real hyperbolic plane. It is therefore possible to convert between these representations and statements in purely hyperbolic geometry are independent of the "model" used. Usually one speaks of different models in mathematics if two non-isomorphic structures satisfy the same system of axioms. In this respect, the following “models” describe the same structure, so they are just different representations of a model. However, these representations are always referred to as models in the literature, and this is also the case here. For hyperbolic planes over other bodies and more than two-dimensional hyperbolic spaces, see Metric absolute geometry .
Circular disk model from Beltrami and Klein
In this representation developed by Eugenio Beltrami and Felix Klein , the following applies:
- The hyperbolic plane is modeled by an open circular disk.
- Hyperbolic lines are modeled by tendons .
- Lengths are defined by a special distance function (the angles are also different from the Euclidean values).
This representation is also known under the name "beer mat geometry".
Distance function
Are A and B , two points of the circular disk, so that by meets A and B extending chord the circle in two points R and S . The hyperbolic distance between A and B is now defined using the double ratio:
- .
Poincaré circular disk model
The following applies to the circular disk model by Henri Poincaré , which goes back to Beltrami :
- The hyperbolic plane is modeled by an open circular disk (usually the unit circle).
- Hyperbolic straight lines are modeled by arcs (and diameters ) that are perpendicular to the edge.
- The hyperbolic angle measurement corresponds to the Euclidean angle measurement, the angle between two circular arcs being determined via their tangents at the point of intersection.
- The hyperbolic length measurement is carried out using a special distance function.
Distance function
Let A and B be two points on the disk. If the plane is understood as a complex number plane, the points A , B correspond to complex numbers a , b . The hyperbolic distance between A and B is now defined using these complex numbers:
Poincaré half-plane model
In Henri Poincaré's half-plane model, which goes back to Beltrami:
- The hyperbolic plane is modeled by the upper half plane (y> 0).
- Hyperbolic straight lines are modeled by arcs (and half-lines ) that are perpendicular to the x-axis.
- The hyperbolic angle measurement corresponds to the Euclidean angle measurement, the angle between two circular arcs being determined via their tangents at the point of intersection.
Distance function
The distance between two points of the upper half-plane is calculated using the following formula:
Hyperboloid model
The hyperboloid model, which goes back to Poincaré, embeds the hyperbolic plane in the three-dimensional Minkowski space .
Erlangen program
In the sense of Felix Klein's Erlanger program, hyperbolic geometry is the geometry of
- .
The Beltrami-Klein model shows that hyperbolic geometry can be understood as part of projective geometry.
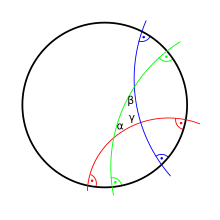
triangle
In real hyperbolic geometry, the sum of the angles in a triangle is always smaller than π (180 degrees; or two rights, if you want to avoid the angle measure). For very large triangles it can be made as small as you want. The area of the triangle is calculated using Johann Heinrich Lambert's formula:
where α , β and γ are the respective angles, Δ is the area and the constant C is a scaling factor. The scaling factor C depends on the system of units used and should basically be set to 1. If the factor C is negative, one speaks of a (positive) Gaussian curvature . Similarly, Thomas Harriot previously defined the formula in 1603
for the area of a triangle on a spherical surface that is formed by circles with the same radius as the sphere. The relationship applies here
- .
Since the hyperbolic geometry requires a positive value for C , R must be due to
be about an imaginary radius.
See also
- Hyperbolic space
- Elliptical geometry
- Nikolai Lobachevsky
- János Bolyai
- Giovanni Girolamo Saccheri and Saccheri-Viereck
literature
- history
- Jeremy Gray: Ideas of Space: Euclidean, Non-Euclidean, and Relativistic . 2nd Edition. Oxford University Press, Oxford 1989, ISBN 0-19-853935-5 .
- Marvin Jay Greenberg: Euclidean & Non-Euclidean Geometries: Development and History. WH Freeman, 1993, ISBN 0-7167-2446-4 .
- David Hilbert : Fundamentals of Geometry . 14th edition. Teubner, Stuttgart / Leipzig 1999, ISBN 3-519-00237-X ( online copy of the 1903 edition [accessed on June 28, 2013]).
- Nikolai I. Lobachevsky: Pangeometry, Edited and translated by Athanase Papadopoulos, Heritage of European Mathematics. Vol. 4, European Mathematical Society (EMS), Zurich, ISBN 978-3-03719-087-6 .
- Hyperbolic geometry in the context of differential geometry (geometries on surfaces)
- Norbert A'Campo, Athanase Papadopoulos: Notes on hyperbolic geometry. In: Strasbourg Master class on Geometry. European Mathematical Society (EMS), Zurich, ISBN 978-3-03719-105-7 , pp. 1–182, doi: 10.4171 / 105 . (IRMA Lectures in Mathematics and Theoretical Physics, Vol. 18)
- Athanase Papadopoulos (Ed.): Handbook of Teichmüller theory. Vol. I, European Mathematical Society (EMS), Zurich 2007, ISBN 978-3-03719-029-6 , doi: 10.4171 / 029 . (IRMA Lectures in Mathematics and Theoretical Physics 11)
- Athanase Papadopoulos (Ed.): Handbook of Teichmüller theory. Vol. II, European Mathematical Society (EMS), Zurich 2009, ISBN 978-3-03719-055-5 , doi: 10.4171 / 055 . (IRMA Lectures in Mathematics and Theoretical Physics 13)
- Athanase Papadopoulos (Ed.): Handbook of Teichmüller theory. Vol. III, European Mathematical Society (EMS), Zurich 2012, ISBN 978-3-03719-103-3 , doi: 10.4171 / 103 . (IRMA Lectures in Mathematics and Theoretical Physics 19)
- The (real) hyperbolic plane as a model of an absolute geometry in the Hilbertian sense
- Friedrich Bachmann : Structure of geometry from the concept of reflection . 2nd supplemented edition. Springer, Berlin / Heidelberg / New York 1973, ISBN 3-540-06136-3 , V: Hyperbolic Geometry and §20.13: Hilbert Planes ( defines absolute geometry in a very general way, explains the peculiarities of real hyperbolic geometry against this background).
- Benno Klotzek: Euclidean and non-Euclidean elementary geometries . 1st edition. Harri Deutsch, Frankfurt am Main 2001, ISBN 3-8171-1583-0 ( elementary does not simply mean here : solving construction tasks and coordinating the “classic” non-Euclidean geometries).
Individual evidence
- ↑ a b Klotzek (2001), 2.1
- ↑ Susanne Müller-Philipp, Hans-Joachim Gorski: Guide to Geometry: For students of teaching posts . Vieweg + Teubner Verlag, 5th expanded edition, 2012, ISBN 978-3-8348-1234-6 , p. 71 ( excerpt (Google) )